基于减载系数变化的风电机组一次调频控制
曾雪洋,张 纯,王顺亮,李小鹏,刘天琪
(1. 国网四川省电力公司电力科学研究院,四川成都 610041;2. 四川大学电气工程学院,四川成都 610065)
0 引言
近年来,以双馈风电机组DFIG(Double-Fed In⁃duction Generator)和永磁直驱风电机组PMSG(Permanent Magnet Synchronous Generator)为主的变速风电机组VSWT(Variable Speed Wind Turbine)在电网中的并网容量不断增加[1⁃2]。与同步发电机不同,VSWT 通过电力电子变频器接入电网,其转速与电网频率解耦,转子的旋转惯量被隐藏。此外,为了捕获最大的风能,VSWT 的输出功率通常由最大功率点跟踪MPPT(Maximum Power Point Tracking)控制,VSWT 不具有功率备用,不能提供类似于同步发电机的一次调频[3⁃4]。随着风电接入比例的不断提高,部分同步发电机将会被VSWT 取代,电力系统的惯量和调频能力将会持续降低,这将给电力系统的频率稳定与控制带来严峻的挑战[5⁃6]。
为此,世界风电大国都明确要求风电提供频率支撑[7⁃9]。国内外学者开展了大量相关研究工作,提出了许多使风电机组利用自身调节能力来参与频率调节的措施,常见的措施有虚拟惯性(无功率备用)和一次调频(有功率备用)。
提供虚拟惯性的风电机组运行在MPPT 运行点,通过控制风电机组的电磁功率或者电磁转矩使其转速临时变化,从而使风电机组在短时间内释放或者吸收转子的旋转动能,用于提供类似于同步发电机惯性响应的虚拟惯性。常见的风电机组提供虚拟惯性支撑的控制方法有虚拟惯性控制、下垂控制以及二者结合的综合惯性控制[10⁃15]。虚拟惯性控制中将频率的微分作为输入信号,用于抑制频率变化率,而下垂控制中将频率的偏差作为输入信号,用于减小最大频率偏差。转子动能提供虚拟惯性的能力与所储备的动能密切相关,如果转速下降到一定值,则风电机组将会退出调频来避免低速脱网,这可能会引起频率二次跌落[16]。此外,利用动能参与频率调节,风电机组会偏离MPPT 运行点(转速会偏离最优转速),无论转速上升还是下降,风电机组捕获的功率都会减少,这会加剧转速恢复过程中的频率跌落[17]。由于没有功率备用,虚拟惯性仅能实现短期调频,改善暂态过程中的频率特性,对于稳态频率无改善作用。
对于大规模风电并网的系统,风电机组提供的虚拟惯性已经不能满足调频需求,还需要使风电机组提供一次调频。为了实现一次调频,事先要对风电机组进行减载控制来预留调频所需的功率备用,减载控制可以通过变桨距角控制和超速控制实现。变桨距角控制通过增加风电机组的桨距角来预留功率备用,通过在变桨距角控制中引入下垂控制来实现一次调频[18]。变桨距角控制可以实现全风速下的减载控制,但是由于有机械部分的参与,该控制的响应速度较慢,且频繁地调节桨距角会加剧风电机组的磨损,缩短风电机组寿命,增加风电机组运行成本[19]。此外,变桨距角控制减少的风能直接被丢弃,风能利用率降低。超速控制是通过提高风电机组运行的转子转速,使风电机组运行在捕获风能曲线最大功率点的右侧,这样在风电机组参与频率调节的过程中出现转速下降时,其捕获的功率会增加,超速控制与下垂控制相结合可实现一次调频。相较于变桨距角控制,超速控制是通过脉冲宽度调制PWM(Pulse Width Modulation)控制实现的,其响应速度较快,部分减载丢弃的风能可以以旋转动能的形式储存,但超速控制不适用于全风速下的控制,在高风速下需要与变桨距角控制相结合。为充分利用2 种减载控制的优势,文献[20⁃21]提出在低风速时采用超速控制而在高风速时采用变桨距角控制的协调控制。但上述协调控制没有考虑超速减载控制的功率跟踪曲线与下垂控制间的交互影响,这种交互影响使传统一次调频控制下风电机组提供的实际附加功率小于下垂控制的附加功率,导致调频过程中不能充分释放减载控制储备的功率,削弱了一次调频控制的效果。
针对上述问题,本文首先分析传统一次调频控制下超速减载控制的功率跟踪曲线与下垂控制间的交互影响机制,然后提出一种消除这种交互影响的基于减载系数变化的一次调频控制,并给出相关控制参数的设置方法,最后在PSCAD/EMTDC 中搭建仿真模型,仿真结果表明,所提一次调频控制的支撑功率与转子转速解耦,仅与频率偏差和下垂系数有关,能够较好地模拟同步发电机一次调频的功率支撑效果,有效消除上述交互影响,调频控制效果优于传统风电机组的一次调频控制。
1 PMSG模型
本文以PMSG 为例进行研究,下文所提控制策略也适用于DFIG。典型的PMSG 模型如附录A 图A1所示,PMSG 通过一台背靠背变流器接入电网,发电机侧变流器控制风电机组发出的功率,风电机组根据运行的转子转速从功率跟踪曲线上获得定功率控制的参考值,电网侧变流器控制直流电压和变流器与电网交换的无功功率。风电机组模型详细介绍参考文献[22]。
将风电机组从空气中捕获的功率Pwind作为输入风电机组发电机的机械功率。根据空气动力学原理,Pwind为:

式中:ρ为空气密度;R为风电机组叶片半径;vw为风速;Cp(λ,β)为风电机组的风能利用系数,如式(3)所示,λ为叶尖速比,β为桨距角;ωr为风电机组转子转速。
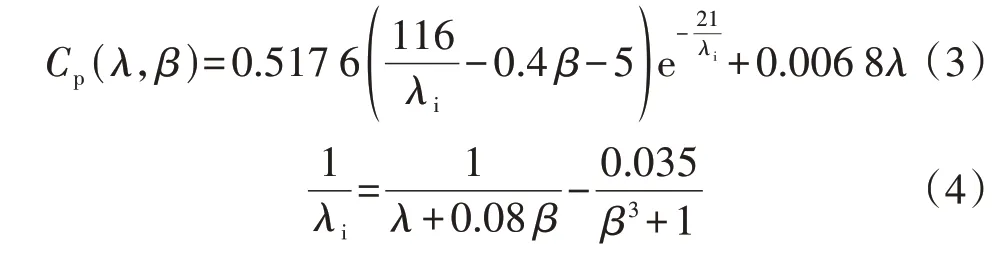
正常运行条件下,当风电机组转子转速ωr低于变桨距角控制的参考值ωmaxr时,桨距角β=0°,此时Cp仅与λ有关,对于给定的λ最佳值λopt,可得到Cp的最大值Cmaxp。当给定风速vw后,由式(2)可确定风电机组最佳转子转速。
忽略发电机的功率损耗,即发电机的机械功率和电磁功率相等,将式(2)代入式(1)可得到风电机组运行在MPPT运行点时的有功功率参考值Popt[16]为:
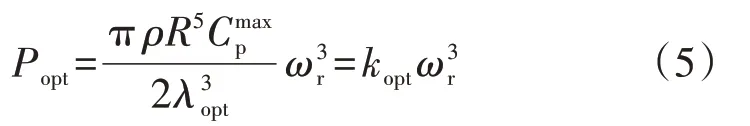
式中:kopt为风电机组运行在MPPT 运行点时的功率曲线系数,为常数。
2 减载控制
含高比例风电的电力系统需要风电机组提供一次调频,而风电机组运行在MPPT 运行点时,不具有功率备用,不能类似同步发电机提供一次调频,因此,若要使风电机组提供一次调频,则首先要使风电机组在稳态时具有提供一次调频的备用功率。
减载控制是一种使风电机组具有功率备用的有效方法。若对风电机组执行减载控制,则风电机组捕获的功率Pd为:

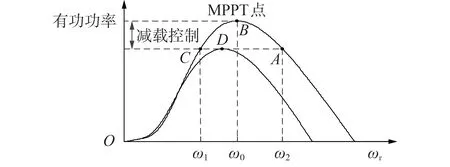
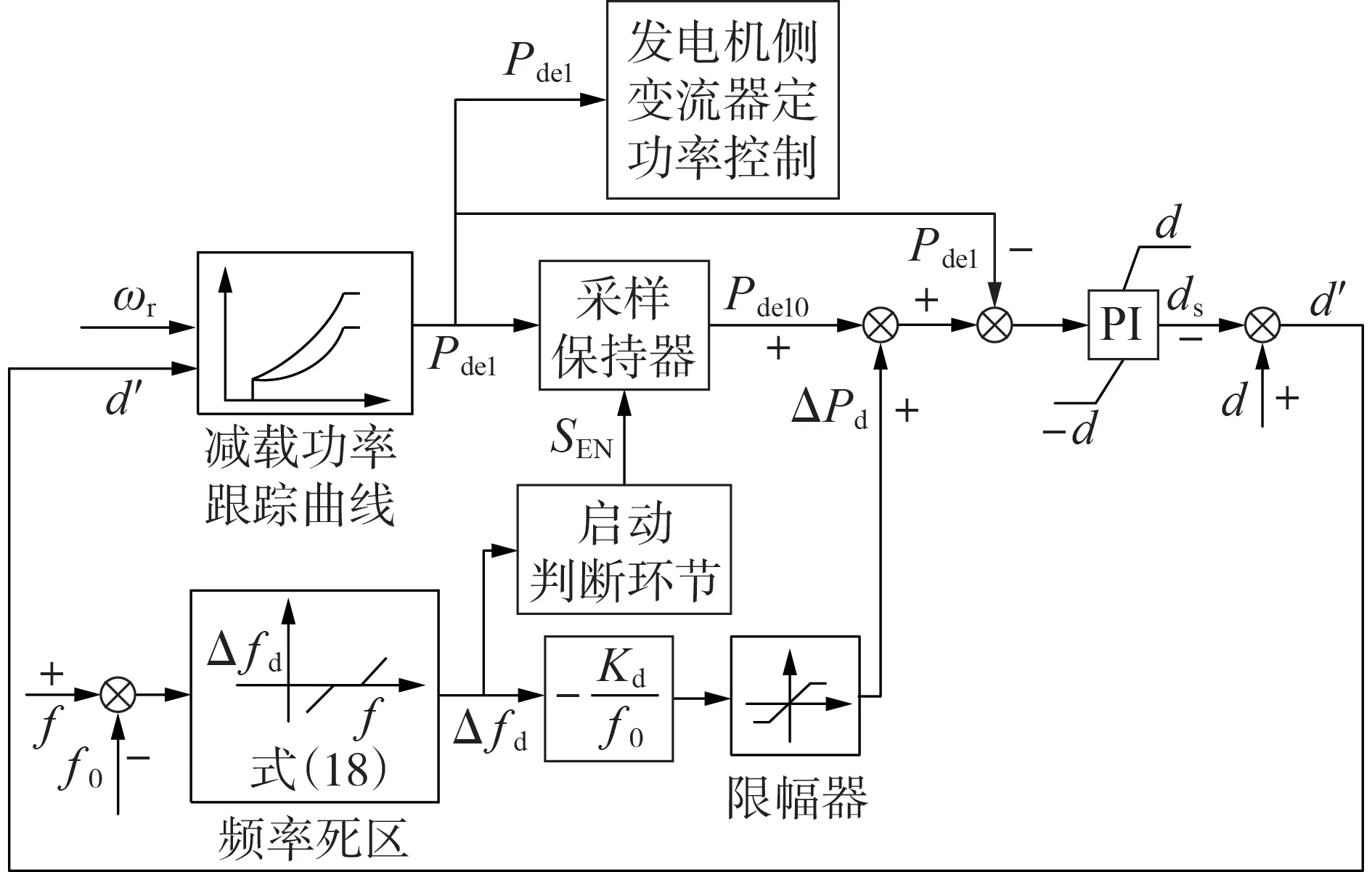
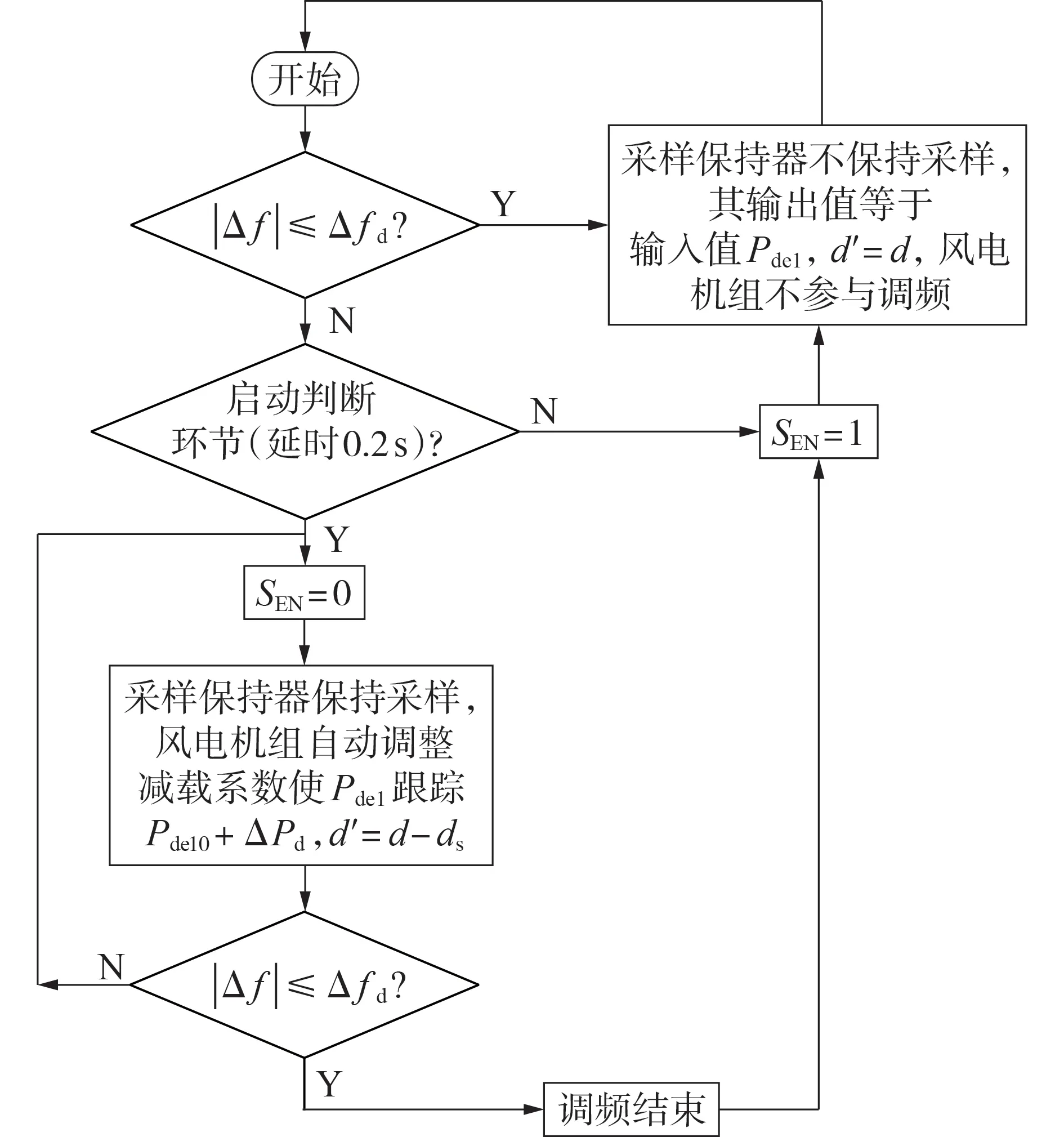
式中:d为风电机组的减载系数,0 由式(1)可知,当风速固定时,风电机组捕获的功率仅由风能利用系数决定,因此,对风电机组执行减载控制时其捕获的功率可以表示为: 式中:Cp_del为风电机组减载时的风能利用系数。 对比式(6)和式(7)可得: 式(8)表明,可以通过减小风电机组的风能利用系数实现对风电机组的减载控制。图1 为风速恒定时对风电机组执行减载控制的原理,图中点A对应的转速ω2大于MPPT 点对应的转速ω0,点C对应的转速ω1小于MPPT 点对应的转速ω0,点D对应的桨距角β1小于MPPT 点对应的桨距角β0=0°。由图可知,通过增加桨距角(点D)以及进行转子超速控制(点A)和转子减速控制(点C)均能降低风能利用率,实现对风电机组的减载控制。变桨距角控制通过增加桨距角来获得功率备用,当频率下降时,通过减小桨距角来增加捕获的功率。在转子超速控制下,当频率下降时,风电机组释放动能,当转子转速下降时,风电机组捕获的功率会增加,有利于风电机组的稳定运行。而转子减速控制会使风电机组运行在不稳定的点(点C),这是由于当频率下降时,风电机组释放动能,转速下降,导致捕获的功率进一步下降,从而使转速进一步下降。因此,本文采用变桨距角控制以及转子超速控制来实现对风电机组的减载控制。 图1 减载控制原理Fig.1 Principle of deloadding control 风速不同时,风电机组运行的转子转速也不同,实现减载控制的方式也不同。附录A 图A2 为风电机组参考功率与转子转速的关系图。图中:ωrb为中高风速和中低风速的分节点B对应的转速;ωin为风电机组并网的最小转子转速;ωmax为风电机组运行的最大转子转速,也为变桨距角控制的参考值,当转子转速ωr>ωmax时,变桨距角控制将会动作来限制转子转速的升高。 在低风速下,风电机组运行在附录A图A2中HI段时,减载控制不会使风电机组转子转速达到ωmax,仅通过转子超速控制就可实现所需的功率备用,变桨距角控制不动作,因此,风电机组减载时的风能利用系数与最大风能利用系数存在如式(9)所示的关系。 式中:λdel为风电机组减载时的叶尖速比。 忽略发电机的功率损耗,即发电机的机械功率和电磁功率相等,将式(2)代入式(7)可得到风电机组运行在HI段时减载控制的参考功率Pdel为: 将式(9)代入式(10)可得到Pdel为: 式中:k′opt为减载时的功率跟踪曲线系数,与风电机组的减载系数d和减载时的转子转速ωrdel(λdel=ωrdelR/vw)有关。当d确定后,ωrdel即可确定,从而k′opt也为确定的常数。 在中风速下,风电机组运行在附录A 图A2 中IJ段,风电机组转子转速为ωrb<ωr≤ωmax时,仅依靠转子超速控制不能满足对风电机组的减载控制要求,需要将转子超速控制与变桨距角控制结合。当转子转速达到额定转子转速时,变桨距角控制动作来限制转子转速的上升,此时的风能利用率为: 式中:βdel为减载控制时的桨距角。 将式(12)代入式(10)可得到与式(11)相同表达形式的功率参考值。 在高风速(小于极限风速)下,风电机组运行在附录A 图A2 中JK段,风电机组的转子转速为ωmax,转子转速已经不能再上升,只能依靠变桨距角控制来实现减载控制,此时的功率参考值为: 式中:Pmax为风机额定功率。 传统一次调频控制利用超速减载控制进行功率存储,利用下垂控制响应频率,其控制框图如附录A图A3所示。 式中:Pref1为传统一次调频控制后的参考功率;ΔPd为下垂控制的附加功率;Kd为下垂系数;f为实测的电网频率;f0为电网额定频率。 然而,这种超速减载控制与下垂控制结合的传统一次调频控制,存在功率跟踪曲线与下垂控制间的交互影响,这导致风电机组一次调频控制响应能力减弱以及风电机组减载储存的功率不能充分释放。下面以风电机组运行在附录A 图A2 的AB段进行分析。 由式(11)可知,扰动前风电机组的输出功率Pwt1为: 式中:ωr1为扰动前的风电机组转子转速。 根据式(11)和式(14),风电机组提供一次调频控制时的输出功率Pwt2为: 式中:ωr2为风电机组提供一次调频控制时的转子转速。 风电机组传统一次调频控制提供的实际附加功率ΔPy为: 图2 为频率降低时传统一次调频控制下风电机组的运行特性。图中:点E为调频前的稳态运行点,对应的转子转速为ωr1;点F为频率支持阶段的任意一点,对应的转子转速为ωr2;点G为风电机组机械功率和电磁功率达到的新的平衡点(不考虑二次调频),对应的转子转速为ωr3;点H为转子转速为ωr2时减载功率跟踪曲线上获得的参考功率对应的点;带箭头曲线表示风电机组提供频率支撑时的轨迹。由图可知,当频率降低(Δf<0)时,风电机组提供一次调频支撑,在下垂控制(ΔPd>0)的作用下,风电机组的电磁功率增加,而调频初始时刻机械功率不变,这时电磁功率大于机械功率,转子转速下降,捕获的风电功率沿着曲线上EG段增加(机械功率增加),但从减载功率跟踪曲线上获得的参考功率沿着曲线上EH段降低,在达到新的平衡前,转子转速下降,风电机组捕获的机械功率增加,电磁功率下降。当电磁功率等于机械功率时,风电机组进入新的稳定状态(点G),对于频率支撑过程中的任意一点F,对应的转子转速ωr2小于调频前的ωr1,ΔP1<0,而ΔPd>0,因此ΔPy<ΔPd。同理,当频率升高(Δf>0)时,ωr2>ωr1,ΔP1>0,而ΔPd<0,因此|ΔPy|<|ΔPd|。由此可见,功率跟踪曲线与下垂控制间的交互影响使风电机组传统一次调频控制提供的实际附加功率小于下垂控制的附加功率,导致在调频过程中不能充分释放减载控制储备的功率,削弱了一次调频控制的效果。 图2 频率降低时传统一次调频控制下风电机组的运行特性Fig.2 Operation characteristics of wind turbine with traditional primary frequency control when frequency reduces 为了消除上述超速减载控制的功率跟踪曲线与下垂控制间的交互影响,本文提出基于减载系数变化的一次调频控制策略,控制框图如图3 所示,流程图如图4 所示。图3 中:ds为采用所提一次调频控制计算出的减载变化系数:d′为风电机组的实际减载系数,为d与ds之差;SEN为所提一次调频控制的启动判断环节输出信号;Pdel0为风电机组调频前的初期参考功率。当SEN=1 时,采样保持器不保持采样,其输出值等于输入值Pdel,当SEN由1 转换为0 时,采样保持器保持采样,此时其输入值为Pdel0,并且其输出值将会一直保持为Pdel0,直到SEN由0变为1。启动判断环节用于控制采样保持器的启动或者退出,只有在风电机组提供一次调频控制时才启动采样保持器(SEN=0),在其他情况下,不启动采样保持器(SEN=1)。有多种方法可以启动采样保持器,本文中当频率偏差超过频率死区Δfd时,延时0.2 s 启动采样保持器,频率死区的设置方法如式(18)所示。 图3 基于减载系数变化的一次调频控制框图Fig.3 Block diagram of primary frequency control based on deloadding coefficient variation 图4 基于减载系数变化的一次调频控制流程图Fig.4 Flowchart of primary frequency control based on deloadding coefficient variation 式中:ΔfV为死区大小。 由图3、4 可知:当频率偏差在频率死区Δfd之内时,SEN=1,风电机组不启动一次调频控制,采样保持器的输出值为Pdel,下垂控制的输出值ΔPd=0,此时比例积分PI(Proportion-Integral)控制器的输入值为0,输出值ds也为0,风电机组的实际减载系数d′等于减载系数初始值d;当频率偏差超过死区Δfd时,延时0.2 s 启动采样保持器,SEN=0,风电机组启动一次调频控制,此时PI 控制器的输入值不为0,ds也不为0,d′=d-ds,风电机组自动调整减载系数使Pdel跟踪Pdel0+ΔPd,同时为了避免过度释放风电机组减载所储备的功率,设置PI控制器限幅值为±d。 与传统一次调频控制相比,在频率支撑阶段,本文所提一次调频控制下风电机组提供一次调频支撑的附加功率与转子转速无关,仅与频率偏差有关,能够较好地消除功率跟踪曲线与下垂控制间的交互影响。 图3 中,风电机组的下垂系数Kd和减载系数初始值d的选取尤为关键,二者是决定风电机组一次调频能力的重要参数。 同步发电机是通过调速器的下垂特性实现一次调频的,因此,参考同步发电机功率-频率静特性系数的定义,风电机组的下垂系数可表示为: 式中:δw为风电机组的静态调差系数。参考汽轮机组静态调差系数的取值范围,δw取值范围为0.04~0.06,对应的下垂系数Kd的取值范围为16.67~25。 δw还可以表示为: 式中:ΔPw为频率偏差Δf下风电机组增发的功率;负号表示ΔPw与Δf变化趋势相反。 风电机组一次调频稳定输出的最大功率等于风电机组减载所储备的备用功率ΔPdel,由式(20)可知,ΔPdel可表示为: 式中:Δfdmax为一次调频所能覆盖的最大频率偏差。 将风电机组减载所储备的备用功率ΔPdel转化为风电机组的减载系数d,如式(22)所示。 为了验证所提控制策略的准确性,在PSCAD/EMTDC 中搭建如附录A 图A4 所示的仿真系统,包含1 台PMSG、1 台同步发电机、1 个固定负荷和1 个可投切负荷。PMSG 的参数如附录B 表B1 所示。同步发电机采用7 阶模型,相关参数如附录B 表B2 所示。固定负荷PL1=3+j0.3 MV·A,可变负荷PL2=0.15+j0.015 MV·A。风电机组的下垂系数Kd=20,备用功率ΔPdel=0.06 p.u.,Δfd=0.05 Hz,Δfdmax=0.2 Hz。 在风速为8.3 m/s 下,10 s 时突然增加5%的可变负荷,图5为风电机组MPPT无附加控制、MPPT下垂控制、传统一次调频控制(减载控制+下垂控制)、所提基于减载系数变化的一次调频控制的仿真结果。图中:Pwt为风电机组的输出功率;Pwt、Pwind、ωr均为标幺值。令fnadir为频率最低点,f∞为扰动后的稳态频率,图5(a)中:MPPT 无附加控制的fnadir=49.06 Hz,f∞=49.88 Hz;MPPT 下垂控制的fnadir=49.59 Hz,f∞=49.87 Hz;传统一次调频控制的fnadir=49.75 Hz,f∞=49.90 Hz;所提一次调频控制的fnadir=49.79 Hz,f∞=49.91 Hz。 图5 中低风速下突然增加5%的负荷时的仿真结果Fig.5 Simulative results for 5% sudden load increase under medium- and low-wind speed 由图5 可知:当风电机组运行在MPPT 无附加控制时,风电机组不响应频率,最大频率偏差达到0.94 Hz;当风电机组运行在MPPT 下垂控制时,通过释放储备在转子中的旋转动能使最大频率偏差降到0.41 Hz,相较于MPPT 无附加控制降低了56.4%。由图5(b)和图5(c)可知,由于没有功率备用,当转子转速下降时,风电机组捕获的功率不仅没有增加反而下降,这导致在频率恢复的过程中风电机组从电网中吸收的能量(图5(b)中竖线阴影部分的面积)比频率支撑阶段释放的能量(图5(b)中横线阴影部分的面积)要多,这也直接导致了频率波动的时间较长,并且出现了轻微的二次频率跌落现象。对风电机组执行减载控制后,风电机组储备了0.06 p.u.的备用功率,转子转速提高,但还没有达到额定值,因此变桨距角控制不会动作,桨距角保持为0°(如图5(e)所示)。由于有备用功率,当频率恢复时,传统一次调频控制没有从系统中吸收能量,并且在转子转速下降时风电机组捕获的功率增加,最大频率偏差降到0.25 Hz,相较于MPPT 无附加控制降低了73.4%,且稳态频率提升了0.02 Hz,但是由于在一次调频过程中转子转速会下降,因此,从功率跟踪曲线获得的参考功率会下降,这削弱了传统一次调频控制的效果。由图5(a)和图5(b)可知,传统一次调频控制的频率改善效果比本文所提一次调频控制要差,并且风电机组储备的功率释放量也比所提一次调频控制要少,所提一次调频控制下的最大频率偏差降到0.21 Hz,相较于无附加控制降低了77.7%,相较于传统一次调频控制降低了16%。此外,由图5(b)和图5(c)可知,在稳态频率时,相较于传统一次调频控制,本文所提一次调频控制下风电机组的输出功率和捕获的功率均要高,稳态频率提高了0.01 Hz。综上,本文所提一次调频控制优于传统一次调频控制。 在风速为10 m/s 下,10 s 时突然增加5%的可变负荷,附录A图A5为风电机组MPPT无附加控制、MPPT 下垂控制、传统一次调频(减载控制+下垂控制)、所提基于减载系数变化的一次调频控制的仿真结果。 由图A5 可知:当风电机组运行在MPPT 无附加控制时,风电机组不参与频率调节,最大频率偏差达到0.87 Hz;当风电机组运行在MPPT 下垂控制时,风电机组通过释放储备在转子中的动能,最大频率偏差降到0.39 Hz,相较于MPPT 无附加控制降低了55.2%。由图A5(c)可知,由于没有功率备用,当转子转速下降时,风电机组捕获的功率下降,但下降幅度没有中低风速下的大。由图A5(b)可知,在频率恢复的过程中,相较于中低风速,中高风速下风电机组从电网中吸收的能量(图中竖线阴影部分的面积)要少,频率波动时间要短,频率波动幅度也要小,这是由于中高风速下转子转速较高,在释放相同的能量下,转子转速下降幅度更小,从而使捕获的风能损失量也更小,这说明风电机组MPPT 运行的调频能力与风速相关,在MPPT 运行下,要慎重选取风电机组的下垂系数。对风电机组执行减载控制后,转子转速提高到额定值,变桨距角控制动作来限制转子转速的上升(如图A5(e)所示)。由于有备用功率,当频率恢复时,传统一次调频控制下的最大频率偏差降到0.23 Hz,相较于MPPT 无附加控制降低了73.6%,且稳态频率提升了0.03 Hz。本文所提一次调频控制下的最大频率偏差降到0.2 Hz,相较于MPPT 无附加控制降低了77%,相较于传统一次调频控制降低了13%,证明了本文所提一次调频控制的控制效果优于传统一次调频控制。结合图5 的仿真结果可知,在中高和中低风速下,所提一次调频控制的暂态频率偏差和稳态频率偏差几乎相等,这表明该控制不受风速的影响。 在风速为8.3 m/s 下,10 s 时突然减少5%的可变负荷,附录A图A6为风电机组MPPT无附加控制、MPPT 下垂控制、传统一次调频(减载控制+下垂控制)、所提基于减载系数变化的一次调频控制的仿真结果。 由图A6 可知:当风电机组运行在MPPT 无附加控制时,风电机组不响应频率,最大频率偏差达到0.92 Hz;当风电机组运行在MPPT 下垂控制时,最大频率偏差降到0.34 Hz,相较于MPPT 无附加控制降低了63%。由图A6(c)可知,与图5中负荷突然增加的结果不同,风电机组捕获的功率与调频所需功率同调(当频率上升时,风电机组捕获的功率减少),这有利于调频,但频率峰值降低的幅度没有另外2 种减载控制下的大。由图A6(b)可知,在频率恢复阶段,风电机组向外释放功率,这导致MPPT 下垂控制下频率恢复的时间最长。传统一次调频控制下,最大频率偏差降到0.26 Hz,相较于MPPT 无附加控制降低了71.7%,且稳态频率偏差减小了0.01 Hz,但是由于在一次调频过程中转子转速上升,因此,从功率跟踪曲线上获得的参考功率增加,这削弱了传统一次调频控制的效果。由图A6(a)和图A6(b)可知,所提一次调频控制下的最大频率偏差降到0.21 Hz,相较于MPPT无附加控制降低了77.2%,相较于传统一次调频控制降低了19.2%,并且所提一次调频控制下的稳态频率比传统一次调频控制减小了0.01 Hz,因此,本文所提一次调频控制优于传统一次调频控制。 本文提出一种基于减载系数变化的风电机组一次调频控制,得到如下主要结论。 1)传统风电机组一次调频控制直接将减载控制和下垂控制结合,存在功率跟踪曲线与下垂控制间的交互影响,会削弱风电机组的一次调频控制效果,并且在频率支撑阶段不能充分利用风电机组减载储存的功率。 2)所提基于减载系数变化的一次调频控制的频率支撑能力不受转子转速的影响,输出的附加功率仅与频率偏差和下垂系数有关,能够很好地消除传统一次调频控制下超速减载控制的功率跟踪曲线与下垂控制间的交互影响,所提一次调频控制的控制效果优于传统一次调频控制。在相同的减载量下,所提一次调频控制能够进一步提高风电机组的频率支撑能力。 附录见本刊网络版(http://www.epae.cn)。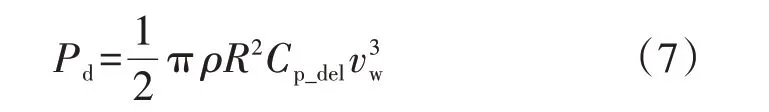

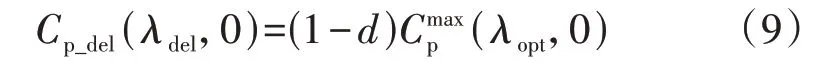

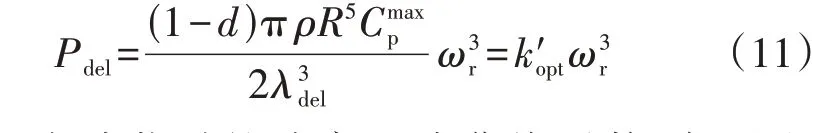

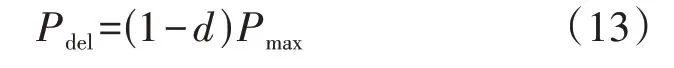
3 基于减载系数变化的一次调频控制
3.1 传统一次调频控制





3.2 基于减载系数变化的一次调频控制
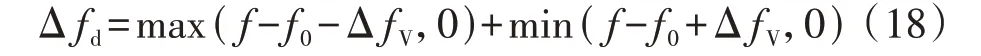
3.3 一次调频参数设置


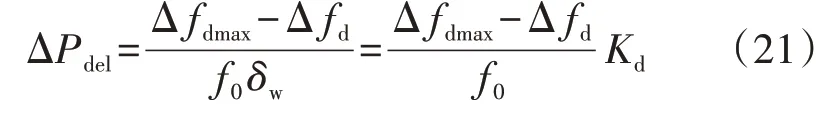
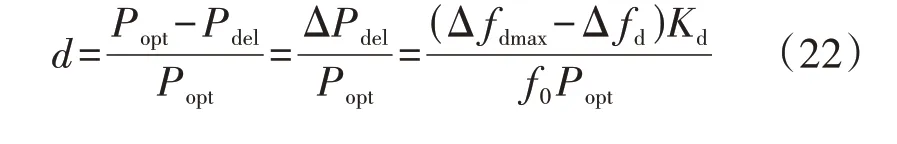
4 仿真分析
4.1 仿真模型
4.2 中低风速下负荷突然增加

4.3 中高风速下负荷突然增加
4.4 中低风速下负荷突然减少
5 结论

