基于设备模型辨识的新能源电力系统共模频率特征量化

张雯欣，吴 琛，黄 伟，高晖胜，辛焕海，

（1. 浙江大学工程师学院，浙江杭州 310027；2. 云南电网有限责任公司，云南昆明 650011；3. 浙江大学电气工程学院，浙江杭州 310027）

0 引言

随着新能源渗透率不断提高，电力系统惯量降低，调频能力弱化，这给系统频率稳定带来严峻挑战。为此，国内外学者提出多种新能源主动参与调频的控制策略以提升系统频率稳定性［1⁃2］。由于新能源调频特性与传统同步机有较大不同，这使得电力系统频率动态特性发生较大变化［3⁃4］。因此，如何在新能源高渗透率电力系统中量化分析频率响应值得研究。

目前，已有较多学者对该问题进行了研究［5⁃9］。例如，文献［7⁃8］提出了共模频率的概念以分析系统全局频率，并建立指标量化评估最低点等频率特征。但现有研究大多需基于系统中所有发电设备模型给定的假设，实际电力系统中可能存在部分设备模型未知的情况。此外，由于建模过程中的近似，分析过程中采用的模型也不一定能准确描述设备实际的调频动态。因此，为准确分析系统频率特征，需拓宽共模频率分析的适用场景，利用测量所得数据辨识获得发电设备模型来进行分析。

现有对同步机、新能源等发电设备模型进行辨识的研究中，关于同步机模型的辨识大多是针对调速器部分［10⁃11］，关于新能源则大多是针对其变流器控制系统［12⁃13］。例如：文献［10］提出一种基于实测试验数据的发电机调速器参数抗差分步辨识方法，可以有效减少数据中噪声毛刺偏差所带来的影响；文献［13］先是建立了变流器控制系统双输入（有功、无功功率差值）单输出（电压）传递函数模型，再通过辨识得到等效模型中的具体参数。需要指出的是，上述辨识方法皆是先根据待辨识设备运行机理估计其传递函数结构，再辨识得到具体参数，即采用灰箱建模方法。然而，为分析电力系统频率特征需辨识系统中类型多样的设备，估计所有设备传递函数结构不仅工作量大，而且可能存在部分设备模型“黑箱化”、运行机理不明难以估计的情况。因此，在大电网中辨识各模型更合适的方法可能是采用黑箱建模，即先找到适合描述多类型设备的通用模型形式，再逐一辨识参数。例如，采用输出误差OE（Output Error）模型、OE 滑动平均模型等［14⁃16］。然而，基于黑箱建模辨识所得模型一般只能用于计算系统惯量并分析频率初始变化率［14⁃16］，而难以用于评估频率最低点。这是因为系统的惯量可由各设备惯量简单求和得到，且初始变化率只与惯量相关。例如，文献［14］采用OE模型作为发电设备通用模型，基于此实现类噪声下的电网惯量常态化估计。但量化分析频率最低点需综合考虑所有调频动态环节。即使以通用的模型形式描述各种设备，由于参数的差异，系统频率响应模型阶数也非常高，难以进行分析。另外，各辨识模型调频作用对系统频率响应的影响也难以量化。因此，需对黑箱建模辨识得到的多类型发电设备动态模型进行简化。例如，将各设备模型简化为统一的传递函数结构，即几种选定的调频形式的线性组合（如惯量、阻尼与简化一次调频响应等）。这样将所有设备模型求和后来分析系统频率响应时，只需将各设备的各种调频形式对应参数相加即可，系统的阶数不会升高，由此可极大程度地降低频率特征解析的难度。

综上，本文拓宽了共模频率分析的适用场景，利用测量所得数据辨识获得发电设备模型，并结合系统实际工况变化来进行共模频率特征量化。首先，利用扰动后各设备并网接口实测运行数据（频率、功率响应信号），选择OE 模型描述所有待辨识发电设备。然后，使用辅助变量法并结合高斯-牛顿法进行迭代，消除噪声对测量数据的影响，实现各发电设备动态模型辨识，得到各设备频率-功率响应的传递函数。进一步地，结合系统实际工况变化（即设备的投切变化等），将辨识的模型简化为微分-比例-一阶滞后3 个环节组成的统一结构，并求解出各设备统一结构等效参数，得到形成表征系统共模频率响应特性的简化传递函数模型，进而实现系统频率平均变化率及频率最低点等频率特征量化。最后，通过仿真验证了上述基于设备模型辨识的新能源电力系统频率特征量化方法的有效性。

1 频率特征量化理论

1.1 系统共模频率响应分析

由于电力电子设备频率动态响应与传统同步机之间存在较大的差异，在新能源电力系统中如何定义、分析系统频率响应至今没有一个明确的结论。文献［6⁃8］等提出通过模态解耦的方法，从各节点频率响应中分解出一个表征全局频率的分量以分析系统频率响应特性。其中，文献［8］提出的“共模频率”方法可适用于含多样化设备的新能源电力系统，适用范围更广。因此，下文基于文献［8］中定义的共模频率进行分析。

综合考虑设备的频率-有功动态特性以及网络有功潮流后，共模频率可表示为［8］：

值得一提的是，当电力系统中存在大量恒阻抗负荷时，w/n与IT之间将有较大差异。此时，由共模频率表达式可知，不同节点的发电设备或扰动对系统共模频率有不同的影响权重。文献［8］中的分析及仿真结果表明，相比传统平均系统频率模型［6］等认为各节点等权重的分析方法，共模频率能更准确地表征系统全局频率响应。

1.2 发电设备模型辨识与化简需求

由式（1）可知，若要解析系统共模频率轨迹，需已知各设备模型。然而，实际电力系统中可能存在部分设备模型“黑箱化”的情况，此外，由于建模过程中的近似，在分析频率时采用的模型参数也不一定能准确描述设备的调频作用。因此，为准确分析系统频率特征，需将基于模型的共模频率分析进行延伸，利用实际系统可测得的已知量（频率、有功功率数据）辨识得到发电设备模型来进行共模频率分析。

另外，在新能源电力系统中，设备数量多且各设备模型差异大，将辨识所得模型求和求解的系统频率响应动态阶数非常高，频率最低点等频率特征难以量化，也难以分析各辨识模型调频作用对系统频率响应的影响。因此，需将多类型设备辨识模型进行简化，使得系统频率特征能够解析量化，并能够从系统层面分析各设备模型的调频贡献。

综上，一种可行的思路是采用黑箱建模，即先找到适合描述多类型设备的通用模型形式，实现各发电设备动态模型辨识。再进一步基于实际工况（即设备的投切情况等），将各设备化简为合适的统一结构模型（统一结构模型的选择与等效见1.3节），使辨识得到的各设备模型在系统中所起的调频作用能够通过几种选定的调频形式进行线性叠加。基于此，能从系统的角度分析辨识所得各设备调频贡献，使系统共模频率特征能够解析量化。

值得一提的是，对于同步机转子等旋转惯量，其动态将导致式（1）非真，即传递函数分子阶数大于分母阶数，不利于辨识。为此，可以考虑辨识该传递函数的逆，即以功率为输入、频率为输出，辨识各设备有功功率-频率传递函数。

1.3 简化频率特征分析的设备统一结构模型

为能够对各设备模型进行简化，实现从系统的角度分析各设备调频能力，采用文献［9］提出的统一结构模型。该模型基于系统共模频率轨迹的一般变化规律，使用由微分-比例-一阶滞后3 个环节组成的统一结构等值各种发电设备的频率-有功功率响应模型，其表达式如下：

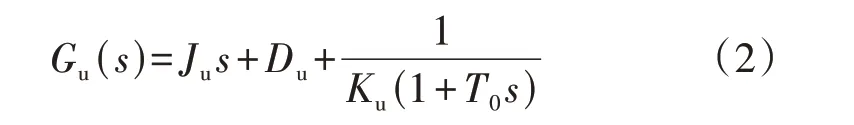
式中：Gu(s)为统一结构传递函数；Ju、Du和1/Ku分别为有效惯量、有效阻尼系数和有效静态调差系数；T0为调差时间常数（所有设备相同）。

简化模型参数的求解算法参考文献［9］。需要说明的是，有效参数含有“模态性”的性质（该性质是由通过低阶模型拟合高阶模型所引起的），设备的惯量、阻尼系数和静态调差系数会随着系统共模频率的变化而变化，需要将设备的调频能力投影到共模频率上才能得到有效参数，并确定它们对系统的真实贡献。结合文献［9］所提方法即可迭代求解出各设备统一结构的等效参数。

上述简化为统一结构的过程是用选定的几种调频形式的线性组合（惯量、阻尼与简化一次调频响应）在有限时间内来逼近设备的动态调频响应。因此，在完成各设备模型求和求解系统频率响应时，只需将各设备的各种调频形式对应参数相加即可。

因此，基于上述统一结构，将不同发电设备有效参数进行叠加，即可得到ΔPL为功率阶跃扰动（ΔPL=-P0/s，P0为扰动大小）下，系统频率响应Δω′cm为：

式中：Ju，i、Du，i和1/Ku，i分别为第i台发电设备有效惯量、有效阻尼系数和有效静态调差系数。

采用文献［9］所提频率特征量化方法，即可计算得到所关心的系统频率最低点Δωnadir、频率平均变化率Δω̇0～tp1（Δω̇0～tp1具体指0～tp1时段内频率平均变化率，满足Δω̇0～tp1=Δω(tp1)/tp1，Δω(tp1)为tp1时刻频率变化量，tp1为人为选取的扰动发生后的某时刻，可选取为出现一次频率最低点的时刻tnadir的1/3）等频率特征，进而分析系统频率稳定性。

此外，因实际电力系统中所测得的已知量（各设备并网点的频率与功率响应信号）包含多种差模分量（即表征节点频率相对振荡的分量），难以直接获得共模分量。由于统一结构的参数具有模态性，在输入信号存在差模分量的情况下，若直接由频率与功率响应信号求解出统一结构模型中对应的各参数，得到的统一结构模型参数将存在误差。而先利用设备并网点的有功和频率数据（含差模分量）辨识出与各发电设备实际动态特性一致的动态模型，再结合实际工况将所辨识的模型化简为统一结构时，能得到准确的模型辨识结果，将保证求解统一结构参数时迭代输入的共模频率的准确性，从而能有效量化系统共模频率特征。

2 发电设备的辨识模型选择与实现

选择合适的辨识模型结构与辨识方法是有效建立各设备动态模型的关键。下面详细介绍辨识各发电设备所用的OE模型、辨识方法及模型定阶方法。

2.1 发电设备的辨识模型选择

文献［18］指出辨识的四要素分别为：输入输出数据、模型、准则函数及优化方法。其中，模型是描述系统的主要手段，其类别多种多样，有线性与非线性、动态与静态、确定性与随机性、连续与离散、输入输出与状态空间等之分［18］。

由于实际系统往往存在随机干扰，选择随机系统模型描述各发电设备，其通用差分方程形式为［18］：

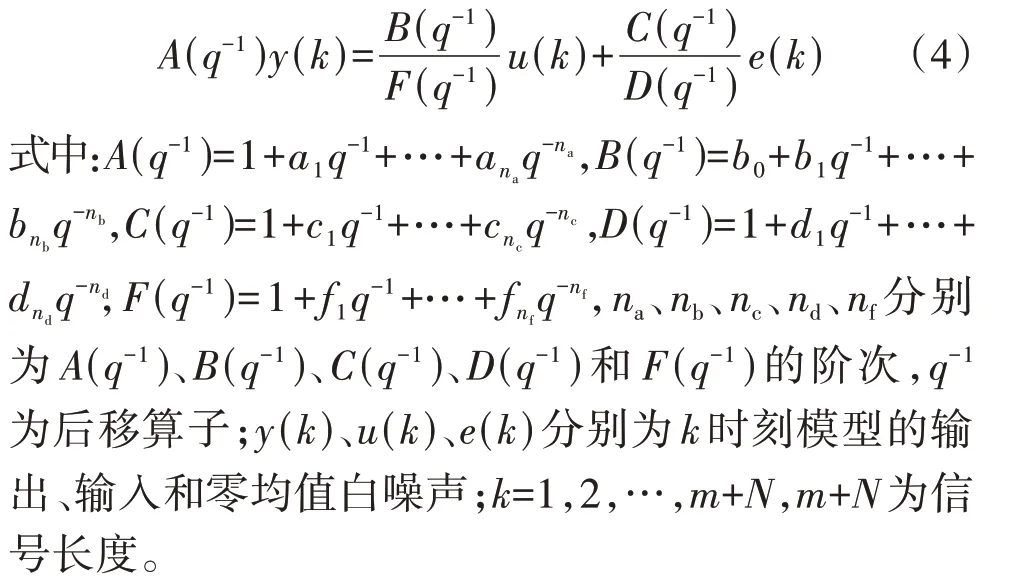
随机系统模型可分为如下3 类［18］：时间序列类模型、方程误差类模型与OE类模型。时间序列类模型输入变量多为随机白噪声，即B(q-1)=0，典型的有自回归模型(C(q-1)=D(q-1)=1)；方程误差类模型系统动态极点仅与A(q-1)有关，即F(q-1)=1，典型的有方程误差模型(C(q-1)=D(q-1)=1)与受控自回归滑动平均模型(D(q-1)=1)；OE 类模型系统动态极点仅与F(q-1)有关，即A(q-1)=1，典型的有OE 模型(C(q-1)=D(q-1)=1)与OE滑动平均模型(D(q-1)=1)。

考虑到实际电力系统中测量信号存在噪声，并且估计各设备动态模型只需将待辨识的动态模型参数化，无需估计噪声模型。本文采用OE模型来描述待辨识设备［14，18］，具体形式如下：

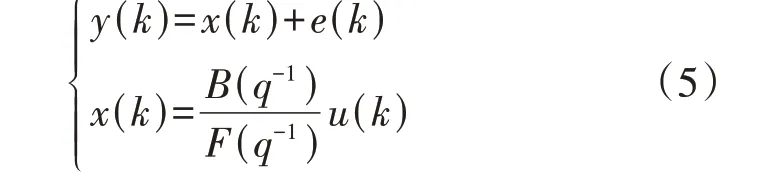
OE 模型包含了系统无噪输出x(k)，该模型在辨识单变量时具有待估计参数少与拟合度高等优点［14］。

2.2 基于OE模型的设备辨识

假设模型阶数nb、nf已确定（如何确定阶数见2.3节），此时式（5）的向量形式可描述为：

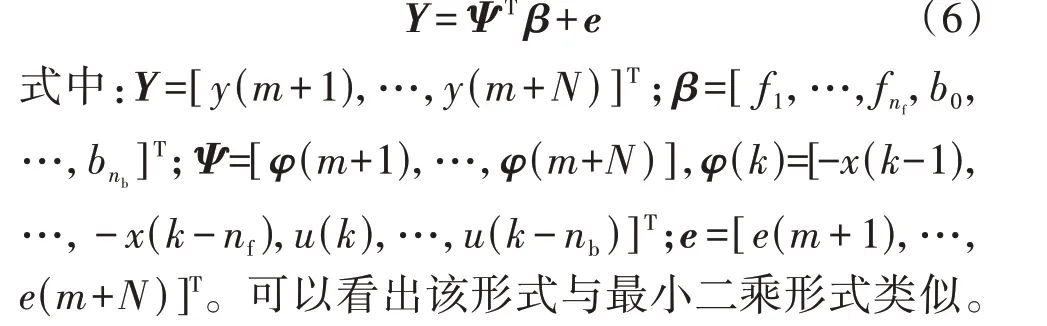
由于φ(k)包含无法观测到的x（k），因此无法直接由最小二乘法求解得到。本文采用高斯-牛顿法实现参数估计迭代，其主要思想是使用泰勒级数展开式近似地代替非线性回归模型［19］。通过多次迭代、多次修正回归系数β̂，使回归系数不断逼近非线性回归模型的最佳回归系数，最终使原模型的残差平方和达到最小，即：

上述方法能有效剔除噪声对测量信号的影响，并准确辨识出各发电设备有功功率到频率的动态模型参数。

不同发电设备辨识出的传递函数阶数与参数不同，将它们求和求解的系统频率响应动态阶数将非常高，难以进行量化分析。为此，需将各设备简化为统一的传递函数结构，使得各设备在系统频率响应中调频动态作用的求和能够通过统一结构中各环节对应参数进行线性叠加，以有效降低频率特征解析难度。

2.3 模型阶数定阶

由2.2 节可知，在进行模型辨识的过程中，模型阶数是人为设定的。为了减小由系统辨识阶次对辨识模型造成的偏差，本文应用赤池信息量准则AIC（Akaike Information Criterion）进行模型阶数的选择［14］。AIC 作为一种最通用的模型选择准则，其提供了权衡估计模型复杂度和拟合数据优良性的标准，具体表示如下：

式中：fAIC为AIC 评价结果；o=nf+nb+1，为辨识模型中参数的数量，与模型阶数有关；fSSR为实际值与预测值残差平方和。

由式（9）可知，fAIC的大小与模型的阶数以及模型的残差平方和有关，兼顾了所估计模型的简洁性与精确性。因此，优先选取使fAIC值最小的模型阶数。

3 基于设备模型辨识的系统频率特征量化流程

结合上文所述，得到基于设备模型辨识的电力系统各发电设备统一结构参数等效及系统共模频率特征量化评估流程图，见附录B 图B1。具体实施步骤如下。

1）数据采集：假设系统共有n台发电设备，假设模型已知的设备有j台，对模型已知的设备记录其频率-有功功率传递函数Gi(s)，i∈{1，2，…，j}；对于模型未知的设备，采集它们在电力系统发生负荷投切等扰动时并网点的有功功率ΔPi与频率波动数据Δωi，i∈{j+1，j+2，…，n}。

2）设备辨识：采用第2 节的方法，将有功功率信号ΔPi作为输入、频率波动信号Δωi作为输出，通过AIC 确定系统模型阶次，再辨识得到离散动态模型参数。进一步地，利用阶跃不变z-s变换将设备模型转换成连续传递函数形式，得到各设备有功功率-频率的传递函数，取其倒数得到各设备频率-有功功率传递函数。

3）统一结构参数等效：结合电力系统实际工况（如各发电设备投入情况），基于辨识出的各设备模型及已知模型，利用文献［9］的优化迭代方法，将各设备等效成统一结构模型，并得出对应的统一结构参数以量化各设备调频贡献。

4）频率特征指标计算：将各设备参数进行叠加得到系统的统一结构参数，然后进行共模频率特征指标计算。

4 算例分析

4.1 仿真系统

基于MATLAB／Simulink 搭建10 机39 节点系统仿真模型。仿真系统的网络拓扑结构与标准的新英格兰系统相同［8］。在仿真系统中使用了如下3 种发电设备：同步机、跟网型变流器及构网型变流器。具体频率-有功功率传递函数见附录C，各发电设备主要参数见附录C 表C1，压缩拉普拉斯矩阵左特征向量参考文献［8］。取容量基准值SB=1 000 MV·A，所有设备的容量均设为1000 MV·A。

为验证本文基于设备模型辨识的新能源电力系统共模频率特征量化方法的有效性，设置如下算例。

算例1：G1、G3、G5、G7、G9、G10为同步机，G2、G4为跟网型变流器，G6、G8为构网型变流器；考虑的扰动为t=1 s时，G8有功功率参考值突降0.3 p.u.。

算例2：在算例1的基础上，将投入运行的G6、G8替换为跟网型变流器。

算例3：在算例2 的基础上，将扰动替换为t=1 s时，G9有功功率参考值突降0.3 p.u.。

算例4：在算例1 的基础上，将投入运行的G8替换为同步机。

4.2 基于辨识模型的频率特征量化方法准确性验证

测量算例1 中各台发电设备并网处频率波动Δω与有功功率波动ΔP。为保证该数据能够充分反映发电设备的有功功率-频率动态过程，取扰动发生后25 s内的测量数据。

图1 对比了G1、G2、G6、G9并网处实际测量频率轨迹与基于本文方法辨识得到的各设备动态模型下拟合的频率轨迹。由仿真结果可知，基于本文方法辨识得到的各发电设备有功功率-频率传递函数模型拟合度误差皆在5%以内（使用拟合优度R2评价拟合度，R2=1-fSSR/fTSS，其中fSSR为实际值与预测值残差平方和，fTSS为实际值与其均值的离差平方和）。

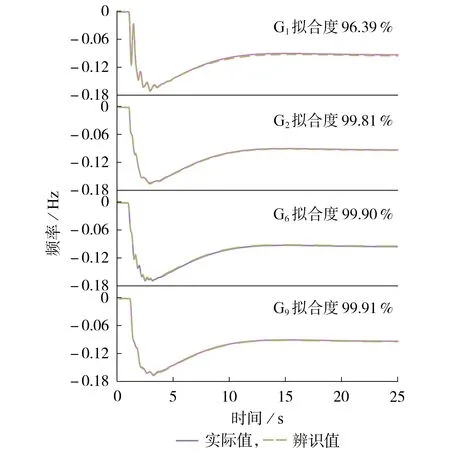
图1 各设备频率轨迹对比图Fig.1 Comparison of frequency trajectory of each device

为验证辨识模型的准确性，比较辨识得到的各设备频率-有功功率传递函数与实际的频率-有功功率传递函数的Bode 图如图2 所示。由图可见，辨识得到的各设备模型在幅频特性及相频特性方面都与实际模型基本吻合。该结果说明了辨识所得设备模型的动态特性与实际相接近，证明了辨识所得设备模型的准确性。

基于最小二乘法［16］得到的发电设备辨识结果见附录C图C2和图C3，将其与基于本文方法得到的发电设备辨识结果（图1和图2）进行对比分析可知，本文方法对算例中多种发电设备模型的辨识结果精度更高。

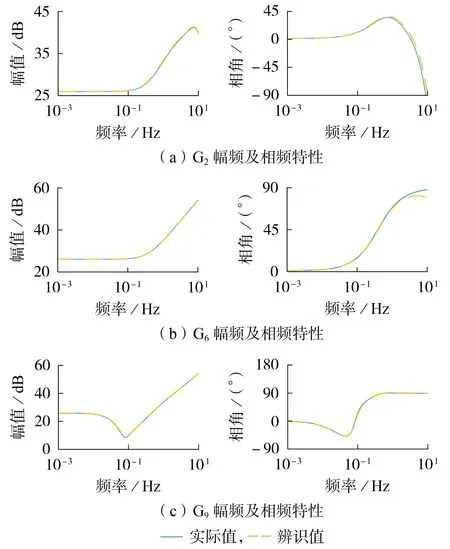
图2 辨识模型验证Fig.2 Verification of identified model

进一步地，利用辨识出的各设备动态模型，结合4 种算例工况，计算得到不同算例下系统统一结构参数与等效扰动值如表1 所示，表中Jus、Dus、1/Kus、T0、P0均为标幺值。各设备等效统一结构参数如附录C表C2所示。

表1 不同算例下统一结构参数与等效扰动结果Table 1 Unified structure parameters and equivalent disturbance results under different cases

对比不同算例下通过仿真获得的系统共模频率（简称为共模频率）以及基于统一结构计算得到的系统频率轨迹（简称为统一结构）如图3所示。

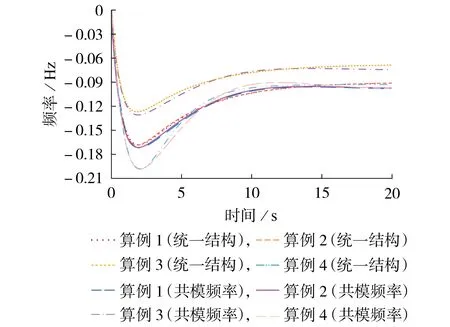
图3 系统共模频率轨迹对比Fig.3 Comparison of system common mode frequency trajectory

取tp1=tnadir/3，仿真得到的共模频率动态特征与基于统一结构计算得到的频率动态特征对比如表2所示。

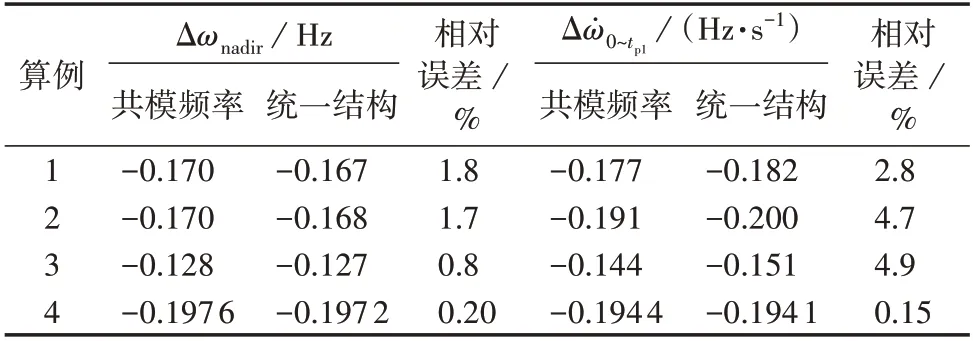
表2 频率动态特征对比Table 2 Comparison of frequency dynamic characteristic

由表2 可以看出，由统一结构计算得到的与系统仿真共模频率中频率最低点的相对误差及频率变化率的相对误差均在5%以内，其精度满足工程应用需求。上述结果表明，本文所提的基于设备模型辨识的电力系统频率特征量化方法首先能够利用电力系统中测得的功率、频率波动数据，准确辨识出不同类型发电设备的动态模型。并能根据系统实际工况，量化各设备调频贡献，进一步完成不同算例下共模频率特征量化工作，实现共模频率分析的实际应用。

4.3 抗噪声干扰性验证

为验证本文方法的抗噪声干扰能力，在算例1测得的功率、频率波动数据中注入白噪声（其幅值为测量信号的6%）以模拟实际系统中的相量测量装置（PMU）测量噪声。利用辨识后得到的G2、G6、G9动态模型在功率波动输入下拟合的频率轨迹与各并网点频率轨迹对比图见附录D 图D1，设备相频特性与幅频特性对比图见附录D图D2。由图D1和图D2可知，在输入输出数据存在噪声的情况下，基于本文方法辨识得到的各发电设备频率-有功功率传递函数模型同样较为准确，辨识所得设备模型的动态特性与实际相接近。

5 结论

本文利用各发电设备并网点有功功率及频率波动数据辨识得到各设备动态模型，并进一步简化为统一结构模型以量化新能源电力系统共模频率特征，得到如下结论。

1）应用OE模型描述待辨识设备动态模型，并利用辅助变量法及高斯-牛顿迭代能辨识多类型发电设备动态调频特性。进一步地，结合统一结构简化方法能够将辨识得到的多类型设备调频能力叠加，进而可量化分析系统的频率特征及各设备的调频贡献。

2）本文方法拓宽了共模频率分析的适用场景，利用测量所得数据辨识获得发电设备模型来进行共模频率特征量化。该方法可以弥补实际系统模型不准确与“黑箱化”的问题，且可以结合实际工况变化对系统共模频率进行量化，能够对未来电力系统中可能发生的频率失稳问题进行预警，有利于共模频率分析的实际应用。

此外，本文研究中均假设设备模型呈线性，如何针对非线性模型（如考虑调速器死区）修正辨识结果、完善频率特征分析方法值得进一步研究。

附录见本刊网络版（http：//www.epae.cn）。