基于BP神经网络的高速铁路无砟轨道砂浆层离缝损伤识别

高建敏，金忠凯,2

(1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031；2.中国人民解放军第五七一九工厂，四川 成都 611936)

无砟轨道以其高平顺、高稳定性以及养护维修量小等特点，在我国高速铁路建设中得到了广泛的推广和应用。然而，随着高速铁路运营时间和运营里程的增加，无砟轨道也出现了一些服役问题，CRTSⅡ型板式无砟轨道砂浆层离缝就是其中之一[1]。CA砂浆层是CRTSⅡ型板式无砟轨道的重要组成部分，也是最为薄弱的部分，较容易发生损伤。在砂浆层离缝损伤发生的初期，砂浆层与轨道板间仅在温度荷载作用下产生粘结失效，轨道板并未产生翘曲变形，对高速车轨系统的动力影响可能较小。但当砂浆层与轨道板间发生粘结失效后，在温度和列车荷载的共同反复作用下，离缝损伤逐渐加重，进而使轨道板产生翘曲变形，当高速车辆经过时，离缝区轨道板与砂浆层间将呈脱空状态，致使轨道结构的受力、传力等都将随之发生变化，由此加剧轮轨系统的振动[2]。若不对其及时修复，在列车荷载和温度荷载的长期、反复和共同作用下，轨道结构损伤将进一步加重，从而影响高速铁路轨道结构的服役性能，进而影响高速行车的舒适性和安全性。因此，及时掌控轨道板与砂浆层间的离缝损伤问题并对其进行适时的修复或维修显得十分重要。

CA砂浆层位于轨道板和底座板之间，厚度较薄、位置较为隐蔽，若损伤较小或者损伤位置未发生在板端暴露处，则通过肉眼检查的方法很难直接观测到，实验检测方法又比较消耗时间、投入成本较大[3]。因此，探索一种能够快速、准确识别CA砂浆层离缝损伤与否以及离缝损伤程度的方法显得也十分有必要。

近年来，国内学者针对轨道板与砂浆层间离缝的成因及其发展、离缝形成后轨道板与砂浆层间受力以及轨道结构的振动和服役性能等开展了较多研究工作[4-7]，但是，对离缝损伤智能化检测、识别等开展的研究工作相对较少。钟鹏飞等[8]基于弹性波在多层介质中的传播特性，提出了一种基于弹性波的检波器阵列式组合的CA砂浆层离隙病害快速检测方法。范岩旻等[9]基于高铁线下结构标准设计，提出了一种基于模式匹配法的CA砂浆层脱空及离隙网格化扫描检测方法。廖红建等[10]结合CRTSⅡ型板式无砟轨道结构特征，应用时域有限差分法，建立了探地雷达正演数值计算模型，并应用该模型分析了无砟轨道砂浆层缺陷和路基沉降病害的探地雷达图像特征。上述针对高速铁路轨道结构损伤、病害的检测方法可以有效地检测到离缝、脱空等损伤、病害的发生位置及其范围，但是无法准确识别离缝等损伤在垂直方向的破坏程度，也无法掌握离缝损伤与行车动力性能间的动态关系。

随着智能化识别需求的提高，神经网络技术得到不断发展和应用。神经网络技术不仅可以表达线性映射关系，还可以表达复杂的非线性映射关系。相较于传统的损伤识别方法，其不必建立结构响应与物理参数之间的函数关系，只需确立输入与输出量之间某种线性或非线性映射关系即可，因此，其应用范围较为广泛[11-12]，近年来其在结构损伤识别领域、铁路状态监测等方面亦得到关注和应用。Elkordy等[13]建立了含损伤的五层框架结构三维模型，提取了模型的振型变化量作为输入，通过建立BP神经网络进行了五层框架结构损伤位置及损伤程度的识别研究。Barai等[14]应用神经网络系统对结构振动输出数据进行处理，分析了结构在不同工况下的振动特性，验证了神经网络系统在数据处理方面的优势。孙宗光等[15]、闫桂荣等[16]、Manning等[17]通过仿真并提取不同构件的损伤参数，并将损伤参数作为神经识别网络模型的输入开展了构件损伤位置和程度的识别研究。裴国史[18]基于神经网络基本理论和车辆-轨道耦合动力学理论，以仿真获得的谐波不平顺激扰下车辆系统动力学响应为输入，分析了基于神经网络技术的谐波不平顺状态识别方法，对比了模式识别、径向网络识别、时间序列预测和BP神经网络四种模型预测识别效果差异。单文娣[19]研究了以有限元计算得到的车轨系统动力响应作为输入，应用神经网络识别对路基沉降进行识别的可行性。彭丽宇等[20]则基于BP神经网络方法对轨道不平顺预测开展了研究。

综上分析可见，高速铁路轨道服役状态的智能化分析、检测已成为当前铁路发展的迫切需求，而应用神经网络等现代技术进行高速铁路轨道损伤状态的分析和研究工作尚不充分。为此，本文基于车辆-轨道耦合动力学理论[21]和BP神经网络技术，通过建立高速车辆-CRTSⅡ板式无砟轨道耦合动力学模型，分析不同程度砂浆层与轨道板间离缝损伤对高速车轨系统动力响应的影响规律，探寻对离缝损伤敏感的动力响应指标，进而建立用于离缝损伤识别的BP神经网模型，开展CRTSⅡ型板式无砟轨道砂浆层离缝损伤识别研究，以期为高速铁路板式无砟轨道离缝损伤病害的检测分析及其养护维修等提供理论参考。

1 模型构建

基于BP神经网络技术进行高速铁路板式无砟轨道CA砂浆层离缝损伤识别研究所需模型主要包括两大部分:①基于车辆-轨道耦合动力学理论建立的高速车辆-板式无砟轨道耦合动力学模型，用于进行不同轨道损伤状态下高速车轨系统的动力响应分析，寻找对轨道结构损伤敏感的动力响应指标以及获得该指标在不同损伤状态下的动力响应规律，进而应用于神经网络模型输入；②用于识别分析的BP神经网络模型。损伤识别流程见图1。

图1 基于BP神经网络的板式无砟轨道离缝损伤识别流程

1.1 含离缝损伤的高速车辆-板式无砟轨道动力学模型

应用车辆-轨道耦合动力学理论，建立了包含离缝损伤的高速车辆-板式无砟轨道耦合动力学模型。模型包括5个部分，从上到下依次是车辆子模型、轮轨相互作用关系、轨道不平顺激扰模型、无砟轨道子模型以及轨道板与砂浆层间离缝损伤模型。其中，车辆子模型包含一个车体、前后2个转向架和4个轮对，考虑车体的点头和沉浮运动、前后转向架的点头和沉浮运动以及4个轮对的沉浮运动，共10个自由度；一系、二系悬挂的刚度和阻尼采用弹簧和阻尼来模拟[21]。轮轨相互作用关系是车辆子系统与轨道子系统间的连接纽带，采用Hertz非线性弹性接触理论来进行计算[21]。轨道不平顺是轮轨系统振动的重要激扰源，选用随机不平顺激扰，依据中国高速铁路无砟轨道平均谱(63.2%百分位数谱)变换获得[21]。板式无砟轨道子模型由钢轨、轨道板、CA砂浆层和底座板组成，其中，钢轨被看作是连续弹性离散点支承上的无限长Euler梁；轨道板被简化为有沿钢轨纵向连续分布的线性阻尼的弹性地基上的自由梁；钢轨与轨道板间经由扣件系统相连，能起到缓和冲击振动的作用；砂浆层位于轨道板和底座板之间，起着层间连接及承受结构内垂向力、减缓振动之作用；整个板式无砟轨道子模型可看作垂直方向上的弹性基础叠合梁[22]。

当无砟轨道板与砂浆层之间产生脱粘后，层间连接减弱。在温度载荷、列车动载荷及外界环境(如雨水冲刷)作用下，轨道结构继续劣化，轨道板的翘曲变形受到的约束减小。CRTSⅡ型板式无砟轨道板之间通过宽窄接缝连接，此处连接较弱，因此，在宽窄接缝处两轨道板容易产生上拱变形，轨道板与砂浆层完全分离，损伤后的结构示意见图2。轨道板上拱变形后使钢轨也随之发生变形，在垂向产生高低不平顺，车辆经过离缝区时会引起整个系统的激扰振动，这对轨道结构服役性能、轮轨动态相互作用和车辆运行平稳性等都是不利的。

图2 离缝上拱损伤时轨道结构示意

离缝上拱变形后，车轨耦合程序中需要考虑离缝损伤引起的轨道板初始上拱位移，并且需重新编写离缝段的刚度矩阵。根据文献[24]，拟合离缝上拱波形、实测离缝上拱波形以及采用余波模拟离缝上拱波形计算得到的振动响应差别不大。因此，本文选用余弦波形来模拟离缝处轨道板的上拱波形，其描述公式为[22]

(1)

式中：u0为砂浆层与轨道板之间的垂向相对位移；a为层间离缝上拱的幅值；L为层间离缝上拱的波长；v为车辆运行速度；t为时间。

重新编写后，离缝上拱区单元刚度为[22]

(2)

式中：u为砂浆层的厚度；F为砂浆层上的作用力。

1.2 BP神经网络模型

砂浆层离缝损伤引起的结构振动响应与离缝损伤之间为非线性映射关系，由于BP神经网络在非线性映射问题方面功能强大，而且现阶段模型发展较为成熟，故选用BP神经网络对砂浆层离缝损伤进行判断。

BP神经网络是一种按照误差逆传递算法进行训练的多层前馈网络，是目前应用最广泛的神经网络模型之一[23]。BP神经网络能训练、存贮大量输入与输出之间的映射关系，无需先计算或推导描述这种映射关系的表达式[25]。它的学习规则是使用最速下降法，通过反向传递来不断调整网络的权值和阈值，使网络的误差平方和达到期望值。BP网络为拓扑结构，其原理上就是多层感知器。因此，它的拓扑结构和多层感知器的拓扑结构相同，为层次型、前馈型结构。BP网络的学习算法就是BP算法，其核心思想是，训练过程数据包括正向传递输出过程和反馈调整过程。正向传递过程，数据依次经过输入层输入、隐含层加权及输出层输出，如果最后输出层输出数据在误差允许范围内，则训练结束，数据直接输出。反之，进入反馈调整过程。反馈调整时误差反向通过隐含层输送至输入层，输入层各神经单元均会根据反馈误差对自身神经单元权值进行修正，修正后重新进行训练，直至输出误差达到允许范围内停止反馈过程，输出层将数据输出。

激活函数的选择对神经网络构建成功与否起着关键作用，它决定了构建的神经网络拥有不同识别和分类信息的功能[23]。通过对比分析线性函数、斜面函数、阈值函数、S型函数和双极S型函数之间的差别及其所适用分析的问题发现，S型函数适用于非线性映射关系，且输出范围为0～1，与识别要求的输出范围相符合，且模型的训练和输出过程均满足要求，因此选用S型函数作为激活函数。

综上，BP神经网络三要素分别选用：非线性变换函数中的S型激活函数；层次型、前馈型网络拓扑结构；连续感知器规则的BP算法。

神经网络在训练时如果输入数据离散度很大会导致神经网络收敛速度慢、训练时间长，除此之外输出层部分激活函数是有值域限制的，例如S型函数的值域为(0，1)，双极S型函数值域为(-1，1)。因此，需要对原始输入数据进行预处理。数据预处理通常是采用归一化方法[23]。所谓数据归一化，就是将所有数据映射到[-1，1]区间或更小区间，比如[0.1，0.9]。线性转换算法是一种常用的归一化处理方法，该方法简单便捷。转换算法的表达式为

y=(x-xmin)/(xmax-xmin)

(3)

式中：y为归一化后的输出向量集合；x为输入向量集合；xmin为输入数据的最小值；xmax为输入数据最大值。

式(3)可将数据归一到[0，1]，当激活函数为S型函数时可使用该归一化方程。

1.3 动力学模型验证

选取与文献[7，26]相同或相近的参数，进行不同类型轨道不平顺激扰作用下轮轨系统动力响应仿真计算，并与文献结果进行对比，以验证模型的正确性。近似仿真计算条件下，采用本文模型计算得到的轮轨动力响应结果与文献[26]中结果的对比情况，见表1。由表1可知，采用本文仿真模型计算得到的随机不平顺激扰作用下轮轨动力响应最大值与文献中结果较为接近。随机不平顺激扰作用下轮轨垂向力响应的对比结果，见图3。由图3可知，采用本文车轨耦合动力学模型计算获得的轮轨垂向力响应无论从幅值上还是从响应曲线的变化趋势上来看，均与文献[7]较为一致。由此说明，本文所建立的高速车辆-板式无砟轨道动力学模型是可行的。

表1 仿真计算结果对比

2 离缝损伤对高速车轨系统动力响应的影响

应用上述所建立的高速车辆-CRTSⅡ型板式无砟轨道动力学模型和离缝损伤模型，分析了不同高度离缝损伤对车轨耦合系统动力响应的影响规律。通过调研发现[27]，轨道板与砂浆层间离缝脱空长度一般不大于5 m。因此，计算时，考虑较恶劣的工况，设置离缝脱空长度为5 m；车辆选用某高速动车组，行车速度为300 km/h；轨道采用CRTSⅡ型板式无砟轨道，60.64 kg/m钢轨。高速车辆和无砟轨道参数见表2、表3[7,23]。

表2 车辆模型参数

表3 轨道模型参数

不同离缝脱空高度工况下车体垂向振动加速度等动力响应指标的变化规律见图4。由图4可知，在本文仿真计算工况条件下，离缝脱空高度对车体垂向振动的影响较小；当离缝脱空高度小于1.5 mm时，高速车辆经过离缝脱空区域时，车体未出现明显的垂向异常振动；当离缝脱空高度为2.5 mm时，离缝区车体振动加速度指标出现一定的波动，但波动幅度不大。相同计算条件下，层间离缝脱空高度对轮轨垂向力和轮对垂向振动加速度两指标存在不同程度的影响。当层间离缝脱空高度为1 mm时，离缝脱空对轮轨、轮对垂向振动加速度的影响不大，两指标的最大值为78.43、26.56 m/s2，与单一随机不平顺激扰下的响应值接近；而当离缝脱空高度增加到1.5 mm时，离缝区的轮轨垂向力和轮对垂向振动加速度两指标均出现较明显的异常振动；随着离缝脱空高度的进一步增大，异常振动幅值也进一步增大(见图4(b)和图4(c))。由图4(d)可知，层间离缝脱空高度对钢轨垂向振动的影响较大，在不同高度的离缝脱空病害作用下，钢轨均出现较明显的冲击振动特征，且振动幅值随离缝脱空高度的增大而大幅增加。

图4 离缝高度对车轨耦合系统振动响应的影响

离缝脱空对轨道板和支承层振动响应也存在不同程度的影响，但其响应特征均没有钢轨振动加速度明显，限于篇幅，未一一列出其振动响应曲线。由此可见，轨道板与砂浆层间离缝损伤对钢轨垂向振动加速度的影响较为明显，可作为敏感指标用于离缝损伤识别研究。

3 砂浆层离缝损伤位置识别

应用所建立的模型，以上拱离缝损伤为例，进行了高速铁路CRTSⅡ型板式无砟轨道砂浆层离缝损伤识别研究。根据2节分析结果，选取钢轨振动加速度指标为损伤识别研究的输入对象。

3.1 损伤工况设置

分析时，损伤工况设置为横向贯通，纵向长度为5 m，离缝高度为2 mm，行车速度为300 km/h。两块轨道板之间离缝上拱损伤设置见图5，图5中阴影位置即为离缝损伤区。线路中损伤工况的设置为，取8块轨道板长度的线路，损伤设置于两块轨道板之间离缝位置。设置单损伤和双损伤工况，单损伤工况即仅有一处位置存在离缝损伤，共设置7种形式；双损工况即存在两处离缝损伤位置，同样设置了7种形式，双损工况两个损伤区域的间距分别为0、1、2、3、4、5块轨道板，损伤区域间距为3块轨道板的有两种工况。具体线路离缝损伤位置设置见图6。

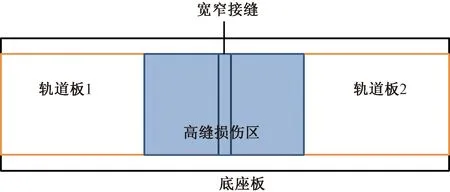
图5 轨道板离缝上拱损伤示意(俯视图)

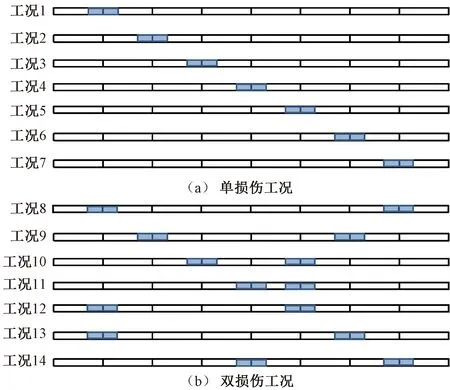
图6 线路离缝损伤工况设置

3.2 用以离缝识别的BP神经网络

根据神经网络结构的特点，要通过BP神经网络来识别离缝损伤的位置，需要从神经网络的层数、每层神经元个数、输入对象的选择、输出形式的设置及学习率等方面对BP 神经网络进行设计[23]。

(1)网络层数

理论证明[23]，具有输入层和至少一个S型隐含层以及一个线性输出层的网络，能够逼近任何有理函数；可以通过增加网络层数来降低误差、提高精度，但同时会使得网络复杂化。故选用三层神经网络，即包含输入层、隐含层和输出层。

(2)每层神经元选择

输入层和输出层神经元的选择由具体问题所决定。由仿真分析可知，钢轨垂向振动加速度指标因离缝损伤引起的响应变化最为明显，因此选择钢轨垂向振动加速度响应作为单一识别输入神经元，神经元数据节点数为7。输出层神经元选择与识别要求相关，工况共包含7个损伤位置，因此输出层神经元个数为7个。隐含层神经元的个数取决于输入层和输出层，具体计算式为

(4)

式中：m为隐含层神经元个数；n为输入层神经元个数；l为输出层神经元个数。

由式(4)计算可得，隐含层神经元不少于14个，结合训练时的收敛性和效率，初步选定隐含层神经元个数为15个。

(3)初始输入的处理及输出设定

以对损伤最为敏感的钢轨振动加速度响应作为输入，提取的数据不能直接输入，需要进行归一化处理，采用归一化处理方法将输入数据归一至[0,1]区间。还需要对归一化的数据参数化处理，增加输入数据辨识度[25]，具体过程如下。

定义损伤定位指标DSN为

(5)

式中：DS(j)为损伤指标向量第j个数值；n为选用的指标向量分量个数，本文选用神经网络n的取值为7。

为简化神经网络数据训练过程，式(5)可改为

(6)

式中：DS(j)max为集合DS(j)的最大值。

则选定的各损伤位置输入为

{输入}={DSN(1),DSN(2),…，DSN(n)}

(7)

选取离缝上拱区峰值处对称区间共500个计算步，提取此离缝区间钢轨垂向振动加速度响应作为输入，未损伤位置即提取随机不平顺作用时的钢轨垂向振动加速度响应作为输入，也是500个数值。有损和无损位置总共7个，每个位置提取500个数值。因此，一个识别线路共包含3 500个数值作为神经网络的输入。

对应位置是否存在离缝作为输出，理想情况时当该位置损伤时，该位置期望值输出数值即为1，若无损伤该位置期望值输出即为0。如工况1期望输出为：(1,0,0,0,0,0,0)T，工况12期望输出为：(1,0,0,0,1,0,0)T。7个输出值分别对应7个可能发生损伤的区域。

(4)学习速率

学习速率选取范围一般为0.01～0.8。学习速率取值过大，可能会导致系统的不稳定；而学习速率过小，又会导致系统收敛速度太慢，训练时间过长。因此，本文选取学习速率为0.1。

(5)期望误差选取

在设计网络时，期望误差值应通过训练对比之后确定一个合适的值，而这个所谓的合适的值是由隐含层的节点数决定的。通常做法是，可以同时对两个具有不同期望误差值的网络进行训练，再通过综合因素的判定最终选定其中一个。

3.3 损伤识别过程及识别结果

取工况1～工况14的所有数据及其期望输出进行训练，训练过程包含的工况越多实际计算的结果越可靠，但是增加训练样本，耗时较长，而且神经网络自适应能力较强。因此，仅对设定的14种工况进行训练。

对网络进行训练，单损伤和双损伤分别对应一个识别网络，误差取为0.001，即当网络输出值与期望值误差小于0.001即结束运算(例如期望输出为无损伤0，实际输出为0.000 5；有损伤期望输出为1，实际输出为0.999 5即视为训练满足要求)。训练过程如果不收敛则选用下一工况数据输入训练，所用工况训练结束扔不收敛，则重新开始提取数据进行循环训练。最终，单损伤工况神经识别网络迭代次数为8，双损伤神经识别网络迭代次数为11次。由此可见，随着识别要求的提高以及输出结果种类的增加，使网络收敛的训练次数也随之增多。

为区别于训练数据，重新提取线路存在损伤位置处的钢轨振动加速度响应，作为测试数据。测试训练完成后的神经网络输出能否满足要求。分别计算了单损伤7种工况和双损伤7种工况，共14种工况的实际输出。出于误差考虑，当向量数值大于0.9则视为有损伤，即为理想输出1；当向量数值小于0.1则视为无损伤，即为理想输出0。神经网络实际输出与理想输出见表4。

表4 神经网络的实际输出和理想输出

由表4可知，单损伤状态实际输出数据均在误差范围内可以按要求近似为0或者1，无超出误差范围的异常值，均可近似为理想输出，即训练达到了要求。双损伤状态实际输出数据虽然与期望输出间的误差有所增加，个别数据浮动较大，但是仍在误差要求范围内，可近似为0或者1。

进一步对比表4发现，单损伤工况下有损伤位置的神经网络实际输出平均值为0.997，无损伤位置神经网络输出平均值为0.001 6；双损伤工况条件下，有损伤位置的神经网络实际输出平均值为0.994，无损伤位置神经网络实际输出平均值为0.004。从系统输出平均值来看，实际输出与期望输出存在一定的误差，但误差很小。无损伤区域和损伤区域有明显的辨识度。双损伤工况下BP神经识别网络实际输出误差较单损伤工况下的输出误差要大。

当理想输出为0时，即该位置轨道结构状态良好；当输出为1时，即该位置轨道结构状态发生离缝损伤。统计出14种工况下的理想输出见表5。由表5可知，输出为1的位置与损伤设置位置完全吻合。由此说明，以钢轨垂向振动加速度响应为输入的BP神经网络可以很好地识别离缝损伤的具体位置。

表5 神经网络的近似理想输出

综上可见，以参数化处理的钢轨垂向振动加速度响应作为BP神经网络识别系统的输入，可以识别离缝损伤位置及损伤与否，在误差允许范围内对离缝损伤与否的识别率达到了100%，识别系统能精准判别损伤位置且判别正确率达到了100%。双损伤状态需要判断的可能性增加，系统更加复杂。因此，实际输出相比于单损伤状态实际输出误差更大，但是二者输出均在误差允许范围之内。

4 砂浆层离缝损伤程度识别

3节对离缝损伤位置进行了识别研究，由输出的结果可以看出，所建立的BP神经网络可以对离缝损伤与否及离缝损伤位置进行有效判别。本节基于上节的BP神经网络设计算法，进一步对离缝损伤程度进行识别研究。

分析时，离缝损伤工况设置为横向贯通，纵向长度为5 m，离缝高度分别设置为0.5、1.5、2.5 mm三种。两块板之间的离缝上拱损伤区域设置与图5相同。线路中损伤工况的设置见图7，为与前文中工况相区别，该工况记为工况I，取8块轨道板长度的线路，损伤设置于两块轨道板之间离缝位置处。

图7 线路损伤工况设置

提取线路可能损伤位置处的钢轨振动加速度响应作为测试数据，测试训练完成后的神经网络输出能否满足要求。分别计算图7所示工况的实际输出，为防止偶然性的出现，共计算了3次，输出为7维列向量，输出值保留3位有效数字。神经网络实际输出与理想输出结果见表6。

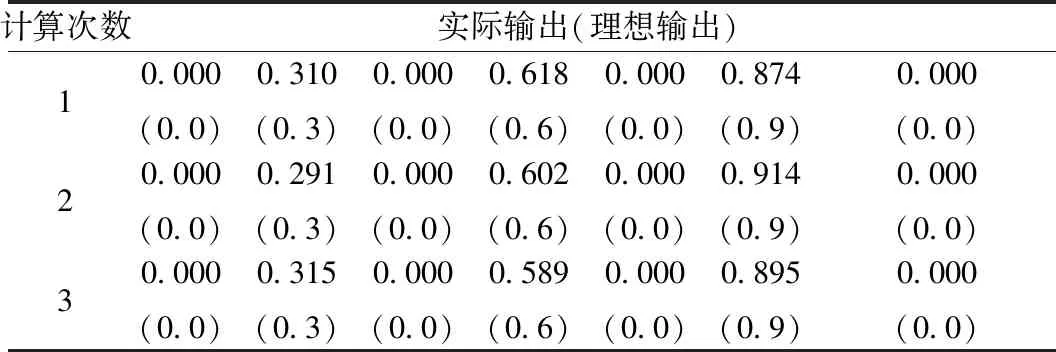
表6 不同损伤程度神经网络的实际输出和理想输出

出于误差考虑，当列向量实际输出数值与理想值之间的差值在±0.05范围内时即视为有效输出，能识别损伤程度。从表6实际输出数值与理想输出数值之间的对比可以看出，所有的输出数值均在误差允许范围内。无损伤位置处实际输出平均值为0；离缝高度为0.5 mm处实际输出平均值为0.305，与理想输出间的误差为0.005；离缝高度为1.5 mm时，实际输出平均值为0.603，与理想输出结果间的误差为0.005；而离缝高度为2.5 mm时，实际输出平均值为0.094，与理想输出间的误差为0.006。由此可见，实际输出与理想输出之间误差并不大，不同损伤状态对应的输出数据有良好的辨识度。

综上所述，以参数化处理的钢轨垂向振动加速度响应作为BP神经网络识别系统的输入，在经过一定次数的训练后，可以精确的定位到损伤位置，并对离缝损伤程度进行较好的识别。但是，相对于判断单一的离缝损伤存在与否，基于BP神经网络系统进行离缝损伤的程度识别时，其训练过程要复杂得多。

5 结论

建立了包含砂浆层离缝损伤的高速车辆-板式无砟轨道耦合动力学模型，分析了对离缝损伤较为敏感的车轨系统动力学响应指标，在此基础上，通过构建BP神经网络模型，以离缝上拱损伤为例，进行了砂浆层离缝损伤识别研究。主要研究结论如下。

(1)钢轨垂向振动加速度响应指标对砂浆层离缝损伤较为敏感。以参数化处理的钢轨垂向振动加速度响应作为BP神经识别网络的单输入，来判断砂浆层是否存在离缝损伤、离缝损伤的位置以及判断离缝程度的识别方法是可行的。

(2)BP神经网络对单损伤状态和双损伤状态均能进行有效识别。但是双损伤状态训练时要迭代至误差允许范围需要更多的训练次数。由此说明损伤的状况越复杂，可能性越多，识别网络训练过程越复杂，所需的训练迭代次数也就越多。

(3)双损伤状态需要判断的可能性增加，系统更加复杂。因此，实际输出相比于单损伤状态实际输出误差要大，但是二者输出均在误差允许范围之内。