基于非线性理论的接触网找形方法研究
罗 群,梅桂明,赵 晨,王江文,邱江洋,韩宝峰
(1.西南交通大学 牵引动力国家重点实验室,四川 成都 610031;2.广东交通职业技术学院,广东 广州 510650;3.中车青岛四方机车车辆研究所 重庆研发中心,重庆 401133;4.保德利电气设备有限责任公司,陕西 宝鸡 721000)
高速列车通过车顶受电弓与接触网稳定接触以获取电能,进行电力牵引,其运行性能很大程度上取决于受电弓与接触网之间的动态相互作用[1-2]。而深入开展受电弓与接触网动态相互作用的仿真计算研究,对高速列车运行性能的提升有着重要作用[3]。近年来,针对这一课题,建立了不同的仿真计算模型用来模拟受电弓与接触网的动态相互作用关系,其建模方法主要分为两种:基于绝对节点坐标法(ANCF)的有限元方法[4-7]以及空间有限元法[8-10]。但无论是仿真模型还是建模方法的选择,接触网系统的初始平衡构型将会对仿真结果产生极大的影响[11-12]。因此,仿真前准确获得接触网系统的初始平衡构型显得尤为重要。
通过坐标系描述的接触网系统几何形貌称为接触网构型[13],接触网系统在其自身重力、张力体系以及边界条件的约束下将形成预设弛度的内应力平衡的初始构型[14],而确定这一满足平衡的初始构型的过程,称为找形[13]。目前,找形中使用较多的分析方法为非线性位移法[15]和力密度法[16]。非线性位移法即在所求结构的几何变化的基础上,寻找达到规定力分布的平衡构型。该方法从初始力分布、悬索之间的连续性以及边界条件,获得初始应力构型和内应力分布。而力密度法,则是通过规定力密度,将悬索节点坐标的非线性平衡方程转换为线性方程组。
在上述分析方法的基础上,国内外学者提出了多种具体的接触网找形方法。文献[4]提出利于求解悬索等大变形结构的ANCF方法进行接触网找形,其考虑了接触网两节点有限元单元的轴向和弯曲变形,并通过分段方程控制张力。文献[12]提出悬链线方程找形法,通过悬链线一般表达式,建立接触网整体力平衡式求解其初始构型。文献[17]采用抛物线找形,将接触网离散为抛物线单元,建立承力索力矩平衡方程式求解承力索初始构型。文献[9]采用有限元法找形,使用欧拉-伯努利梁单元离散接触网,通过吊弦张力的最小误差确定吊弦长度,最终得到接触网的初始平衡构型。
对比上述方法,ANCF法找形结果虽然具有良好的计算精度,但单元数较多且涉及高阶导数的运算,有限元法单元数也较多,求解规模均较大;对于抛物线法找形,计算过程中只考虑其线性项而忽略了非线性项,导致跨中部分吊弦长度计算结果相对误差较大;而悬链线方程找形方法,其基于非线性理论,充分考虑了计算过程的非线性项,能够准确表示吊弦与吊弦间的接触网单元,且该方法求解规模取决于吊弦数量与控制张力数量,求解规模小,即该方法同时具有计算精度高、求解快速等优点。因此,本文将使用非线性理论下的悬链线方程计算获取接触网初始平衡构型。与文献[12]不同地是,本文将使用悬链线方程的精确解析式,并结合分模法[18]的思想进行接触网找形,即先分离求得接触线初始平衡构型,再基于悬链线方程和初始构型下的单元节点力平衡关系得到承力索、弹性吊索等结构的初始平衡构型,在保证计算精度的同时,简化了求解形式并降低了求解规模。
1 非线性基本理论
缆索的受力计算理论主要有线性理论和非线性理论,其中线性理论假定垂向载荷沿着索跨度均布,推导得到抛物线方程,而非线性理论假定垂向载荷沿着索长度均匀分布,推导得到悬链线方程,同时,在推导过程中假设缆索为理想柔性且其材料符合胡克定律[19]。
高速铁路接触网系统中接触线、承力索以及弹性吊索均为缆索结构,重力荷载沿索长均匀分布,弯曲刚度可忽略,与非线性理论相契合。同时,文献[20]也验证了悬链线单元对含有初始弯曲的电缆建模的可靠性以及实用性。因此,可将非线性理论应用于接触网找形,并通过悬链线方程表示离散的接触网悬链线单元,其中包括了不等高与等高悬链线方程。
不等高悬索计算简图见图1。图1(a)表示荷载q沿索长均匀分布且两端分别悬挂于AB两点的不等高悬索,AB两点间距为L,高度为h,索两端张力分别为T1、T2,其分量为T1x、T1y、T2x、T2y。该悬索的任意微分单元dx受力分析见图1(b),Tx为索张力的水平分量。
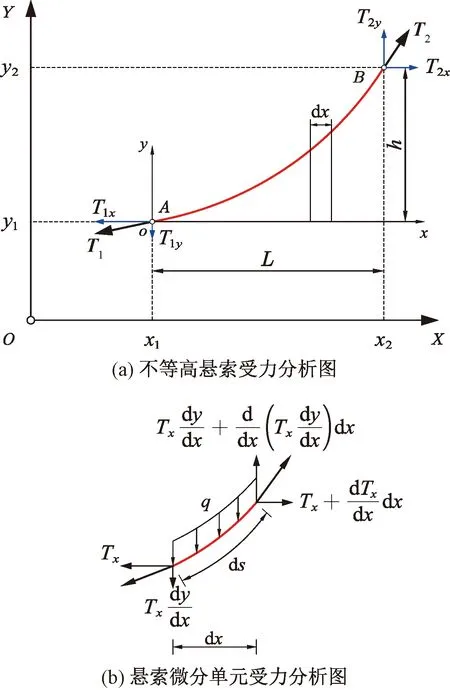
图1 不等高悬索计算简图
根据微分单元的静力平衡条件,有
( 1 )
式( 1 )可化简为
( 2 )
式中:Tx为恒定值,并进一步的可以得到
( 3 )
求解式( 3 )可以得到坐标系oxy中悬索AB的悬链线方程。满足边界条件的解为
( 4 )
式中:D1、D2为由其余参数计算得到的常数项;C为常数,计算式为
( 5 )
同时,为便于描述各接触网单元,并根据A、B两端点坐标值,D1、D2又可分别定义为
( 6 )
D2=-C·coshD1
( 7 )
式中:ρ为索的线密度;g为重力加速度;(x1,y1)、(x2,y2)分别为A、B两点坐标。
注意到式( 4 )为坐标系oxy中的悬链线方程,通过坐标转换可得到全局坐标系OXY中的悬链线方程为
( 8 )
式( 8 )即为全局坐标系下,表示悬索AB在重力荷载沿索长分布作用下的不等高悬链线方程。
当A、B两端点等高时,y1=y2,代入式( 6 )有
( 9 )
将式( 9 )代入式( 8 )则可得等高悬链线方程。
2 接触网找形研究
2.1 接触网模型
接触网系统的悬挂导线主要由接触线、承力索以及吊弦组成,我国高速铁路常用的两种结构[21]见图2。图2(a)为简单链型悬挂接触网,主要结构为承力索、接触线和吊弦,长度不等的吊弦通过线夹将承力索与接触线进行连接。与简单链型悬挂接触网相比,弹性链型悬挂接触网则在承力索的两跨之间增加了结构弹性吊索,见图2(b)。

图2 简单链型、弹性链型悬挂接触网示意
本文将使用基于非线性理论的悬链线单元对接触线、承力索以及弹性吊索进行离散,以吊弦数为nd的单跨弹性链型悬挂接触网为例,将相邻吊弦间、吊弦与定位点间的承力索、接触线以及弹性吊索均离散为悬链线单元,则对应单元总数N=2(nd+1)+4。
此时考虑左右各2个弹性吊索悬链线单元,若计算多跨则应减去重复计算的单元数。而对于简单链型悬挂接触网,减去弹性吊索的悬链线单元数即可。
2.2 接触网找形流程
本文使用非线性理论对接触网进行找形,流程见图3。由于接触网在铺架的过程中,吊弦数量以及接触线的初始构型具有预设条件,即接触线的各节点坐标参数已知。根据此结构特点,将接触网离散为悬链线单元后,先分离并求解接触线平衡构型,并计算出各节点的吊弦力;然后整体求解承力索、弹性吊索和吊弦的平衡构型,利用悬链线方程式( 8 )初步表示平衡构型下各结构的悬链线单元,并确定其中未知参数数量Nx,通过吊弦力平衡关系以及承力索、弹性吊索端部张力平衡关系,建立求解未知参数方程组;最后根据方程组的非线性,使用牛顿-拉夫森法迭代求解。解出未知参数后,进一步可得到初始平衡构型下承力索和弹性吊索各悬链线单元解析式,从而完成接触网找形。

图3 接触网找形流程
2.3 接触网找形理论
以弹性链型悬挂接触网为例进行接触网找形计算,其主要结构为接触线、承力索、弹性吊索以及吊弦。含有吊弦数为nd的弹性链型悬挂接触网分析示意图见图4,采用下标cw、sw、ms、mw分别表示与接触线、弹性吊索、弹性吊索上方承力索部分(A′C、DA″段)、承力索中间部分(CD段)的相关参数,如Tcw、Tsw、Tms、Tmw表示接触线、弹性吊索、弹性吊索上方承力索部分、承力索中间部分的控制张力。需要注意地是,由于存在弹性吊索,一跨内的承力索控制张力不再相等,此时,设计要求的承力索张力Tmw控制在图4中CD段,而A′C、DA″段的控制张力Tms则需根据力平衡关系求解出。

图4 弹性链型悬挂接触网分析

2.3.1 接触线计算
将接触网系统离散为悬链线单元后,先对接触线的初始平衡构型进行计算。其中,接触线的定位点与节点、节点与节点间均离散为悬链线单元,由式( 8 )可得各单元方程为
k=0,1,2,…,nd
(10)

(11)



(12)
(13)
表示出接触线的悬链线方程组后即确定了接触线的初始平衡构型。此时,还需求出接触线对吊弦的作用力,为承力索、弹性吊索和吊弦的求解做准备。接触线对第i吊弦作用力可表示为
(14)

(15)
2.3.2 承力索、弹性吊索与吊弦整体计算
弹性吊索上方承力索部分(A′C、DA″段)、承力索中间部分(CD段)、弹性吊索的控制张力不同,但每部分的水平张力为恒定值,可以分别对其建立悬链线单元方程。弹性吊索的B′B、EE′对应的悬链线单元分布在两跨之间,在对单跨模型找形时将其考虑在内,即单跨模型考虑左右各2个弹性吊索悬链线单元。
通过式( 8 )分别建立承力索、弹性吊索的悬链线单元方程为
k=1,2,…,nd-1
(16)
k=0,nd
(17)
n=1,2,4,5
(18)

同时,Cmw、Cms以及Csw可表示为
(19)

连接承力索和接触线的nd-2个吊弦力平衡方程、连接弹性吊索和接触线的2个吊弦力平衡方程分别为
i=jj=2,…,nd-1
(20)

i=1,ndn=1,4
(21)

(22)
(23)
式(20)可由式(14)求得,表达式为
(24)
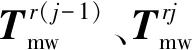
(25)
式(21)中其求解形式与式(14)、式(24)一致,即
(26)
其中
(27)
接着,建立承力索以及吊弦端部张力平衡方程为
(28)
(29)
(30)
以上已建立方程数为nd+3,还需补充3个方程才能求解。承力索单元A′C的端部张力Tms未知,点C为连接三部分的节点,对点C建立力平衡方程可得
(31)

(32)
注意到节点D也为承力索与弹性吊索的连接点,建立节点D垂向力平衡方程为
(33)

联合式(20)~式(33)可以建立含有Nx个方程的非线性方程组,采用牛顿-拉夫森法对该非线性方程组进行求解,可将其未知数全部求解出,即将承力索与弹性吊索的初始平衡构型以及吊弦长度求解出。至此,弹性链型悬挂接触网的找形计算全部完成。
对于简单链型悬挂接触网,见图2,承力索的定位点下方未设有弹性吊索。此时,Tms=Tmw,即整根承力索控制张力为恒定值,同样可以通过上述弹性链型悬挂接触网找形计算过程完成接触网找形。
2.3.3 迭代算法
由于牛顿-拉夫森迭代法具有收敛的快速性和准确性等优点[22],本文将使用该方法对2.3.2节组建的非线性方程组进行求解,求解流程见图5。

图5 非线性方程组求解流程
设置未知参数的迭代初值,组成初值矩阵X;将对应初值代入各方程中组建非线性方程组F=0;计算出Jacobi矩阵J,并由H=-J-1F得出校正矩阵H;判断校正矩阵H的二范数是否满足预设条件,若不满足,则使用校正后矩阵X=X+H再次计算,若满足,则输出矩阵X。此时,输出的X为未知参数的数值解,将其代入式(16)~式(18)中可将承力索、弹性吊索以及吊弦的平衡构型表示出,即完成接触网的找形。
3 模型验证
上述方法将用于不同接触网模型的找形,确定模型的初始平衡构型。接触网的找形结果可通过吊弦的长度以及接触线的平衡构型来评估[23],因此,将算例相关计算结果与标准或已发表文献中相同边界条件的模型结果进行对比,用于验证本文找形方法的准确性、有效性和工程实用性。
3.1 简单链型悬挂接触网模型
模型1选择欧洲标准EN 50318—2018中简单链型悬挂接触网的参考模型[23],该模型参数用于检查接触网的新生产线是否合格,也可用于对仿真模型的初步检查。文献[3]中将该模型用于现有10家机构开发使用的不同模拟软件找形结果对比。该接触网模型的几何参数见表1,该接触网模型的物理参数见表2。

表1 模型1接触网几何参数

表2 模型1接触网物理参数
本文方法得到的模型1接触网模型初始平衡构型见图6。将计算所得吊弦长度与标准对比,结果见表3,由于该模型具有对称性,只将前5吊弦进行对比,由表3可知,吊弦长度结果与标准值非常接近,最大相对误差为0.34%,说明了本文找形方法的准确性。

图6 简单链型悬挂接触网模型初始平衡构型

表3 吊弦长度计算结果对比
同时,对找形结果中接触线初始构型进行评估。文献[3]中各家机构由于边界条件考虑不一致,其所得的接触线初始构型虽存在差异,但结果基本一致。将本文找形方法所求构型与其中一家机构PACDIN[24]的计算结果进行对比,见图7。将吊弦力与该机构计算结果进行对比,见表4,虽然结果存在一定差异,但最大相对误差为1.720%,未超过2%,可认为利用本文方法找形结果正确,且准确性好。

图7 接触线初始构型对比

表4 吊弦力计算结果对比
3.2 京津城际铁路接触网模型
模型2实际设计京津城际铁路接触网模型,文献[17]根据京津线设计要求通过抛物线找形法完成标准跨距接触网的找形,本文将使用文献中相关参数进行找形计算,验证本文计算方法的精确性。模型2的几何参数见表5,物理参数见表6。

表5 模型2接触网几何参数

表6 模型2接触网物理参数
京津线接触网单跨模型找形结果见图8,提取吊弦长度以及吊弦力等相关参数与文献[17]参考值进行对比,见表7。

图8 京津城际铁路接触网模型初始平衡构型

表7 吊弦长度及吊弦力计算结果对比
从表7中可以看出,在吊弦力计算方面,本文计算结果与文献[17]的计算值、仿真值基本一致;而在吊弦长度上,本文计算结果较文献[17]的计算值更接近于其仿真值,最大相对误差仅为0.4%,即本文方法较抛物线找形法能够更精准地计算接触网模型吊弦长度。
3.3 弹性链型悬挂接触网模型
模型3选择标准EN 50318—2018中弹性链型悬挂接触网的实测线路模型[23],对该接触网模型中锚段关节进行找形,与前几个算例不同地是,本算例接触网模型带有坡度,且含有弹性链型悬挂接触网、过渡跨以及简单链型悬挂接触网等常用接触网模型,具有代表性。该接触网模型的几何参数见表8,该接触网模型的物理参数见表9。

表8 模型3接触网几何参数

表9 模型3接触网物理参数
通过本文方法对接触网模型3进行找形,所得到的接触网初始平衡构型见图9。由于本模型第一跨为无预弛度的弹性链型悬挂接触网,第二跨(锚段关节过渡跨)中,左侧含有弹性吊索而右侧为简单链型,且整垮具有一定坡度,涵盖了现有接触网不同结构、边界条件。因此,提取第一、二跨吊弦长度计算结果与标准EN 50318—2018中实测数据对比,其结果见表10、表11。

图9 接触网锚段关节处初始平衡构型

表10 模型3第一跨吊弦长度计算结果对比

表11 模型3第二跨吊弦长度计算结果对比
通过以上对比可知,本文计算结果与标准实测值非常接近,最大相对误差仅为0.668%,说明了本文方法找形结果准确性好,且证明了方法的工程实用性。
4 结论
本文进行了一种基于非线性理论的接触网找形方法研究,并以弹性链型悬挂接触网为例建立了接触网求解模型。将接触网相邻吊弦间、吊弦与定位点间的承力索、接触线以及弹性吊索均离散为基于非线性理论的悬链线单元后,先分离求解接触线初始构型;再通过力平衡关系搭建用于求解承力索、弹性吊索以及吊弦平衡构型的非线性方程组,其中包括吊弦力平衡关系以及结构控制张力平衡关系;最后使用牛顿-拉夫森迭代法求解,得到接触网初始平衡构型,从而完成找形。通过三个算例验证,得出以下结论:
(1)接触网找形过程的求解规模取决于吊弦数量与控制张力数量,求解规模相对较小,并能快速求解。
(2)对欧洲标准EN 50318—2018中简单链型悬挂接触网的参考模型进行找形计算,结果对比表明,吊弦长度的计算结果与标准值对比,最大仅相差0.34%。接触线初始平衡构型与某机构找形结果具有良好的一致性,所得吊弦力与其最大相差1.720%,满足工程应用要求,证明了本文找形方法的准确性和有效性。
(3)对京津城际铁路接触网标准跨进行找形计算,结果与文献结果对比显示,吊弦力计算基本一致,而吊弦长度计算更接近文献仿真计算值,验证了本文找形方法的精确性。
(4)对欧洲标准EN 50318—2018中弹性链型悬挂接触网的实测线路模型进行找形计算,结果对比显示,吊弦长度的计算结果与标准值对比,最大仅相差0.668%,验证了本文找形方法的工程实用性。
(5)已实现对简单链型、弹性链型、锚段关节等接触网模型找形,也适用于其他类型、不同边界条件的接触网找形。同时,找形结果可作为初始条件用于受电弓与接触网的动态仿真计算,也可为实际线路的接触网设计提供参考。

