列控车载设备现场测试案例执行距离估算方法研究
张亚东,袁榆淞,饶 畅,郭 进
(1.西南交通大学 信息科学与技术学院,四川 成都 611756;2.重庆交通大学 交通运输学院,重庆 400074)
CTCS-2级列控系统是基于轨道电路和点式信息设备传输行车许可的列车运行控制系统,由地面设备和车载设备组成,其中车载设备是对列车速度进行防护的重要设备。为保障行车安全,车载设备在投入运营前必须进行一系列严格的测试。按照测试阶段的不同,可分为实验室仿真测试、现场测试、互联互通测试和联调联试等[1]。
车载设备的现场测试通常是一个动态、连续的过程,对应的测试案例数量庞大。为了缩短测试周期,提高测试效率,通常会将若干个测试案例按照一定原则有序串接形成测试序列连续执行。近年来,国内外研究人员围绕测试序列的合理高效串接问题进行了大量研究。张勇等[2]基于图论方法,以车载设备运行模式为框架,采用中国邮路问题的求解思路寻求测试序列的优化串接方法。赵晓宇等[3]针对测试序列串接过程中的算法搜索死循环和状态空间爆炸问题,提出了一种基于有色Petri网的测试序列生成方法。ZHENG等[4]为降低测试序列对于测试案例的重复覆盖程度,提出了一种基于全路径覆盖的测试序列优化选择算法。
上述研究主要解决实验室仿真测试阶段的测试序列串接问题。与实验室仿真测试不同,在现场测试阶段,串接测试序列还需进一步考虑实际线路条件约束,从而确保测试案例在符合条件的线路区段得以执行。合理估计测试案例的执行距离,是串接现场测试序列的关键之一。现有估计测试案例执行距离的相关研究主要依赖于人工经验,将现场测试案例的执行距离粗略划定为某个固定长度。袁磊等[5]选定线路上相邻间距大于500 m的应答器组位置作为测试案例的布置点,从而将相邻布置点的距离估计为测试案例的执行距离。李彬[6]将线路上长度大于200 m的计轴区段划定为测试区段用于布置测试案例,从而把测试区段的长度估计为测试案例的执行距离。类似的还有李智[7]等提出的方法等。然而,现场测试案例的执行距离受执行步骤数量、操作类型、线路条件、列车运行模式、动力学状态等多种因素影响,往往会发生动态变化。现有方法未能充分考虑这些因素,因而容易出现执行距离长度划分不合理的情况,导致列车在测试过程中发生空跑,甚至无法在规定区段内执行完测试案例,进而造成测试中断、测试过程能耗大、成本高等问题。
针对上述问题,本文提出一种基于列车动力学模型的现场测试案例执行距离估算方法,通过建模描述列车在现场测试过程中的动力学状态变化情况,采用列车动力学分析方法,综合考虑线路条件、司机反应时间、操作类型等因素影响,计算列车在各动力学状态下的运行速度、位置变化规律,近似估计列车执行该测试案例的走行距离。然后基于实验室测试平台对案例进行测试执行验证,以对本文提出的方法进行检验。
1 车载设备现场测试过程
车载设备的现场测试通常以相关技术规范为依据[8],通过安排列车在现场实际线路上运行,对车载设备应答器信息接收、动态曲线计算、速度监控、最限制速度曲线计算等功能特性进行测试,覆盖站内接发车、区间追踪、自动过分相、模式转换等运营场景。现场测试案例可由专家经验[9]或软件测试理论方法[10]构造得到,通常具备一定的执行距离,测试人员通过人机界面(DMI)、记录单元(JRU)等接口观察测试过程中车载设备的状态变化和预期输出。
测试案例1:“在完全监控模式下,列车接收到【CTCS-5】绝对停车信息包,应触发紧急制动直至停车”。
如图1所示,测试案例1开始执行时,列车以速度vA处于A点,DMI图标显示当前模式为“完全”;列车保持匀速前行,到达B点,此时列车速度vB=vA,车载设备接收并解析地面应答器发送的【CTCS-5】绝对停车信息,DMI速度指针及环形光带显示为红色,并验证输出紧急制动;列车在紧急制动状态下降速运行,直至在C点处停车,此时列车速度vC=0;DMI给出允许缓解语音提示后,测试人员按压缓解按钮,缓解制动,至此测试案例1执行结束,列车运行至下一条测试案例的执行范围内。

图1 现场测试过程举例1
由图1可见,该测试案例的实际执行距离为AC段。然而,如果对测试案例的预估执行距离出现较大偏差,比如执行距离被预估为AD段,则会造成列车在CD段的空跑,由此将带来测试成本升高、测试效率降低等问题。反之,若实际执行距离大于了预估的执行距离,且测试序列串接时对案例执行距离的误差余量选取不合理,则可能造成当前测试案例的执行范围侵占到下一条测试案例的执行范围,直接导致下一条测试案例无法在规定的线路条件下执行,进而导致现场测试序列发生中断。因此,合理估计测试案例的实际执行距离,不仅有助于缩短测试过程中列车的空跑距离,而且可以避免发生测试中断,从而有利于高效合理地串接现场测试序列,降低现场测试能耗和成本,提高测试效率。
2 测试过程状态模型
测试案例的执行距离与案例的执行步骤数量、操作类型、线路条件等密切相关,且不同测试案例的执行步骤往往具有较大的差异,这给直接计算测试案例的执行距离带来了巨大困难。然而,本文注意到列车的动力学状态变化是贯穿整个测试执行过程最显著的特征,也是影响测试案例执行距离的关键内在因素。因此,本文从该特征入手,提出以列车动力学状态作为纽带,对不同测试案例的执行过程进行统一、抽象化的描述,从而为估算测试案例的执行距离提供依据。
2.1 模型构建
由于列车执行现场测试案例是一个连续且动态的运行过程,因此本文把列车在执行测试案例过程中所有可能出现的动力学状态抽象为点的集合,状态之间的变化关系抽象为边的集合,从而构建出车载设备测试过程的有向图模型G=(S,E)。其中,S为列车运行状态的顶点集合,S={S0,S1,S2,S3,S4,S5,S6,S7};E为列车运行状态变化关系的有向弧集合,E={e1,e2,…,e31};测试案例的执行过程则是有向图模型G中顶点S0到顶点S7的某一条路径。车载设备测试案例执行过程的有向图模型见图2,图2中各顶点变量的含义见表1。

图2 车载设备测试案例执行过程的有向图模型

表1 模型中顶点变量的含义
对于测试案例1,根据列车的动力学状态变化情况,列车分别依次经历了巡航状态、紧急制动状态和停车状态,其测试执行过程的有向图路径可以表示为S0→S2→S5→S6→S7。注意,本文将S0、S7两个状态定义为标志测试案例开始执行和执行结束的抽象状态,对应的走行距离规定为0。此外,执行测试案例的不同步骤可能造成列车动力学状态反复发生多次变化,因此路径中的顶点可能会重复出现。例如在某次测试中,列车分别依次经历了巡航状态、紧急制动状态、停车状态、牵引状态、巡航状态和牵引状态,其有向图路径表示为S0→S2→S5→S6→S1→S2→S1→S7,此时顶点S1、S2各重复出现2次。
测试过程模型刻画的是不同测试案例执行过程中的列车动力学状态宏观演变情况,而测试案例之间的微观差异,如执行步骤与数量、操作类型、所需线路条件等,将在后续计算案例的执行距离时做进一步考虑。
2.2 相关定义
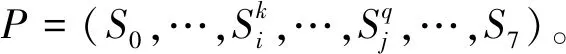


规定列车在两个相邻动力学状态变化中,后一状态的入口速度等于前一状态的出口速度。

在测试案例的某些执行步骤中,通常会明确地或隐含地给出列车运行的部分距离,这些给定的距离将会影响到测试案例的执行距离估算,相关定义和说明如下。
定义4固有距离:测试案例执行步骤中明确给出的运行距离,记作Lg。按照距离的直观性可分为显式固有距离和隐式固有距离。
定义5显式固有距离:测试案例执行步骤中以数值的形式直接给出的距离信息,记作Lgx。例如测试案例步骤中描述了“列车运行50 m后,收到应答器报文”,那么Lgx=50 m。
定义6隐式固有距离:测试案例执行步骤中未以数值形式给出距离长度,但是可以根据涉及到的特殊运营场景,查阅车辆参数或线路数据等确定的运行距离,包括车长、分相区长度、等级转换中预告点与执行点之间的距离等,记作Lgy。

测试案例2:“列车以速度100 km/h运行,200 m后运行至应答器组A处,接收到【ETCS-5】应答器链接包,给出下一个被链接的应答器组编号为2,列车运行到下一被链接的应答器组B,读取应答器编号为3,与链接信息不符,车载执行链接反应输出紧急制动”。

3 测试案例执行距离估算方法
3.1 方法框架

输入:车辆参数、线路数据、测试执行过程的有向图路径P、测试案例执行步骤、固有距离Lg。
输出:测试案例执行距离L。
开始
初始化L←0
for(intk=2 to ∣P∣-1) 执行

continue
else

end if
end for
L←L+Lg
returnL
结束
该方法主要包括如下步骤:
Step1获取车辆参数(包括车长、车重、牵引特性曲线、目标制动减速度等)和测试区段的线路数据(包括线路坡度、曲线半径、线路限速、特殊区段位置等),并根据测试执行步骤构建测试执行过程的有向图路径P。


Step4所得结果与固有距离Lg相加,输出测试案例执行距离。
3.2 距离计算

表2中:a牵n为第n步牵引加速度,m/s2;vn为第n步速度,m/s;dn为第n步的位置,m;Δt为单位时间步长,设置为0.5 s;t2为列车在巡航状态下的运行时间;L分相区为线路数据提供的分相区长度,m;L断为列车断开主闸时距离分相区起点的距离,m;L合为列车驶出分相区后到合上主闸的走行距离,一般取值为130 m;t断为输出过分相命令信号时车头距分相区起点的时间,一般取值为10 s;v触为列车触发制动的速度,m/s;t空为列车空走时间,s;v缓为允许缓解速度,m/s;a制n为第n步常用制动加速度,m/s2。

表2 不同状态下测试执行距离计算方法
对于巡航时间t2,通过分析具体的测试步骤可知,t2主要取决于测试过程中测试人员人工操作设备、观察或记录所花费的时间。本文根据现场测试过程的操作步骤及其复杂度依托列控车载设备测试平台[11]进行了多次模拟试验,将不同类型的操作步骤及其所花费时间进行了统计分析,见表3。
对于追加的补偿距离,在人控优先方式下,触发常用制动后,从DMI给出允许缓解指示到司机按压缓解按钮,再到车载设备取消制动,这一过程存在延时,使得列车在常规制动状态的出口速度低于规定的允许缓解速度,故需再加上补偿距离才能计算得到列车在该状态的测试执行距离。进行计算时,延时可由表3确定为4.5 s,并以允许缓解速度作为初速度,采用分段迭代法进行制动计算,所得的列车运行距离增量即为补偿距离,速度即为出口速度。

表3 测试人员的操作类型及其期望花费时间
4 试验验证
4.1 算例分析
以过分相场景类中的F510000-TC01案例作为示例,对本文方法进行应用验证。其中F510000代表功能特征号为510000(过分相功能),TC01代表测试案例编号为01。车辆参数选用8节车辆编组的CRH2型列车参数,并假设列车处于平直无坡道的线路上运行。
测试目标:列车接收到应答器过分相预告信息,验证车载设备实现自动过分相控制。F510000-TC01的主要测试步骤见表4。

表4 F510000-TC01主要测试步骤
如图3所示,列车在A点处开始执行测试案例,测试人员验证DMI显示当前模式为“完全”,调整列车速度vA=100 km/h;列车运行L1(200 m)后,到达B点,列车收到【ETCS-68】包,测试人员检验DMI输出分相区预告图标,TIU输出过分相选择信号;列车继续运行L2到达C点,此时车头距分相区起点约10 s,测试人员验证DMI输出两遍“前方过分相”语音提示,TIU输出过分相命令信号,列车断开主闸,进入惰行状态;保持列车自动过分相,列车驶出分相区后一定距离到达F点,测试人员验证TIU撤销过分相命令信号,列车合上主闸,恢复牵引,进入巡航状态;列车继续向前运行至G点(距离分相区终点约600 m),测试人员检查TIU停止输出过分相选择信号及JRU相关信息包的记录,在验证过程中,列车继续向前运行距离L4,到达H点,测试案例执行结束。

图3 测试案例执行过程分析

4.2 有效性评估
为进一步验证本文方法的有效性,采用随机抽样方法,以技术规范所定义的功能特征为划分,从现场测试案例库中选取测试案例进行执行距离估算。所选取的测试案例涵盖了应答器报文接收、动态速度曲线计算、速度监控、速度与距离计算、最限制速度曲线计算、轨道电路信息接收和使用等规定的功能特征,覆盖列车自动过分相、等级转换、模式转换、调车作业等规定的运营场景。本文采用实验室车载测试平台对所选测试案例进行实际执行和对比分析。其中,线路条件取坡度为0‰的平直轨道,线路限速为200 km/h,车辆参数为CRH2型动车组标准参数[12]。本文方法估算的距离与实际执行距离对照情况见表5。

表5 本文方法估算的距离与实际执行距离对照情况 m
从表5可以看出,以实际执行距离作为参考标准,本文估算结果与实际执行距离之间的误差绝对值控制在了50 m以内,体现出本文所提方法具备有效性。在此基础上,本文从方法的估计误差粒度入手,与现场测试的各种最不利指标进行比对,从而对本文方法的有效性进行进一步分析。
具体地,现场测试通常涉及到长度/距离等特征的元素包括轨道区段长度、列车长度、列车紧急制动和常用制动距离等,取本文实验相同的CRH2型动车组标准参数,按现场测试的最不利条件[13],以列车最限制速度40 km/h、线路坡度为上坡35‰对现场特征元素涉及的长度/距离等进行分析计算,本方法的估计误差粒度与各特征元素的长度/距离比较见表6。

表6 本方法的估计误差粒度与各种特征元素的长度/距离比较
分析表6可知,站内轨道区段长度是最严苛的现场测试特征元素,取值为60 m。在进行现场测试序列串接过程中,为保证测试的连续性,通常会预留一定距离作为误差余量的阈值。而本方法的估计误差粒度小于站内轨道区段长度(占比约83.33%),意味着本文方法产生的结果误差控制在了最严苛特征元素的取值范围内,为合理选取误差余量的阈值提供了依据,从而有利于在现场测试序列串接中控制其他变量因素(例如压缩列车空跑距离),提高测试效率。
5 结论
本文围绕列控系统车载设备现场测试案例的执行距离估计问题,提出一种基于列车动力学模型的现场测试案例执行距离估算方法。从动力学的角度对现场测试案例的执行过程进行建模,将复杂的测试案例执行步骤抽象为有向图路径,采用动力学分析计算得到案例的执行距离。在平直轨道、线路限速为200 km/h的试验工况下,本方法对现场测试案例的执行距离估计误差绝对值在50 m以内,表明了本方法具备有效性,显著提升了现场测试案例执行距离估算精度,为后续合理高效串接现场测试序列提供了有力的依据。

