SMAP 卫星的RBF 神经网络海表盐度遥感反演
赵文杰,李洪平*,刘海行
(1.中国海洋大学信息科学与工程学部,山东 青岛 266100;2.自然资源部第一海洋研究所,山东 青岛 266061)
海表盐度(Sea Surface Salinity,SSS)是研究大洋环流和海洋对气候影响的重要参量,是决定海水基本性质的重要因素之一[1]。目前获取SSS 的方法有现场观测和卫星遥感测量。现场观测是最早用于获取SSS 的方法,但由于其所覆盖海域有限并且时间上无法同步,致使其远远不能描述盐度在不同时间、空间尺度的变化[2]。卫星遥感测量则解决了现场观测的这些不足之处,已成为目前获取SSS 的有效手段。国际上测量盐度与湿度的卫 星主要有SMOS(Soil Moisture and Ocean Salinity)卫星、Aquarius/SAC-D 卫星和SMAP(Soil Moisture Active Passive)卫星,主要探测载荷均为L 波段[3]。Tang等[4]表明,SMAP 卫星可以提供全球SSS 数据,能填补SMOS 和Aquarius/SAC-D 对部分海域SSS 观测的空白。SMAP 卫星于2015 年发射,它的L 波段辐射计用于测量SSS,可以提供大约40 km 以及平滑至约70 km 的较高空间分辨率的SSS 数据。
L 波段(1.400~1.427 GHz)是受国际条约保护并用于无线电天文学研究的波段[5]。L 波段辐射计测量的海面亮温数据与海面粗糙度、辐射计观测角、极化状态、风速和白冠覆盖率等参量密切相关[6]。吴芳芳等[7]研究表明,基于机器学习的方法能有效分析出数据内部的关联性,提高SSS 遥感反演的预测精度。2011 年高国栋等[8]比较研究了径向基(Radial Basis Function,RBF)神经网络和BP(Back Propagation)神经网络在海水盐度建模中的应用,提出RBF 神经网络在海水盐度建模等复杂系统方面具有实用性和可靠性,并具有很好的应用前景。2016 年Zhao等[9]针对南海SMOS 卫星数据,基于主成分回归(Principal Component Regression,PCR)模型反演SSS,最终证明PCR 模型对SSS 反演有效。2017 年邓广和李洪平[10]通过建立亮温拟合回归模型反演南海海域的盐度,有效减小了SMOS 在南海特定时间反演盐度的误差。2018 年李长军等[1]采用BP 神经网络建立基于SMOS 卫星的SSS 反演模型,提高了南海海域SSS 反演精度。2020 年王艺晴等[11]采用RBF 神经网络反演了SMAP 卫星升轨和降轨的SSS 数据,测试结果均较好,残差基本上集中在0.6 以内。2021 年王颖超等[12]采用BP 神经网络的方法,针对SMOS 卫星Level 1 C 级亮度温度数据和辅助数据建立了一种SSS 预测模型,结果表明,利用新模型预测的SSS 比SMOS 卫星的3 个粗糙度模型盐度产品精度高。
RBF 神经网络是以函数逼近理论为基础而构造的一类前向网络,训练速度快,具有很强的非线性映射能力。因此,为了更好地描述SSS 在不同时间、空间尺度的变化,得到更高精度的SSS 数据,本文选取SMAP 卫星的L2C 数据、Argo(Array for Real-time Geostrophic Oceanography)数据和其他辅助数据,利用RBF神经网络修正平静海面亮温,最终基于Meissner-Wentz 介电常数模型进行盐度反演,并对反演结果进行了验证和评估。
1 数据
选取太平洋部分海域(160°E~120°W,0°~30°N)为研究区域(图1)。该海域远离陆地,基本不受陆地射频干扰的影响,是研究海面粗糙度和泡沫覆盖等来自海面的影响因素对SSS 遥感反演影响的最佳区域。
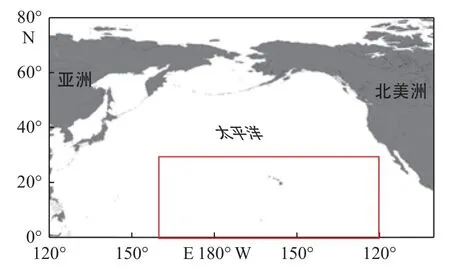
图1 研究区域Fig.1 Study area
1.1 SMAP 卫星数据
SMAP(Soil Moisture Active Passive)卫星是可以同时监测全球土壤湿度和海表盐度的在轨卫星,搭载的是L 波段微波辐射计,采用多极化的极化方式,非天底入射角为40°,重访周期是8 d[6,13],其空间分辨率为40 km,并且被插值到0.25°×0.25°的网格。数据来自Remote Sensing System[13],本文使用2016 年1 月至12 月的SMAP 卫星L2C 数据的SSS_SMAP_40 km 这一卫星盐度反演产品,该产品是在卫星原始40 km 空间分辨率下经过误差修正的盐度数据,用的7 个参量为地球入射角(Earth Incidence Angle,EIA)、海表温度(Sea Surface Temperature,SST)、海面风速(Wind Speed,WS)、海面风向(Wind Direction,WR)、降雨率(Rainfall Rate,RR)、粗糙海面亮温(Brightness Temperature,TB)、SMAP 海表盐度(Sea Surface Salinity,SSS)。
1.2 Argo 数据
Argo 计划是全球海洋观测系统的一部分,旨在快速、准确、大范围地收集全球海洋上层的海水温度、盐度剖面资料。Boutin等[14]指出集中于水深0.5~10 m 的Argo 盐度数据能够作为SSS 数据。本文使用的Argo 浮标实测数据来自Coriolis Data Center[14],采用2016 年1 月至12 月15 070 个站位点有效Argo 浮标的盐度数据作为原始数据,经过时空匹配、天平均等一系列复杂前期处理工作后,将其作为实测海表盐度数据,即Argo 实测盐度数据(Argo SSS)。
1.3 辅助数据
本文的辅助数据包括Global Ocean Waves Reanalysis Waverys 数据[15]和CERA-SAT 数据[16]。Global Ocean Waves Reanalysis Waverys 数据来自哥白尼海洋环境监测服务中心(Copernicus Marine Environment Monitoring Service,CMEMS)[15],采用Météo-France 全球波浪模型(Météo-France global wave model,MFWAM),每日产品的时间分辨率为3 h,空间分辨率为0.2°×0.2°,Law-Chune等[15]指出该数据是目前可供用户用于描述过去海洋状态的最佳数据之一。CERA-SAT 数据来自欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)[16],利用CERA 同化系统创建,Laloyaux等[16]指出该系统利用各种海洋和大气观测资料,并利用耦合模式进行海洋-大气分析,每日产品时间分辨率为3 h,空间分辨率为65 km。本文使用2016 年1 月至12 月的Global Ocean Waves Reanalysis Waverys 中的部分波浪数据和CERA-SAT 中 的TCWV[17]数据作为辅助数据,如表1 所示。
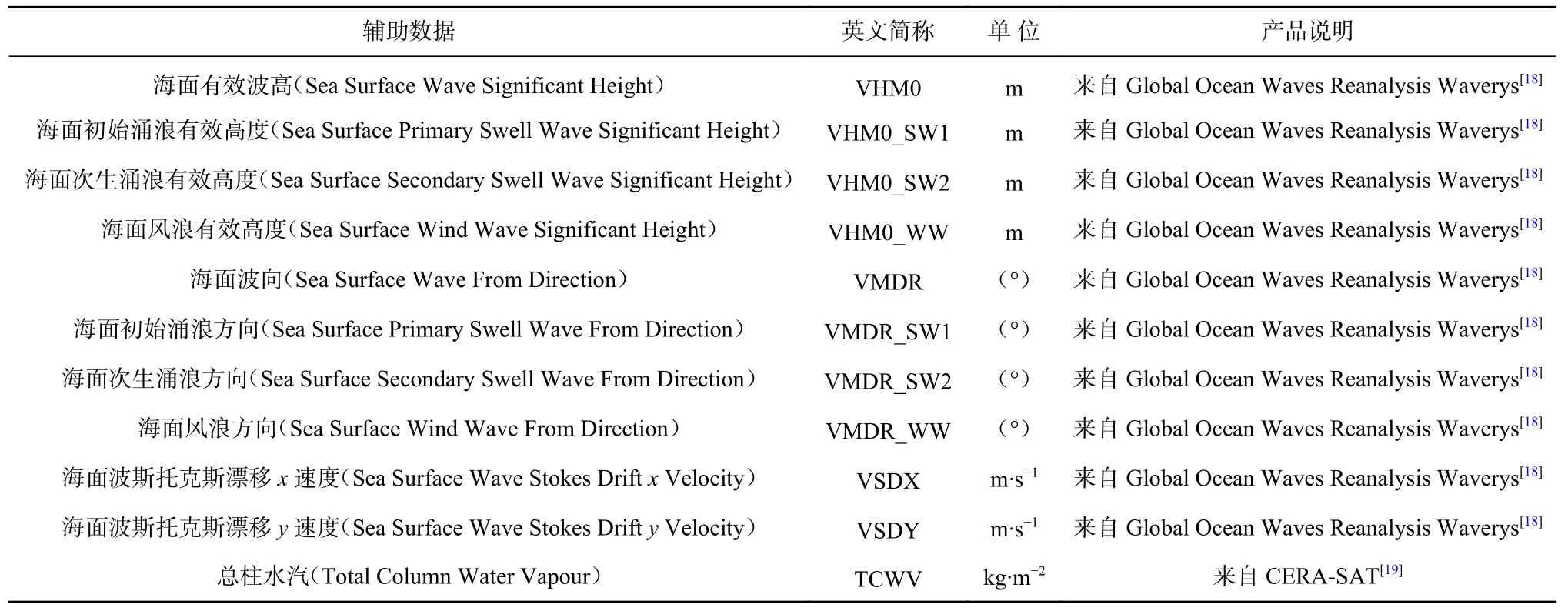
表1 辅助数据产品描述Table 1 Auxiliary data product description
1.4 数据匹配
SMAP 卫星L2C 数据、Argo 数据和辅助数据的时间分辨率和空间分辨率并不完全相同,且本文是以Argo 浮标的盐度数据作为实测SSS 数据,所以在建立模型前首先需要以Argo 数据的时空为基准对3 种数据进行时空上的匹配,得到可用的匹配数据集。在时间上,由于SMAP 卫星数据的重访周期是8 d、辅助数据的时间分辨率为3 h,所以选取与Argo 数据为同一天的SMAP 卫星数据以及时间上相较Argo 数据最近的辅助数据匹配。在空间上,按照SMAP 网格点匹配的方法匹配3 种数据。这种匹配方法可使3 种数据在时空上更为接近,具有更高的准确性和可信度。最终得到匹配数据集共7 395 组有效数据。
2 方法
2.1 数据处理方法
2.1.1 修正SMAP 卫星海面亮温增量计算
Meissner 和Wentz[20-21]提出Meissner-Wentz 介电常数模型(简称M-W 模型),使用双德拜(Debye)方程拟合海水复介电常数。该模型计算平静海面亮温的公式为:
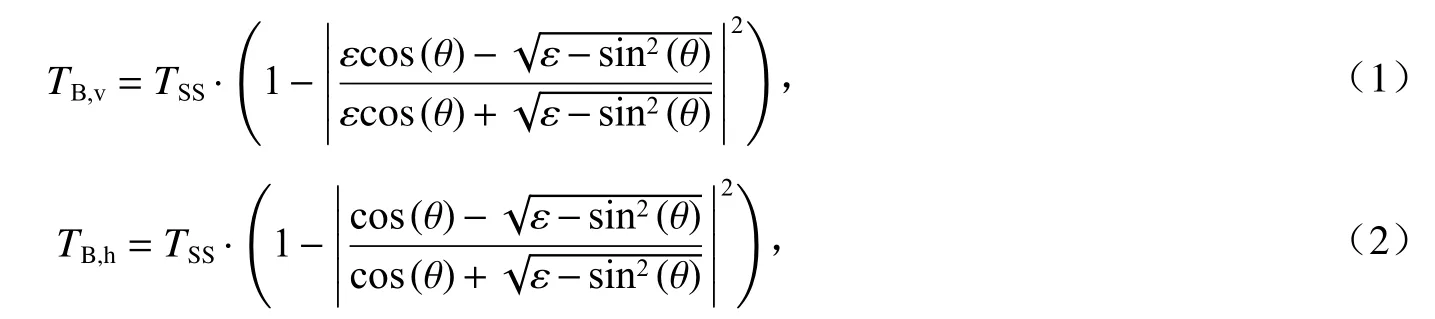
式中:TSS为海表温度;θ为入射角;TB,h为水平极化亮温;TB,v为垂直极化亮温;ε为海水复相对电容率。
利用Meissner-Wentz 介电常数模型对Argo SSS 进行处理,得到实测平静海面亮温TB,flat,p,然后利用ΔTB,p=TB,p-TB,flat,p得到修正SMAP 卫星海面亮温增量ΔTB,p。
2.1.2 泡沫覆盖率计算
一般情况下,海面是不存在白冠覆盖的。当海面不存在白冠覆盖时,微波辐射计所接收到的亮温包括平静海面亮温和由海面粗糙度所致的亮温增益。但是,当风速超过某个临界值时,海面会产生白冠,导致海面亮温进一步增加,此时海面亮温TB,p表示为[6]:

式中:p 为极化方式,包括水平极化h 和垂直极化v;TB,flat,p是平静海面亮温;TB,rough,p是粗糙海面亮温;F是海面白冠覆盖率;TB,foam,p是白冠覆盖海面亮温。
海表白冠对亮温的影响取决于白冠覆盖率及泡沫发射率参数[6],由于泡沫层复杂的微观结构,目前还没有一个普遍通用的亮温或辐射率模式能够很好地描述泡沫层微波辐射率与海面各特征参量间的相互关系[22],因而泡沫发射率参数仍是SSS 遥感测量与研究的难点之一。但是对白冠覆盖率的研究已取得一定进展,Hwang[23]提出了白冠覆盖率模型,利用该模型能够计算海面的白冠覆盖率Wc,公式为:
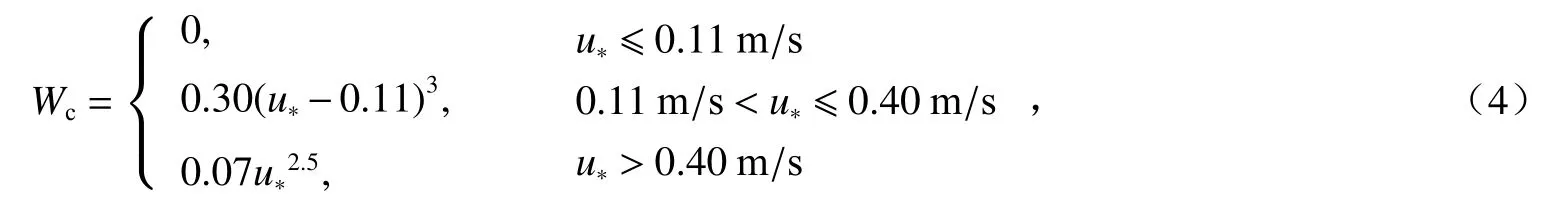
式中:u∗为摩擦速度,其与阻力系数C10、海面风速U10有关,即。当U10≤35 m/s 时,C10=10−4×(-0.016 0U10+0.967U10+8.058);当U10>35 m/s 时,C10=2.23×10−3×(U10/35)−1。
2.1.3 参数筛选
机器学习作为“黑箱”建模,需要科学地选取训练参数。本文使用主成分分析(Principal Component Analysis,PCA)与互信息(Mutual Information,MI)组合的方法进行参数筛选。PCA 是一种降维的多元统计分析方法,常用于确定特征变量的维数;而MI 能在保留强相关特征的同时在一定程度上去除冗余[24]。所以,该参数筛选方法能够解决单一模型的局限性,减少特征变量之间由强耦合性引起的误差。
通常在进行主成分分析时,累计方差贡献率阈值设为85%~95%。首先利用PCA 计算主成分因子的累计方差贡献率,把方差贡献率累加值超过90%作为提取主成分的原则,确定主成分为11 个,然后计算各主成分载荷,将主成分载荷绝对值超过0.4 对应的参量确定为PCA 选取的参量。再分别计算各参量与修正SMAP 卫星海面亮温增量之间的互信息值,得出亮温增量与各个参量之间的依赖程度(表2),选取互信息值较大的参量作为MI 确定的参量。最终利用PCA+MI 方法确定的参量为地球入射角(EIA)、海表温度(SST)、海面风速(WS)、海面风向(WR)、粗糙海面亮温数据(TB)、海面有效波高(VHM0)、海面初始涌浪有效高度(VHM0_SW1)、平均波向(VMDR)、海面初始涌浪方向(VMDR_SW1)、总柱水汽(TCWV)、白冠覆盖率(Wc)。
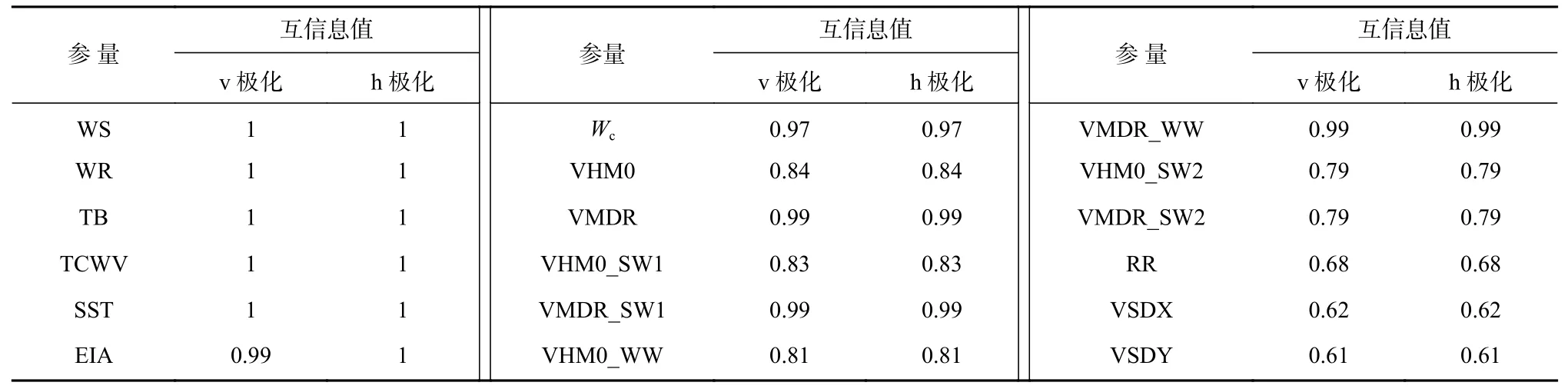
表2 各个参量与v 和h 极化亮温增量间的互信息值Table 2 Mutual information values between various parameters and v/h polarization brightness temperature increment
2.2 基于RBF 的亮温增量模型的建立方法
径向基(RBF)神经网络[25-26]是一种在逼近能力、分类能力和学习速度等方面具有一定优势的神经网络,具有很强的非线性映射能力。它是由输入层、隐藏层和输出层构成的3 层神经网络(图2)。
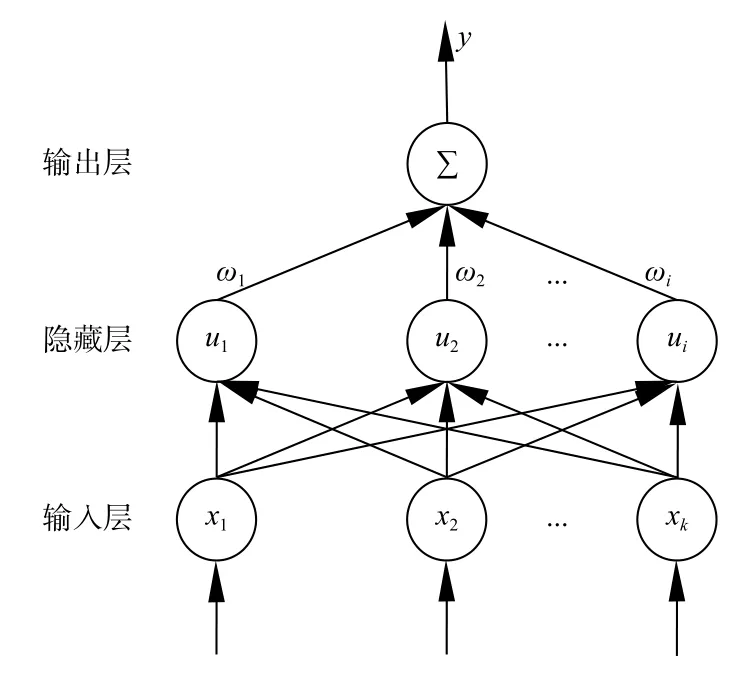
图2 径向基神经网络结构Fig.2 The structure of radial basis neural network
1)第一层是输入层。输入数据并将数据信息传递给隐藏层,对输入信息不进行任何处理。
2)第二层为隐藏层。需要在该层确定其节点数目;隐藏层的核函数也就是径向基函数(一般是高斯函数)[27],公式为:
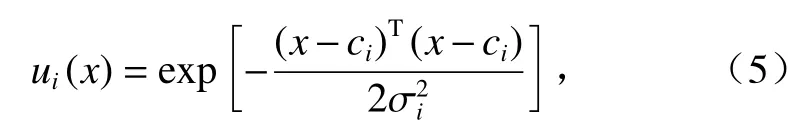
式中:x为样本对象的输入向量;ui(x)为第i个隐层节点的输出向量;σi为第i个隐节点的标准化常数;ci为第i个隐节点的中心向量,与x有着相同的维数。本文采用监督学习算法来确定网络中心和其他权重参数。
3)第三层为输出层。通过该层能得到建立的模型和模型预测的结果数据。
RBF 亮温增量模型是将训练数据集作为输入层,采用高斯函数为激励函数并作为隐藏层,修正SMAP卫星海面亮温增量作为输出层的RBF 神经网络模型。该模型采用监督学习的方法选取径向基函数的中心值和方差。经过训练可以得到RBF 亮温增量模型和训练数据集在训练后的海面亮温增量ΔTB,p。
2.3 反演盐度的计算
时空匹配后的数据按8∶2 的比例随机划分为5 916 组训练数据集和1 479 组验证数据集,以参数筛选后的参量为输入层,海面亮温增量ΔTB,p为输出层,然后利用TB,flat,p=TB,p-ΔTB,p得到模型预测的平静海面亮温TB,flat,p,反演盐度的实验流程见图3。
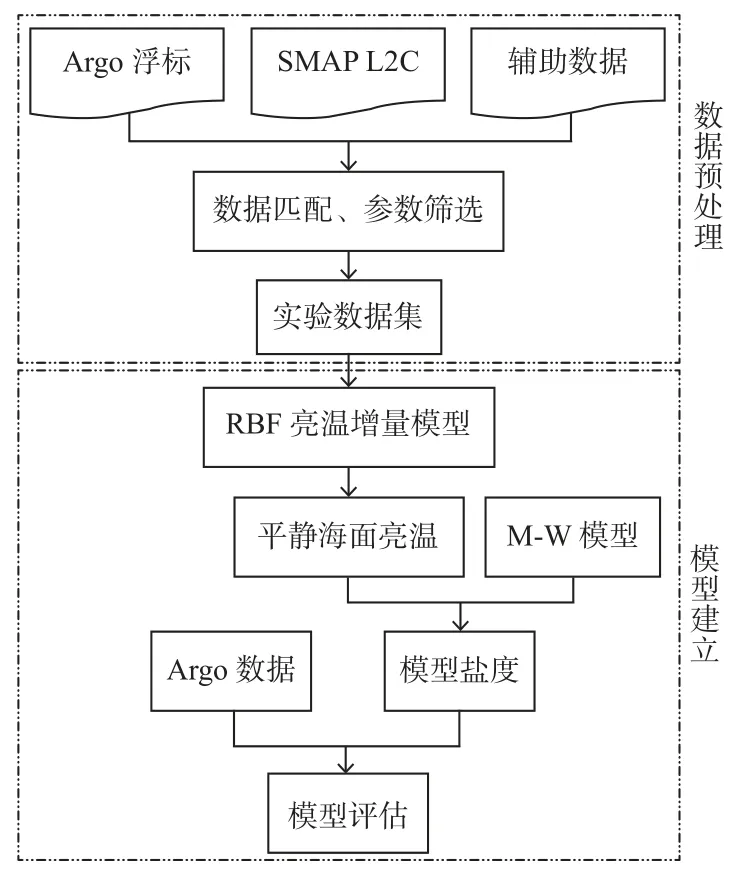
图3 海表盐度反演流程Fig.3 Flow chart of sea surface salinity inversion
根据Meissner-Wentz 介电常数模型[20-21]可知,亮温TB,p最终可以表示为频率(f)、入射角(θ)、极化方式(p,包括h 和v 极化)、海表温度(TSS)和海表盐度(SSS)的函数,即:TB,p=F(θ,f,TSS,SSS)。若其他参量已知,则可以由亮温反演出海表温度,即:SSS=F−1(θ,f,TSS,TB,p)。可知,在已知入射角、频率、海表温度和盐度的情况下,必定会有唯一一对(h 和v 极化)亮温数据。所以,当平静海面亮温的模型预测值越接近实测值时,利用Meissner-Wentz 介电常数模型反演得到的盐度值越接近真实值。
根据Argo 实测的盐度数据可知,研究区域内的全年海表盐度主要集中在32.00~36.00,所以利用Meissner-Wentz 介电常数模型可以计算出该盐度范围内的所有亮温数据,进而得到每一组数据对应的盐度,方法为:首先,利用训练数据集和验证数据集中的每一组数据的入射角、频率(1.41 GHz)、海表温度数据,根据Meissner-Wentz 介电常数模型,计算该组数据在入射角、频率和海表温度数据一定的情况下,盐度范围为32.00~36.00 内对应的所有4 000 对平静海面亮温数据;然后,在求得的平静海面亮温数据中找到最接近模型预测的数据,此时对应的盐度作为最终模型反演的盐度值。
3 结果
利用5 916 组训练数据集进行模型训练过程中,经过反复试验,确定RBF 亮温增量模型的学习率为0.002,学习步数为50 000,隐藏节点数目为20。利用1 479 组验证数据对模型进行验证评估时,由于在数据匹配空间上按照SMAP 网格点进行匹配,所以绘图时每一个点状数值对应的是相应SMAP 格网的盐度值。在SMAP 卫星盐度产品制作流程中,采用风致发射率模型[13]去除海面粗糙度的影响,而本文依据建立RBF的亮温增量模型去除海面粗糙度的影响。基于RBF 较强的非线性映射能力,模型训练之后得到的平静海面亮温值更接近于实际值。但是,除了海面风、海面波浪和白冠覆盖率影响海面粗糙度之外,泡沫发射率参数也会对其产生影响,所以模型训练后的盐度值与实测值还会存在一定差异。
为了评价模型预测盐度和SMAP 卫星盐度产品的数据质量,本文以Argo 实测盐度数据为参考,分别统计分析预测数据和SSS_SMAP_40 km 的绝对误差分布,结果如图4 所示。模型预测盐度和SSS_SMAP_40 km 的绝对误差分别有1 261 组和1 002 组数据集中于−0.5~0.5,分别占验证数据集的85.3%和67.8%。相较SMAP 卫星盐度产品,预测盐度的绝对误差集中分布于−0.5~0.5 的数据更多。此外,SMAP卫星盐度产品的绝对误差超出−1~1 的数据占验证数据集的5.8%,而预测盐度的绝对误差超出−1~1的数据仅占验证数据集的0.7%。由此可知,本文所使用模型预测的盐度数据质量要优于SMAP 卫星的SSS_SMAP_40 km 产品。
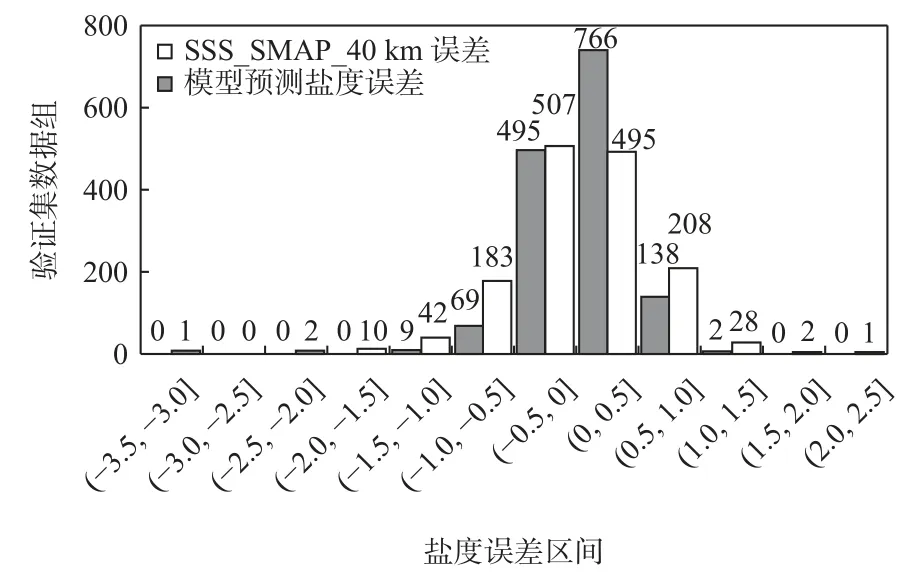
图4 模型预测盐度和SSS_SMAP_40 km 的绝对误差Fig.4 Absolute error diagram of model prediction salinity and SSS_SMAP_40 km
本文是在未考虑位置因素的前提下按照8∶2 的比例随机划分的数据集,所以随机性较大,导致本次验证数据集中只有1 月的数据位于(160°E~120°W,0°~30°N)范围内,其余月份数据均位于(160°E~180°,0°~30°N)范围内。为了对比同一经纬度范围内模型预测盐度与Argo 实测盐度以及SMAP 卫星盐度,本文选取部分太平洋海域(160°E~180°,0°~30°N)内的Argo 实测盐度数据、模型预测盐度数据和SSS_SMAP_40 km 数据,分析这3 种盐度的空间分布特征。由Argo 实测盐度空间分布(图5)可以发现,在该区域内盐度北高南低,尤其在20°~30°N 区域内盐度相对较高。对比模型预测盐度的空间分布(图6)和Argo 实测盐度空间分布(图5)发现:该区域内盐度大致也呈北高南低分布;在20°~30°N 区域模型预测盐度值普遍低于Argo 实测盐度值,但其整体误差在精度允许的范围内;模型预测的结果较为稳定,全年并未出现异常高或异常低的盐度值现象。对比SMAP 卫星盐度的空间分布(图7)和Argo 实测盐度空间分布(图5)发现,该区域内盐度也大致呈北高南低分布,但在20°~30°N 区域内SMAP 卫星盐度普遍高于Argo 实测盐度值,且存在误差较大的区域,如2 月在(180°,20°N)附近、8 月在(170°E,20°N)附近的盐度值均在36.2 左右,Argo实测盐度值均在35.2 左右,误差均接近于1。在0°~20°N 区域内SMAP 卫星盐度还存在明显低于Argo 实测盐度的情况,SMAP 卫星盐度产品的稳定性相对于模型预测盐度较差。就整体而言,SMAP 卫星盐度产品在该区域内全年盐度还呈现出略高于Argo 实测盐度的趋势。从这3 种盐度空间分布的对比分析可以发现,相较于SMAP 卫星盐度产品,模型预测盐度不仅精度更高,而且其整体的稳定性也优于SMAP 卫星盐度产品。
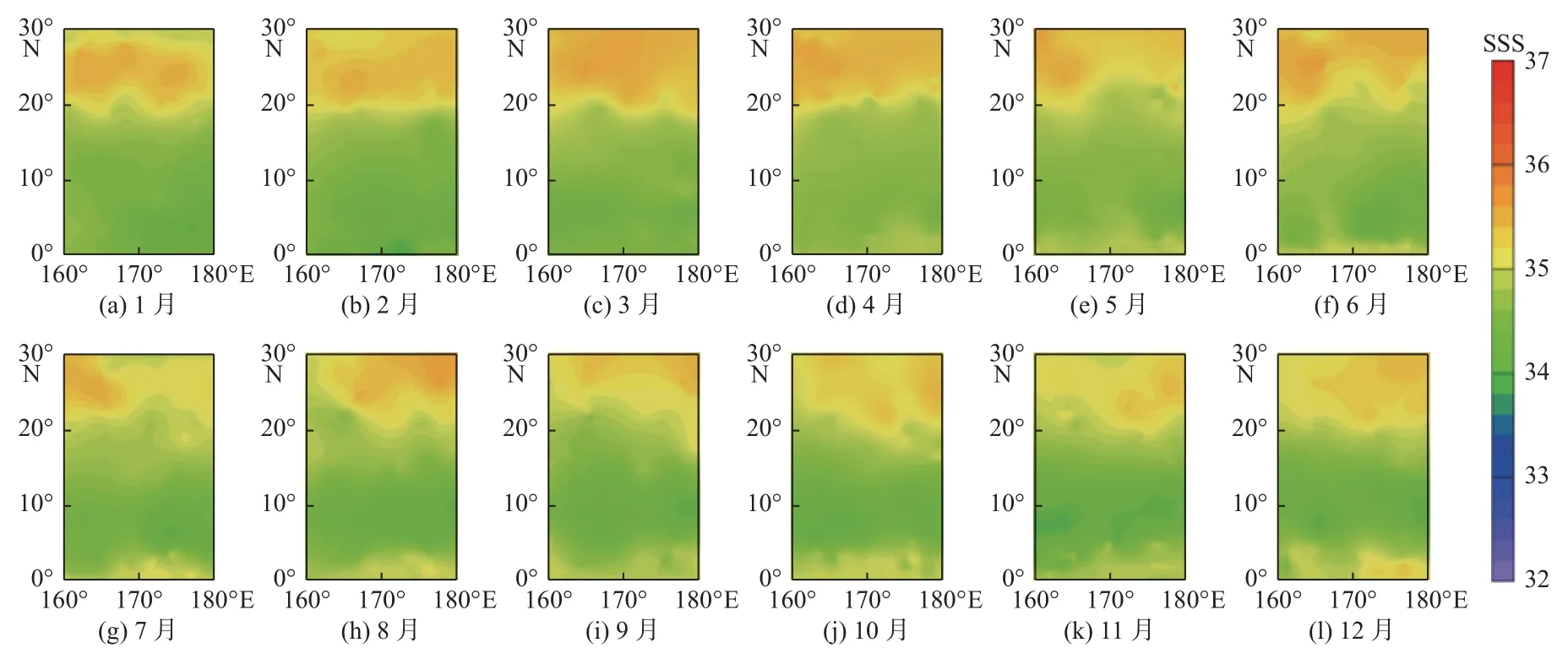
图5 Argo 实测盐度空间分布Fig.5 Spatial distribution of Argo salinity
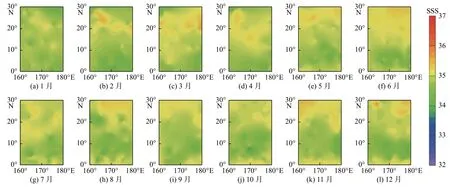
图6 模型预测盐度空间分布Fig.6 Spatial distribution of model prediction salinity
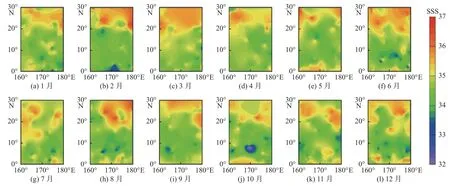
图7 SSS_SMAP_40 km 空间分布Fig.7 Spatial distribution of SSS_SMAP_40 km
为了定量评价模型预测盐度和SMAP 卫星盐度的精度及稳定性,本文采用了均方根误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)、最大绝对误差和最小绝对误差四种精度评价指标分析模型预测盐度和SSS_SMAP_40 km。统计模型预测盐度和SSS_SMAP_40 km 的误差(表3)可知,相较于SMAP 卫星盐度的RMSE(0.5)和MAE(0.4),模型预测盐度的RMSE(0.4)和MAE(0.3)更接近于0,说明模型预测盐度的精度更高;相较于SMAP 卫星的最大绝对误差(2.2)和最小绝对误差(−3.2),模型预测盐度的最大绝对误差(1.0)和最小绝对误差(−1.3)更接近于0,表明模型预测盐度的稳定性更好。综上可知,与SMAP 卫星盐度产品相比,本文建立的模型具有更高的精度和更好的稳定性。

表3 模型预测盐度和SMAP 卫星盐度产品相对Argo 盐度的误差Table 3 Errors of model prediction salinity and SMAP salinity products relative to Argo salinity
对比分析模型预测盐度、Argo 实测盐度以及SMAP 卫星盐度结果表明,本文采用PCA+MI 的参数筛选方法确定的海面风、海面温度、海面波浪、总柱水汽和白冠覆盖率等参量建立亮温增量模型具有可行性,最终基于RBF 神经网络建立的模型相对于SMAP 卫星算法也能提高盐度数据的精度。
4 结语
海表盐度的分布与变化在海洋环流、水循环和碳循环等大尺度过程中起到非常重要的作用[22]。为提高海表盐度遥感反演的精度,本文建立了RBF 亮温增量模型来进行SMAP 卫星的海表盐度遥感反演。对比分析模型预测盐度和SSS_SMAP_40 km 相对于Argo 实测盐度的误差发现,模型预测盐度的各项误差均低于SMAP 卫星盐度误差,且模型预测盐度误差更集中于−0.5~0.5,本文建立的模型能够生成质量明显优于SMAP 卫星产品的盐度数据,其盐度空间分布也更接近于Argo 实测盐度的空间分布,实验结果充分证明了本文方法的可行性。
本文在进行盐度遥感反演时,仅仅将海面风、海面温度、海面波浪、总柱水汽和白冠覆盖率等影响因素纳入反演模型中,但除了这些因素外,还存在泡沫反射率参数[23]等其他影响因素,输入模型的参量还需进一步补充,并且本文的训练样本有限,仅仅以部分太平洋海域为研究对象,所以,本文模型还需进一步完善。未来,在研究中将结合更多SSS 反演影响因素不断优化模型,同时选取不同的海域作为研究对象,在提高盐度遥感反演精度的同时将模型应用于全球海域。

