环形张拉式索网可展开天线创新设计与分析

唐雅琼，李团结，陈聪聪

(西安电子科技大学 机电工程学院，陕西 西安 710071)

空间大型可展开结构是未来建造天基(Very Long Baseline Interferometry，VLBI)、全球降雨雷达系统、空间太阳能电站、大型空间军事基础设施的关键部分。为了满足火箭运载体积和重量的限制，索网结构已经成为实现空间可展开天线大型化、轻重量与高收纳比的最佳结构方案之一[1-4]，已经涌现出许多在轨应用的案例，例如亚洲蜂窝卫星ACeS携带17 m的 L频段伞状可展开天线；日本HALCA卫星携带8 m的 Ku频段径向伸展式可展开天线；日本工程实验卫星ETS-VIII携带两部19 m×17 m 的S频段构架式可展开天线；我国环境一号C星携带的6 m×2.8 m的S频段构架式可展开天线；美国商业通信卫星TerreStar-1携带18 m的L频段Y形折叠肋可展开天线；美国移动宽带通信卫星SkyTerra-1携带22 m的环向Y形肋可展开天线；美国Thuraya系列通讯卫星、美国气象卫星、日本MBSat移动广播卫星、欧洲第四代国际通信卫星Inmarsat-4 F1以及我国天通一号卫星携带的12 m～20 m环形桁架可展开天线等。

索网天线由索网结构、支撑桁架、金属丝网和馈源组成。索网在桁架和预紧力作用下张成一定的形状，用于铺附金属丝网反射电磁波。按照桁架为索网提供的边界类型，索网天线可分为闭环支撑(如环形桁架可展开天线)和开环支撑(如伞状可展开天线)两种结构形式[5]。相比于开环支撑，闭环支撑可为索网结构提供较为完备的边界条件，具有更轻的质量、更小的装载体积以及更小的表面反枕误差，因此在大型可展开天线中占有非常重要的地位和发展潜力[6]。在索网天线设计中，索网找形是决定天线能否实现预定功能的重要环节。索网找形分为以形找力、以力找形和力形耦合3种，它的目标是设计出具有足够高形面精度和刚度的索网几何和预张力。所采用的数学建模方法包括解析法、动力松弛法、力密度法和非线性有限元法等[7-20]。TIBERT等[11-12]提出一种基于力密度的索网天线预张力设计方法。这种方法首先通过力密度方法找到网面的平面极小长度构型，得到索网节点在平面上的坐标值，然后将平面的构型垂直投影到抛物面而得到竖向坐标，根据投影后索网节点位置建立力平衡方程度并计算得到竖向索张力。该方法基于特征值分析和光谱分析方法，建立不满秩节点平衡矩阵的迭代格式，以计算力密度的可行解。MORTEROLLE等[13]提出了一种考虑几何约束的改进力密度法。这种找形方法以力密度作为迭代参数，根据每一根索段的张力与给定张力的差值修正当前的力密度值，通过循环迭代使得索段张力和节点位置满足给定的张力要求，继而逐步扩大到索段周边的索段，最后扩展到整个索网反射面，整体实现索网张力的均匀分布。TANAKA等[14-15]利用由力密度求解出的索段力与由胡克定律求得的索段力满足一致性的条件，来进行索网反射面的预张力设计，并首次提出了考虑桁架变形的找形设计算法。LI等[16]提出了考虑桁架变形的两步法：第1步将索网边界固定对索网张力进行设计；第2步，优化与桁架相连的索段预张力来减少支撑结构变形对索网张力的影响。两步法揭示了索网与桁架耦合变形机制，方法简单有效，形成了考虑桁架变形找形设计方法的基本轮廓。NIE等[17-18]研究了索、梁和铰链组合结构的预张力设计方法，并以典型轨道位置的天线形面误差为指标，综合考虑了热变形与弹性变形的影响。针对热环形、加工制造等不确定性问题，DENG等[19-20]提出了区间力密度找形设计方法。

索网找形发展至今，已从最初的纯索网找形，发展为考虑桁架变形、空间热环形、加工制造不确定性等面向工程实际的索网找形。但是，对于现有的索网天线类型，索网往往被包裹在桁架的内部，在索网张紧时桁架变形是不可避免的，即使不少学者提出了考虑桁架变形的索网天线找形设计方法，尝试通过对桁架结构进行变形补偿来提高形面精度，依然不能达到特别好的效果。随着结构尺寸的增大，空间可展开天线越来越多地采用细长杆作为支撑结构。细长杆具有大的抗拉压刚度和较小的抗弯曲刚度，考虑桁架变形的找形设计方法，虽然可以在某种程度上减小桁架变形对形面精度的影响，但并不能避免桁架受到弯矩的影响。为此，笔者提出一种环形张拉式索网可展开天线，实现了杆只受压而不受弯，大大降低了支撑结构的弹性变形，提高了索网可展开天线的设计精度。

1 构型设计

环形张拉式索网可展开天线反射面如图1所示，由支撑结构和索网结构两部分组成。支撑结构包括压杆、加强索和拉索，压杆和拉索承受轴向压力，加强索用于提高结构整体刚度。索网结构由前索网、张紧索和背索网组成，前索网在张紧索和背索网的共同作用下张成反射面的形状，用于支撑金属网反射电磁波。索网结构通过外围节点与支撑结构相连。在发射阶段，压杆折叠、整体沿径向收缩以减少体积，发射到预定轨道之后结构展开，并具备反射电磁波的功能。

2 分块式节点力平衡方程

在单元预紧力的作用下，索网天线节点自平衡方程可以写成如下形式，

MF=0，

(1)

其中，M∈RNn×Nm为自平衡系数矩阵；R为矩阵维数；Nn为节点数；Nm为单元数，0表示零矩阵。如果节点i和节点j相连构成单元m，则M第3i-2行、第3i-1行和第3i行取值为

(2)

(3)

(4)

其中，(xi，yi，zi)和(xj，yj，zj)分别表示节点i和节点j的坐标；lm表示单元计算长度，当单元为拉索时，计算长度为单元长度的正值，当单元为压杆时，计算长度为单元长度的负值，即

(5)

通过引入计算长度，可以将式中压杆单元和拉索单元预紧力的符号统一为正值，便于优化求解。为了降低方程求解的复杂度，需要进一步将单元和节点进行分类。根据单元和节点所处位置，将单元分为支撑单元和索网单元；将节点分为索网节点、支撑节点和共用节点。

根据不同的单元类型，为单元编号定义如下3个集合，

{m|m∈Sm，m为单元编号} ，

(6)

(7)

(8)

上述单元编号集合满足如下关系：

(9)

同理，根据不同的节点类型，定义集合如下，

{n|n∈Sn，n为节点编号} ，

(10)

(11)

(12)

(13)

上述节点编号集合满足如下关系关系：

(14)

根据上述的分类方式，索网天线节点在单元预紧力下自平衡方程式可整理成如下分块形式：

(15)

找形设计实际上就是对方程进行优化求解，为了降低求解难度，将式展开成如下两种递推方程的形式：

递推方程1MccFc=0，

(16)

(17)

递推方程2MobFb=0，

(18)

(19)

上述两种递推方程实际上反映了两种找形设计方法。第1种，先对索网结构找形，再将索网的预紧力作为外力施加到支撑框架上，再对支撑结构找形；第2种，先对支撑结构找形，再将支撑结构的预紧力作为外力施加到索网结构上，再对索网结构找形。两种方法所用到的优化求解算法是一致的，因此下面仅介绍基于第一类递推方程的找形设计方法。

3 找形设计方法

索网反射面找形设计的目的是使反射面具有高形面精度的同时，还具有抵抗外界干扰的能力，即在保证索网具有一定几何状态的前提下，寻找一组较均匀的预张力，使整个结构自应力平衡。

3.1 索网结构找形

当结构形状给定时，方程是典型的齐次线性方程组。当Mcc核空间维数dimN(Mcc)大于1时，存在无穷多组预张力可使索网结构在当前几何状态下达到力平衡。这些预张力的值可以表示为

(20)

对于索网结构，我们希望找到一组均匀、大于零的预紧力，使得结构更加稳定。为此，建立如下的优化模型，

(21)

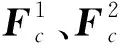
上述求解方法可以称为“以形找力”，即在给定结构形状的情况下，寻找一组平衡预紧力。但是当Mcc核空间维数dimN(Mcc)小于等于1或者找不到满足所有约束条件的解时，说明当前几何状态无法实现力平衡。这种情况下，需要对索网结构进行“力形耦合设计”。

力形耦合设计通常基于力密度方程进行。力密度方程将节点几何信息和力信息通过引入力密度实现解耦，使得优化求解更加容易。

将式写成力密度的形式：

(22)

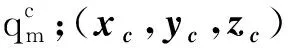
在求解式的过程中，当给定单元的力密度值时，获得新的节点坐标。为了获得具有一定形面精度的几何-预张力状态，建立如下优化模型：

(23)

通过优化求解式(21)或者式(23)，可以获得一组较为理想的索网结构几何和预紧力(xc，yc，zc)和Fc，进而计算出等式的右侧，即可对支撑结构进行找形。

3.2 支撑结构找形

(24)

同样，笔者希望找到一组均匀、大于零的预紧力使得结构更加稳定，为此建立如下优化模型：

(25)

当方程系数矩阵的秩与其增广矩阵的秩不相同时或者上述优化模型找不到满足所有约束条件的解时，需要开展力形耦合设计。将式写成力密度方程形式：

(26)

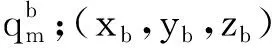
为了获得具有一定形面精度的几何-预张力状态，建立如下优化模型：

(27)

通过求解上述方程，即可实现索网约束条件下的支撑结构力形耦合设计。

4 数值仿真算例

反射面示意图如图2所示。

令反射面口径D为22 m，压杆内圈直径d为20 m，前索网和背网均为焦距16 m的抛物面，反射面整体高度H为4 m，桁架边数B为18，最内圈索网周向分段数为B，次圈为2B，第3圈为3B，第4圈为4B，第5圈为5B，第6圈为6B，最外圈为6B。经分析知，索网结构自平衡方程系数矩阵的核空间维数为653，因此可以采用式对其进行找形设计。找形后的预紧力如图3和图4所示。前索网索段最大预紧力为103.04 N，最小预紧力为10.12 N；张紧索最大预紧力为4.65 N，最小预紧力为0.50 N。因为背索网与前索网对称，所以其预紧力分布与前索网相同。

然后将索网结构的预紧力作为外力加载到支撑结构上对其进行找形。通过分析可知，支撑结构的静平衡系数矩阵的秩与其增广矩阵的秩相同，核空间维数为99，因此直接采用式(25)对其进行找形设计。找形后的预紧力如表1所示，表中正预紧力表示单元受拉，负预紧力代表单元受压。对照图2第3张图可以看出，支撑结构所有杆受压，索受拉。拉索3和压杆8、9、10作为主要承载单元具有较大的预紧力，而加强索1，2，4，5取较小的预紧力。

最后，设索的弹性模量为20 GPa，泊松比为0.3，截面形状为半径为1 mm的圆截面；梁的弹性模量为150 GPa，泊松比为0.3，截面形状是半径为100 mm的圆截面。采用Link 10单元和Link 8单元分别模拟拉索和压杆，建立索网反射面的有限元模型，对找形结果进行验证。考虑结构的弹性变形，不考虑重力的影响，经过静力分析得到的节点位移云图如图5所示。位移为0处施加了边界约束。从图5中可以看出，节点最大位移为 0.090 mm，经计算，前索网均方根误差(形面误差)为0.054 mm，即在考虑结构弹性变形时，结构依然具有很高的形面精度。

>表1 支撑框架预张力分布

5 结束语

通过引入张拉结构思想，以索受拉、杆受压为约束，笔者提出了一种环形张拉式索网可展开天线，并提出了基于分块式节点力平衡方程的“以形找力”和“力形耦合设计”找形方法。最后通过数值仿真分析，得出以下结论：

(1) 所提出的环形张拉式索网可展开天线中，杆单元预紧力为负值，索单元预紧力为正值，表明所有杆受压、索受拉；

(2) 有限元仿真结果表明前索网节点均方根误差为0.054 mm，说明结构在考虑弹性变形时，依然具有很高的形面精度。

笔者提出的环形张拉式结构和找形设计方法，可为今后高精度索网可展开天线设计提供新的思路。