模糊聚类下的接入点选择匹配定位算法

秦宁宁，张臣臣

(1.江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122；2.南京航空航天大学 电磁频谱空间认知动态系统工信部重点实验室，江苏 南京 211106)

全球定位系统(GPS)的广泛使用使室外定位有了一套成熟的解决方案[1]。但由于室内墙壁的阻挡，全球定位系统无法为用户提供高精度的室内定位，使得室内定位技术成为了当前导航定位领域中的一个研究重点。在众多的室内定位方法中，由于室内可探测到多个WiFi接入点(Access Point，AP)，且其信号易于测量，使得基于WiFi接收信号强度(Recevied Signal Strength，RSS)的指纹定位方法成为当下最流行的定位技术之一[2]。该方法通常分为离线和在线两个阶段：离线阶段采集定位区域中参考点(Reference Point，RP)的接收信号强度作为指纹库；在线阶段获取实时定位数据与指纹库进行匹配，获得估计位置[3]。

k近邻查询是最常见的指纹定位算法，但此算法需要待定位置与数据库中的所有数据依次进行对比，计算耗时且需要较大的数据内存作为缓存。因此，为降低对数据库容量的高要求，通常将离线的庞大指纹库进行聚类预处理，待定位的在线数据经分类后，减少匹配量[4]。基于此思想，文献[5]中使用k均值算法对指纹进行聚类，但其定位精度受聚类数量影响较大；文献[6]中提出的AAPC算法提高了WiFi指纹的聚类质量，定位精度相较k均值聚类有所提升，但其忽略了待定位点位于两个聚类边界时的误判风险；文献[7]中提出VAPFC聚类算法，以接入点为离散点生成泰森多边形，多边形区域形成自发的聚类空间，但此算法依赖已知接入点位置，普适性较低。

除了离线的聚类方法会对定位结果造成一定的影响外，接入点信号的可靠性也是影响定位精度的重要因素[8]。由于室内可检测到的接入点数目日渐增多，由噪声或冗余接入点信号带来的干扰影响也随之增大。正如文献[9]中指出的那样，室内环境中并非所有的接入点都有助于定位，某些以通信为目的而安装的接入点信号不仅会增加计算的复杂度，还可能对定位精度带来不利影响。为减少冗余接入点，文献[10]提出基于最大值的接入点选择策略；CHEN等[11]则根据信息熵的理论，提出一种infoGain的接入点选择框架；ZHANG等[12]提出了分区费希尔准则模型，基于费希尔准则对接入点进行选择。上述几种方法虽然都被证明可以以较少的接入点来保证一定的定位精度，但所需的接入点数目却依旧需要人为指定，仍存在接入点过少时误差大，接入点过多时数据库冗余的配置尴尬。

针对上述聚类方法以及接入点选择对定位效率和精度的影响，笔者给出了一种低配移动终端适用的室内定位方法——基于模糊聚类的精简接入点匹配定位算法(Simplified Access point matching location algorithm based on Fuzzy Clustering，SAFC)。该算法仅依赖单一信号源接入点的信号强度，在模糊聚类机制下，将定位区域切分为存在共性交叉的子区域，综合考量信号稳定性与可见性的双效能力，减少每个区域中数据匹配时的工作量，建立区域最小接入点辨识集，最后以速度后验的方式修正定位结果。

1 系统模型

不失一般性，假设定位区域Ω内，可探测到N个接入点信号PA1，PA2，…，PAi，…，PAN；部署M个指纹参考点RP1，RP2，…，RPi，…，RPM。如无特殊说明，文中的相关数据描述如下：

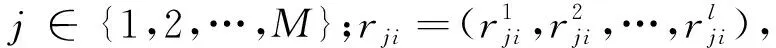
(2)Mj={μj1，μj2，…，μjN}，表示RPj处采集的N个接入点的接收信号强度测量均值集合，μjs表示在RPj处采集的PAs的信号均值。

(3)Sj={σj1，σj2，…，σjN}，表示RPj处采集的N个接入点的接收信号强度测量值Fj的标准差集合，σjs表示在RPj处采集的PAs的信号标准差。

(4)Ω(PAm)表示将参考点划归至以PAm为聚类标签的子区域，简记为Ωm。

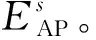
2 离线阶段

2.1 指纹模糊聚类

由于室内环境下相邻参考点的最强接收信号极有可能来自相同的接入点，一种简单的聚类思想便是基于最大信号均值的接入点进行聚类[13]。即对于参考点RPj而言，若其接收到PAi的信号均值最大，即有μji=max(Mj)，则RPj∈Ωi。此方法简单，计算成本低，但并未考虑到均值不同的接入点信号分布可能高度重合的情况。尤其是在复杂的室内环境中，仅通过信号均值最大的接入点对参考点进行聚类，极有可能导致在线阶段多个相似的高接入点信号强度下的分区误判。

基于接入点最大均值聚类通常是以接入点的标号作为参考点聚类的唯一依据，缺乏对信号强度指示信息的考量。但笔者将参考点以最强接入点为分类标签，通过推论高接入点信号间总体均值差异的显著程度，提出一种基于T检验的模糊聚类方法。图1给出两种不同的聚类方法。相比于图1(a)中的最大均值聚类，图1(b)对高接入点信号间总体均值差异不显著的参考点设立模糊类别Ωi&Ωj，最大程度地避免了将相邻参考点聚为单一的Ωi或Ωj，可以有效地克服接入点信号波动造成的聚类结果过于武断的不足。

2.1.1T检验相关描述

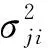
(1)

(2)

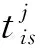
2.1.2 参考点聚类流程

使用T检验方法检验参考点处均值最大的接入点与其他接入点信号总体分布的均值差异是否显著，获取每个参考点的最强接入点集合，进而对整个定位环境进行区域划分，是所提模糊聚类算法的核心思想。

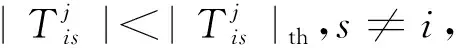
基于T检验判别机制的模糊聚类思想，对RPj进行区域聚类的流程如下：

输入：Mj，Sj，l，α；

输出：Lj。

步骤1 Initialize：Lj=φ；∥φ表示空集

步骤2i=index(max(Mj))；∥index为获取最大值索引的函数

步骤3Lj=Lj∪i； ∥纪录i为RPj处最强接入点的标号

步骤4 Fors∈{1，2，…，N}，s≠i；

步骤8Lj=Lj∪s； ∥增补s进入Lj

步骤9 End If；

步骤10 End For； ∥遍历N个接入点后，获得RPj所属类别标签集合

步骤11 ReturnLj。

若|Lj|>1，则表明RPj处存在多个最强接入点，RPj应判定属于多个区域。遍历Ω中所有参考点，进而完成其区域归属的划分。

2.2 最小接入点辨识集合的获取

离线阶段探测到的某些接入点信号不利于在线定位，有必要在聚类后的每个子区域中对于定位使用的接入点进行选取。为获得辨识度最高的精简接入点集合，给出了两个能够体现信号对定位判别影响的新指标，以解决噪声接入点降低定位精度和冗余接入点增加计算成本的问题。

2.2.1 信号稳定可见性预筛选

接入点信号的稳定可见性主要体现为参考点处的接入点信号在时间上的稳定性与在空间内的可见性。

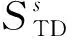
(3)

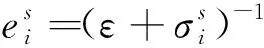
(4)

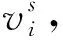
(5)

(6)

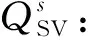
(7)

2.2.2 快速相关性滤波算法去冗余

为获得最小接入点辨识集合，采用快速相关性滤波(Fast Correlation-Based Filter，FCBF)算法对接入点进行过滤。FCBF算法是一种基于无关、弱相关且冗余、弱相关非冗余和强相关4类特征的特征选择框架，其保证输出的结果至少具备后两种特征[16]。若将每个参考点视作为一个类，每个接入点视作为一个特征，则室内定位问题可转化为分类问题，可将FCBF用于提取每个区域中接入点的最小辨识集合。

(1) 子区域内接入点相关性分析

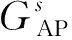
(8)

其中，G(RP|PAi)表示PAi与Ωs内参考点的互信息增益；H(RP)表示当接入点值未知时在Ωs内参考点的信息熵；H(PAi)表示在Ωs内PAi的信息熵。

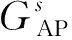
(2) 接入点间冗余性分析

(9)

其中，G(PAi|PAj)表示在Ωs中PAi和PAj的互信息增益。

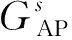
2.3 离线指纹库的建立

模糊聚类和最小接入点辨识集合的筛选过程，帮助每个参考点在离线构建指纹库的过程中，直接面向有效和高辨识价值的精简接入点集合采集数据，在降低数据保存成本的同时，也提高了数据的质量。每个参考点根据所属子区域内的EAP获得精简后的接收信号强度均值向量，连同参考点坐标上传至数据库中存储，形成离线指纹数据库。

3 在线阶段

3.1 基于接入点最大值的区域判定方法

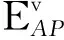
3.2 待定位点位置的预估

在传统指纹定位中，通常使用欧氏距离度量在线数据与离线指纹的相似度。但欧氏距离将接收信号强度向量各个维度之间的差值等同对待，并未考虑不同接入点信号所表示的距离可信程度的差异。考虑到稳定性较差的接入点信号携带的定位信息有限，故可通过对接入点赋权，利用区域内接入点的稳定性对传统欧氏距离度量进行修正。

若判定TP∈Ωv，则基于该区域内接入点的稳定性，TP与Ωv内参考点RPj的信号距离dj被表征为

(10)

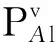
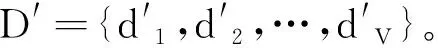
(11)

其中，wk为修正欧氏距离后第k个近邻点权重值。wk的公式如下：

(12)

3.3 基于速度约束的定位结果验证

由于接入点缺失或物理阻挡等因素导致的定位野值点，会严重影响定位系统的性能。当待定位用户在室内移动时，短时段内速度变化不会太大，故可采用基于速度的加权滑动窗作为约束，对可能出现的定位野值进行筛选。

定义加权速度滑动窗Gm，记录用户在前m个时间段的平均速度，通过判断定位前一时刻到当前定位时刻的行进速度是否在Gm速度阈值内，对定位结果进行验证。

不失一般性，假设在tn时刻TP定位坐标为(xn，yn)，则在[tn-h，tn-h+1]时间内，用户的平均速度为

(13)

令Δth=tn-tn-h，定义与当前定位时刻间距成反比的权重配置wh，以提高近定位点时刻用户速度的定位价值：

(14)

得Gm速度

(15)

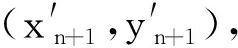
(16)

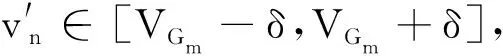
4 定位流程

笔者所提SAFC定位算法的流程如图2所示。离线阶段，SAFC采用模糊聚类机制，以接入点信号的总体均值差异和单次测量的波动程度为参考进行区域划分，并在每个子区域中筛选定位辨识度最佳的接入点信源集合，有效地回避了不稳定接入点造成的区域误判及定位复杂度高的问题；在线阶段，利用修正距离预估位置，结合速度后验筛选定位野值，返回定位坐标或区域，使定位结果的可信度更高。

为保证算法的初始启动，待定位用户初次发出定位请求时，由于无前m个时间段的平均速度，不进行定位检验，直接向用户输出预估坐标；滑动窗Gm构建完成后，算法正式启动。若发现定位野值，则只向待定位用户输出所在区域。此为定位精度与定位可靠性的折中处理，在大型商场等定位场景中可极大地提高用户的定位体验。

5 实验场景与结果分析

5.1 测试场景与数据处理

为验证SAFC定位算法的性能，在江南大学物联网工程学院C区四楼进行数据测试。在60 m×42 m的室内环境中，沿走廊均匀设置368个参考点，相邻参考点间隔1 m，每个参考点处采集50次指纹数据，采样间隔为2.3 s。离线阶段在整个定位区域共探测到105个位置未知的接入点，将其按照Mac地址从1至105编号，每个参考点处未探测到的接入点信号强度值用-100表示。离线阶段的数据采集工作分4天完成，测试点数据在3天后采集，测试人员在走廊中间匀速行走两周共采集到370个测试数据进行后续实验。在数据采集时，测试环境中人员走动频繁，所有数据均在Matlab 2018b中进行处理。

5.2 实验结果与分析

5.2.1 T检验模糊聚类效果

按照节2.1.2中的聚类流程，在2 520 m2的实验场景中，形成11个子区域。因文中所提聚类算法是以接入点的编号作为每个子区域的标签的，故所形成的区域为Ω2、Ω4、Ω6、Ω10、Ω12、Ω14、Ω16、Ω32、Ω33、Ω35及Ω74，如图3所示。由于SAFC考虑了每个参考点处高强度接入点信号总体分布的均值差异，所以会出现同一个参考点被判定属于两个区域的情况。但由于这些参考点的存在，使得处于两区域交界处的待定位点，其接入点信号值无论怎样波动使其被判定属于哪个区域，都不会出现较大的误差。此外，聚类的结果也说明，该聚类方法只有有限几个参考点会被聚类至多个类别，因此增加的工作量是可控的。

在图3中RP1、RP2和RP3处各采集300次接收信号强度进行分析，每个参考点处均值最强的两个接入点信号重叠情况如图4所示。RP1和RP2最强接入点的接收信号强度测量均值差异不明显，依据T检验模糊聚类将这两个参考点同时划分到Ω6和Ω35。在RP3处两个接入点信号的测量值虽有少许重合，但其数据总体均值差异显著，且单次采样时PA6的信号强度均为最大值，故只判定RP3∈Ω6，这也进一步证明了所提聚类算法的合理性。

5.2.2 实验参数选择

为使定位系统的性能达到最佳，对节3.2中的参数Ps和阈值γ进行测试寻优。在K=3时，把每个子区域中P∈{3，4，…，25}与γ∈{0，0.01，0.02，…，0.3}的所有取值组合。在每个子区域的离线数据中随机选择10%作为测试数据，其余为训练数据，重复10次试验取定位误差ρ的平均值。选择每个子区域中最小定位误差的组合作为该区域的最优参数，进而得到每个区域中的EAP。

限于篇幅，表1给出其中几个子区域的最优参数。

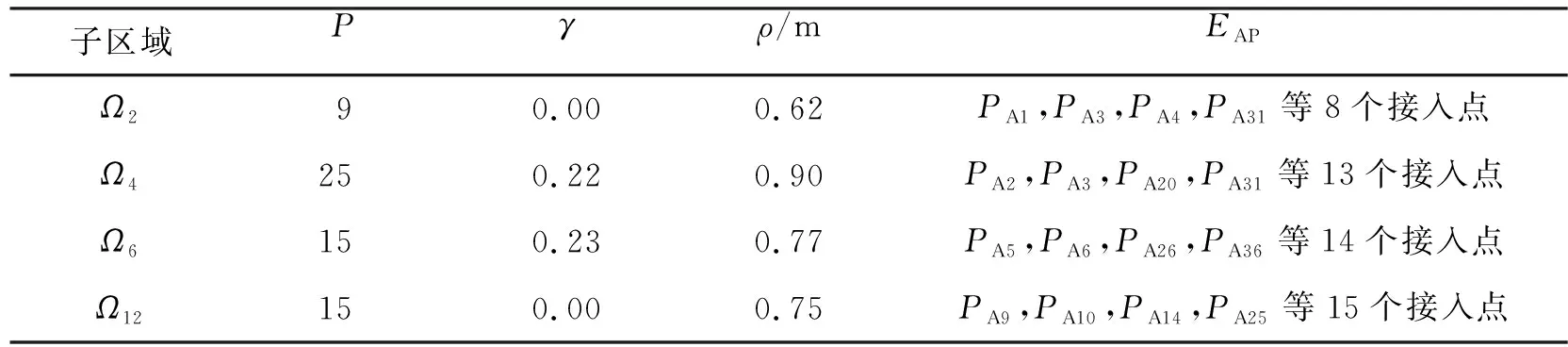
表1 代表性子区域内最优参数

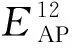
5.2.3 接入点精简效果分析

为验证笔者所提接入点选择策略的有效性，将EAP与MaxMean[7]、infoGain[8]、Fisher[9]3种接入点选择方法以及全接入点参与定位的贪婪方式进行对比实验。由于在整个测试场景中，|EAP|∈[3，15]，故3种接入点选择算法以3为最小值，15为最大值，在每个区域中寻找最佳接入点数量并提取相关接入点信息后进行比较运算。

定位误差分析如图6所示。笔者提出的在每个子区域中选取EAP的方式，在同等的误差范围内，均优于所有接入点均参与定位的定位结果。说明在噪声环境下，并不是所有的接入点信号均有利于定位。由于接入点信号的不稳定甚至某些接入点信号的缺失，离线阶段探测到的不良接入点特征参与定位运算将会加大误差。同时，由于MaxMean方法只选用子区域中均值较大的接入点信号，忽略了均值低但稳定的接入点信息，定位效果最差，平均定位误差达到了1.270 m；infoGain和Fisher未考虑接入点信号的稳定可见性，选用了某些在线阶段未探测到的接入点，定位精度提升有限，均值误差分别为1.140 m和1.182 m。而EAP在每个子区域中考虑接入点信号的稳定可见性，并去除了无关及冗余接入点，整体定位性能最优，平均误差仅为0.995 m，较MaxMean、infoGain、Fisher算法分别提升了21.7%、12.3%和15.8%。

5.2.4 接入点稳定性修正效果分析

如节3.2所述，针对传统欧氏距离只考虑在线数据与离线指纹整体相似度的局限性，提出利用接入点稳定性对欧氏距离进行修正，减少不稳定接入点信号所占的距离权重。为比较其对定位精度的影响，与无稳定性修正的定位结果进行了对比实验，结果如表2所示。

表2 接入点修正欧氏距离对定位误差的影响分析

可见，采用稳定性修正的整体定位效果最好，平均误差为0.977 m，较传统欧氏距离的0.995 m提高了约1.8%；同时，1 m之内的定位误差占比最高，说明利用区域中接入点稳定性修正度量的方法的确有利于提高定位的精度。在后续实验中，SAFC将采用接入点稳定性修正距离的方式进行对比运算。

5.2.5 速度约束效果分析

为使定位结果可信度更高，笔者提出基于速度约束筛选定位野值。其中浮动参数δ的取值越小，约束能力越强，但会造成较多待定位点无法给出确切位置，使得用户体验较差。结合定位性能与实验场景的整体需求，在当前场景环境中设定δ=1.5，m=5，此时基于速度约束剔除13个野值点。表3给出了δ=1.5时定位验证对定位误差的分析，证明了SAFC基于用户的移动速度对定位结果进行验证的可行性。

表3 定位验证对定位估计误差的影响(δ=1.5)

5.2.6 整体定位结果

为验证SAFC的整体性能，分别与DDWKNN[5]、AAS算法[18]以及传统的WKNN算法进行对比运算。实验中，所有算法的K=3，DDWKNN根据空间特征将聚类数目选为6。为保证测试数据的一致性，在SAFC中取δ=5，此时无定位野值从数据中滤除。

从图7可知，在对测试点估计位置时，在同等的误差范围内，SAFC均优于其他定位算法，其估计误差在1 m之内的数据占比达到了63.2%，而其他算法均不足55%。表4给出了4种定位算法的位置估计误差值，SAFC在误差平均值、最大值及方差值方面均优于其他定位方法。在整个定位环境中，其平均误差保持在1 m以内，达到了0.977 m，相比于WKNN，定位精度提升了约15.9%。这说明SAFC在复杂的室内环境中对定位结果的提升是全方面的。

6 结束语

针对复杂的室内定位环境，传统的聚类方法难以划分物理空间，且室内接入点数目繁多从而影响定位性能的问题，笔者提出了一种新的室内定位算法。该算法通过分析接入点信号总体的均值特征判定参考点所属区域，经双重筛选获取每个子区域中接入点的最佳辨识集，最后通过修正距离及速度后验的方式反馈定位位置，力求给用户最可信的定位结果。实验证明，所提算法在提高定位精度的同时，大大地减少了数据库中所需存储的数据量，在室内环境下具有较高的实用价值。