散体滑坡涌浪形成与传播的物理模拟试验研究

吴长虹，江兴元，2，杨 义，严 炎，任 意，王中美，2

(1.贵州大学 资源与环境工程学院，贵阳 550025； 2.贵州大学 喀斯特地质资源与环境教育部重点实验室，贵阳 550025；3.西南交通大学 土木工程学院，成都 610031)

1 研究背景

滑坡涌浪是滑坡入水引发的一种次生灾害，具有生成及传播历时短、速度快和致灾范围广等特征，近年来国内外滑坡涌浪造成的灾害事件频发。滑坡涌浪生成与传播过程中关键参数的获取是开展涌浪研究的关键。黄波林[1]通过龚家方崩塌视频资料获取涌浪最大高度，殷坤龙等[2]依据河道两岸植被冲蚀痕迹调查开展涌浪爬高研究。但事故分析调查往往也存在关键参数缺失或初始涌浪高度难以获取等问题。目前，基于室内物理模拟试验开展滑坡涌浪的生成、传播及爬高等过程研究是较为常用的方法。

滑坡诱发涌浪可划分为滑体完全入水和非完全入水2种类型，滑坡体是否完全入水不仅受到水深的影响，还与滑体规模和运动速度等指标密切相关[3]。在滑体完全入水触发涌浪波幅研究方面，Cui等[4]基于模型试验分别建立了初始涌浪和二次涌浪波高预测模型；殷坤龙等[5]改进了适用于宽水域条件下涌浪最大波幅预测模型；Huang等[6]借助室内涌浪模拟试验，建立了块状和散体滑坡涌浪波高预测模型；Wang等[7]优化了滑坡涌浪最大波幅预测模型；丁军浩等[8]开展了原型物理相似试验，提出了最大首浪高度的回归模型；赵永波[9]基于二维块体模型试验提出了浅水区滑坡涌浪的波高预测模型；韩林峰等[10]结合深水区与浅水区滑坡涌浪试验，基于动量守恒原理提出了最大近场波幅的预测模型。以上研究基于模型试验提出了涌浪浪高预测模型，但在滑坡体类型、规模、坡体淹没与水深等综合相关性方面缺乏深入阐述，预测模型的适用性方面存在一定局限性。

在涌浪波形研究方面，Noda[11]将涌浪波分为振荡波、非线性过渡波、类孤立波及涌波；Heller[12]结合涌浪波剖面特征、无量纲参数T和弗劳德数Fr的关系将涌浪分为类斯托克斯波、类椭圆余弦(或类孤立波)及涌波；岳书波等[13]通过试验观测涌浪初始形态及其演化过程，基于涌浪初始形态弗劳德数指标将涌浪波分为常规涌浪、推移涌浪和跃冲涌浪。然而以往的研究并没有区分完全入水滑坡涌浪和非完全入水滑坡涌浪形态的差异性，不同滑坡体规模、运动速度和水深等指标差异化条件下的涌浪形态研究还需要进一步加强。

为此，本研究设计了涵盖完全淹没与非完全淹没散体滑坡涌浪的物理模拟试验，重点观测不同条件下涌浪的波形特征，并提出基于单宽体积比和滑体运动速度指标的涌浪波形分类方法和波幅预测模型，为统筹兼顾深水区与浅水区滑坡涌浪预测提供参考。

2 试验设计

2.1 试验装置与材料

试验在贵州大学地质灾害模拟实验中心进行，装置由试验水槽、联合斜坡和滑体组成(图1)。水槽长5 m、宽0.75 m、高1.2 m，水槽侧面加装钢化玻璃并粘贴5 mm×5 mm透明网格纸用于涌浪观测，误差为±5 mm。斜坡滑面长2.6 m、宽0.6 m，两侧安装翼板，可变角、升降和移动；在斜坡对面和试验水槽侧面分别布置一台高清摄像机(佳能 EOS 6D)，像素2 020万，以30帧/s的速度记录滑体下滑及涌浪生成与传播过程。试验中1#摄像机布置于透明玻璃侧3 m范围内，架设高度与静水面齐平；2#摄像机布置于斜坡正面水槽顶部，以垂直滑面摄影的方式记录滑体下滑，其位置随滑面倾角与下滑高度变化而改变，但距滑面的距离不超过3 m。需要说明的是本研究仅观测首次涌浪过程，涌浪均未受到对岸反射波的影响。

图1 试验装置示意图Fig.1 Schematic diagram of the experimental equipment

滑体材料为白云岩碎石，粒径分别为5～10、10～20、20～50 mm的颗粒按质量比7∶2∶1配制，平均粒径d50=8 mm，滑体密度ρs=1.42 g/cm3，试验材料见图2。

图2 试验用材料Fig.2 Test materials

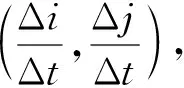
(1)

获取像素参数与实际位移比例关系，通过点阵视觉平面像素流速场换算，得到视觉平面xOy中的视觉投影流速场。软件获取的流速参数准确性高，精度可达0.01 m/s，已经在滑坡、泥石流等相关的室内物理试验及野外案例分析中得到应用和验证[14]。

2.2 试验方案

采用正交试验，考虑滑体体积Vs、滑面倾角α、下滑高度h0和水深h等指标(图3)，Vs通过调整料盒长宽厚来控制，α为30°～45°。一般认为水深<0.2 m时，试验存在尺寸效应[15]，故本次设计最小水深0.2 m，最大水深0.5 m。试验设计见表1，Vs为3水平，其余3因素为4水平，共计18组试验。图3中vs为滑体冲击速度；a为涌浪波峰振幅；at为波谷振幅；H为波高；b为水槽有效长度，是静水面与滑面交界处至对岸距离，由滑面倾角控制。

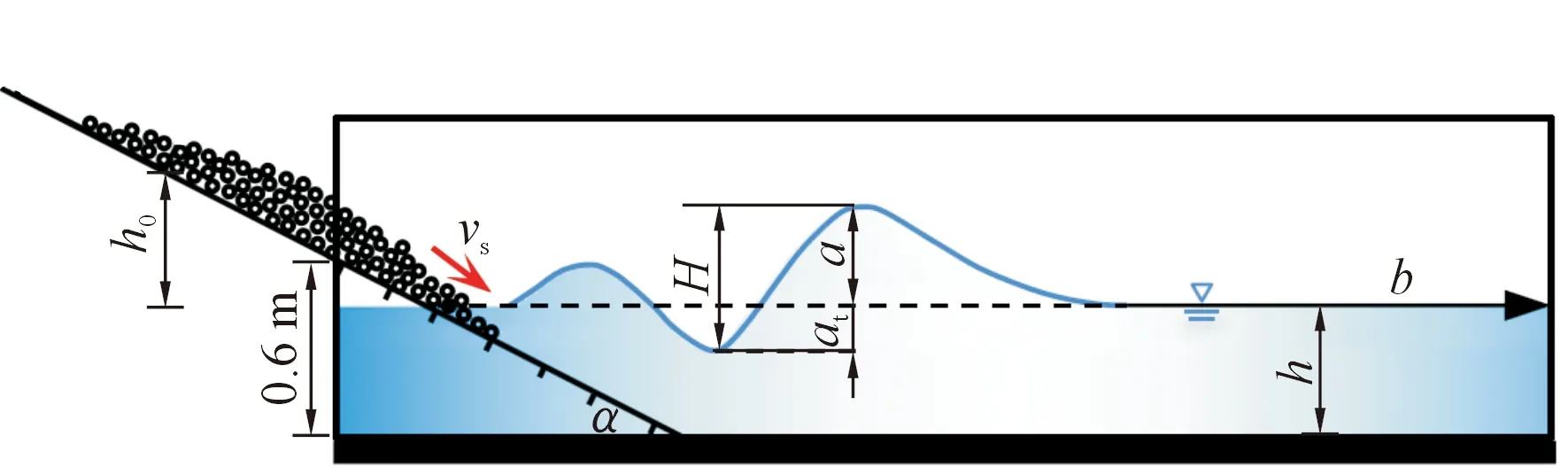
图3 各参数定义示意图Fig.3 Schematic diagram of the definition of parameters

表1 正交试验设计Table 1 Orthogonal experimental design

3 试验结果及分析

3.1 散体滑坡运动特征

滑体入水冲击速度是试验研究的关键指标。通过Debris Flow捕获滑体前缘10 cm范围内散体颗粒冲击静水面时的平均速度作为滑体冲击速度。以试验3为例，截取滑体冲击静水面前后相邻时刻的影像，获取滑坡速度场分布如图4所示。滑坡体呈“舌型”楔入水体，部分散体颗粒受模型边界影响，两侧滑速偏小，中间滑速大，散体入水冲击平均速度取1.49 m/s。

图4 滑坡速度场特征Fig.4 Characteristics of velocity field of landslide

3.2 涌浪特征

3.2.1 涌浪过程

试验观测到的涌浪可概括为水花团-首浪-后续涌浪3个过程。如图5所示，t=0 s时刻滑体前缘冲击静水面，生成水花并呈抛物线溅射出水面，见图5(a)。滑体迅速入水，占据和置换部分水体空间，扰动区水位壅高，倾向对岸；生成的水花团规模继续增加，并于t=0.13 s时水花团高度达到最大，见图5(b)。t=0.23 s时，水花团溅落回水面，生成稳定的首浪，见图5(c)。后续入水滑体不再生成较大的水花团，而是推动首浪脱离生成区迅速向前“逃逸”。t=1.33 s时，滑体完全停止运动，此时首浪已向前传播一段距离，后续涌浪相继生成，见图5(d)。

图5 涌浪过程Fig.5 Time series of surge wave

3.2.2 涌浪波形特征

试验中观测到的涌浪均具有稳定波形和较大波长，波峰振幅大于波谷，为非线性波，首浪波幅较后续涌浪波幅大。按照孤立波破碎准则[16]：a/h=0.78，相对波幅大于该值即为破碎波，低于该值则为稳定波。统计试验中相对最大波幅(Am=am/h)见图6，结果表明Am均小于临界值，说明试验生成的涌浪波均为非破碎波，与观测结果一致。

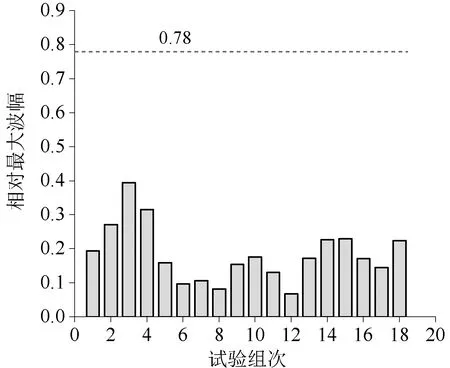
图6 试验组次对应的相对最大波幅Fig.6 Relative maximum wave amplitudes generated in each test

图7为试验中提取的典型涌浪波剖面。可将其分为两类：第一类多产生于滑体完全入水工况，具有波前平缓、波后较陡的特点，涌浪整体上关于竖直和水平轴对称，见图7(a)，首浪具有较大的波幅，后续涌浪波幅较小，波谷明显，涌浪呈“匍匐”态传播。第二类多产生于滑体未完全入水工况，较第一类涌浪波具有更明显的波峰，波形仅关于竖直轴对称，见图7(b)，首浪波幅较后续涌浪大，波谷不明显，仅有一个主波。该类涌浪波峰初始形态尖突，表明其相对波幅接近波浪破碎的临界值，随着涌浪传播，波形逐渐平滑稳定。在第二类涌浪波中发现试验3生成的涌浪波形较特殊，见图7(c)，其波谷消失，无后续涌浪生成，时空上表现为孤立波峰的传播，具孤立波特征。

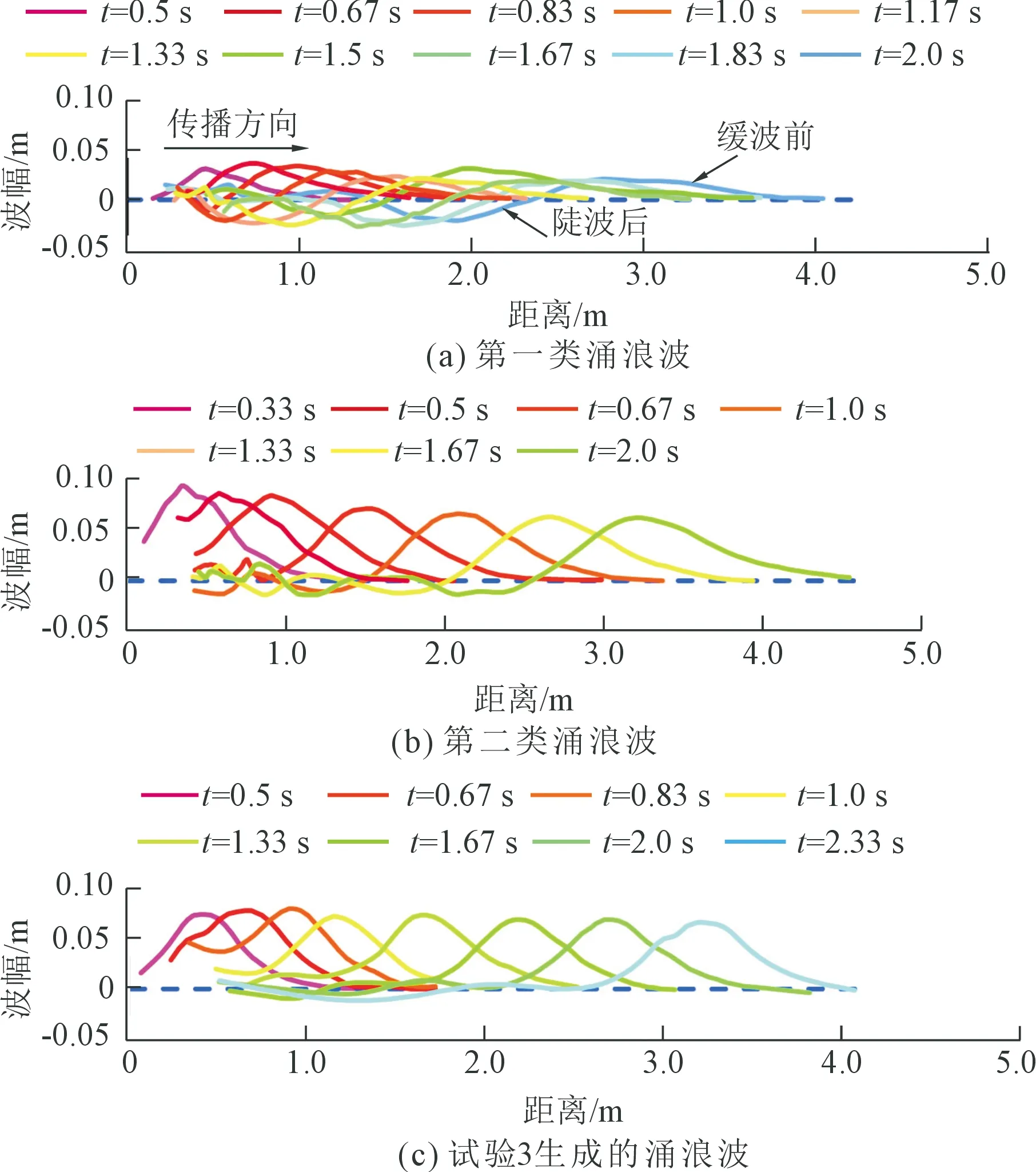
图7 涌浪波形演化Fig.7 Evolution of surge waveform over time with distance

整体上，这两类波形均无前导波谷，首浪均是基于静水面的爬升，波峰振幅在入水处附近迅速增加至最大值后衰减。所不同的是，在生成区第一类涌浪波首浪波峰后往往伴有一个振幅较大的波谷；而第二类涌浪波在生成区则是使水面明显壅高，波峰后无负振幅的波谷生成，其非线性强于第一类涌浪波，但随着涌浪传播距离和时间的增加，a/at逐渐减小，波谷越来越明显。

3.2.3 涌浪波形分类

Miller等[17]发现波形变化受滑体与水体规模影响。相对水体，较小的滑体生成的涌浪具有非破碎、稳定和波长较大的特点，反之则表现为破碎。Wang等[7]在三维试验中借助单宽体积比R用于涌浪波幅的预测，该参数能在一定程度上反映滑体与水体规模间的关系，本文尝试引入该参数作为波形分类的定量化指标，表达式为

(2)

式中：s为滑体厚度；l为滑体长度。

为区分涌浪波形态，Heller[12]定义了无量纲参数T，并根据参数T与弗劳德数Fr的关系，将涌浪波形态划分为类斯托克斯波、类椭圆余弦波(或类孤立波)和涌波3种类型，表达式为

T=S1/3Mcos[(6/7)α]。

(3)

式中：相对滑坡厚度S=s/h；相对滑坡质量M=ms/(ρwwh2)，ρw为水体密度，w为滑体宽度；弗劳德数Fr=vs/(gh)0.5，vs为滑体冲击速度，g为重力加速度。

图8为依据本次试验数据绘制的T-R关系(带误差棒)。无量纲参数T与单宽体积比R呈线性相关(r2=0.92)，说明基于单宽体积比R的波形分类具有可行性。

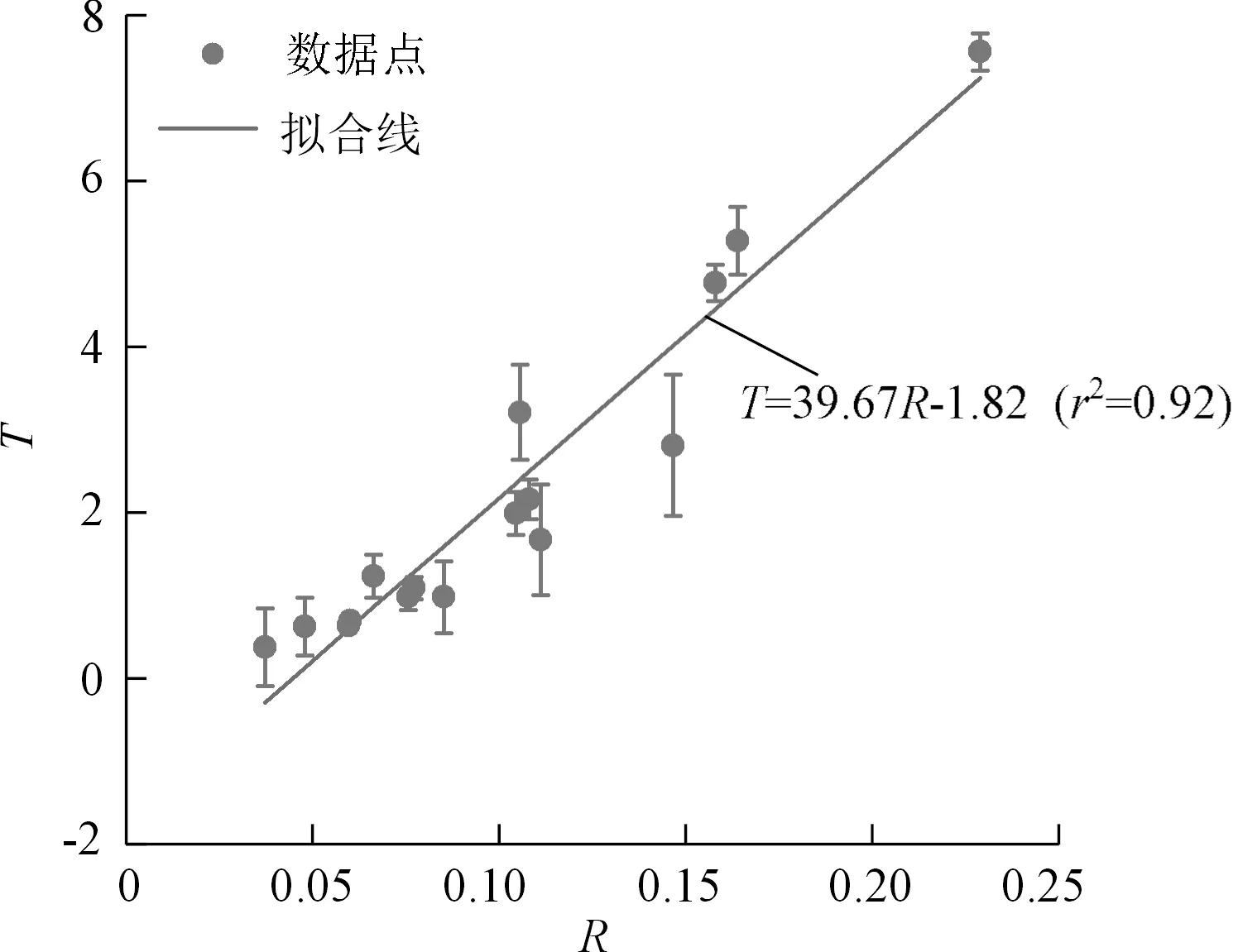
图8 T-R关系Fig.8 Relationship between T and R

图9为依据试验数据绘制的R-Fr关系进行的涌浪波形分类。图中黑色实心点为本次试验实测值，空心点为Heller[12]划分的涌浪波形。试验观测到的涌浪类型主要为类斯托克斯波和类椭圆余弦波(或类孤立波)，未见涌波。统计分析发现当满足R<0.02Fr-7/5+0.05时生成的涌浪为类斯托克斯波，当R>0.28Fr-5/2+0.05时形成涌波，介于两者之间形成类椭圆余弦波(或类孤立波)。从图9可进一步发现，随着Fr的增加，类椭圆余弦波(或类孤立波)的分类区间被不断压缩，涌浪更容易由类斯托克斯波转化为涌波，这需要满足R>0.05，否则，即使再大的Fr值也只能生成类斯托克斯波，而不会生成其他波形的涌浪，也就观测不到涌浪初始形态的变化。因此单宽体积比R和弗劳德数Fr是控制涌浪波形变化的两个关键性参数。

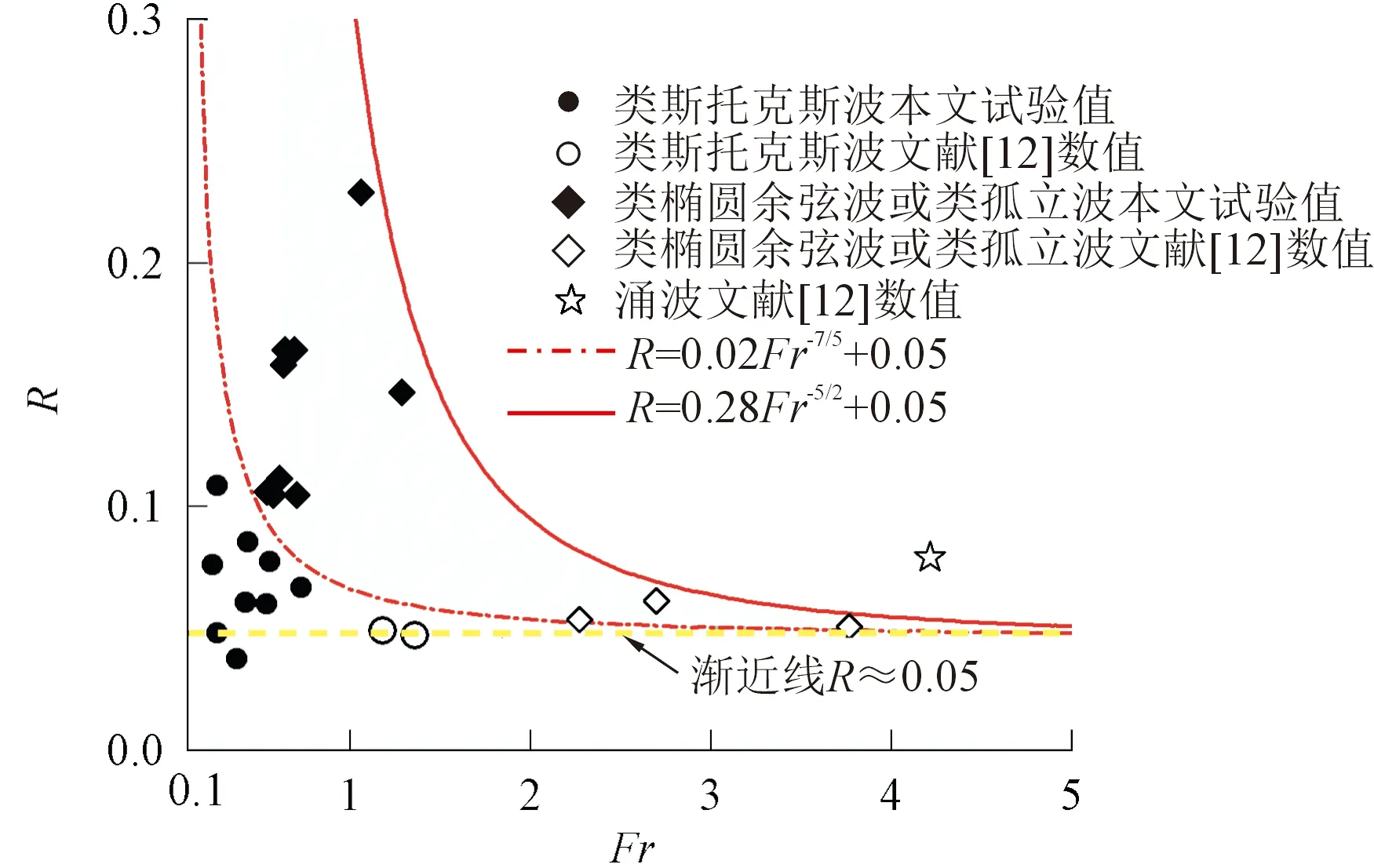
图9 基于R-Fr关系的涌浪波形分类Fig.9 Classification of wave types based on the relationship between R and Fr

3.3 涌浪最大波幅预测模型

3.3.1 相对最大波幅与R的相关性分析

图10给出了相对最大波幅Am与单宽体积比R的关系。结果表明，相对最大波幅与单宽体积比呈幂函数关系(r2=0.88)，表明单宽体积比R对涌浪波形和波幅均具有重要的影响。该参数表征滑坡体纵剖面面积与平行于此方向的水体概化面积之比，不仅反映了滑坡体积或质量的影响，同时也体现了相对滑坡厚度S=s/h和相对滑坡长度L=l/b的影响。

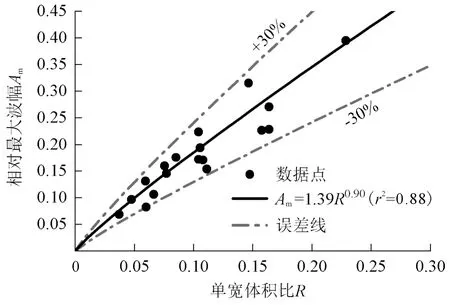
图10 相对最大波幅与单宽体积比的关系Fig.10 Relative maximum wave amplitude as a function of unit-width volume ratio

3.3.2 涌浪最大波幅预测

基于单宽体积比R，本研究提出涌浪最大波幅的3种预测模型为

式中的c1、c2、c3均为待定系数。

使用方差分析对比涌浪波幅的预测模型，结果见表2。结果表明式(6)的相关性(r2=0.902)最好，与实测值偏差较小，选定散体滑坡涌浪最大波幅预测模型为

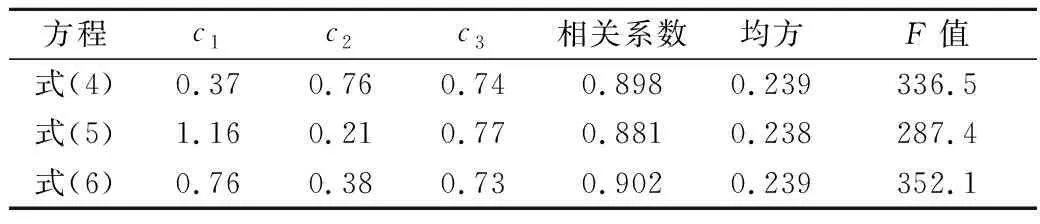
表2 方差分析Table 2 Analysis of variance

(7)

图11给出了由式(7)计算的相对最大波幅预测值与观测值的比较。从图11可看出预测值与观测值相对误差较小，平均相对误差在13.3%以内，拟合效果良好。

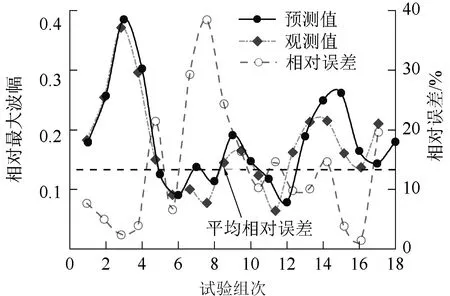
图11 观测值与预测值比较Fig.11 Comparison between observed test values and predicted values

3.3.3 实例验证

选取大堰塘滑坡、龚家方滑坡、千将坪滑坡和新滩滑坡涌浪案例来验证模型的适用性。前两者代表深水区完全淹没滑坡生成的涌浪，后两者为浅水区未完全淹没滑坡涌浪，浅水区滑坡涌浪波幅计算中R采用R=s/h代替[7]。相关参数和预测结果见表3。

表3 滑坡触发涌浪参数和预测结果Table 3 Parameters and prediction results of landslide-generated surge wave

结果显示模型预测值与滑坡涌浪实例吻合较好，大堰塘滑坡和龚家方滑坡最大波幅误差分别仅为0.6 m和0.3 m，相对误差较小，千将坪滑坡和新滩滑坡涌浪误差分别为4.5 m和4.1 m，相对误差在18%以内。进一步分析发现，基于本试验设计的18组模型试验，构建的涌浪波幅预测模型中的弗劳德数Fr∈[0.242，1.289]，符合大多数涌浪实例真实情况，而单宽体积比R∈[0.037，0.229]，模型适用范围稍窄，对于具有较大单宽体积比的浅水区滑坡涌浪，模型预测效果还有待于进一步的修正，后期笔者会进一步补充和开展相关试验研究。

4 结 论

研究基于深水区与浅水区滑坡涌浪开展物理模拟试验，探究了2种条件下滑坡涌浪的波形与波幅特征，提出了涌浪波形分类方法及最大波幅预测模型，得到如下结论：

(1)试验观测到深水区滑坡涌浪首浪波幅较大，波谷明显，波形具有波前平缓、波后较陡的特点，关于竖直和水平轴对称，涌浪呈“匍匐”态传播；浅水区滑坡涌浪首浪波幅明显大于后续涌浪波幅，无明显波谷，仅有一个主波，波形关于竖直轴对称，但随着涌浪传播，波谷越来越明显。

(2)提出了R-Fr波形分类方法，根据此方法可将涌浪分为3种类型：R<0.02Fr-7/5+0.05，形成类斯托克斯波；0.02Fr-7/5+0.05≤R≤0.28Fr-5/2+0.05，形成类椭圆余弦波(或类孤立波)；R>0.28·Fr-5/2+0.05，形成涌波。而R=0.05是涌浪波形发生转化的临界值。

(3)使用R-Fr波形分类方法对本次观测到的涌浪进行了划分。在试验范围内，发现深水区滑坡涌浪多为类斯托克斯波，浅水区滑坡涌浪一般为类椭圆余弦波(或类孤立波)。

(4)建立了涌浪最大波幅预测模型，并与真实案例进行比较，模型能够较好地预测深水区滑坡涌浪，平均相对误差仅2.5%；与浅水区滑坡涌浪实例误差在18%以内，这与本试验设计单宽体积比参数取值范围稍小有一定的关系，下一步计划扩宽试验参数范围开展全组试验。