大理岩球砾循环加卸载接触力学特性试验研究
马文俊,曾亚武,叶 阳
(武汉大学 土木建筑工程学院,武汉 430072)
1 研究背景
堆石料由于其廉价易得以及众多优良的工程特性而得到广泛应用,如水库土石坝、铁路道砟、跨江大桥墩台等。堆石料在细观尺寸上是由众多的堆石颗粒构成的集合体,受载过程中单个堆石颗粒的力学性质直接影响着堆石料的宏观力学行为,结构整体的失稳破坏也往往源于局部堆石颗粒的变形破碎。并且在实际工程中,堆石料往往承受循环加卸载,而不是单一的静荷载。因此,开展堆石颗粒在循环加卸载条件下的力学特性研究,有利于分析预测结构整体的变形与稳定,对土石坝、有砟轨道等工程建设具有重要的指导意义。
目前,国内外学者通过大型三轴试验对循环荷载作用下堆石料的力学特性研究已取得丰富成果,对堆石料阻尼比和残余变形的变化规律形成一定的共识[1-4]。堆石料集合体的能量损耗以及残余变形是堆石颗粒耗能和不可逆变形的累积效应,厘清堆石颗粒个体的力学特性,才能更加深入地探究堆石料的宏观力学性质。
截至目前,已有许多关于颗粒压缩破碎过程的研究[5-7],主要涉及颗粒破碎强度的分布规律和影响因素。然而实际工程中,堆石颗粒往往是在多次加卸载后,力学性质不断劣化,最终产生破碎。为此,部分学者采用单颗粒开展了循环加卸载试验研究,其中Mader-Arndt等[8]发现循环加卸载会导致颗粒力学性质发生明显变化,并指出这种变化与颗粒接触区域的致密化变形直接相关;Antonyuk等[9]针对颗粒开展加卸载试验,研究了颗粒的接触刚度、接触半径和能量耗散等接触力学性质的变化规律;Gilson等[10]研究了麦芽糖糊精颗粒的循环加卸载硬化现象,发现颗粒的弹性模量和屈服强度在循环加卸载过程中增加到一定值后保持不变;Weis等[11]则建立了一种球形颗粒循环加卸载模型,并通过加卸载试验验证了模型的有效性。上述研究多以食品、药品生产加工中的颗粒为研究对象,颗粒直径较小,在颗粒材料属性和尺寸方面与堆石颗粒仍存在较大的差距。
本文采用直径为60 mm的大理岩球形颗粒(球砾),分别开展压缩破碎试验、准静态循环加卸载试验和动态循环加卸载试验,探究大理岩球砾在循环加卸载过程中的力学特性及其变化规律,包括变形特征、接触刚度、能量耗散特性、阻尼比等,以及相应的变化规律。
2 Hertz弹性接触理论
Hertz[12]提出,相对较软的球形颗粒和光滑坚硬平面发生弹性接触时,接触区域呈圆形,接触区域的应力分布呈半椭球形,并据此导出了两球体弹性接触时法向接触力Fel和法向位移s之间的关系,即
(1)
式中:R*为两个弹性体的等效接触半径(mm);E*为等效弹性模量(GPa)。由于试验机刚性加载板的弹性模量和曲率半径均远大于大理岩球形颗粒,E*、R*计算式如下:
(2)
(3)
式中:E1、v1分别是大理岩的弹性模量(GPa)和泊松比;E2、v2分别是刚性加载板的弹性模量(GPa)和泊松比,E2=209 GPa,v2=0.31;R1、R2分别是大理岩球砾和刚性加载板的曲率半径(mm)。试验过程中对大理岩球形颗粒(球砾)进行法向压缩时,存在两个接触点,测得位移s是两个接触点间法向位移的总和,所以将s/2代入式(1)得到大理岩球砾静态加载时的力-位移关系,即
(4)
式中d1是大理岩球砾的直径(mm)。式(4)对位移s求导数,得到颗粒与加载板之间的弹性法向接触刚度kel(kN/mm),即
(5)
3 试样制备及试验方法
3.1 试样制备
试验采用的大理岩球砾矿物颗粒细小并且均匀,所有的大理岩球砾均出自同一块大理岩荒料,确保试样力学参数的一致性。试验使用的大理岩球砾直径为57.94±0.50 mm,其基本力学参数见表1。

表1 大理岩球砾基本力学参数Table 1 Physical parameters of marble sphere
3.2 试验方法
为研究大理岩球砾的法向接触力学特性,分别开展了压缩破碎试验、准静态加卸载试验和动态循环加卸载试验。上述系列压缩试验均在武汉大学RMT-301岩石与混凝土力学试验系统上完成,如图1所示。

图1 试验装置Fig.1 Compression testing device
首先开展大理岩球砾压缩破碎试验,通过试验确定球砾的峰值荷载、屈服力、屈服位移等重要参数,为后续的循环加卸载试验方案制定提供依据。压缩破碎试验采用位移控制模式,斜坡加载,加载速率0.01 mm/s,采用5个试样开展重复试验。
其次开展大理岩球砾准静态循环加卸载试验,该试验是本文研究的重点。大理岩球砾准静态加卸载试验采用力控制模式,试验过程分成2个阶段:先斜坡加载至荷载均值,加载速率0.10 kN/s;然后采用正弦波加卸载,加载频率为0.01 Hz。
最后开展大理岩球砾动态循环加卸载试验,研究动态循环荷载对大理岩球砾力学特性的影响。大理岩球砾动态循环加卸载试验加载方式与准静态加卸载试验相同,但加卸载频率为1.00 Hz。
4 试验结果及分析
4.1 压缩破碎试验结果及分析
大理岩球砾压缩破碎试验力-位移曲线如图2所示,作为比较,将由式(4)计算得到的Hertz弹性曲线也示于图中。初始加载时接触面分布应力小于屈服强度,球砾产生弹性变形。当加载至F点时接触面中心的应力率先达到屈服强度,若继续加载,接触面中心圆形区域的应力均达到屈服强度,产生塑性变形,而接触面边缘的环形区域内应力仍小于屈服强度,发生弹性变形,此阶段弹性变形和塑性变形同时存在[9]。F点称为屈服点,是Hertz弹性曲线与试验力-位移曲线发生偏离的起始点,同时也是大理岩球砾弹性变形和弹塑性变形的分界点。此外,由式(4)知球砾发生弹性变形时F2与s3呈线性关系,可以由F2-s3曲线的直线段确定屈服点和等效弹性模量[13]。对于接触刚度在屈服点发生陡降的颗粒材料,还可以通过接触刚度的变化来判断屈服点[14]。
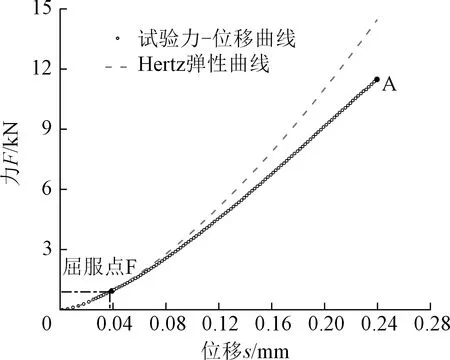
图2 大理岩球砾压缩破碎试验力-位移曲线Fig.2 Curve of compression crushing force versus displacement of marble spheres
根据试验结果,获得试验所用直径60 mm大理岩球砾的屈服力平均值为0.82 kN,破碎力平均值为14.80 kN,屈服力为破碎力的5.54%;屈服位移平均值为0.035 mm,破碎位移平均值为0.311 mm,屈服位移为破碎位移的11.30%。屈服点对应的力和位移相对于球砾压缩破碎时的力、位移都比较小,说明大理岩球砾在压缩试验过程中,纯弹性变形阶段存在时间很短,只在加载初期存在,随荷载增加,很快便进入弹塑性变形阶段,弹塑性变形处于主导地位。
大理岩球砾的破碎形态如图3所示,施加的法向荷载超出大理岩球砾的峰值破碎强度后,球砾沿经线平面发生脆性破坏,形成2个半球体(图3(a)),高度的应力集中导致接触区域形成两个锥形压缩破坏区(图3(b))。脆性颗粒压缩破碎试验中,往往认为是垂直于经线平面的拉应力导致了颗粒的宏观破碎[15]。

图3 大理岩球砾压缩破碎形态Fig.3 Failure patterns of marble spheres
接触刚度就是力-位移曲线的斜率,将整个力-位移曲线划分成50段,对每一段做线性拟合,其斜率可代表该段曲线的平均接触刚度[14],据此得到大理岩球砾的试验接触刚度-位移变化曲线,如图4所示,图中弹性接触刚度变化曲线由式(5)计算得到。由图4可见,随着位移增加,力-位移曲线的斜率增大,接触刚度增大;在屈服点以前,大理岩球砾的压缩试验接触刚度与Hertz模型计算的结果相同;超出屈服点之后,由于塑性变形的产生,球砾的压缩试验接触刚度小于相同位移下的弹性接触刚度(Hertz模型计算结果),并且随着位移的增加差值逐渐增大。
4.2 准静态循环加卸载试验结果及分析
本文准静态循环加载试验设定的下限荷载均为0.50 kN,而上限荷载分别为试验用大理岩球砾破碎荷载平均值(14.80 kN)的30%(4.44 kN)、50%(7.40 kN)、70%(10.36 kN)和90%(13.32 kN)。大理岩球砾准静态循环加卸载试验共4组,每组试验采用5个试样开展重复试验,每个试样准静态循环加卸载最多30次。试验过程中大理岩球砾平均变形速率最大为0.003 mm/s,可视为准静态加载。试验研究了大理岩球砾在准静态循环荷载作用下的变形规律、接触刚度变化规律和等效恢复系数变化规律等。
4.2.1 变形规律
图5(a)为上限荷载13.32 kN时试样各循环的力-位移曲线。由图5(a)可见,各循环加载曲线与卸载曲线都不重合,这是由于大理岩球砾在加载过程中产生了塑性变形,而加载曲线与卸载曲线围成的面积大小就是球砾由于塑性变形耗散的能量。观察各循环加卸载曲线,第1循环的力-位移曲线所围成的面积以及卸载后的残余变形都远大于其他各循环;随着循环加卸载次数增加,加卸载曲线围成的面积逐渐减小,塑性变形也逐渐减小。经过11次循环加卸载后,试样的加载曲线与卸载曲线几乎重合,产生的残余变形也非常小;经过23次循环加卸载后,加载曲线与卸载曲线基本重合,产生的塑性位移也难以分辨,此时累计塑性位移达到稳定值。
图5(b)为大理岩球砾准静态循环加卸载产生的弹性位移和塑性位移随循环次数的变化曲线。弹性位移整体上随循环次数增加而减小,前4次加卸载降低比较明显,但总体来说变化不大。塑性位移整体上随循环次数增加先迅速减小,然后逐渐趋近于0,尤其第1次循环加卸载产生的塑性位移占球砾累计塑性位移的80%以上。上述结果表明上限荷载不变时准静态加卸载循环次数对试样的弹性变形影响甚微,而对试样的塑性变形影响较大。塑性变形随加卸载循环次数增加而迅速减小的结果体现了大理岩球砾的循环硬化特性,球砾的循环硬化是由接触区域微观结构的改变所引起的,接触面分布的高压应力导致接触区域的微观结构发生巨大改变。

图5 准静态循环加卸载球砾曲线Fig.5 Curves obtained from quasi-static cyclic loading and unloading tests
针对图5(b)中塑性位移随循环次数变化曲线,采用模型spl,z=spl,1/zα能较好地描述塑性变形的发展规律[9],其中spl,z是第z次加卸载产生的塑性位移(mm),spl,1是第一次加卸载产生的塑性位移(mm),参数α与材料本身的性质以及外荷载的强度有关。大理岩球砾经过z次加卸载后的累计塑性变形等于各循环残余变形的总和,即
(6)
图6为不同上限荷载下大理岩球砾累计塑性位移随加卸载次数变化的试验结果及式(6)计算的理论曲线。由图6可知,上限荷载越大,大理岩球砾的累计塑性变形越大。通过试验结果拟合,上限荷载分别为4.44、7.40、10.36 、13.32 kN时,对应的α值分别为3.20、2.95、2.88、2.85,α值随着上限荷载的增大而减小,表明上限荷载越大,累计塑性变形达到稳定值所需的加卸载循环次数越多。
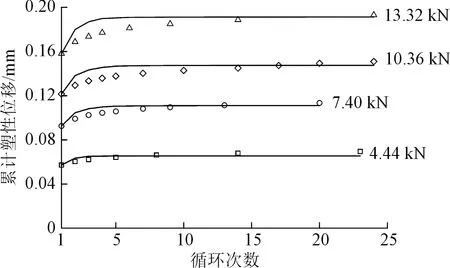
图6 准静态循环加卸载球砾累计塑性位移发展曲线Fig.6 Curves of cumulative plastic displacement along with the proceeding of cyclic loading and unloading
4.2.2 接触刚度变化规律
为研究准静态加卸载循环次数对大理岩球砾接触刚度的影响,计算力-位移曲线各段的平均接触刚度,得到每循环加卸载的接触刚度-位移曲线,如图7所示。大理岩球砾的接触刚度在第1次循环加载时随位移增加而非线性增大的特征十分明显,随后各循环加载时的接触刚度随位移增加而非线性增大的特征越来越不明显,经过几个循环后,逐渐变为直线增大。相同位移下接触刚度随循环次数的增加而增大,说明循环加卸载能显著增加大理岩球砾的接触刚度。第一次加卸载之后接触刚度增幅最大,之后增幅逐渐减小。经过15次循环的加卸载后,各循环的接触刚度-位移曲线基本重合,接触刚度随循环次数变化幅度很小,而只与当前循环的位移有关。
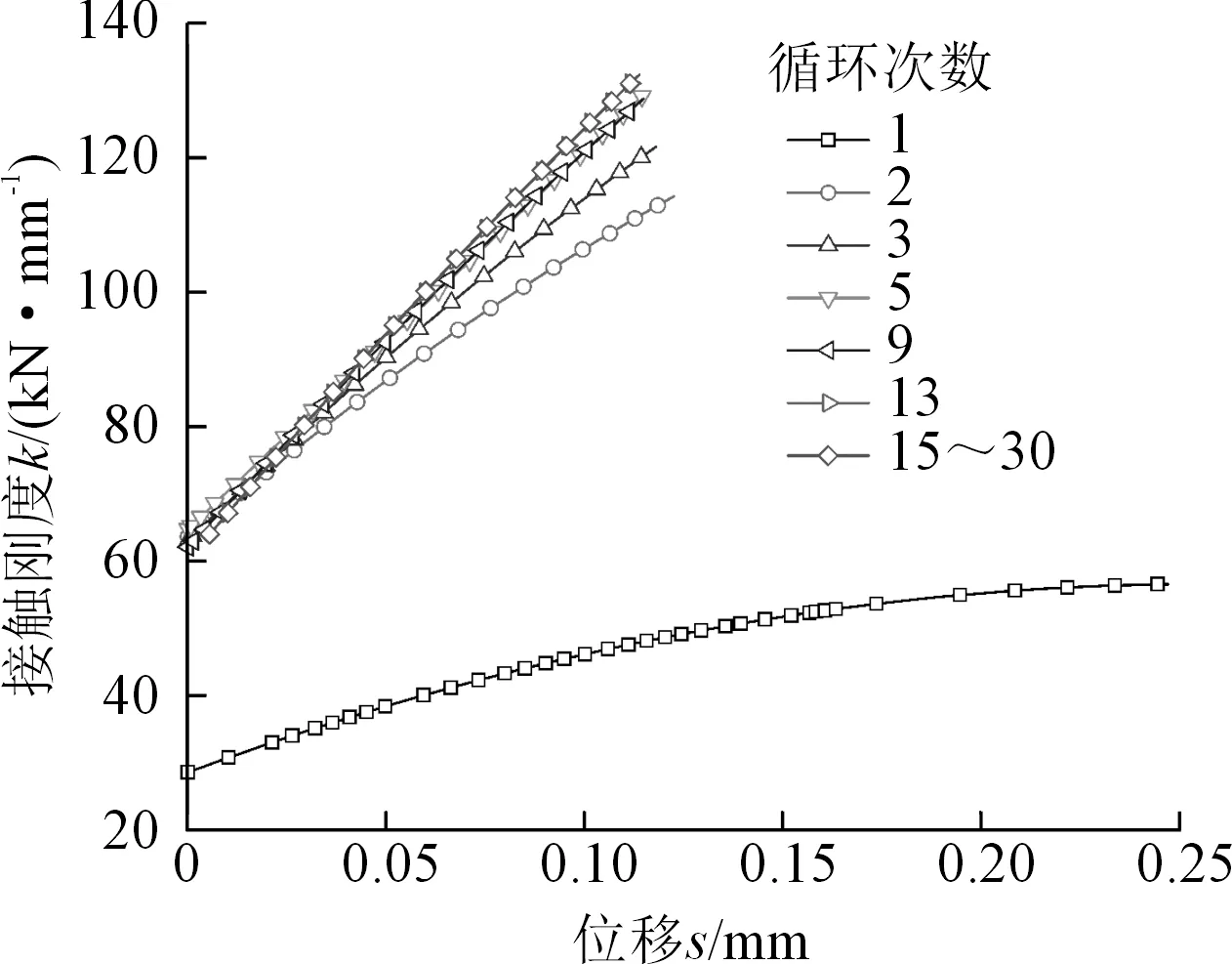
图7 准静态循环加卸载球砾接触刚度-位移曲线Fig.7 Curves of contact stiffness versus displacement in different cycles of loading and unloading
4.2.3 等效恢复系数变化规律
能量耗散是岩石破坏的本质属性,能量的变化能够反映岩石从受荷载开始到内部孔隙压密、裂隙出现、演化直至破坏的全过程。大理岩球砾在准静态循环加卸载过程中的能量吸收能力可以用等效恢复系数eeq来定量表示[16],等效恢复系数等于卸载过程中释放的弹性变形能Wel与加载过程总变形能WL比值的平方根,即
(7)
式中WL、Wel分别等于法向荷载在加载和卸载过程中所做的功(J)。
大理岩球砾在13.32 kN上限荷载条件下循环加卸载的等效恢复系数、总变形能以及弹性变形能与循环次数的关系如图8所示。观察到弹性变形能曲线近似水平,不随循环次数发生改变,这与图5(b)中弹性变形的变化趋势相同。总变形能在第1次循环加卸载后迅速下降,随后缓慢减小,逐渐向弹性变形能曲线靠近。总变形能和弹性变形能的差值就是大理岩球砾因塑性变形损耗的能量,塑性变形耗能的减小导致总变形能的下降。由于弹性变形能较为稳定,等效恢复系数具有与总变形能相反的变化趋势,对大理岩球砾反复加卸载会导致恢复系数的增加,直至达到稳定值。Weir和Tallon[17]对铜球颗粒进行了低速率法向碰撞试验,发现铜球的法向恢复系数也具有相同的变化趋势。
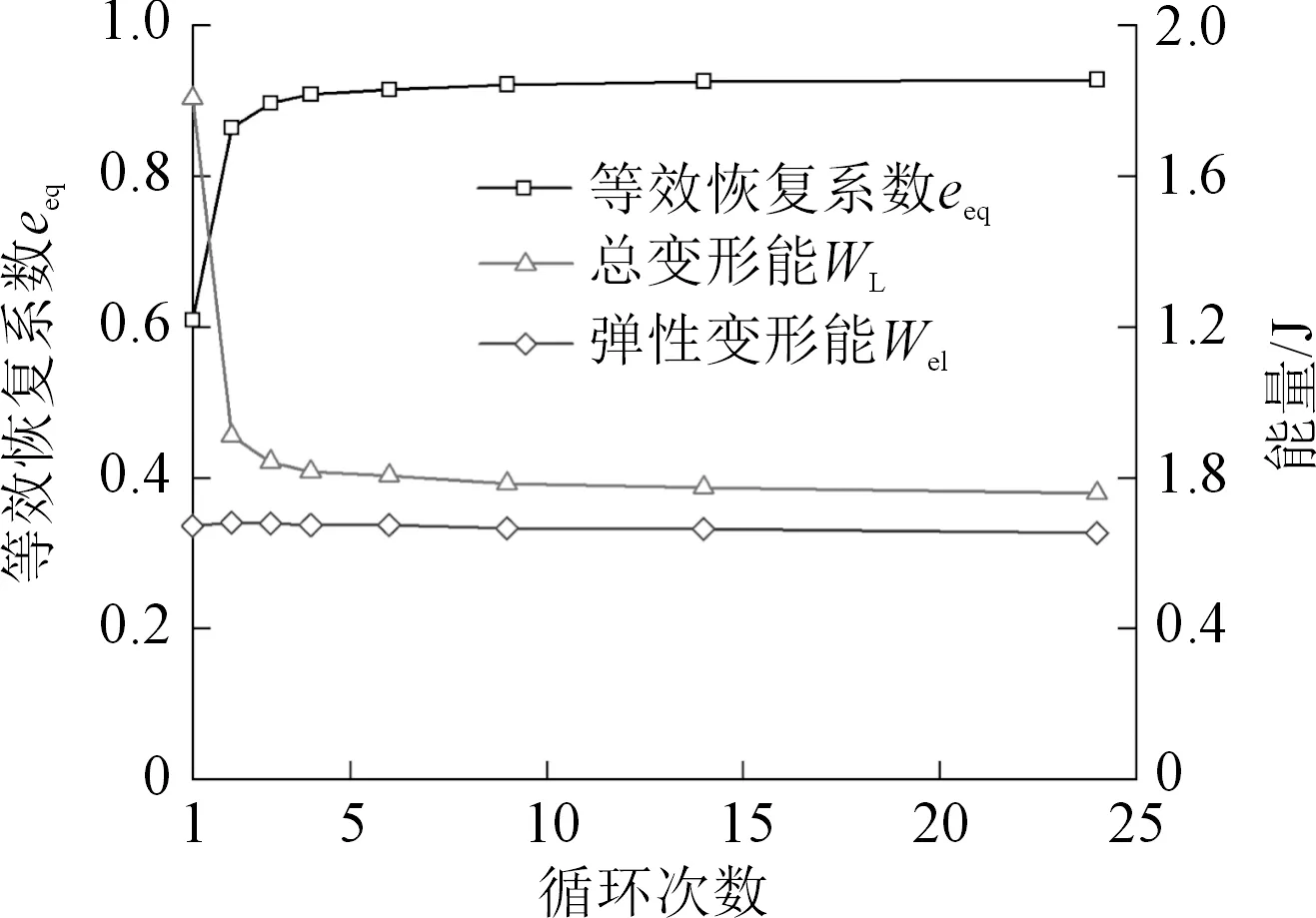
图8 等效恢复系数及变形能随循环次数变化关系Fig.8 Relation of equivalent restitution coefficient and deformation energy against the number of cycles
为研究上限荷载对球砾等效恢复系数的影响,分别选取第1次循环、第5次循环和第14次循环加卸载的等效恢复系数随上限荷载的变化曲线进行比较,结果如图9所示。由图9可见,第1次循环加卸载的等效恢复系数随上限荷载的增加而明显减小,表明上限荷载越大,球砾吸收的能量越多,也更容易积累损伤产生破碎。第5次循环和第14次循环的等效恢复系数随上限荷载增大而略有减小,说明经过若干次循环后,上限荷载对球砾等效恢复系数的影响较小,尤其第14次循环加卸载的等效恢复系数对应上限荷载从小到大分别为0.945、0.944、0.938和0.936,几乎相等,说明即使上限荷载有很大不同,加卸载一定次数后等效恢复系数会趋于相同的稳定值,因此可以利用等效恢复系数的上述变化特点来预测不同上限荷载下的等效恢复系数。
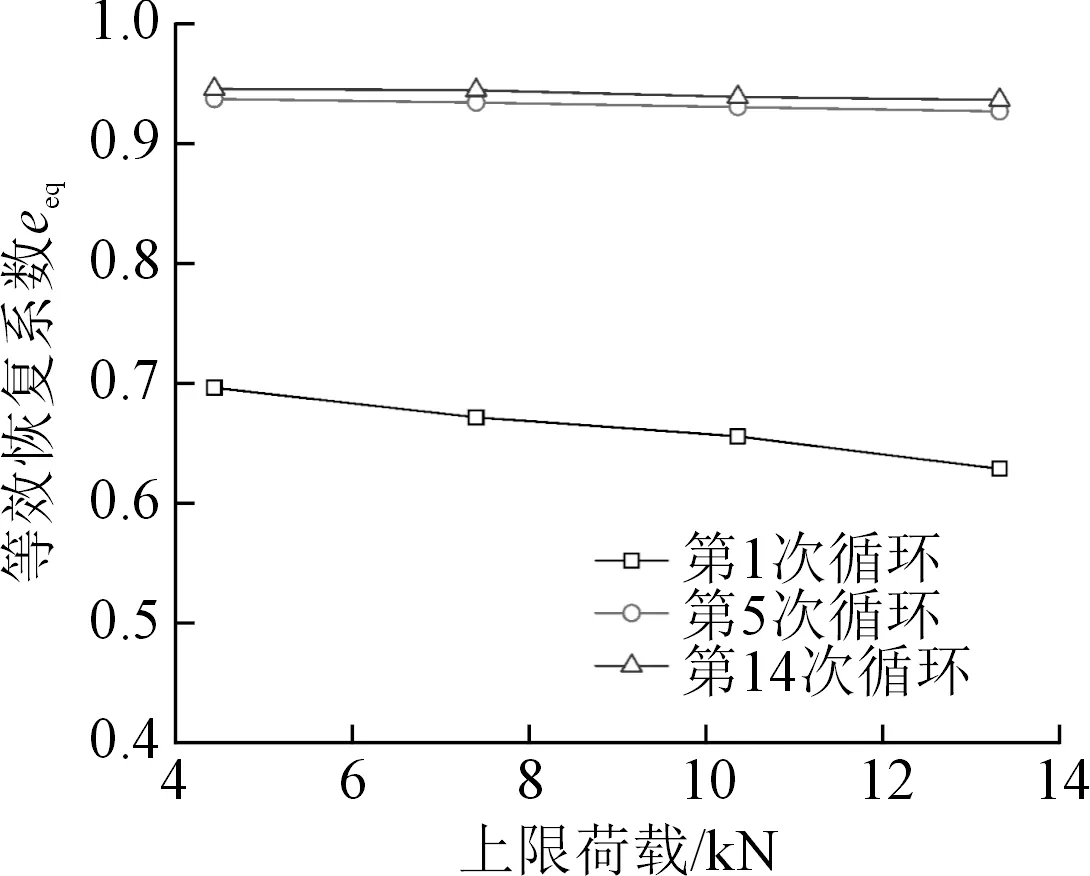
图9 准静态加卸载球砾等效恢复系数-上限荷载曲线Fig.9 Effect of upper limit load on equivalent restitution coefficient under quasi-static test
4.3 动态循环加载试验结果及分析
大理岩球砾动态循环加卸载试验,根据加载路径不同,分别开展了振幅保持不变而上限荷载不同的试验和上限荷载保持不变而振幅不同的试验。对于前者,试验方案为保持振幅为50%的平均破碎荷载(7.40 kN)不变,上限荷载分别为平均破碎荷载的60%(8.88 kN)、70%(10.36 kN)、80%(11.84 kN)和90%(13.32 kN);对于后者,试验方案为保持上限荷载为85%平均破碎荷载(12.58 kN)不变,振幅分别为平均破碎荷载的50%(7.40 kN)、60%(8.88 kN)和70%(10.36 kN)。大理岩球砾动态循环加卸载试验共7组,每组试验采用5个试样开展重复试验,每个试样动态循环加卸载最多2 000次。主要研究了大理岩球砾在动荷载作用下的塑性变形演化特征及阻尼比变化规律等。
4.3.1 塑性变形演化特征
大理岩球砾在动荷载作用下塑性变形的大小、增长速率及累积变形量能够更本质地反映其力学性能劣化、损伤过程。葛修润等[18]在开展周期荷载作用下岩石试样疲劳变形特性试验研究时,认为岩石的轴向变形演化具有三阶段发展规律,即初始阶段、等速阶段和加速阶段。大理岩球砾的累计塑性变形演化也具有类似规律,图10为大理岩球砾动态循环加卸载试验中出现的3种典型的累计塑性位移随循环次数的演化曲线。当上限荷载和荷载幅值较低(上限荷载8.88 kN,荷载幅值7.40 kN)时,大理岩球砾随动荷载循环次数增加而产生的累计塑性变形经过初始阶段的积累后,很快(约30次荷载循环)进入等速变形阶段,此后塑性变形缓慢增长,增长速率几乎保持不变,在本文试验最大循环加卸载次数内,没有出现加速阶段,即球砾没有破碎,累积塑性变形曲线只有2个阶段。当上限荷载很高(上限荷载13.32 kN,荷载幅值7.40 kN)时,球砾在加载初期直接进入加速阶段,经过几个荷载循环即发生破碎,累积塑性位移演化曲线只有一个阶段——加速阶段。这2种形式可以看作三阶段曲线的特殊情况[18]。当上限荷载和荷载幅值较大(上限荷载12.58 kN,荷载幅值8.88 kN)时,球砾累积塑性变形曲线在进入等速阶段(约40次荷载循环)后,随着塑性变形的累积,很快便进入加速阶段,球砾破碎(荷载循环次数约110次),此时球砾的累积塑性变形曲线呈现典型的三阶段特征。

图10 动态循环加卸载球砾累计塑性变形演化曲线Fig.10 Evolution of cumulative plastic deformation under dynamic cyclic loading
在大理岩球砾累积塑性变形演化曲线的初始阶段,曲线上凸,塑性变形增加较快,但变形速率逐渐减小,这一阶段大理岩球砾内部的薄弱位置迅速产生大量微裂纹,在微裂纹数量达到稳定后进入等速阶段;等速阶段位移曲线近似直线,累计塑性位移缓慢增加,此时微裂纹稳定扩展;当裂纹扩展到临界长度彼此贯通时,累计塑性位移曲线进入加速阶段,曲线陡然攀升,速率迅速增大,球砾发生破碎。等速阶段占据了疲劳周期的大部分时间,是疲劳寿命的主要部分,但是此阶段积累的变形量最小,而初始阶段和加速阶段在疲劳寿命中所占的比重很小,产生的累积塑性变形却大得多。
4.3.2 上限荷载和荷载幅值对塑性变形的影响
动态循环加卸载试验中,上限荷载以及荷载幅值对大理岩球砾的塑性变形有显著的影响。荷载幅值固定(7.40 kN)而上限荷载不同时累计塑性变形随循环次数的变化关系如图11所示,由于上限荷载为13.32 kN时已经接近平均破碎荷载,经过少数荷载循环球砾便突然破碎,故图11中只给出了上限荷载分别为8.88、10.36、11.84 kN的试验结果。由图11可见,荷载幅值固定而上限荷载不同时,球砾的塑性位移演化曲线具有相似性,但曲线的累计变形量相差较大,尤其是初始阶段各循环产生的塑性变形相差明显,即上限荷载越大,初始阶段各循环产生的塑性位移越大,累积变形曲线的斜率也越大,塑性变形增长速率更快,达到等速阶段所需的循环次数更多。进入等速阶段后,各曲线塑性变形速率相近。上述结果表明,若只考虑球砾累积塑性变形演化曲线的初始阶段和等速阶段,施加动荷载时的上限荷载(幅值固定)主要影响大理岩球砾在初始阶段的变形量和经历的循环次数,而进入等速阶段后对塑性变形率的影响较小。
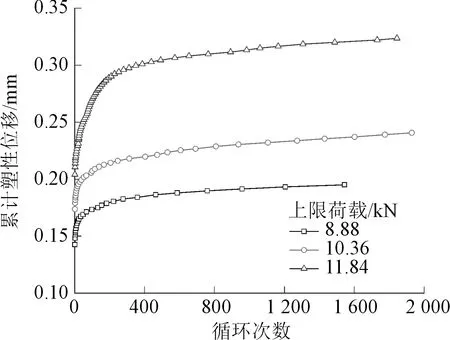
图11 荷载幅值为7.40 kN时不同上限荷载累计塑性 变形随循环次数变化Fig.11 Variation of cumulative plastic displacement with the number of cycles under different upper limit loads
图12为上限荷载固定(12.85 kN)而荷载幅值不同时累计塑性变形随循环次数的变化曲线。试验荷载共有7.40、8.88、10.36 kN 3种幅值,但幅值为10.36 kN时球砾只经过少数几个循环就发生破碎,故图12中只给出了荷载振幅为7.40、8.88 kN时的试验结果。由图12可见,前15次循环内2种荷载幅值下的累积塑性位移增长都很快,速率相近,但量值有差别;随后两者间的差距逐渐增大,荷载幅值越大,累积塑性变形增长越快;经过300次循环加载后,2条曲线都先后进入等速阶段,变形速率再次接近。对比图12中的2条曲线,发现荷载幅值越大,产生的塑性变形越大,变形稳定(进入等速阶段)所需的循环次数也越多。荷载幅值大小主要影响初始阶段的塑性变形量,而对等速阶段的塑性变形速率影响不大。
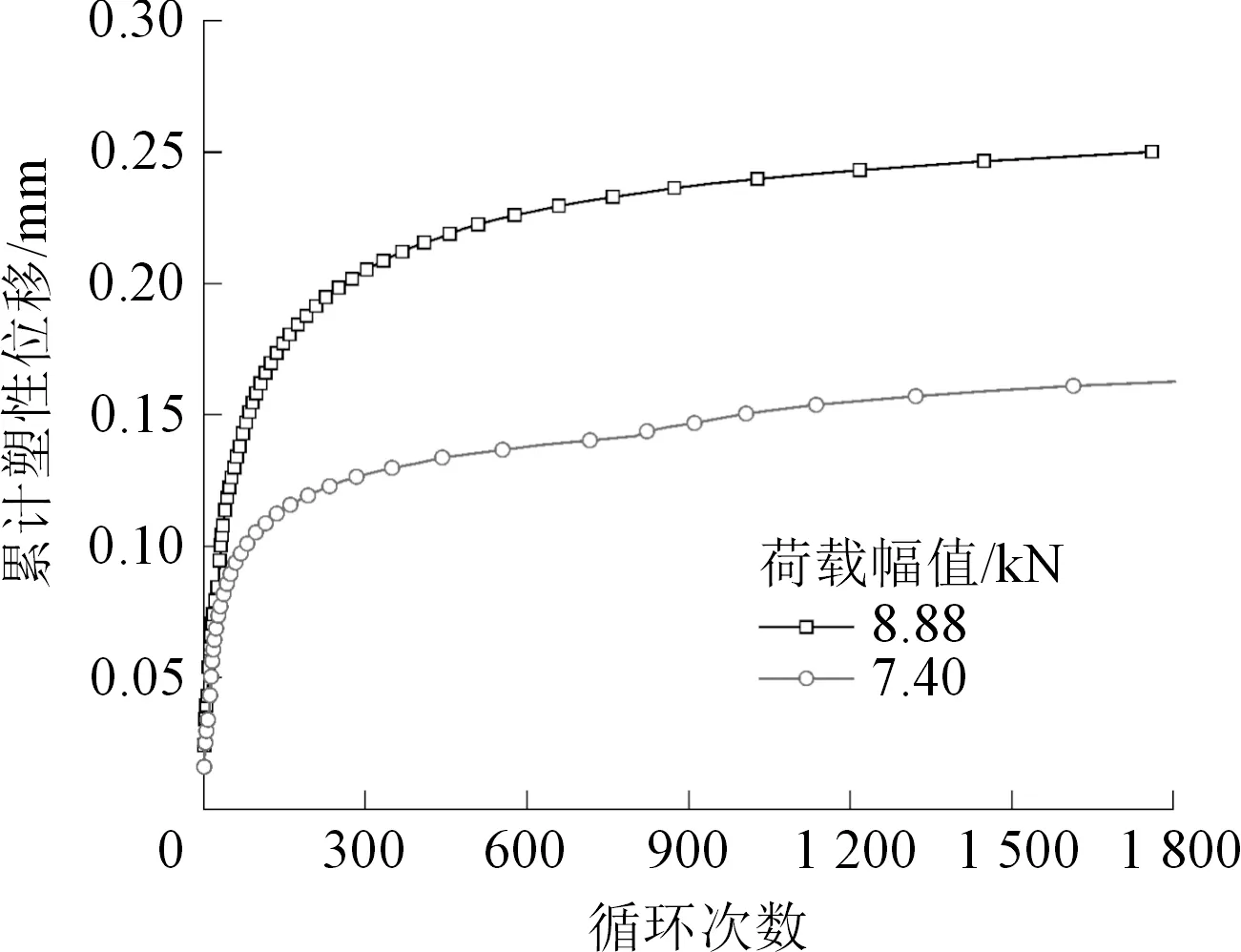
图12 不同荷载幅值累计塑性变形随循环次数变化Fig.12 Variation of cumulative plastic displacement with the number of cycles under different load amplitudes
4.3.3 阻尼比变化规律
岩石阻尼比是衡量岩石因外界激励而振动时能量耗散能力的重要参数,其数值大小反映了动态荷载作用下岩石因阻尼作用引起的能量耗散的多少。本文通过大理岩球砾的力-位移滞回曲线来计算阻尼比[19],进而研究动态循环加卸载时球砾的能量耗散特性。以上限荷载10.36 kN、振幅7.40 kN、频率1.00 Hz加载条件下大理岩球砾的阻尼比、能量随循环次数的变化关系为例来说明阻尼比的变化规律,如图13所示。由图13可见,第1次循环的塑性变形能和阻尼比均远大于后续循环,在前10次循环中,球砾的总变形能、塑性变形耗能随循环次数增加快速减小,而弹性变形能只是略有降低,因此导致阻尼比随循环次数增加显著减小。随后随荷载循环次数的增加,球砾的总变形能、塑性变形耗能、弹性变性能及阻尼比均呈现缓慢降低或减小的趋势。经过300次循环后大理岩球砾的塑性变形达到稳定值,每次循环产生的塑性变形很小,球砾的变形以黏弹性变形为主,阻尼比不再发生较大变化,稳定在5.23%左右。
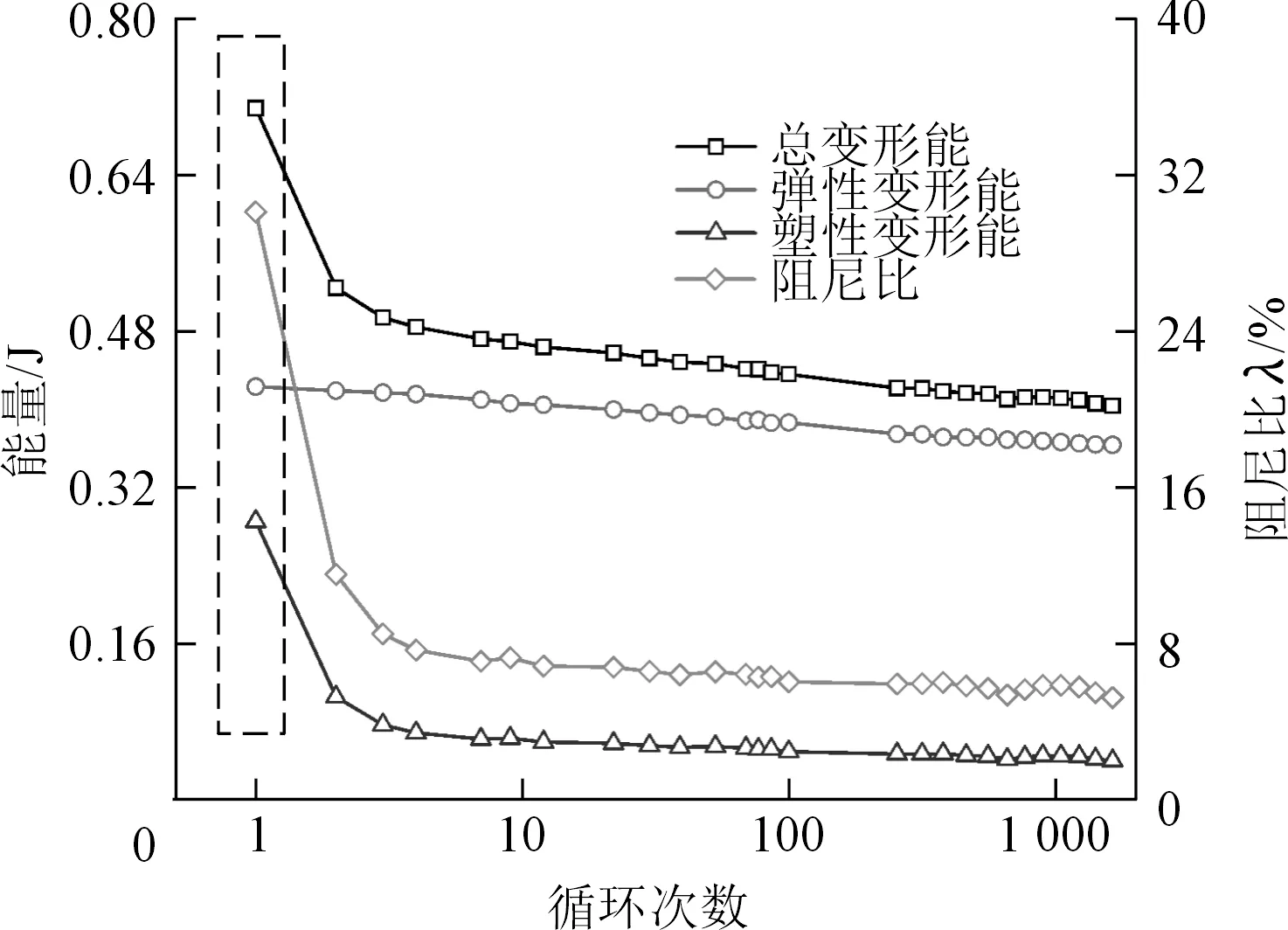
图13 大理岩球砾阻尼比、变形能随循环次数的变化关系Fig.13 Relation of damping ratio and deformation energy against the number of cycles
4.3.4 上限荷载和荷载幅值对阻尼比的影响
为研究动态循环加卸载试验中上限荷载对大理岩球砾阻尼比的影响,分别计算不同上限荷载加载条件下第3次、100次、1 000次循环球砾的阻尼比,得到上限荷载对大理岩球砾阻尼比的影响曲线,如图14(a)所示。可见阻尼比随上限荷载的增大而增大,尤其是试验初期,这种趋势最明显,如图14(a)中第3次循环的阻尼比,随上限荷载增大,阻尼比快速增大。经过试验初期的快速增长后,阻尼比开始相对稳定,随上限荷载的增大而变化很小,如图14(a)中循环第100次以及第1 000次时阻尼比变化趋势。上述现象说明提高上限荷载会导致大理岩球砾吸收更多的能量,从而提高球砾的损伤速率,减少球砾破碎所需的循环次数。
不同荷载幅值动态循环加卸载试验中,振幅为10.36 kN时大理岩球砾经过少数循环后就产生破碎。为更好地对比分析幅值对阻尼比的影响,分别计算第3次、10次和30次循环时球砾的阻尼比,得到荷载幅值对大理岩球砾阻尼比的影响曲线,如图14(b)所示。由图14(b)可见,荷载幅值对大理岩球砾阻尼比的影响与上限荷载的影响规律类似,即阻尼比随荷载幅值的增加而增大,尤其是试验初期,这种趋势也最明显,如图14(b)中第3次循环的阻尼比随荷载幅值增加而非线性增大,其特点是:当荷载幅值较小(<8.88 kN)时,阻尼比随荷载幅值增大而增长较慢;当荷载幅值较大(>8.88 kN)时,阻尼比随荷载幅值增大而增加较快。分析原因,是由于荷载振幅小时滞回环狭窄,耗散的能量较少,意味着每循环微裂纹的张开和闭合幅度小,阻尼比也就小;而荷载振幅较大时则滞回环面积也较大,每循环耗散的能量越多,阻尼比也就越大。随着荷载循环次数的增加,阻尼比随荷载幅值增大而增大的趋势变得平缓,如图14(b)中循环10次和循环30次时的结果,阻尼比只随上限荷载增加小幅度增长,甚至出现增长速率逐渐降低的趋势。
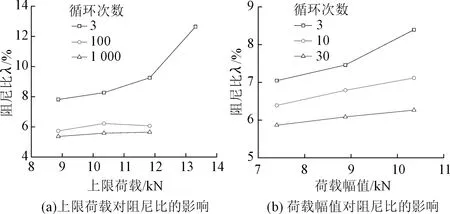
图14 上限荷载和荷载幅值对阻尼比的影响Fig.14 Effect of load amplitude and upper limit load on damping ratio
5 结 论
本文利用直径60 mm的大理岩球砾开展了一系列的压碎破碎试验、准静态循环加卸载试验和动态循环加卸载试验,分别研究了大理岩球砾在压缩荷载作用下的受力变形特征、累积塑性变形特征、阻尼比等,主要结论如下:
(1)大理岩球砾压缩破碎时屈服力约为破碎力的5.54%,屈服位移约为破碎位移的11.30%,说明大理岩球砾在受压过程中,弹性变形阶段较短,很快便进入弹塑性变形阶段。因此,在研究岩石颗粒变形问题时,不能简单采用Hertz弹性模型进行分析,而应重视对其塑性变形特征的分析。
(2)准静态加卸载试验中大理岩球砾表现出明显的循环硬化特征,即随加卸载次数增加,累计塑性位移、等效恢复系数和接触刚度-位移曲线的斜率都逐步增大,但增幅逐渐减小,最后趋近于稳定。第z次循环加载时的塑性变形曲线可以用模型spl,z=spl,1/zα较好地描述,其中α值随着上限荷载的增加而减小;前5次加卸载循环的等效恢复系数受上限荷载影响显著,随后逐渐减小,最终达到相同的稳定值;球砾的接触刚度随位移增加而增大,随循环次数增加这种趋势更加明显(接触刚度-位移曲线的斜率逐步增大)。
(3)动态循环加卸载试验中大理岩球砾塑性变形演化可以划分成3个阶段:初始阶段、等速阶段和加速(破坏)阶段。上限荷载和荷载幅值对大理岩球砾的塑性变形特征有较大影响,上限荷载越大、荷载幅值越大,大理岩球砾在初始阶段产生的塑性变形越大,累计塑性变形曲线进入等速阶段所需循环次数也越多。
(4)动荷载作用下阻尼比随循环次数增加而逐渐减小,最后渐趋于稳定。上限荷载越大、荷载幅值越大,大理岩球砾循环加卸载初期的阻尼比越大,随循环加卸载次数增加,上限荷载和荷载幅值对球砾阻尼比的影响逐渐减弱。
由于试验条件的限制,本文所开展的大理岩球砾室内压缩试验与堆石颗粒的实际受载仍存在较大差异,实际工程中接触模式是颗粒与颗粒之间的挤压接触,并且岩石颗粒往往受到周围多个接触颗粒的约束限制。在本文研究成果的基础上,侧向约束对大理岩球砾在循环加卸载条件下的接触力学特性的影响将是接下来研究工作的重点。

