基于双向预测插值的多维矢量鬼成像视频

刘 跃， 桑爱军， 宋立军， 王世刚

(1. 吉林大学 通信工程学院， 吉林 长春 130022； 2. 吉林工业职业技术学院， 吉林省 吉林市 132013)

计算鬼成像是一种可以在极端环境中成像的方法[1-3]，和传统的光学成像相比，计算鬼成像在方式上的独特之处在于，通过单像素探测器得到桶探测值(光强值)和对应的基图样并进行关联运算，重构出目标物体的图像.在性能上，这种成像方法对光的种类要求低，在可见光波段和不可见光波段都可以实现成像；在成本上，由于对光的空间分辨能力要求低，只需要一个单像素探测器，因此在特定的情况下也可节约成本.这种成像方法在最近的20年有了更进一步的发展，随着单像素相机的问世，2008年Shapiro介绍了空间光调制器和计算鬼成像两种新的鬼成像结构[4]，大大促进了鬼成像的发展速度；文献[5-7]进一步证明了使用热辐射的经典光束用于鬼成像方案的可能性；后来Walsh变换和Hadamard变换应用于鬼成像有效地提高了成像质量[8].经过不断地发展，深度学习的鬼成像[9]进展显著，在确定目标位置[10]方面的应用越来越广泛，鬼成像进一步应用于移动物体的成像也取得了很好的效果[11-14].

综上所述，可以看出运动物体的鬼成像的研究热度越来越高，但成像质量和成像速度等方面还存在问题，因此本文算法通过在基图样总数固定的情况下，把基图样均分成更少的组和目标物体相互作用，得到更清晰的几帧图像，再充分挖掘图像之间的相关性，得到了效果更佳的实时鬼成像视频.

1 理 论

1.1 多维矢量矩阵

假如H上的L1×L2数据排列(hl1l2)L1×L2命名为二维矩阵，记为HL1×L2，由此引出多维矩阵的定义，即H上的L1×L2×…×Ln数据排列为(hl1l2…ln)L1×L2×…×Ln，称为多维矩阵，记为HL1×L2×…×Ln.再将多维矩阵HL1×L2×…×Ln的维数分成两组，可以表示成H(Z1×Z2×…×Zm)×(X1×X2×…×Xv)，记为HZX，其中Z，X为矢量，Z=(Z1，Z2，…，Zm)，X=(X1，X2，…，Xv)，则称多维矩阵H是以维数按照矢量Z，X划分的多维矢量矩阵，又可简称为多维矢量矩阵[15].

多维矢量乘法：设EIL为I×L矩阵，FLJ为L×J矩阵，E=ei1…iml1…lk，F=fl1…lkj1…jn，则多维矢量矩阵E和多维矢量F相乘可得到一个I×J的矩阵D，D=di1…imj1…jn，乘积公式为

(1)

为说明方便，式(1)可简写为D=EF.

多维矢量矩阵的乘法规则和注意事项(设Q，T，K为多维矢量矩阵，x为常数)：

1) 交换律:在绝大多数情况下不满足交换律，即QT≠TQ.若Q，T为同阶方阵，在特定条件下有QT=TQ，则称Q，T为可交换矩阵.

2) 消去律:不满足消去律，如果QT=KT，不能得到Q=K.

3) 结合律:满足结合律，即Q(TK)=(QT)K.

4) 在多维矢量矩阵乘法中，零矩阵可以由两个非零矩阵的乘积得到.

5) 如果在式(2)中的乘法运算均可执行，则矩阵乘法可满足如下运算定律：

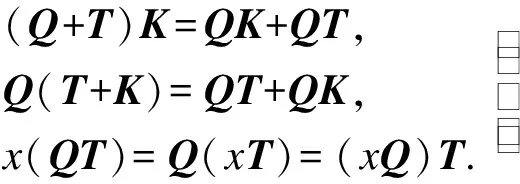
(2)

1.2 Walsh变换

Walsh变换是常见的正交完备变换，只包含+1和-1，所以生成简便.一维Walsh变换核函数可表示为

(3)

其中：N为Walsh变换的阶数，N=2n；u=0，1，2，…，N-1；x=0，1，2，…，N-1；gi(x)为x用格雷码表示的第i位；bi(x)为将x表示成二进制数的第i位.用式(3)可以生成形如(1，-1，…，1)T的一维矩阵，由变换核函数可得到一维Walsh变换公式，如式(4)所示：

(4)

其中，f(x)为二维目标物体的一维函数表示，同理二维Walsh变换可表示为

(5)

其中：W1=WN(x，y，u，v)是二维变换核函数；f(x，y)表示目标物体.

1.3 四维矢量Walsh变换

由多维矢量矩阵的定义和一维、二维Walsh变换原理可以得到四维矢量Walsh变换[16]，其变换核函数可由式(6)表示：

(6)

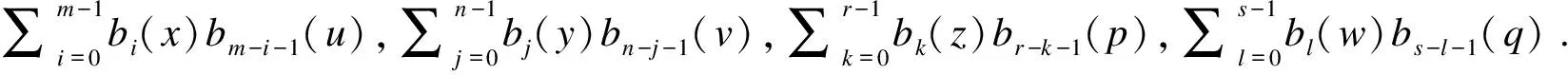
(7)

式中：W(N×N)×(N×N)为四维Walsh矢量变换核矩阵；f(N×N)×1和F(N×N)×1是二维矩阵的多维表示形式.

2 双向预测插值的多维矢量算法

2.1 四维矢量Walsh变换的实际应用

B(N×N)×1=W(N×N)×(N×N)O(N×N)×1，

(8)

(9)

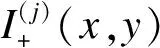
(10)

(11)

(12)

2.2 四维矢量Walsh变换能量集中特性

由于四维矢量Walsh变换鬼成像其实是将基图样和目标物体相互作用的过程等价地看成对目标物体进行正交变换，所以桶探测值可以看成是变换结果，通常用矩阵来表示，即变换系数矩阵.携带图像的有用信息越多表现为系数值越大，能量越高，从图1b可以看出，数值大的系数集中在相对靠左的方向上，即一维Walsh变换具有一定的能量集中特性，而从图1c可以看出数值大的系数集中在左上区域，由此可以清楚地说明四维矢量Walsh变换比一维Walsh变换的能量集中特性更好，并且其能量聚集在左上角.又因为Zigzag扫描[17]的顺序是从左上角成“之”字形到右下角的，可以充分利用四维矢量Walsh变换的能量集中特性，即用Zigzag扫描方法对数值大的系数(桶探测值)相对应的基图样进行排序，在实时采样时，重构品质可以得到很好的保障.

图1 变换系数矩阵

2.3 双向预测算法和块匹配算法

双向预测算法常用于图像编码，块匹配算法在图像处理中也有广泛应用，本文根据重构出的隔帧图像之间的时间和空间上的相关性以及物体的运动特点将这两种算法结合使用.由于双线性插值算法可以充分利用原图中的4个真实存在的像素值来共同决定目标图中的一个像素值，从而更真实地反映了原始图像的信息.首先对图像进行双线性插值，之后用块匹配算法采取全搜索的方式，精确地找出实时重构出的高质量隔帧图像间的运动矢量，再运用双向预测重构出中间帧，为了说明问题以图2为例.

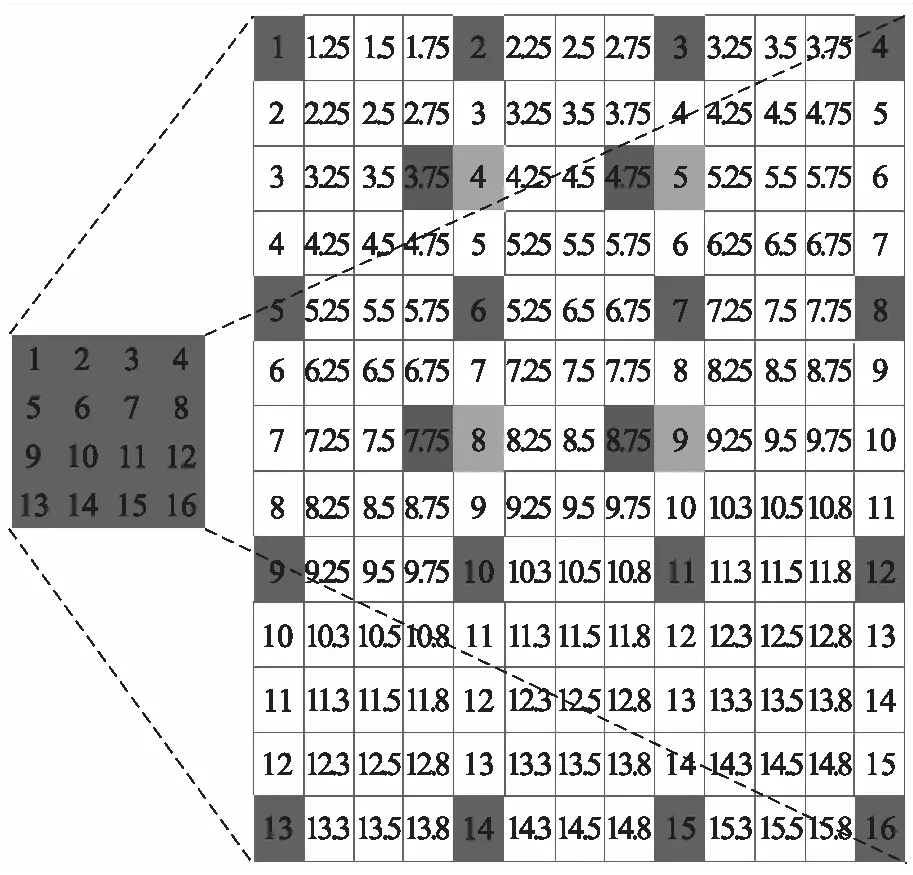
图2 图像空间插值和寻找运动矢量例图

在图2中，假设一帧图像的大小为4×4，像素值为1至16，利用块匹配算法在此帧中找到对应于相邻帧中某个固定的大小为2×2的块，如果此帧中像素值为6，7，10，11的像素块为最佳匹配块，这一过程找到的运动矢量精度为1个像素；再利用图像插值算法对此帧图像进行空间线性插值，找到像素值为6，7，10，11的像素块的周围8组2×2像素块分别与相邻帧中固定的块再次进行匹配，找到运动矢量，这一过程运动矢量精度达到1/2像素；再进行一轮这样的操作可将运动矢量精度精确到1/4像素.如果在第一轮操作中找到的运动矢量为(2，2)，在第二轮中像素值为4，5，8，9的像素块为最佳匹配块，则运动矢量为(1.5，2)，第三轮中像素值为3.75，4.75，7.75，8.75的像素块为最佳匹配块，则运动矢量为(1.5，1.75)，得到这个精确度达到1/4像素的运动矢量.再通过插值得到中间帧的过程用式(13)表示，双向预测示意图如图3所示.

(13)

其中：P(x，y)为根据时间相关性经过双向预测插值得到的图像；Pi，Pi+1表示相邻两帧，在本文中Pi和Pi+1分别表示用翻倍的基图样作用于目标物体得到的相邻两个隔帧图像；vx，vy为运动矢量的分量.

图3 双向预测示意图

2.4 算法的详细步骤

基于双向预测插值算法的多维矢量算法详细流程如图4所示.

步骤1 通过四维矢量Walsh矩阵和式(10)得到全正基图样，经过Zigzag排序后作用于目标物体，得到隔帧图像；

步骤2 将得到的隔帧图像用双线性插值算法进行空间插值，通过块匹配算法得到1/2像素精度的运动矢量，再通过块匹配算法得到1/4像素精度的运动矢量；

步骤3 根据得到的高精度的运动矢量通过双向预测算法进行时间插值，得到实时图像.

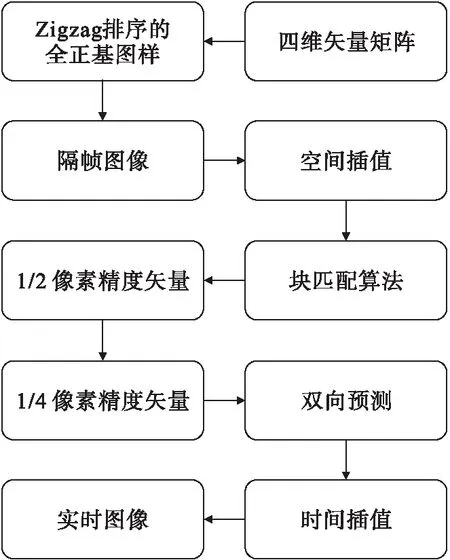
图4 算法流程图

3 算法分析

3.1 实验结果

本文选用NRSS评价方法来评估实验结果.NRSS是一种在没有参考图像的情况下，根据人的主观感受，以图像清晰度来评价图像品质的方法[18]，数值越小表示成像品质越好，图像清晰度用VNRSS表示.

(14)

其中，SSIM(xi，yi)代表结构相似度.

图5为用全正基图样在采样数为1 760的条件下，通过对目标物体的桶探测值进行四维矢量Walsh逆变换，重构得到13帧隔帧图像实验结果，简述为全正基图样隔帧实验结果.图6为用正负交替基图样在采样数为1 760的条件下，通过对目标物体的桶探测值进行四维矢量Walsh逆变换，重构得到13帧隔帧图像实验结果，简述为正负交替基图样隔帧实验结果.图7为用全正基图样在采样数为1 760的条件下，通过对目标物体的桶探测值进行四维矢量Walsh逆变换，重构到13帧图像，再经过双向预测插值得到的25帧图像的实验结果，即本文算法，简述为全正基图样预测插值法的实验结果.图8为用全正基图样在采样数为880的条件下，通过对目标物体的桶探测值进行四维矢量Walsh逆变换，直接重构得到25帧图像的实验结果，简述为全正基图样直接成像法的实验结果.图9为用正负交替的基图样在采样数为1 760的条件下，通过对目标物体的桶探测值进行四维矢量Walsh逆变换，重构出的13帧图像经过双向预测插值得到25帧图像的实验结果，简述为正负交替基图样预测插值法的实验结果.

图5 全正基图样隔帧实验结果

图6 正负交替基图样隔帧实验结果

图7 全正基图样预测插值法(本文算法)的实验结果

图8 全正基图样直接成像法的实验结果

图9 正负交替基图样预测插值法的实验结果

图10为全正基图样预测插值法和全正基图样直接成像法两者之间图像清晰度VNRSS对比曲线，图11为全正基图样预测插值法和正负交替基图样预测插值法两者之间的图像清晰度VNRSS对比曲线，即在图10和图11中，比较了基于双向预测插值的多维矢量鬼成像视频算法和其他算法的VNRSS值的大小.

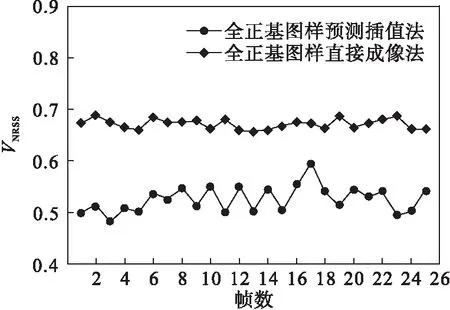
图10 全正基图样预测插值法和全正基图样直接成像法的图像清晰度VNRSS对比

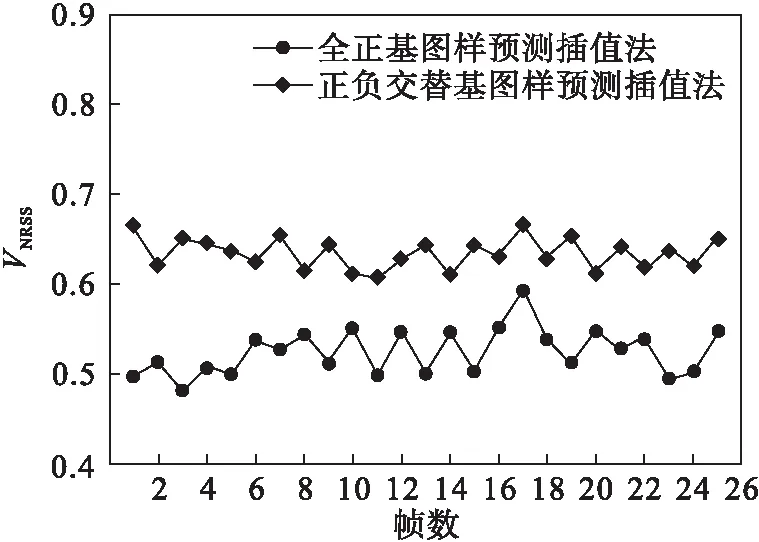
图11 全正基图样预测插值法和正负交替基图样预测插值法的图像清晰度VNRSS对比

3.2 性能分析

由图5和图8相互比较可以直观地看出，用全正基图样在采样数为1 760的条件下，对目标物体桶探测值进行基于四维矢量Walsh逆变换，重构得到的图像明显比用全正基图样在采样数为880的条件下，对目标物体桶探测值进行基于四维矢量Walsh逆变换，直接重构得到的图像更清晰.由图10可知全正基图样预测插值法的实验结果的VNRSS分布在0.50～0.60之间，用全正基图样直接成像法得到的实验结果对应的VNRSS在0.65～0.70之间，由图11可得用正负交替基图样预测插值法得到的实验结果对应VNRSS在0.60～0.70之间.由图10和图11可以看出，运用本文算法得到的数据曲线都位于用其他算法得到的数据曲线的下方，根据NRSS评价标准，所得实验结果支持基于双向预测插值的多维矢量鬼成像视频算法好于全正基图样直接成像算法.又由图11和表1可以得出，在实时状态下，由于本文算法选取的全正基图样的有效性高于需要差分操作的正负交替基图样，因此基于双向预测插值的多维矢量鬼成像视频算法也同样优于正负交替基图样的预测插值算法.

表1 各种算法的NRSS评价方法的图像清晰度比较

本文算法相较于现行大多数移动物体鬼成像算法最大的创新是将总数一定的有效正基图样少分组，从而更加集中地作用于目标物体,得到数量稍有减少但质量更高的重构图像，再根据重构图像相邻帧之间的时空强相关性，用块匹配和双向预测插值算法得到运动物体的全部重构图像.因为块匹配和双向预测插值的应用可以大大缩短重构中间帧的时间，从而使本文算法要比总数一定直接均分基图样作用于目标物体和大量增加基图样数量再均分作用于目标物体的两大类现行移动物体鬼成像重构算法，更快速、更简便、更清楚得到物体的实时图像，更加适合在深海、太空、云雾等光源较差的复杂环境下对移动物体快速高质量成像.

4 结 语

本文提出了基于双向预测插值的多维鬼成像视频算法，该算法根据视频中前后两帧图像之间的时间和空间相关性，用总数固定的基图样重构出数量较少但质量更高的隔帧图像，通过空间插值，用块匹配算法找到精确到1/4像素精度甚至精度更高的运动矢量，再通过双向预测进行时间插值，得到隔帧图像的中间帧，在实时状态下得到很好的成像效果，这是一种比直接均分基图样对目标物体进行重构的成像方法更高效的实时视频成像算法.