一种微位移柔顺放大机构的优化设计

郭凡逸， 孙志礼， 张胜男， 曹汝男

(东北大学 机械工程与自动化学院， 辽宁 沈阳 110819)

与传统的刚性机构相比，柔顺机构具有体积小、质量轻、无装配误差、运动过程中无摩擦、无侧隙等优点.因此，柔顺机构在医疗[1]、精密仪器[2]、快速伺服装置[3]等许多应用中得到了广泛的应用.柔顺机构由刚性模块和柔顺模块串联和并联组成.为了实现大范围的运动，位移放大器是柔顺机构中不可或缺的重要部分.

许多柔顺机构使用杠杆进行位移的传递与放大[4].一些机构采用多级杠杆的形式来增加放大率[5]，但这样会增加机构本身的复杂性.桥式机构是一种结构简单的位移放大器[6-7].它具有紧凑的结构以及高放大倍数，但是这种结构也存在一些缺陷.集中质量的存在将大大降低桥式机构的动态性能.菱形机构作为一种特殊的桥式机构，避免了集中质量的问题[8].但无论机构的约束条件是否改变，压电陶瓷驱动器会随着机构运动的现象仍然存在.与桥式机构相比，Scott-Russell机构也存在类似的问题[9-10],这种位移放大机构仍然具有集中质量，从而导致较低的固有频率.本文的微位移柔顺放大机构是一种无集中质量的全柔顺位移放大器[11]，在实现位移放大功能的同时又具有良好的动态特性.

此外，关于柔顺机构的优化也是研究的热点问题.文献[12]基于模糊逻辑的田口方法对位移放大比和一阶固有频率进行了优化.该方法弥补了田口法只能用于单目标优化的缺点，具有较快的收敛速度.遗传算法也用于解决结构优化问题[13]，该方法虽然可以直接搜索最优参数，但求解时间较长.文献[14-15]还提出了两种基于响应面法的优化算法.该方法通过多项式拟合得到近似目标函数，即求解多项式系数的过程.如果目标函数的非线性程度较高，拟合出的响应面会存在一些误差，同时设计参数过多，也会增加响应面拟合的困难.本文基于柔性梁的伪静态模型建立了一种微位移柔顺放大机构参数化模型，并且得到了目标函数的解析式.该解析模型包含了微位移柔顺放大机构的所有尺寸参数，通过模拟退火算法可以快速优化其尺寸和形状.同时考虑了负载与加工误差因素，分析了输出端存在负载时机构在不同输入位移下的放大率变化规律以及机构关键节点处的加工误差对输出位移的影响.

1 柔性梁的动刚度矩阵

微位移柔顺放大机构由一些柔性梁组合而成，将每根柔性梁当作一个单元，则第i个柔性梁单元在局部坐标系下的受力与几何尺寸如图1所示.

图1 柔性梁单元的受力与几何尺寸

柔性梁单元有j，k两个节点，每个节点有沿着x，y方向移动和绕着z方向转动3个方向自由度.局部坐标系下刚度矩阵为

(1)

对矩阵中的每个元素应用泰勒级数展开：

(2)

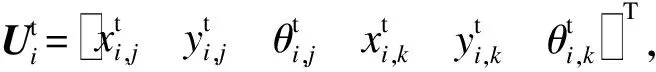
那么节点力与位移的关系为

Fi=KiUi.

(3)

将梁两端局部坐标系下的力与位移分别转化为参考坐标系中的力和位移，则式(3)变为

(4)

(5)

(6)

其中：Ri是坐标旋转矩阵；Pi是坐标平移矩阵.则第i个梁单元在参考坐标系下的刚度矩阵为

(7)

将式(7)代入式(4)并将其改写成分块矩阵的形式：

(8)

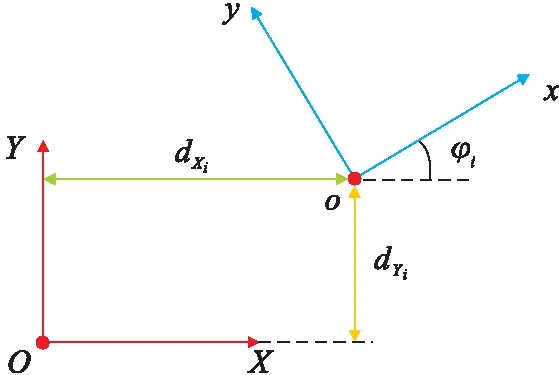
图2 局部坐标系与参考坐标系

2 微位移柔顺放大机构的伪静态模型

位移放大机构的模型如图3所示，其工作原理是在输入端输入微小位移，通过组合柔性梁的变形在输出端输出放大后的位移.输入、输出位移都是沿着Y方向的，而X方向位移与Z方向的转动都是不需要的.因此将其设计成轴对称形状，从而消除输出端的不必要的位移.

图3 微位移柔顺放大机构

在进行静/动态分析时，首先要将模型离散化.在本文中，将位移放大器离散成10根柔性梁，整个模型共有8个节点，由于节点I与A最后都等效到节点O(参考坐标系原点)上.机构的受力分析如图4所示.对于任意节点，其所受的合外力等于与其相连的梁施加在其上的力，依据此关系，列出整个模型的方程：

O节点模型方程为

(9)

B节点模型方程为

(10)

D节点模型方程为

(11)

E节点模型方程为

(12)

F节点模型方程为

(13)

H节点模型方程为

(14)

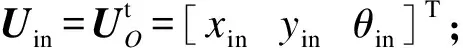
将方程(9)～(14)写成矩阵的形式为

(15)

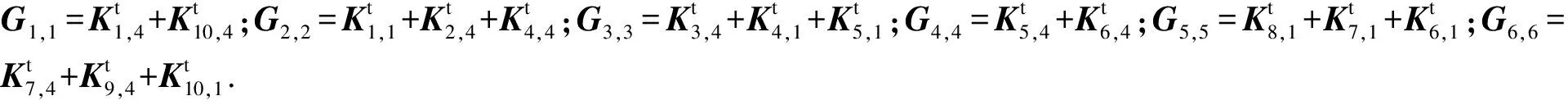
放大率Ar为

Ar=yout/yin.

(16)

3 结构优化

本文主要通过调整柔性梁的宽度与厚度来优化机构的放大率.优化过程中改变其中某一柔性梁的尺寸参数，则与其对称的柔性梁的尺寸参数也随之改变，那么只需要优化一半的模型，提高了计算效率，同时优化后的模型仍然是严格对称的.

图4 微位移柔顺放大机构受力分析

机构原始构型尺寸参数如表1所示，假设材料各处的弹性模量都相同，E=71 GPa，密度ρ=2 810 kg/m3，泊松比μ=0.33，所有柔性梁的截面尺寸也都相同，ti=0.5 mm，wi=10 mm.在输入端(节点O)输入一定的力或位移，通过该柔顺位移放大机构，从输出端(节点E)输出放大后的位移.本机构只放大Y方向的位移，X与Z方向的位移是不需要的，因此在输入端只有输入位移yin.

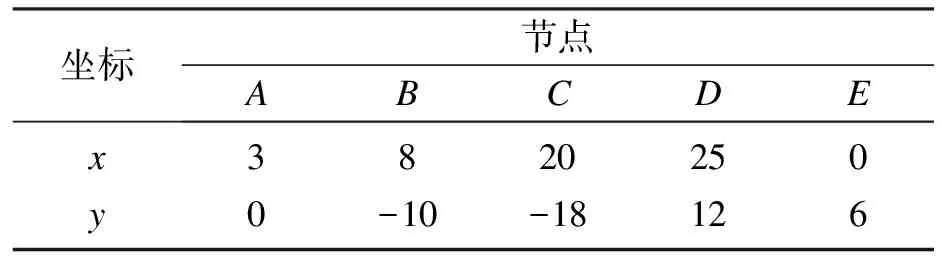
表1 微位移放大机构各节点坐标

各柔性梁的宽度wi变化是5.0～15.0 mm，无负载(Fout=0)时， 各柔性梁宽度对机构放大率的影响如图5所示.从图中可看出，只有w5与放大率的关系是相反的，且其对放大率的影响也是最显著的，其余参数与放大率都呈正向的关系；w1与w2对放大率的影响几乎一致；w3与w4的曲线比较平稳，它们的变化几乎对放大率没有影响.

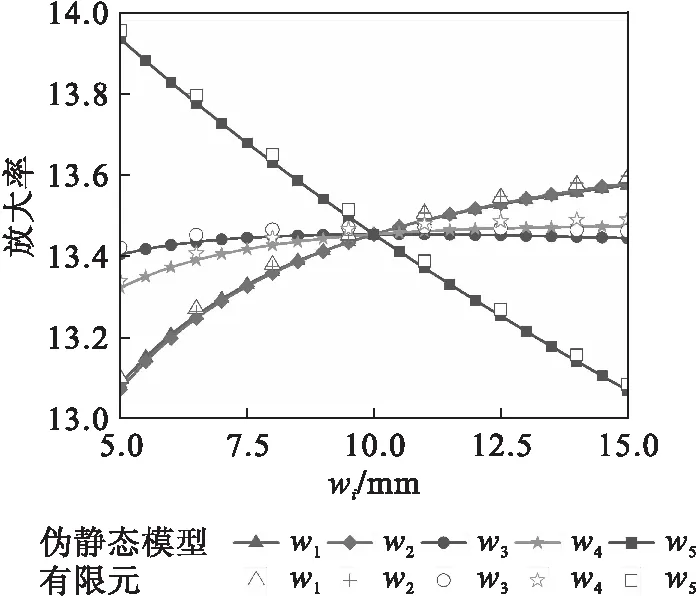
图5 各柔性梁单元宽度对放大率的影响

各柔性梁的厚度ti变化是0.3～1.0 mm，无负载(Fout=0)时，各柔性梁厚度对机构放大率的影响如图6所示，图6b为图6a的局部放大图.由图可知，t5对放大率的影响是最显著的；t1与t2对放大率的影响几乎一致，t3与t4对放大率的影响也基本相同，放大率对这4个参数均不敏感.

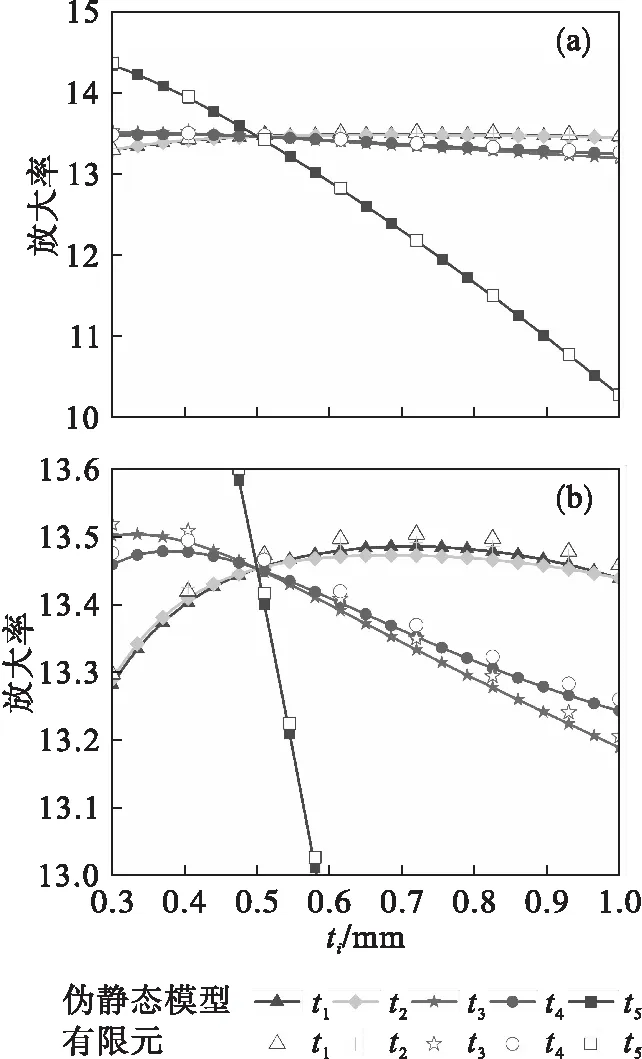
图6 各柔性梁单元厚度对放大率的影响

优化后，各柔性梁单元尺寸如表2所示.

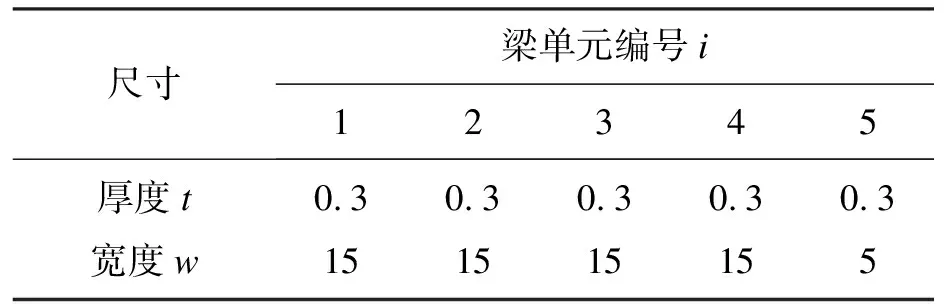
表2 柔性梁单元尺寸

优化后的模型与原始模型输出位移对比如图7所示.优化后机构的输出位移与原始模型相比有了明显的提高.可以看出随着输入位移的增加，有限元仿真的结果与理论结果差距越来越大，这是由于伪静态模型忽略了梁变形时产生的应力刚化效应.但是在输入位移较小时，梁的变形也较小，这种应力刚化效应并不显著，所以理论模型仍然是准确的.

图7 优化模型与原始模型输出位移对比

当输入位移xin=10 μm与负载Fout=0时，原始模型与优化模型的位移放大率如表3所示.

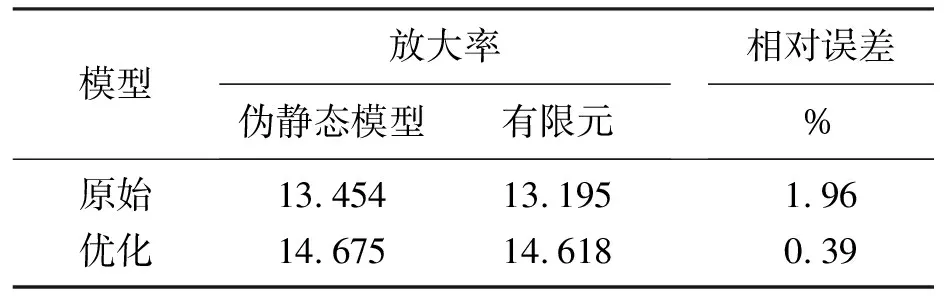
表3 优化模型与原始模型放大率对比

放大率随负载的变化如图8所示.负载与放大率呈线性负相关关系，而且当输入位移越小，这种负相关越明显.随着输出位移的增加，负载对放大率的影响逐渐减小.

图8 放大率与负载的关系

4 加工误差对输出位移的影响

当节点坐标存在加工误差时，柔顺位移放大机构也将不再完全对称，输出端将产生两个额外方向的位移xout与θout.假设节点D的加工误差为ΔxD与ΔyD，节点F的加工误差为ΔxF与ΔyF，那么相应的节点D与节点F的坐标为(xD+ΔxD，yD+ΔyD)与(xF+ΔxF，yF+ΔyF)，假设ΔxD=ΔxF且ΔyD=ΔyF，那么由于结构的对称关系，节点D与节点F的加工误差对输出位移的影响程度是完全一致的，因此只需要研究一半的模型加工误差对输出位移的影响.为了研究不同节点的加工误差对输出位移影响程度，故将各节点在X与Y方向的加工误差限制在±50 μm.

假设节点j的原始坐标为(xj，yj)，当节点j存在加工误差Δxj与Δyj，那么节点j的坐标表示为

(17)

相应地，柔性梁单元的几何参数也会发生改变，表4表示加工误差存在时，各柔性梁单元的几何参数变化.

表4 梁单元几何参数

当输入位移yin=10 μm且负载为0时，优化模型的节点A，B，C，D，E的加工误差对输出位移的影响如图9所示.实线代表xout，虚线代表θout.首先，加工误差与输出位移近似呈线性关系，且误差的增大必然导致输出位移的增大，但方向不同.当直线斜率为正时，表明X方向上误差增加的方向与输出位移增加的方向一致；当直线的斜率为负时，表示X方向上误差增加的方向与输出位移增加的方向相反.当三角形点在顶部时，说明Y方向上的加工误差的增加方向与输出位移的增加方向一致.当正方形点在顶部时，表示Y方向上的加工误差的增加方向与输出位移的增加方向相反.在图9e中三条线是堆叠在一起的，这说明无论ΔyE如何变化，都不会产生xout与θout. 这是由于ΔyE的变化并不会影响结构的对称性.值得注意的是，直线的斜率大小并不能作为对于加工误差影响程度的判据，因为各坐标轴的单位不同.由图可知，ΔxE对θout的影响是最大的；ΔxD对xout的影响最大.

图9 加工误差与输出位移的关系

5 固有频率

柔顺放大机构的整体动态刚度矩阵G如式(15)所示，通过求解矩阵行列式得到结构的固有频率：

det(G)=0

(18)

优化模型的前三阶固有频率如表5所示.通过比较结果可以看出，这种伪静态模型可以准确地预测模型的固有频率，且相对误差小于1%.前三阶固有频率所对应的振型如图10所示.由于本位移放大机构的运动方向是沿着Y轴的，所以1阶与3阶固有频率为主运动方向的频率，也是可能产生共振的频率.而2阶振型是沿着x轴振动，因此在沿着Y轴的激励下，该振型并不会被激发.

表5 优化模型的固有频率

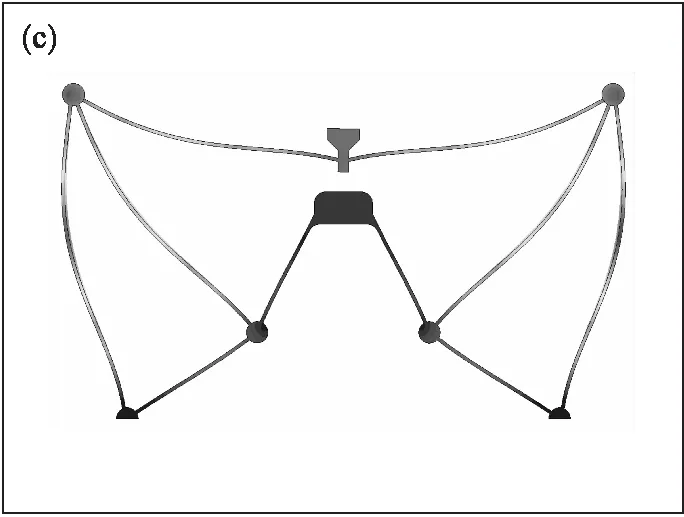
图11 优化模型的振型

6 结 论

1) 基于动刚度矩阵与矩阵位移法建立了微位移柔顺放大机构的伪静态参数化模型，同时也得到了放大率的解析式.以放大率为目标，通过模拟退火算法优化柔性梁的厚度与宽度，得到了一种新的机构，这种机构的放大率相比原始构型提高了9%，同时这种机构的固有频率达到了409 Hz.

2) 随着负载的增加，机构的放大率逐渐降低；当输入位移增加时，负载对机构放大率的影响减弱.节点的加工误差使机构的输出端产生额外两个方向的位移，且机构的顶点与输出端的X方向加工误差对输出位移的影响最大.