圆柱直齿轮铣削加工无干涉刀具路径规划

王振宇， 张荣闯， 于天彪

(1.东北大学 机械工程与自动化学院， 辽宁 沈阳 110819； 2.东北大学秦皇岛分校 控制工程学院， 河北 秦皇岛 066004)

随着数控技术的发展，通用铣刀多轴加工，因其在齿轮加工过程中具有的高度柔性化，已成为一种重要的齿轮加工方法[1-4]. 相对于传统的滚齿等加工方法，铣削加工在新式齿轮的快速原型制造、大型齿轮的单件生产以及齿轮的修复等方面具有明显的优势. 由于采用多轴铣削加工，合理地规划刀具路径是保证齿轮加工精度和加工效率的关键.

齿轮铣削刀具路径规划主要有以下两种方法.一是渐开线包络法. 齿轮齿廓既可通过立铣刀的侧刃，类似于滚刀直线刃包络出渐开线，也可以通过球头铣刀圆弧刃包络出渐开线，两种方式在工业中都有广泛应用. Özel 采用径向铣齿加工齿轮，根据渐开线方程推导出切削路径和齿廓偏差，分析加工参数和齿轮参数对二者的影响[5-6]. Guo 等提出一种渐开线圆柱齿轮立铣刀包络铣削加工方法，通过所建立的数学模型分析齿面精度和刀具路径之间的关系，实现铣刀具路径规划与齿面精度特性优化匹配[7].郭二廓等推导出立铣刀侧铣加工齿轮的齿廓误差模型，研究了刀具进给策略、齿轮几何参数对齿廓误差的影响[8]. Shi 等研究了粗糙度一致性约束下的圆柱齿轮铣削路径规划方法，通过渐开线的等距线确定出刀位点[9-10].二是自由曲面包络法.即将齿廓曲面拟合成自由曲面，根据自由曲面的多轴加工方法来铣削齿轮.Kawasaki 等将锥齿轮设计齿廓点导入到CAM软件中，进行光顺后形成NURBS曲面，进而利用CAM软件中自由曲面铣削功能实现齿廓铣削加工的刀具路径规划[11]. Bouquet等在CAD/CAM软件中对圆柱齿轮铣削进行刀具路径规划，将切削过程分为立铣刀齿坯加工、立铣刀齿槽粗加工、立铣刀齿面粗加工，以及保证齿廓精度的球头铣刀精加工四个步骤[1].lvarez 等基于CAM软件在多任务五轴机床大型螺旋锥齿轮铣削加工中制定不同的加工策略和刀具路径，通过误差分析优化刀具路径[12]. Staudt 等对圆柱齿轮自由铣削加工过程进行详细论述，包括CAX过程链确定、刀具选择以及加工策略选择等[3]. 相对于自由曲面包络法，渐开线包络法可以根据齿廓的几何特性、齿廓精度要求，准确地计算出刀具路径.上述研究成果中，刀具路径规划主要集中于刀位点的计算，算法较少涉及铣刀与齿廓之间的全局干涉以及刀具半径过大造成局部干涉问题的处理.

基于此，以球头铣刀圆弧刃铣削圆柱直齿轮保证齿廓精度的精加工为对象，利用渐开线包络法确定出铣刀圆弧刃包络齿廓的刀位点，通过干涉判断计算出无干涉条件下刀具偏角范围，提出一种无干涉圆柱齿轮球头铣削刀具路径规划方法，通过仿真实例验证该方法的可行性和有效性.

1 齿轮铣削加工数学模型

1.1 铣削运动模型

铣削运动如图1所示，采用四轴数控机床进行齿轮包络铣削加工，工件固定在B轴上，跟随B轴旋转实现间歇分度运动；球头铣刀固定在回转主轴S轴上，通过x，y，z轴直线进给定位，完成工件材料去除加工.

图1 齿轮铣削运动示意图

图2所示为齿轮铣削坐标系统. 机床坐标系oM-xMyMzM与机床床身固定连接，定义为坐标系统的绝对坐标系，zM轴与齿轮回转轴线重合；坐标系oW-xWyWzW与工件固定连接，坐标轴yW与齿廓中心线重合，围绕机床坐标系的zM轴作间歇回转分度运动，φ表示工件回转的角度；坐标系oT-xTyTzT为球头铣刀坐标系，坐标原点oT位于球头铣刀的球心，坐标轴zT与机床主轴轴线一致；oG-xGyGzG为描述轮齿齿廓数学模型的齿廓坐标系，其轴线yG与齿廓中心线重合；φ为与工件坐标系之间的夹角，当φ=0时，与工件坐标系相重合.

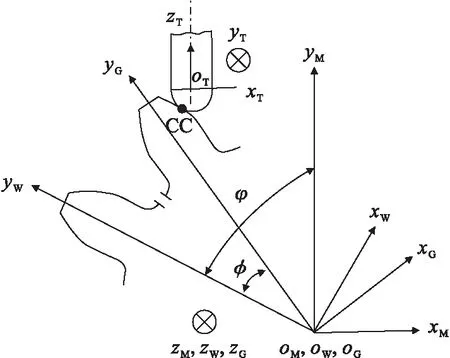
图2 齿轮铣削坐标系统

齿廓坐标系与工件坐标系之间的变换矩阵为

(1)

工件坐标系与机床坐标系之间的变换矩阵为

(2)

则齿廓坐标系与机床坐标系之间的变换矩阵为

MMG=MMWMWG.

(3)

1.2 齿廓几何模型

(4)

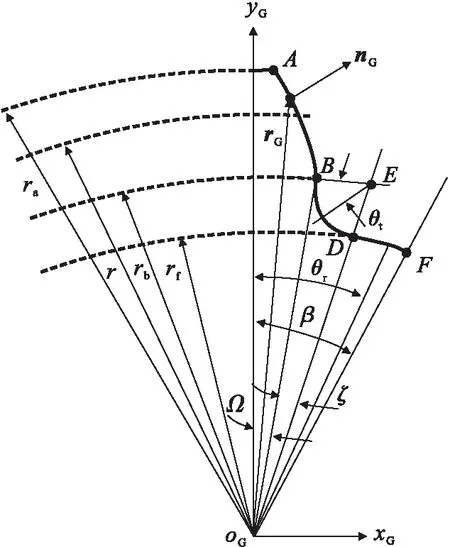
图3 直齿轮齿廓几何模型

(5)

(6)

(7)

式中，0≤θt≤π/2-ζ.

(8)

式中，Ω+ζ≤θr≤β，β=π/z.

(9)

(10)

(11)

2 齿轮铣削刀具路径规划

齿轮铣削刀具路径规划包括刀位点计算和刀轴矢量计算两部分.刀位点计算主要确定刀具在铣削过程中的刀具位置；刀轴矢量计算主要是确定无干涉条件下的刀具偏角范围.

2.1 刀位点计算

2.1.1 渐开线齿廓刀位点计算

渐开线齿廓刀位点的确定取决于齿廓铣削的刀具进给策略；进给策略主要有等残留高度、等弧长、等径向三种，等残留高度刀位点计算是其余进给策略刀位点计算的基础.

1) 等残留高度进给策略刀位点计算.

图4所示为渐开线齿廓刀位点计算示意图.理论齿廓曲线ε1是不同刀位点刀具圆弧的包络线；CG，K，LG，K分别为已知的刀触点和刀位点，对应的渐开线压力角为αK，LG，K+1为需要求取的刀位点.ε2为等残留高度曲线，ε3为刀具路径曲线；GK为等残留高度点，位于ε2上，到ε1的距离为残留高度h，同时也是相邻两个刀位点刀具圆弧的交点.

图4 渐开线齿廓刀位点计算

ε2表示为

rGh(α)=rG(α)+nG(α)h.

(12)

ε3表示为

rGR(α)=rG(α)+nG(α)R.

(13)

CG，K点和LG，K点的位置表示为

(14)

建立刀位点LG，K处的刀具圆弧坐标系oJ-xJyJ，原点oJ位于LG，K点，ε1的法向nG，K为yJ轴，切向为xJ轴，刀具圆弧可表示为

(15)

刀具圆弧在齿廓坐标系下可表示为

rG(αk，θ)=LG，K(αK)+rJ(θ).

(16)

由式(12)和式(16)，残留高度点GK表示为刀具圆弧rG(αk，θ)和ε2的交点，满足

rG(αk，θ)-rGh(α)=0.

(17)

式(17)采用数值计算的方法求解，其求解涉及到：

①rG(αk，θ)在ε2上的投影点；

② 求取θh，满足|rG(αk，θh)-rGh(α)|=0.

rG(αk，θ)在ε2上的投影点对应最短距离，定义距离平方函数为

f(α)=|rG(αk，θ)-rGh(α)|2.

(18)

通过Newton-Raphson迭代法求取rG(αk，θ)到ε2最小距离的投影点，迭代过程的初值为αk.

Newton-Raphson迭代法需要确定θ的初值，定义rG(αk，θ)到ε2的距离函数为

d(θ)=|rG(αk，θ)-rGh(α)|.

(19)

求取角度θh，满足d(θh)=0，本文采用二分法进行求取；采用刀触点CG，K对应的角度值，即θh=0作为迭代初值，沿着步距方向采用二分法进行搜索[15].

求出等残留高度点GK后，刀具路径上下一个刀位点LG，K+1通过下面几何关系进行求解：LG，K+1位于刀具路径曲线ε3上；GK点到LG，K+1点的距离由刀具半径R确定.LG，K+1点的具体计算方法与GK点求取类似.

2) 等弧长、等径向进给策略刀位点计算.

图5所示为等弧长和等径向进给示意图.图5a中ΔS为常量，图5b中Δy为常量，刀位点计算以等残留高度计算结果为基础.图6所示为等残留高度计算出的刀触点CG，K，CG，K+1之间的弧长ΔSK与径向间距ΔyK，计算公式如下：

(20)

式中，

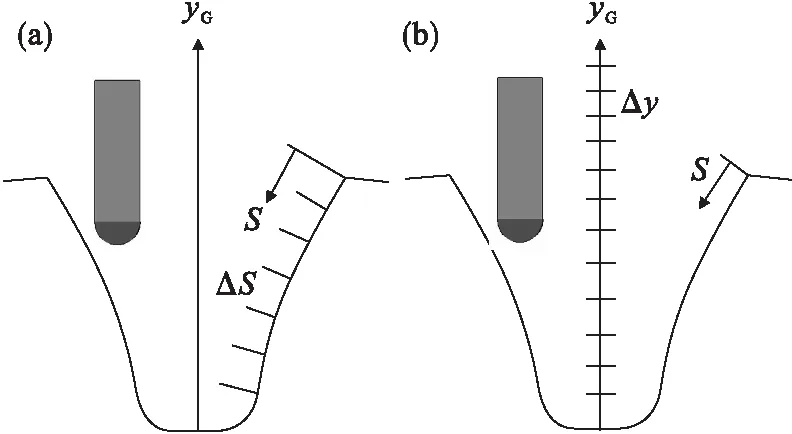
图5 等弧长、等径向进给策略

图6 ΔSK和ΔyK计算

保证齿廓精度，要求等弧长、等径向进给下的残留高度不能大于残留高度h，求出等残留高度下相邻刀位点中的ΔSmin,Δymin，计算公式如下：

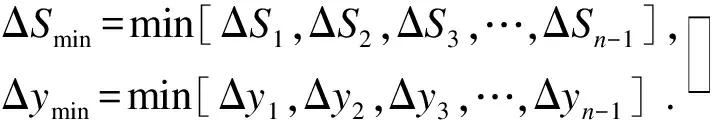
(21)

式中，n为渐开线齿廓刀位点数.

以ΔSmin为相邻刀位点计算的离散弧长，计算出LG，K+1点对应的等弧长进给下的压力角αK+1为

(22)

式中:SAB为渐开线弧长；αA为齿顶圆A点对应的压力角.

以Δymin为相邻刀位点在径向上进给的离散间距，通过数值计算得到LG，K+1点对应的压力角αK+1为

(23)

式中，yG，A为齿顶圆A点的纵坐标.

根据式(22)和式(23)求出αK+1之后，将其代入到式(14)，计算出对应的LG，K+1点的位置.

2.1.2 过渡曲线和齿根曲线刀位点计算

过渡齿廓和齿根齿廓均为圆弧曲线，本文中采用等残留高度进给策略进行铣削. 通过解析法进行求解. 如图7所示，过渡齿廓为凹圆弧，过渡圆弧的半径为rt=|rG，E-rG，B|，则相邻刀位点之间的间隔角δ1表示为

(24)

式中：l1=rt-R；l2=R；l3=rt-h.

LG，K+1点的位置表示为

LG，K+1(δ1)=M(δ1)(rG，B-rG，E)/|rG，B-rG，E|·l1.

(25)

如图8所示，齿根圆为凸圆弧，与过渡曲线刀位点计算相似，则δ2表示为

(26)

式中：l4=rf+R；l5=R；l6=rf+h.

LG，K+1点的位置表示为

LG，K+1(δ2)=M(δ2)rG，D/|rG，D|·l4.

(27)

图7 过渡曲线刀位点计算

图8 齿根圆刀位点计算

由图2可知，机床坐标系下的刀位点计算，应先确定工件回转角φ. 图9所示，定义齿廓法向量nW，K和刀轴矢量tW，λ之间的夹角λ为刀具偏角，相对于nW，K旋转逆时针为正，顺时针为负，其范围为[-π/2，π/2].

tW，λ表示为

tW，λ=MW，λnW，K.

(28)

主轴S矢量T=[0 0 1]，与tW，λ之间的夹角φ即为工件的回转角，计算公式为

φ=arctan(tWx，λ/tWy，λ).

(29)

图9 工件回转角φ

2.2 刀具偏角范围计算

刀具轴向矢量主要取决于刀具偏角的选择，刀具偏角主要通过刀具干涉判断来确定.

1)干涉类型.齿轮铣削过程中主要有两种干涉状况，分别为局部干涉和全局干涉.局部干涉通常指采用过大的刀具半径时导致齿根产生过切干涉，可以通过改变刀具半径大小来避免，如图10所示；全局干涉通常指刀具整体与工件的渐开线齿廓相碰撞，可以通过改变铣刀刀轴方向来避免，如图11所示.

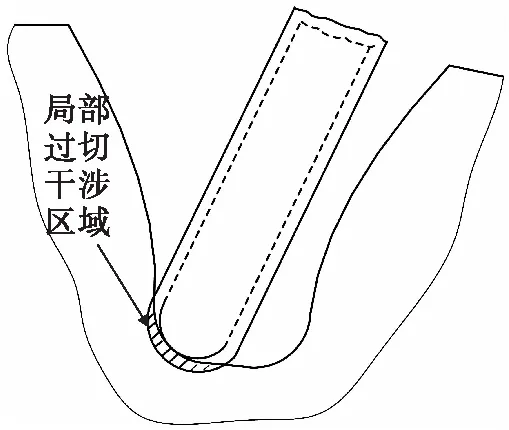
图10 局部过切干涉与避免

图11 全局干涉与避免

2)局部干涉产生和避免.齿轮齿廓中渐开线齿廓和齿根圆齿廓为凸面，不能够产生局部过切干涉；而过渡曲面为凹曲面容易产生局部过切干涉.

不产生干涉的条件为

R≤rt.

(30)

3)全局干涉产生和避免.全局干涉主要通过距离法判断[16].如图12所示，刀具球部中心到刀柄的距离为L，刀具轴线上的任意一点可表示为

rG(λ，ζ)=LG，K+ζtG，λ.

(31)

式中：0≤ζ≤L；LG，K表示点LG，K的位置矢量.

铣刀轴上任意一点到齿廓的距离表示为

h1(λ，ζ)=|rG(λ，ζ)-rG(α)|.

(32)

最小距离表示为

h1min=minζ，λ，α|rG(λ，ζ)-rG(α)|=R.

(33)

图12 全局干涉判断

根据式(33)求出满足要求的刀具偏角λ1min. 避免产生全局干涉，要求λ≥λ1min. 图12中刀轴上的P2点和齿面上的P3点构成了两者之间的最短距离，该距离小于R，产生了明显的全局干涉，需要调整刀倾角λ，调整的角度Δλ计算式为

(34)

式中，P1，P2，P3分别表示对应点P1,P2,P3的位置矢量.

3 仿真实例

表1所示为仿真实例采用的齿轮几何参数，球头铣刀半径R=2，进给策略采用等残留高度进给. 图13所示为不产生全局干涉的刀具偏角变化范围，渐开线齿廓部分刀具偏角可行域范围明显大于齿根过渡曲线和齿根圆部分.图14所示为基于CAD实体法齿轮铣削加工中刀具和工件之间的相对位置，刀具始终位于切削齿槽内，没有产生干涉现象. 图15所示为实体法仿真后的齿廓偏差，渐开线齿廓刀具偏角λ=60°，过渡曲线和齿根圆刀具偏角λ=-20°，相邻刀位点之间的齿廓偏差一致，均小于等于残留高度h.图16所示为基于VERICUT的齿轮铣削过程仿真.机床采用图16a中Makino a77四轴卧式加工中心，图16b中齿根圆铣削设置刀具偏角λ=-20°时，铣刀和齿廓之间没有发生全局干涉现象，然而图16c中λ=-25.71°时，则产生明显的全局干涉. 上述仿真结果验证了刀具路径规划方法的可行性和有效性.

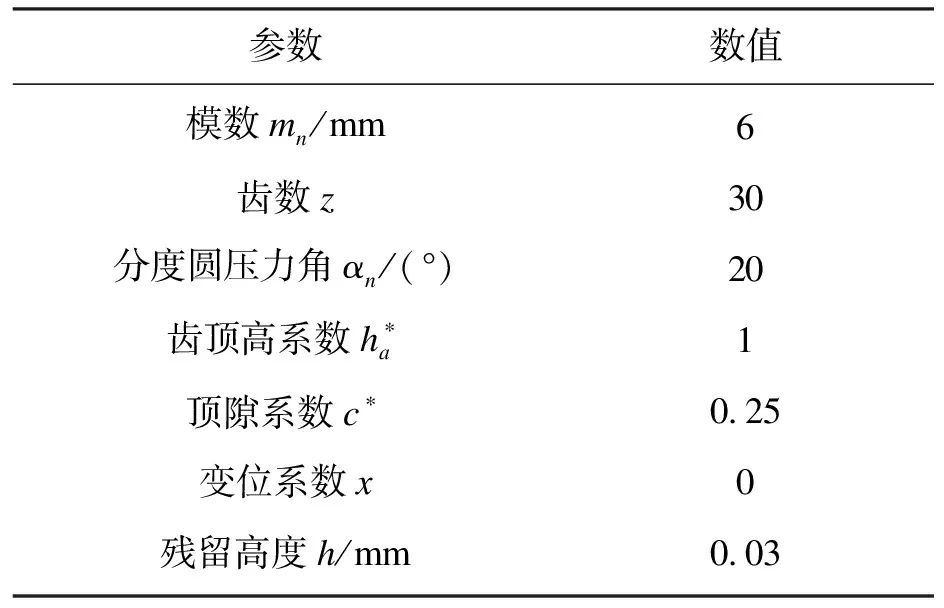
表1 齿轮几何参数

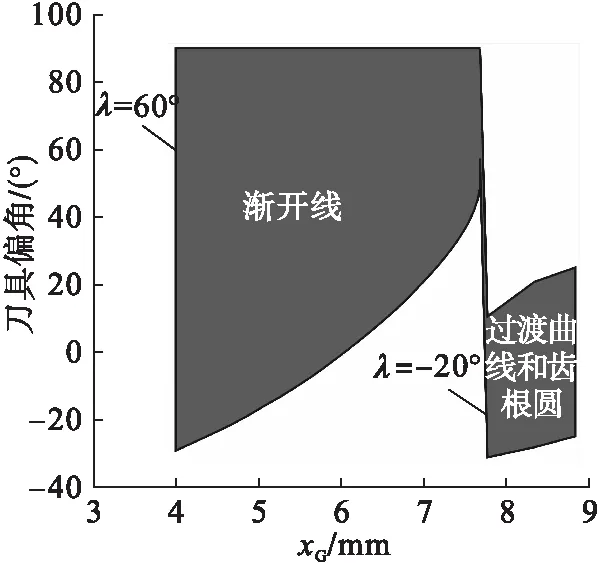
图13 无全局干涉刀具偏角

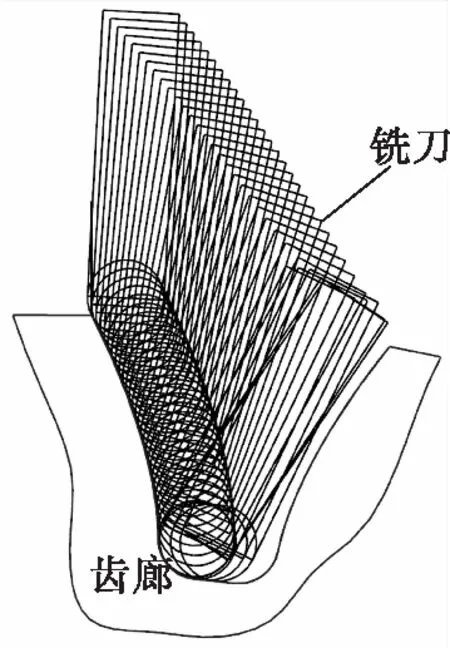
图14 铣刀与工件的相对位置

图15 齿廓偏差

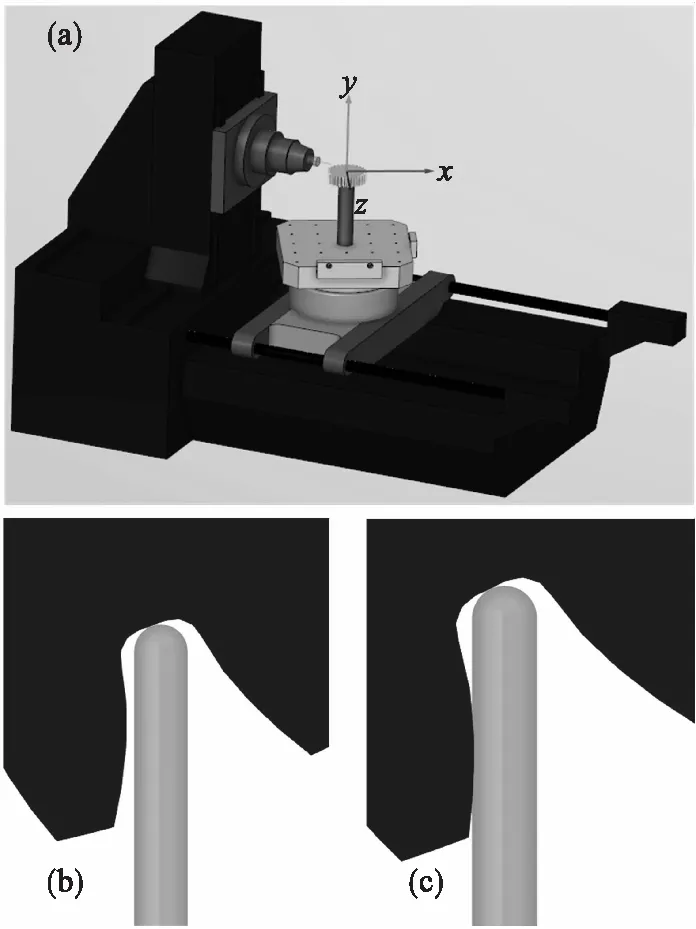
图16 全局干涉仿真

4 结 论

1) 建立齿轮包络铣削运动模型，分析渐开线齿轮齿廓的几何特性，研究等残留高度下的球头铣刀包络齿廓的刀位点计算方法.

2) 以等残留高度计算刀位点为基础，残留高度约束下，给出了等弧长、等径向进给的刀位点计算方法.

3) 针对刀具干涉情况，通过选择小于过渡曲线圆弧的刀具半径来避免；全局干涉采用距离法来确定是否干涉，给出刀具无干涉情况下的刀具偏角范围.

4) 在仿真实例的齿廓偏差曲线中，不同刀位点处的偏差一致，等于残留高度，仿真加工过程有效地避免刀具干涉. 仿真结果验证了本文所采用方法的可行性和有效性.