基于SVD-UKF的车用锂离子动力电池传感器故障诊断研究

孟德安，舒强，王建平，王艺帆，马宗钰

（1.长安大学汽车学院，西安 710062；2.公安部道路交通安全研究中心，北京 100062）

传感器作为电池系统中的数据采集单元，对电池工作状态进行监控。传感器对电池系统的正常运行至关重要，电池荷电状态（State of Charge，SOC）与健康状态的准确估计、电池的过充过放保护、做出的各项控制策略，以及对电池的故障诊断都离不开传感器的精确测量。传感器在极端环境和工况下长期使用、自身老化等原因都会导致传感器测量精度下降甚至出现故障，影响电池系统安全运行，所以应及时对传感器故障进行诊断。

对电池传感器故障诊断的研究大多基于模型方法。TRAN等通过递归最小二乘法实时估计等效电路模型参数，根据传感器故障时参数的响应性对传感器故障进行诊断。COUTO等使用双UKF生成的残差判断传感器是否发生故障，滤波器是基于简化的电化学模型。YU Quanqing 等提出使用UKF算法求出电池SOC，可以用一段时间间隔的电流累积量与估计的SOC 变化量的比估计出电池容量，用估计出的电池容量与参考容量之间的残差诊断电池故障。潘凤文等将电池模型线性化后，使用滑模观测期对新系统的输出电流进行估计，并使用基于范数的残差评价方法诊断电流传感器故障。TIAN Jiaqiang 等建立了电池组的电热模型，对模型的参数以及电压和温度值进行估计，与其他算法相比验证了粒子滤波算法对电压和温度估计的优越性，采用滑动窗口的残差学习法消除残差的异常值，通过对多种参数和状态残差CUSUM 的计算对电池系统多种传感器和电池进行故障的识别与隔离。XU Jun 等提出了一种估计电池能量状态（State of Energy，SOE）并能检测电流传感器故障的方法，通过比例积分观测器可以精确估计出电流传感器发生故障，并且可以精确估计出电流传感器发生故障时的电流误差，能够有效地获得电流传感器故障条件下电池的能量状态，经过试验验证即使在误差很严重时也能快速消除传感器故障造成的对能量状态估计的影响。之前使用这些算法的响应时间较长，并且容易受到传感器噪声和积累误差的影响。

为了去除传感器自身问题对电池诊断的干扰，本文针对单一传感器的故障诊断方法进行研究，提出通过分析模型预测电压与传感器观测电压的残差来诊断传感器是否发生故障的方法。使用UKF 算法估计电池的端电压，并提出使用奇异值分解代替平方根法分解，以解决协方差矩阵非正定导致的算法无法正常运行的问题。提出使用CUSUM 法对残差进行分析，通过监测CUSUM 的变化来判断传感器是否发生故障。本文提出的传感器故障检测方法在一些微小故障的检测中相比于传统的设定残差阈值的方法更灵敏，能更快检测出微小的数据偏移情况。

1 传感器故障类型

传感器观测的数据都不是绝对准确的，传感器的观测过程会存在扰动，从而造成一定的误差，在电动汽车实际运行中会产生颠簸、温度过高等情况，以及电池系统内传感器自身的老化、受损等原因，也会造成传感器精度降低甚至传感器失效。因此，传感器的观测误差有两部分，一种是监测过程中的自由噪声，另一种就是传感器故障造成的观测误差。

下面对几种常见的传感器故障类型进行简要介绍，以下介绍中，用f表示传感器故障产生的误差，用y表示传感器监测的信号值，用表示真实的信号值，用表示监测过程中的自由噪声。

传感器信号固定偏差故障是指测量信号与真实信号之间相差一个不变的常数值，即f= a，y=+ a +，a为常数。

传感器信号漂移偏差故障是指测量信号与真实信号相比有一个随时间线性变化的偏差，即f=b ×(-)，y=+ b ×(-)+，其中，b 为常数，为传感器故障发生的时间。

传感器增益故障是传感器测量的信号值出现倍数变化，表现形式为信号的整体偏移，则y=(1 +k)+，k为常数时为恒增益故障。

图1是传感器发生上述3 类故障时，对正弦信号的观测结果，在第5 s 时传感器发生故障，其中蓝色信号值表示实际信号值，红色信号值表示出现故障之后传感器测出的信号值。下文主要对这3 类传感器故障进行诊断。

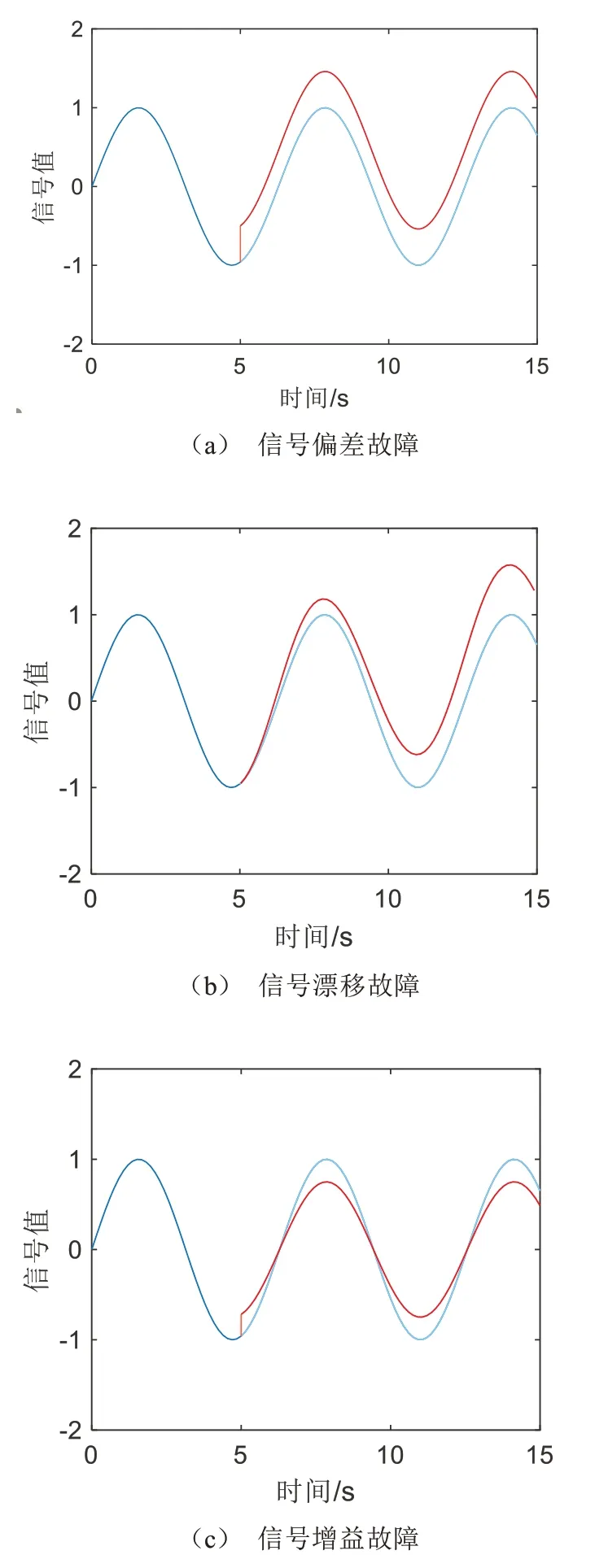
图1 传感器常见故障

2 基于SVD-UKF的传感器故障检测

在实际工况中，传感器的观测数据和电池模型都会存在一定的误差，并且电池模型SOC估算部分采用的安时积分法需要精确的SOC初值。本文采用基于UKF 算法对传感器的故障进行诊断，UKF 算法可以过滤掉系统噪声和观测噪声造成的影响，但无法过滤传感器故障时出现的较大误差带来的影响。传感器测得的电压信号与估计的电压信号对比生成残差，通过对残差分析判断传感器是否出现故障。

2.1 UKF算法

卡尔曼滤波被广泛应用于线性系统中，然而针对电动汽车锂离子动力电池这种非线性系统，可以使用UKF 算法对动力电池的状态量与端电压进行估计。

UKF算法仍以卡尔曼滤波算法为框架，是用无迹变换（Unscented Transformation，UT）这种统计线性化方法让非线性系统方程适用于卡尔曼滤波算法。典型非线性离散系统的状态方程和观测方程分别如式（1）～（2）所示：

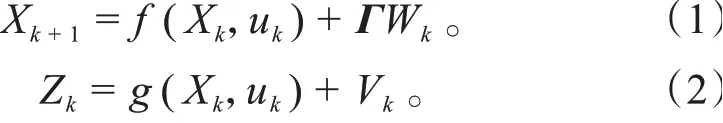
式中：X为系统的状态向量；X为下一个时刻的系统的状态向量；u为控制输入量；为系统噪声驱动矩阵；W为过程噪声，表示系统误差；Z为系统的观测向量；V为观测噪声；、为非线性传递函数。

UKF的思想是近似概率密度的方式相比于近似非线性函数更简单。例如，对于式（1）的状态方程与式（2） 的观测方程，UKF 算法并非对(X，u)与(X，u)进行近似线性化，而是对(X，u)与(X，u)的概率分布进行近似，UKF算法不需要对矩阵求偏导这样复杂的计算过程，估计精度可以保证至少达到二阶泰勒展开的精度，而且不需要大量的计算，适合本文提出的电池模型。

显然，用概率密度的方式求出函数的均值和方差是十分复杂的，UKF 算法通过UT 变换近似表征(X，u)与(X，u)的概率分布。对于非线性函数=()，UT 变换的基本原理如下：假设是维向量，已知的均值为ˉ，方差为P，经过UT 变换可以得到2+1 个sigma 点χ，并且可以求出对应的权值w，将sigma 点代入函数=()之后将得到的值进行加权求和，计算出加权均值与方差，用计算出的结果近似表征非线性变换后的概率分布，即用来近似表征的均值与方差。下面对UT 变换所需的公式进行简单介绍，首先对2+1 个sigma 点进行构建，如式（3）所示。

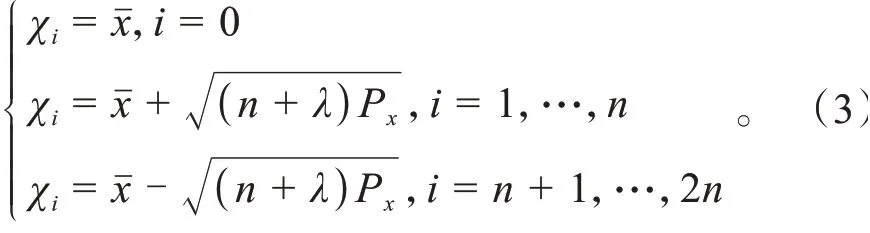
相对应的权值为：

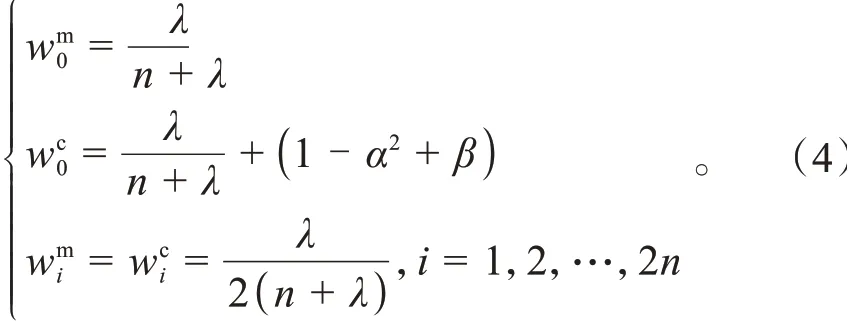
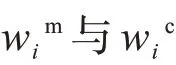
2.2 奇异值分解

在UKF 算法运行过程中，协方差矩阵一般都为正定矩阵。但是由于计算机的计算精度有限，算法更新迭代过程中的计算和求逆过程会丢失精度，还有噪声等未知因素，都会造成协方差矩阵非正定的问题。在算法运行中需要对协方差矩阵用平方根法进行分解，这要求协方差矩阵P为正定矩阵，否则算法无法正常运行。使用奇异值分解（Singular Value Decomposition，SVD）来替代平方根法分解可以有效地解决这个问题，用SVD 的矩阵不要求为方阵，而且SVD 算法有较高的精度和稳定性。假设矩阵是一个×阶的矩阵，对矩阵进行SVD，则：

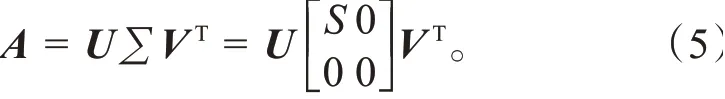
式中：为×阶矩阵；为×阶矩阵；为×阶矩阵。

当用SVD 替代平方根法对P进行分解时，生成的sigma点也相应做出改变，此时式（3）变为：

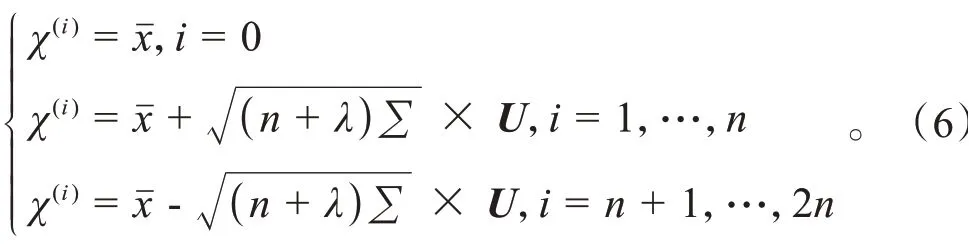
2.3 奇异值分解无迹卡尔曼滤波算法流程

首先，建立锂离子动力电池系统模型，得到离散化的锂离子电池模型的数学方程，如式（7）所示。

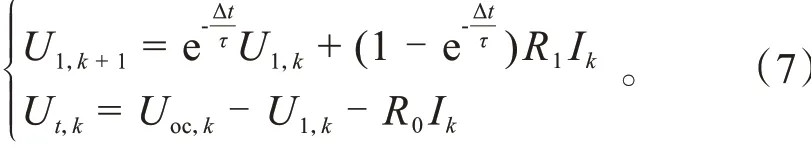
式中：Δ为电池数据的采样时间间隔，s；为时间常数；I为时刻的电流，A；为时刻的开路电压，V；U为时刻的端电压，V；为时刻的极化电压，V；为极化内阻，mΩ。

由式（7）可以得到锂离子动力电池的状态方程和观测方程。

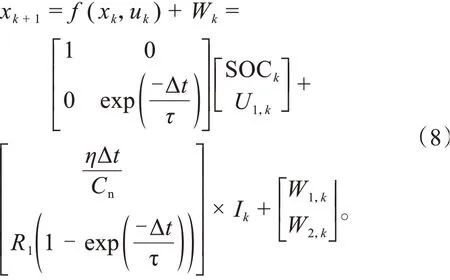
式中：W为过程噪声，V；Δ为电池数据的采样时间间隔，s；τ 为时间常数；x=[SOC，]为锂电池系统的状态向量；SOC为时刻的SOC 值；为时刻的极化电压，V；为充放电效率；表示电池容量，Ah；为电池的极化电阻，mΩ；I为电池充放电电流，A。

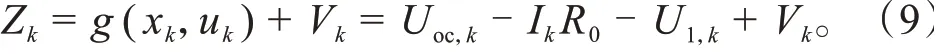
式中：系统观测量Z为锂电池的端电压，V；为时刻的开路电压值，V；为欧姆内阻，mΩ；u系统的控制输入量，V；I为传感器观测到的电流，A；为时刻的极化电压，V；V为观测噪声，V。

式中：为开路电压值，V；该等式是通过OCV试验数据拟合SOC关于的六次多项式得出的。

使用SVD-UKF算法流程如下。

（1）状态向量及协方差矩阵初始化：

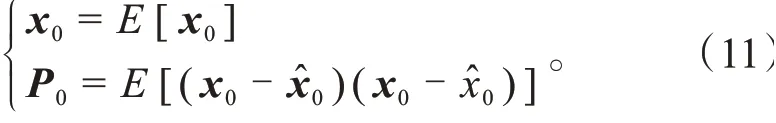
式中：为状态向量；为协方差矩阵。

（2）在时刻对上一时刻滤波后的进行一次SVD-UT变换并生成sigma点集：

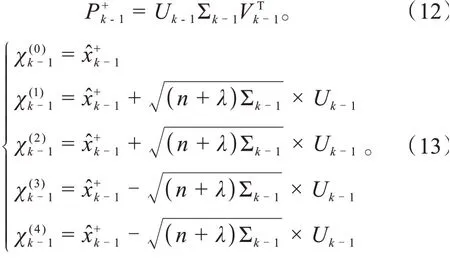
（3）sigma点状态预测：

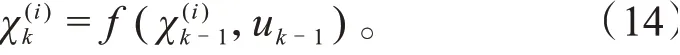
（4）计算估计的状态向量在当前时刻的均值与方差：

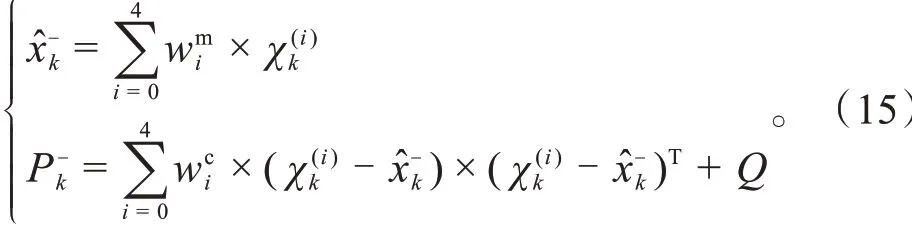
（5）对步骤4 中的先验估计再进行一次SVDUT分解，生成sigma点集：

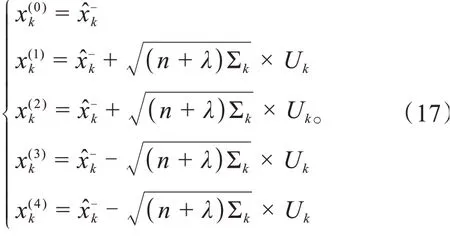
（6）sigma点观测值预测：

（7）计算观测预测值的估计均值、协方差矩阵：

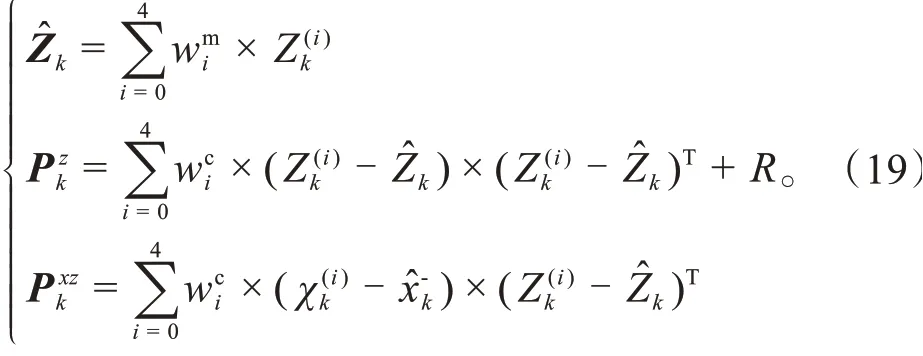
（8）计算无迹卡尔曼增益：

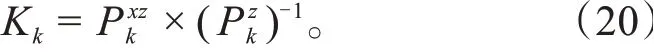
（9）系统当前时刻状态向量估计值与协方差更新：

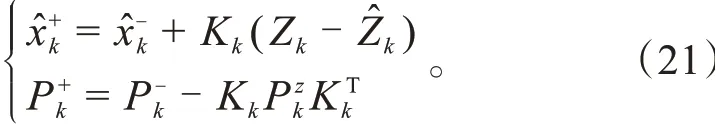
式中：Z为时刻传感器读入的一个观测值。

SVD-UKF算法的流程图，如图2所示。在计算过程中，通过对观测值的预测得到̂实现了对电池端电压的估计，通过对状态向量的估计与更新过程得到了SOC的估计值，解决了在无法精确得知初始SOC值的条件下，估计端电压造成估计值误差较大的问题。采用上述算法流程估计出电池的端电压之后，通过与传感器测得的端电压生成的残差进行分析来诊断传感器故障。下面对算法的结果进行分析以及传感器的故障诊断方法进行介绍。

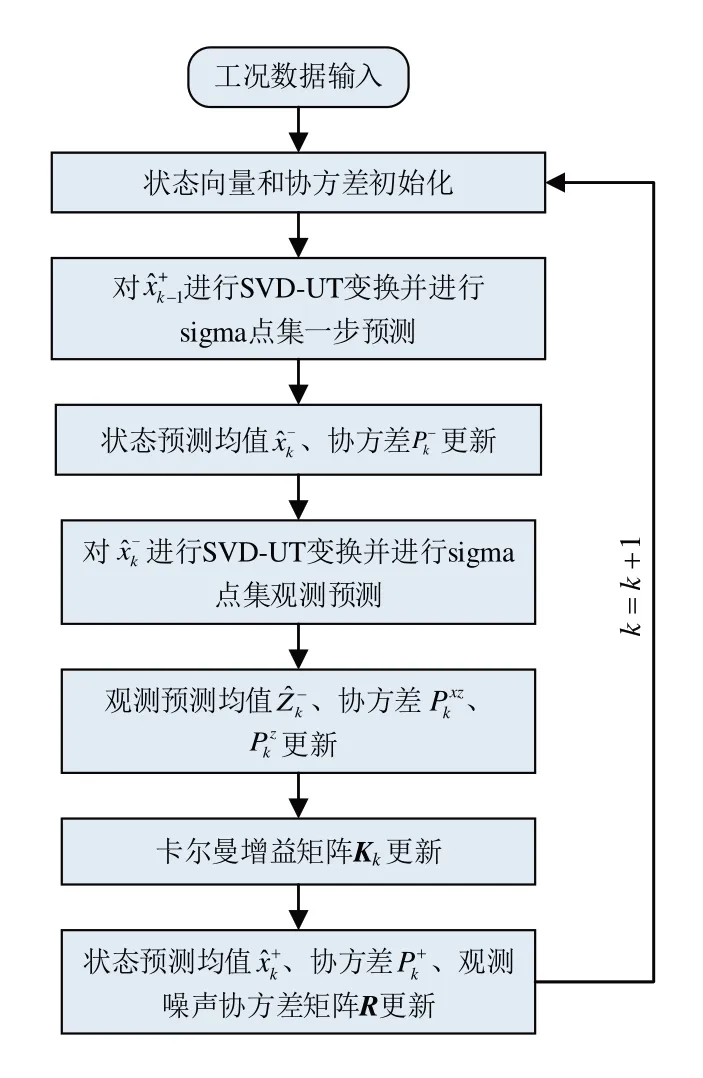
图2 SVD-UKF算法流程

2.4 基于累积和的残差评价方法

CUSUM 是一种异常检测算法，这种算法可以将过程中十分微小的量的变化累加起来将其放大。假设系统观测数值与预测值的残差为e()，系统正常时残差的概率分布为(e())，系统故障时残差的概率分布为(e())，设累积和的初始值(0) = 0，令

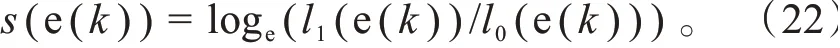
式中：(e())为系统故障时残差的概率分布；(e())为系统正常时残差的概率分布；(e())为故障时和正常时残差的概率分布的对数比。

则CUSUM：

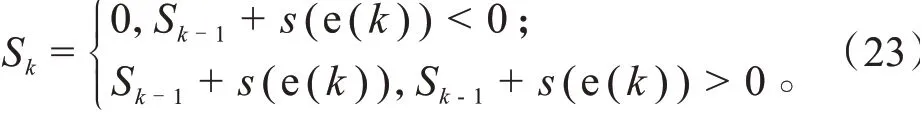
在实际过程中，(e())和(e())可能是未知的而且计算复杂，参照文献［15］，为取代上述(e())，提出：

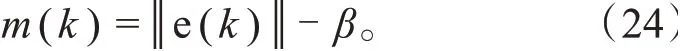
用()作为CUSUM 算法的检测序列，其中β为一常数。在系统没有发生异常情况的状态下，式（22） 算出的结果应为负值，所以()的均值(())应小于0。在没有故障的情况下，经过对图4f 中的残差进行分析计算，用SVD-UKF 算法得到的端电压残差均值约为0，并且经过计算验证大部分残差数据都分布在3倍方差范围内。

为了保证(()) < 0，设残差为，的取值可以设置在3左右，这样大部分的()数值都会小于0。式（23）转变为式（25）。

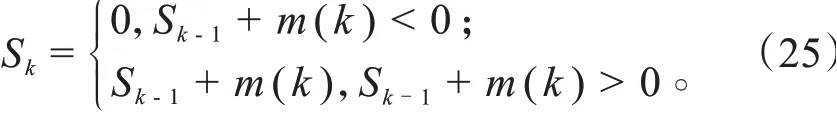
再根据S设置报警阈值thre，当S> thre 时系统报警，传感器处于故障状态。

2.5 传感器故障诊断流程

传感器故障检测的流程图，如图3所示。

图3 传感器故障检测流程

3 算法效果验证

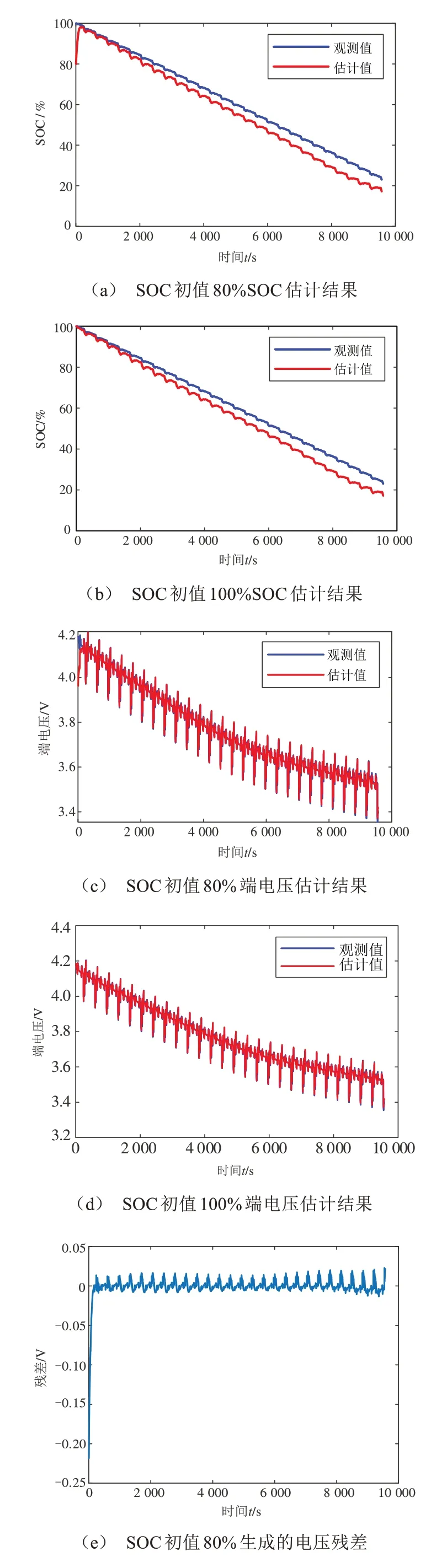
首先对上述方法进行验证，本文使用DST工况作为电池系统传感器故障的验证工况，工况数据为实验室获取的DST工况数据，锂离子动力电池的状态方程和观测方程所需数据用三星INR-18650-20R电池试验测得数据。在SOC 真实初值为100%的情况下，将SVD-UKF 算法SOC 初值设置为80%和100%时，SOC 和端电压的估计值以及电压残差如图4所示。

图4为使用SVD-UKF 算法得到的估计结果，可以看出估计的SOC值较准确，可以比较真实地反映SOC 的变化情况，即使在SOC 初值设定为80%，且与真实值偏差20%的情况下，也能快速收敛到真实值。由图4e 可知，在SOC 初值错误的情况下，端电压的估计值也能快速收敛到真实值，并且SOC初值设定正确时的电压残差和SOC初值存在偏差收敛后的电压残差都很小，都围绕0 值上下波动，适合用来分析传感器是否发生故障。本章用SOC初始值正确的情况来诊断传感器故障。

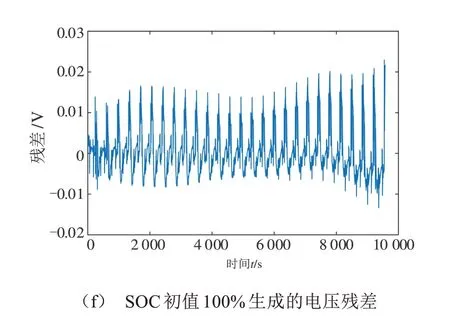
图4 SVD-AUKF估计结果

设电池电流放电为正，在4 000 s 后对DST 工况的电压和电流数据分别注入-0.03 V和+0.5 A的信号偏差故障来模拟传感器发生故障的情况，则出现故障的电压电流信号图，如图5所示。

图5 传感器故障测得信号

由于在电池系统中，电压传感器和电流传感器基本上不会出现同时出现故障的情况，所以主要研究电池系统中电压传感器或者电流传感器单独出现故障时的传感器故障诊断。当电压传感器和电流传感器分别出现图5 所示的信号偏差故障时，上述算法预测得到DST工况下的电池端电压与传感器测得的电压生成的残差，如图6所示。

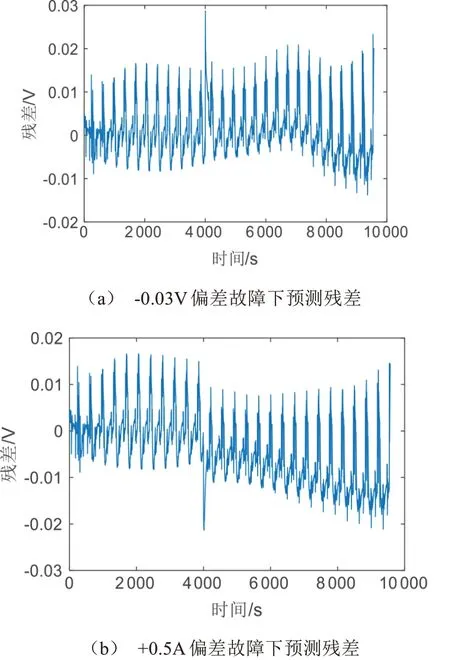
图6 传感器故障下的预测残差

由图6 可知，虽然在第4 001 s 开始对电压和电流数据注入了故障，但是发生上述信号偏差故障时，运用SVD-UKF 算法预测电池端电压得到的残差值，除了在故障开始注入的时刻增大之外，其余时刻没有明显变化。电流传感器发生信号偏差故障后SVD-UKF 生成的残差值相较于传感器正常时SVD-UKF 生成的残差有略微的偏移。可以对残差设定阈值来检测传感器是否存在故障，但是使用残差来进行判断，对于微小的故障可能会出现漏判的情况，传感器噪声、模型误差以及各种不确定因素也可能导致出现故障误诊的现象。本文提出使用CUSUM 分析残差对传感器的故障进行检测的方法。

对传感器故障进行检测，针对本文算法的参数设置，根据对电池进行多次试验，设定= 2.5。警阈值thre = 0.05。在传感器正常情况下用DST 工况数据进行检测，结果如图7所示。

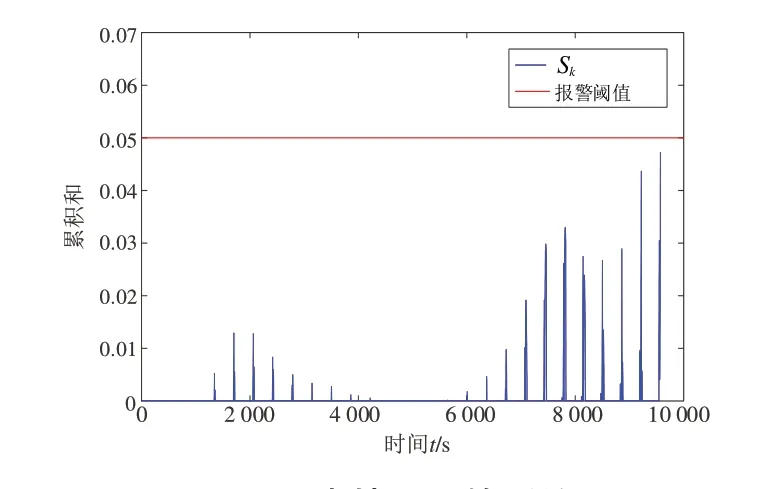
图7 正常情况下检测结果

首先对传感器偏差故障进行检测，在第4 001 s分别对电压传感器和电流传感器注入－0.03 V 和＋0.5 A 的信号偏差故障，生成的预测残差如图6 所示，检测结果如图8所示。

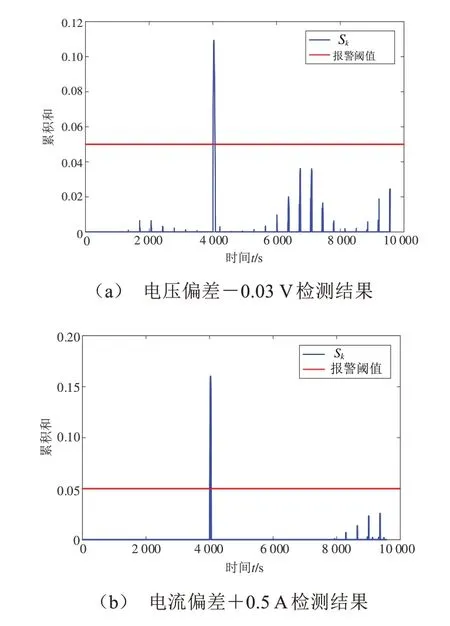
图8 传感器信号偏移故障检测

由于在偏差故障发生的时刻观测电压突然发生变化而预测电压需要一定的时间做出反应，所以残差在此刻出现明显的异常取值，在注入故障之后，S很快就超过了报警阈值，电压传感器在出现故障后的第4 s、电流传感器在出现故障后的第6 s 分别检测到了故障。

以电流传感器为例，进行传感器信号漂移故障检测。在第4 001 s 时，对电流传感器注入随时间变化的信号漂移故障= b ×(-)，将电压传感器故障和电流传感器故障的时间变化的偏差都设为b＝－0.000 1，生成的残差及检测结果如图9～10所示。

由图10 可知，电流传感器注入信号漂移故障后，经过2 724 s，在第6 725 s 时发现故障。此后，根据不同的b 取值对比发现， b 取值越大，该方法检测到故障的速度越快。而用残差阈值的方法发现，如果对图9 的残差设定为－0.015 V 和＋0.025 V的阈值，在第7 078 s时可以检测出故障。

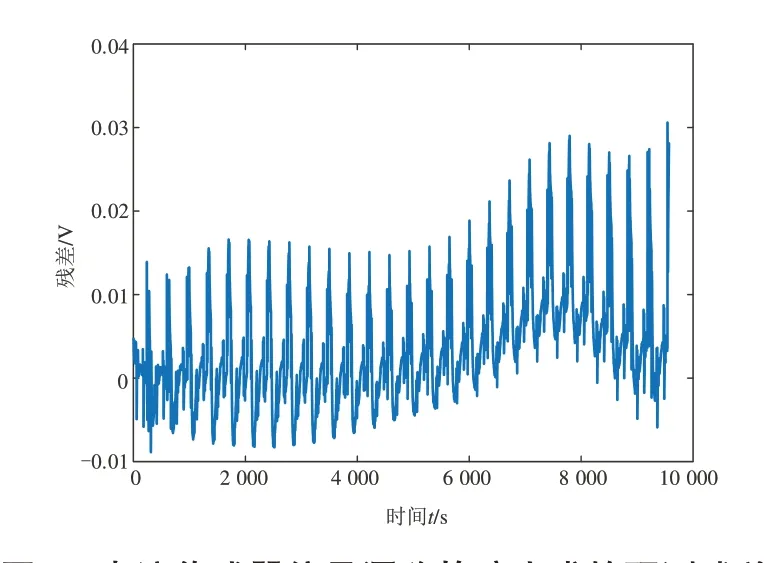
图9 电流传感器信号漂移故障生成的预测残差

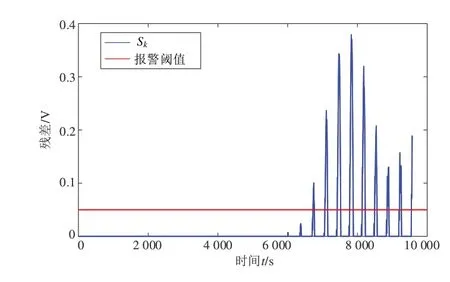
图10 电流传感器信号漂移故障检测结果

以电流传感器为例，进行传感器信号增益故障检测。4 000 s后，用电压传感器观测到的数据和电流传感器观测到的数据都乘以1.15来模拟传感器增益故障，电流传感器出现增益故障时生成的残差和检测结果，如图11和图12所示。

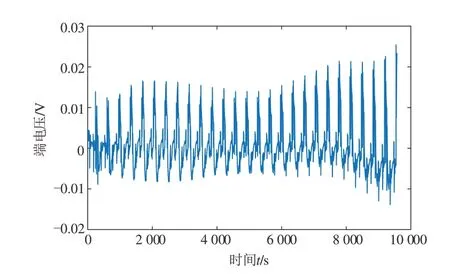
图11 电流传感器增益故障生成的预测残差

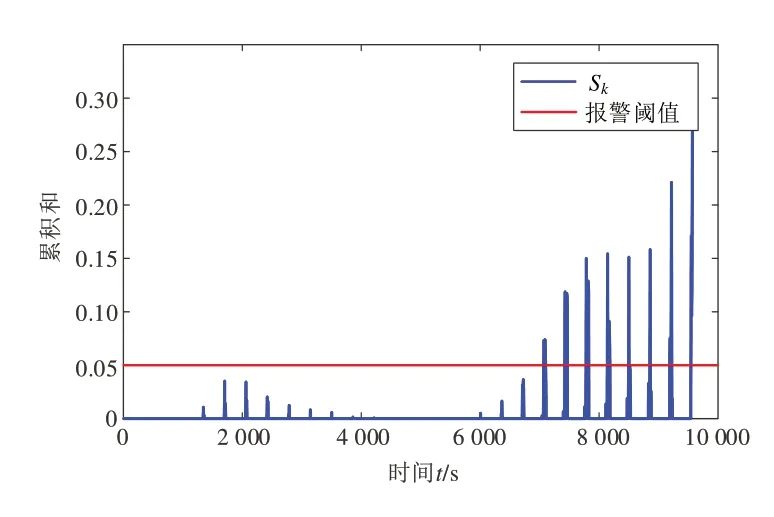
图12 电流传感器增益故障检测结果

在电流传感器发生故障后，电压残差与电流传感器未发生故障时相比变化不大，运用该方法在7 505 s 检测到传感器故障，如果用残差阈值进行检测，要在9 543 s才能检测出传感器发生故障。

以上分析可知，本文提出的传感器故障检测方法在一些微小故障的检测中相比于传统的设定残差阈值的方法更灵敏，能更快检测出微小的数据偏移情况。

4 结论

本文主要研究车用动力电池的传感器故障诊断方法，提出用预测的电池端电压与传感器观测电压生成的残差来进行传感器故障的诊断。

本文提出使用UKF 算法对电池端电压进行预测，解决在锂离子动力电池建模和传感器观测值中都存在一定误差的问题。针对UKF 算法在分解协方差矩阵时，协方差矩阵非正定导致算法无法正常运行的问题，提出使用SVD来代替平方根法分解。

用DST 工况作为传感器故障诊断的检验工况。提出用CUSUM 法对电压残差进行分析，并针对故障时和正常工作时电压残差的概率分布不确定性的问题，对算法进行改进调整。用该算法对3 类常见的传感器故障进行检测。由检测结果可知，相比于残差阈值法，该方法有更高的灵敏度和准确性。