基于多相耦合的钢制双层LNG储罐外爆响应特性分析

丁宇奇，谢 清，芦 烨，杨 明，张佳贺，赵砚峰

(东北石油大学 机械科学与工程学院，黑龙江大庆 163318)

0 引言

LNG储罐储存的液体具有易燃、易爆、易扩散等特点，发生泄漏后，遇到意外点火源会导致燃烧爆炸，带来巨大的损失。为了减小爆炸事故造成的伤害，需要对外爆载荷作用下的钢制双层LNG储罐的破坏问题进行研究[1-3]。

外爆载荷作用下钢制双层LNG储罐的破坏，主要涉及爆炸载荷的传递和多相耦合作用的结构响应。针对爆炸载荷的传递问题，朱东等[4-5]使用侵蚀接触算法建立了钢储罐结构的有限元分析模型，分析在爆炸载荷下撞击物对储罐的动力响应和失效模式。胡可等[6-7]使用ALE算法模拟爆炸载荷在空气和钢储罐之间的载荷传递，建立了钢储罐外部爆炸载荷的有限元分析模型，分析了储罐外壁面上的爆炸压力分布规律。翁大根等[8-9]采用流固耦合算法模拟爆炸载荷在空气、外罐和储液之间的载荷传递，对接触爆炸作用下的特大型LNG储罐的动力响应进行了数值模拟分析。针对多相耦合作用的结构响应研究，路胜卓等[10-11]通过模型试验与数值模拟结果对比，考虑乙炔/空气混合气体-储油罐-罐内液体之间的多相耦合作用，探讨了浮顶油罐在可燃蒸气云爆炸冲击作用下的变形过程和破坏机理。丁宇奇等[12]建立管道、内部流体与土体的多相耦合模型，得到了管道内有无流体对管道响应的影响情况，得出充液管道径向变形峰值比空管径向变形峰值降低10%左右的结论。胡陈等[13-15]为了探究储罐液位对爆炸响应的影响，建立空气-储罐-石油的多相耦合模型，分析了储罐在爆炸荷载作用下的结构动态响应。

通过现有研究发现，对于钢制双层LNG储罐，考虑了外罐与罐内液体之间的爆炸载荷传递问题，而未对外罐、保冷材料、内罐和罐内流体之间的爆炸载荷传递问题进行研究。因此，本文以钢制双层LNG储罐为研究对象，考虑外罐、保冷材料与内罐之间的载荷传递作用和罐内流体与内罐之间的相互作用，建立一个探究保冷材料不同状态和不同液位因素的空气-储罐结构-罐内流体多相耦合有限元模型，采用侵蚀和面面接触算法来分别模拟保冷材料完整和破碎消失两种状态，对爆炸冲击波的载荷计算、储罐结构的固有频率以及响应变化情况进行分析。本文研究成果可以为钢制双层LNG储罐在外爆载荷作用下的响应分析提供理论参考。

1 钢制双层LNG储罐外爆载荷传递的多相耦合方法

1.1 钢制双层LNG储罐的外爆载荷多相耦合计算方法

由气体泄漏等引发的爆炸在空气域中形成爆炸空腔，爆炸产生的冲击波会通过空气、储罐结构与罐内流体耦合界面作用到储罐上，使储罐发生变形和破坏。将这一过程分为4个阶段(如图1所示)：阶段1为爆炸冲击波刚传到储罐结构，外罐开始发生变形，保冷材料中膨胀珍珠岩开始发生破碎，颗粒向两边移动；阶段2为随着爆炸冲击波进一步传递，外罐和内罐变形逐渐变大，保冷材料中膨胀珍珠岩的破碎程度逐渐变大至完全破碎，此时呈现出颗粒向两边集中、中间部位颗粒缺失的现象，而PUF(聚氨基甲酸乙酯泡沫)块和弹性玻璃棉毡的应变逐渐增大，随后发生失效；阶段3为外罐开始发生破坏；阶段4为外罐破坏变大，内罐开始发生破坏。

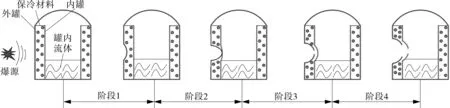
图1 储罐结构变形与破坏过程示意

空气-储罐结构与内罐-罐内流体采用流固耦合的方式进行计算[16]，外罐-保冷材料-内罐之间采用罚函数耦合的方式进行计算，耦合界面载荷传递过程如图2所示。

图2 爆源与罐体各部分之间的载荷传递示意

首先，爆炸冲击波使空气产生压力，传递到外罐结构上,如式(1)所示。

pf=Hfsps

(1)

式中,pf为空气压力向量；Hfs为空气域到外罐结构域的传递矩阵；ps为外罐结构的压力向量。

外罐结构受到空气的压力会产生变形，反馈给空气,如式(2)所示。

ds=Hsfdf

(2)

式中,ds为外罐结构的位移向量；Hsf为外罐结构域到空气域的传递矩阵；df为外罐结构域变形后空气边界处的位移向量。

接着，载荷传递至外罐与保冷材料之间会产生一个接触力Fa，在外罐接触面穿透保冷材料目标面时会产生一段穿透距离xp，通过下式可以使力与变形之间达到平衡：

Fa=kaxp

(3)

式中,ka为罚函数刚度。

随后，载荷传递至保冷材料与内罐之间会产生一个接触力Fb，在保冷材料接触面穿透内罐目标面时，会产生一段穿透距离xp1，通过下式使力与变形之间达到平衡：

Fb=ka1xp1

(4)

式中,ka1为罚函数刚度。

最后，载荷传递至内罐，使内罐产生变形，反馈给罐内流体,如式(5)所示。

ds1=Hs1f1df1

(5)

式中,Hs1f1为内罐结构域到罐内流体域的传递矩阵。

罐内流体的压力传递到内罐结构上,如式(6)所示。

pf1=Hf1s1ps1

(6)

式中,pf1为罐内流体的压力向量；Hf1s1为罐内流体域到内罐结构域的传递矩阵；ps1为内罐结构的压力向量。

为了验证本文建立的双层储罐外爆载荷多相耦合计算方法的准确性，与文献[17]中的试验进行数值模拟对比验证。文献[17]中试验时采用的钢制模型罐为丙烷低温储罐，外罐直径70 m、高度35.5 m，内罐直径67.6 m、高度31.92 m，高度方向的厚度从20～51 mm不等。试验中测试的储罐是全尺寸的1∶70小比例模型，恒定壁厚为1 mm，材料为45#低碳钢。将空气和乙炔注入点火系统和装载罐的容器中，然后可燃混合物在喷射结束后2 s,由火花塞自动点燃;点火引起混合物爆燃，火焰通过管道传播并到达装载平台中的装载罐;最后，装载罐中混合气体的爆燃产生爆炸波，爆炸波通过装载罐的开口传播，并在罐表面施加爆炸载荷，试验装置及储罐的形貌如图3所示。本文基于DYNA平台，依据试验储罐参数建立储罐以及流体域(空气、TNT)的流固耦合模型，得到储罐受爆炸载荷的结构响应结果，限于篇幅，只给出储罐受到爆炸冲击波作用后的形貌，如图4所示。将试验与数值模拟两种方法得到的结果进行汇总，如表1所示。

图3 试验装置及储罐的形貌

图4 数值模拟储罐的形貌

表1 试验结果与数值模拟结果对比数据

通过图3,4和表1可以看出，本文数值模拟计算的峰值压力、峰值变形与试验的相对误差分别为4.3%和3.0%。因此，本文建立的双层储罐的外爆载荷多相耦合的计算方法具有合理性和准确性。

1.2 考虑保冷材料破碎失效的爆炸冲击波传递

保冷材料包括PUF块、膨胀珍珠岩和弹性玻璃棉毡三种材料。随着外罐的变形，保冷材料中PUF块和弹性玻璃棉毡会随着应变的增大发生失效，而保冷材料中膨胀珍珠岩会移动和消失。当保冷材料未发生破坏时，爆炸冲击波在外罐和内罐之间通过保冷材料进行传递；当保冷材料破碎失效后，爆炸冲击波将直接作用到内罐，如图5所示。

当外罐发生破坏后，爆炸冲击波将穿透保冷材料作用在储罐表面，其爆炸冲击波压力为pf2，此时在内罐表面有：

pf2=Hf2s2ps2

(7)

式中,pf2为空气压力向量；Hf2s2为空气域到内罐结构域的传递矩阵；ps2为内罐结构的压力向量。

图5 保冷材料完全破碎状态下的载荷传递过程

内罐结构受到爆炸压力会产生变形，并反馈给空气,如式(8)所示。

ds2=Hs2f2df2

(8)

式中,ds2为内罐结构的位移向量；Hs2f2为内罐结构域到空气域的传递矩阵；df2为内罐结构域变形后空气边界处的位移向量。

2 基于多相耦合的钢制双层LNG储罐有限元模型的建立

本文研究的钢制双层LNG储罐主要包括：空气域、储罐结构域(外罐、保冷材料、内罐和地基)和罐内流体域三部分。内罐吊顶等结构对内罐主要起到密封作用，对于外罐相当于施加了集中载荷作用，但这并不影响内外罐外爆响应特性，因此，文中研究未考虑内罐吊顶结构。其中空气域尺寸为76 000 mm×38 000 mm×50 000 mm，罐内流体域高度为14 350 mm(以半罐为例)，储罐外爆载荷采用TNT当量法进行模拟。钢制双层LNG储罐各部分结构与材料参数见表2。

表2 储罐各部分材料与结构参数

为了建立有限元模型，空气域采用实体单元Solid 164，该单元可以通过空气物质材料模型来描述空气的特性，其本构方程为：

P1=f0+f1μ+f2μ2+f3μ3+(f4+f5μ+f6μ2)E1

(9)

式中,P1为空气压力，MPa；f0～f6为空气状态方程参数；μ为相对密度，μ=ρ/ρ0-1(ρ，ρ0为空气当前密度和空气初始密度，kg/m3)；E1为空气材料内能，J/m3。

空气材料参数的具体数值见表3。

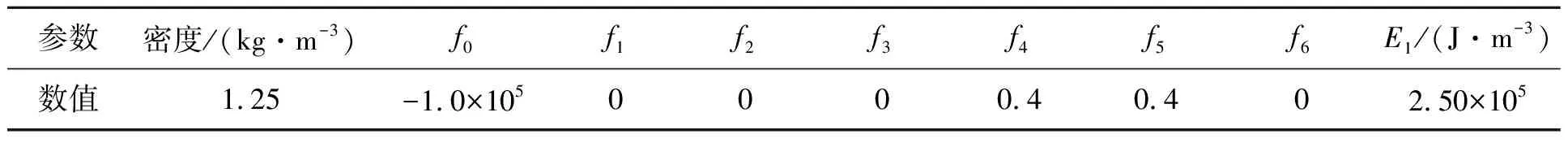
表3 空气材料参数

内罐和外罐采用壳单元Shell 163，该单元可以应用Johnson-Cook强化模型来描述储罐的塑性性能，其本构方程为：

(10)

本文不考虑温度影响，储罐的材料参数见表4，罐内流体的材料参数见表5，保冷材料的参数见表6[18-20]。

表4 储罐结构材料参数

表5 LNG储液的材料参数

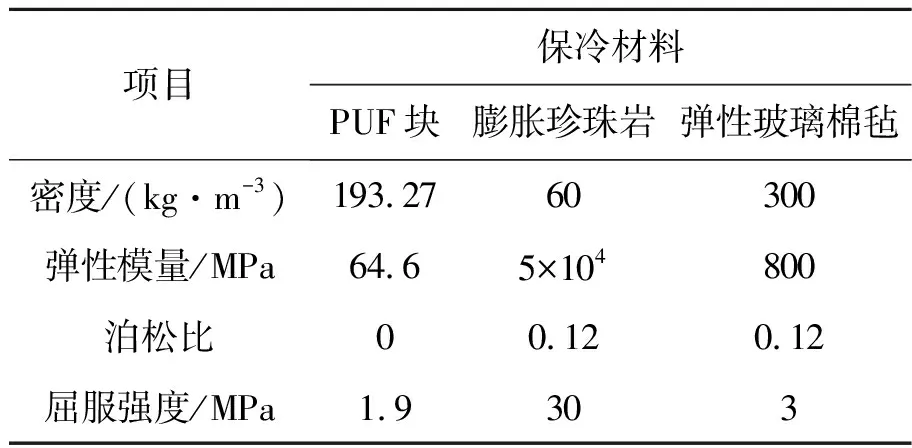
表6 保冷材料的材料参数

保冷材料采用实体单元Solid 164，该单元通过随动硬化材料模型，可以考虑应变率的影响。地基采用实体单元Solid 164，该单元通过土壤泡沫材料模型可有效模拟土壤。罐内流体域采用实体单元Solid 164，该单元通过液体物质材料模型来描述液体的特性，其本构方程为：

(11)

建立钢制双层LNG储罐的多相耦合有限元模型如图6所示，储罐结构域采用拉格朗日网格描述，罐内、外空气域和罐内流体域采用欧拉网格描述。为保证数值计算模型的可靠性和精度，分别对外罐、内罐以及流体域单独开展网格无关性验证。其中，储罐结构单元依据单元比例限定原则划分网格，分别对储罐壁面施加指定压力，并对储罐最大应力点的应力进行监测；流体域单元依据单元尺寸限定原则划分网格，并对正对爆心10 000 mm处的压力进行监测。网格无关性验证计算结果如表7所示。

图6 钢制双层LNG储罐有限元模型

表7 储罐结构域与流体域网格无关性验证

从表7可以看出，所设置的单元比例与尺寸均保证了监测点的应力(压力)数值波动范围在5%以内。考虑计算结果的稳定性和计算时间的经济性，内、外罐结构单元比例选择1∶15，单元最大尺寸为1 000 mm，流体域单元尺寸选取600 mm。

为了计算方便，分别在距爆心2 400,3 000,3 600,4 200,4 800 mm的5个位置，布置空气域观测点A、外罐罐壁观测点B、保冷材料观测点C、内罐罐壁观测点D、罐内流体域观测点E。结合第1.1，1.2节内容，采用Euler/Lagrange耦合算法来实现空气-储罐结构和罐内液体-内罐之间的载荷传递。外罐和内罐壳单元与地基实体单元部分的接触采用面面接触算法，当罐体单元产生变形后，通过接触单元将载荷传递给实体单元。当保冷材料完整时，外罐受到的载荷先通过侵蚀接触算法传递给保冷材料，再通过该算法传递给内罐；当保冷材料完全破碎消失且外罐没发生破坏时，此时外罐受到的载荷直接通过面面接触算法传递给内罐；当保冷材料完全破碎消失且外罐发生破坏时，此时爆炸载荷通过Euler/Lagrange耦合算法传递给内罐。

为了描述外爆载荷高爆速的冲击效果和储罐结构瞬态响应，文中采用Ansys数值模拟平台中的Ls-dyna模块进行计算。根据储罐结构对称性的特点，为节省计算资源，在计算时采用半结构模型对储罐进行建模。在模型对称面上施加对称边界条件，外罐底面为刚性固定约束，内罐与内罐地基为接触边界，外罐外部空气域边界为无反射边界条件，不考虑由于阳光照射引起的储罐外壁面温升的影响因素。

3 钢制双层LNG储罐爆炸冲击波载荷的计算

3.1 在不同时刻爆炸冲击波压力传播过程

关于储罐外爆载荷，以某工程的管道泄漏为例进行计算[21]，该管道泄漏速率为7.6 kg/s，经过100 s后泄漏量为760 kg，其简化得到的TNT当量为5 600 kg。

对不同液位(空罐、半罐、满罐)下，爆炸冲击波在不同介质传播时，爆炸压力的变化情况进行计算，以半罐液位爆炸冲击波传播过程为例进行说明，图7示出不同时刻爆炸冲击波的压力传播变化云图。

图7 不同时刻爆炸冲击波的压力传播云图

从图7可以看出，点火瞬间产生的爆炸压力高达几千兆帕，最大压力位置在爆源中心处；在549 μs时，爆炸冲击波在空气传播过程中的爆炸压力数值迅速下降，压力波面积在传播过程中逐渐扩大，呈球形波面；在749 μs时，爆炸冲击波到达外罐壁并发生了反射，此时最大压力位置出现在反射区域附近；在999 μs时，爆炸冲击波传到保冷材料，由于高速气流向前运动受到抑制，下一层气流的运动也受到抑制，导致在保冷材料附近形成高压区，使得冲击波前方的压力明显大于后方的压力；在1 149 μs时，爆炸冲击波传到内罐，由于内罐对冲击波也有反射作用，使内罐附近形成的高压区范围不断增大，冲击波继续向四周低压区移动；在4 049 μs时，爆炸冲击波已传递至整个罐内液位以上部分，而在液位以下部分的冲击波压力数值几乎为0。

3.2 爆炸冲击波在不同介质中的传播特性分析

为了对比分析不同位置处压力随时间的变化情况，图8示出不同位置处的压力时程曲线，图9示出相同时刻下压力沿着爆炸冲击波传播路线的变化情况。从图8可看出，在1 000 μs左右，A点达到压力峰值128.3 MPa，随后迅速递减至0，这是由于一方面，爆炸压力在空气传播过程中是逐渐递减的；另一方面，爆炸压力在空气中受到的阻力小，传播速度快；B,C,D点都出现了二次峰值压力，且第二次峰值压力比第一次大，这是由于爆炸冲击波到达外罐、保冷材料和内罐后，使压力出现了反射增强；E点爆炸压力在4 000～5 000 μs达到压力峰值，随后逐渐递减至0，这是由于爆炸冲击波在液体传播中受到的阻力大，传播速度慢。

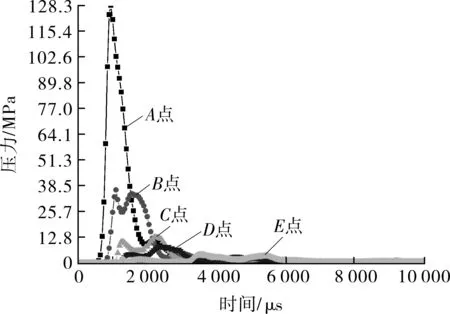
图8 不同位置处的压力时程曲线

图9 相同时刻下压力沿整条路径的变化情况

从图9可以看出，在549 μs时，爆炸冲击波在空气中传播的爆炸压力已降低至11.9 MPa；在749 μs时，爆炸冲击波到达外罐壁发生反射，使反射区域中的压力比该处自由空气中的爆炸压力大3倍左右；在999 μs时，爆炸冲击波传到保冷材料，此时的保冷材料处于完整状态，对爆炸冲击波形成了极大的阻力，使反射压力增强，压力数值达到了119.4 MPa，随着保冷材料开始发生破碎消失后，压力数值不断降低；在1 149 μs时，保冷材料完全破碎，压力数值已降为95.9 MPa，此时爆炸冲击波直接从外罐传递到内罐，由于外罐和内罐的反射作用，使得压力数值还是很大；随着爆炸冲击波的进一步传播，压力数值逐渐降低，在4 049 μs时，爆炸冲击波已到达了罐内流体，爆炸压力数值降低至0～5 MPa，这是由于爆炸冲击波在液体中传播时，液体对爆炸冲击波起到削弱作用。

为了对比不同液位下爆炸压力在不同位置处的变化情况，分别提取不同位置处的峰值压力和峰值时刻，如表8所示。

表8 不同位置处的峰值压力和峰值时刻

从表8可以看出，不同液位时，A，B，C点的峰值压力和峰值时刻相同，这是由于在3 000 μs之前，爆炸冲击波还未传到内罐和罐内流体，即A，B，C点出现峰值压力的时刻都在3 000 μs之前，所以液位的高低对空气域、外罐和保冷材料没有影响。半罐和满罐时，内罐测点D达到压力峰值的时间分别比空罐延后9.7%和12.8%，压力峰值分别比空罐减小了29%和95.9%；半罐和满罐时，罐内流体测点E达到压力峰值的时间分别比空罐延后15.5%和61.7%，压力峰值分别比空罐减小了26%和73.2%。

4 钢制双层LNG储罐的固有特性响应分析

4.1 钢制双层LNG储罐的模态分析

为了分析钢制双层LNG储罐在外爆载荷作用下的响应，对其固有特性开展研究。由于考虑设置接触后会影响结果的收敛性，故对外罐以及不同液位下的内罐分别单独计算，分别得到外罐、内罐(空罐、半罐、满罐)的一阶、二阶频率，如表9所示。可以看出，内罐(空罐)的一阶和二阶模态频率比外罐小51%；内罐(半罐和满罐)的一阶模态频率分别比内罐(空罐)小84%和81%；内罐(半罐和满罐)的二阶模态频率分别比内罐(空罐)小76%和74%，这是由于罐内液体的存在使得储罐的固有频率减小、储罐不容易发生晃动所致。

表9 钢制双层储罐的模态响应

4.2 钢制双层LNG储罐的响应特性

在瞬态动力学分析过程中，需要考虑外罐和内罐的相关阻尼参数的影响，经典Rayleigh阻尼的质量矩阵和刚度矩阵的系数计算公式[22]分别为：

α=2ξωiωj/(ωi+ωj)

(12)

β=2ξ/(ωi+ωj)

(13)

式中,α为质量阻尼系数；ξ为阻尼比，储罐为金属，ξ选取2%；ωi,ωj分别为钢制双层储罐的第一、二阶固有频率，Hz；β为刚度阻尼系数。

经计算，不同液位条件下，储罐各阻尼系数如表10所示。可以看出，内罐(半罐)和内罐(满罐)的α分别比内罐(空罐)减小了81%和78%；而内罐(半罐)和内罐(满罐)的β比内罐(空罐)增大了78%和85%。

表10 不同液位工况下储罐的α，β值

5 外爆载荷作用下钢制双层LNG储罐的结构响应

5.1 不同时刻外罐、保冷材料和内罐的破坏过程

为了模拟保冷材料破碎失效过程，根据有效塑性应变来判断保冷材料是否被破坏。当保冷材料受冲击作用时，若PUF块的有效塑性应变超过0.001，膨胀珍珠岩的有效塑性应变超过0.02，弹性玻璃棉毡的有效塑性应变超过0.04，则该处的保冷材料就会被破坏。由于储罐材料使用了Johnson-Cook强化模型来描述储罐的应变率效应，故本文采用Johnson-Cook失效准则来判定材料的破坏与否，其表达式为：

×(1+D5T*)

(14)

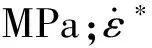
为了研究钢制双层LNG储罐的响应情况，文中以半罐为例进行说明，限于篇幅，此处仅给出不同时刻外罐、保冷材料和内罐的破坏过程。图10示出不同时刻外罐、保冷材料和内罐的表面变形情况。

图10 不同时刻外罐、保冷材料和内罐表面变形云图

由图10可以看出，文中钢制双层LNG储罐的破坏位置均为迎爆面中心，都是向内凹陷、直至发生破坏。结合第3节内容，由于材料本身有一定的抗冲击性能，在保冷材料完整时，保冷材料对爆炸冲击波的阻力很大，因此保冷材料对爆炸冲击波有一定的缓冲作用，使外罐和内罐受到爆炸压力的影响较小。在2 500 μs时，随着保冷材料开始出现破碎，导致保冷材料对爆炸冲击波的缓冲作用减小，外罐和内罐的变形逐渐增大，此时外罐最大变形已达到了1 415 mm，内罐的变形也达到了566 mm；在3 299 μs时，保冷材料完全破碎，此时外罐出现了破口，爆炸冲击波不再通过保冷材料，直接从外罐传递至内罐，内罐的变形达到了1 490 mm；在3 749 μs时，外罐破口进一步变大，内罐也开始出现了破口。

5.2 不同介质对储罐结构响应的影响

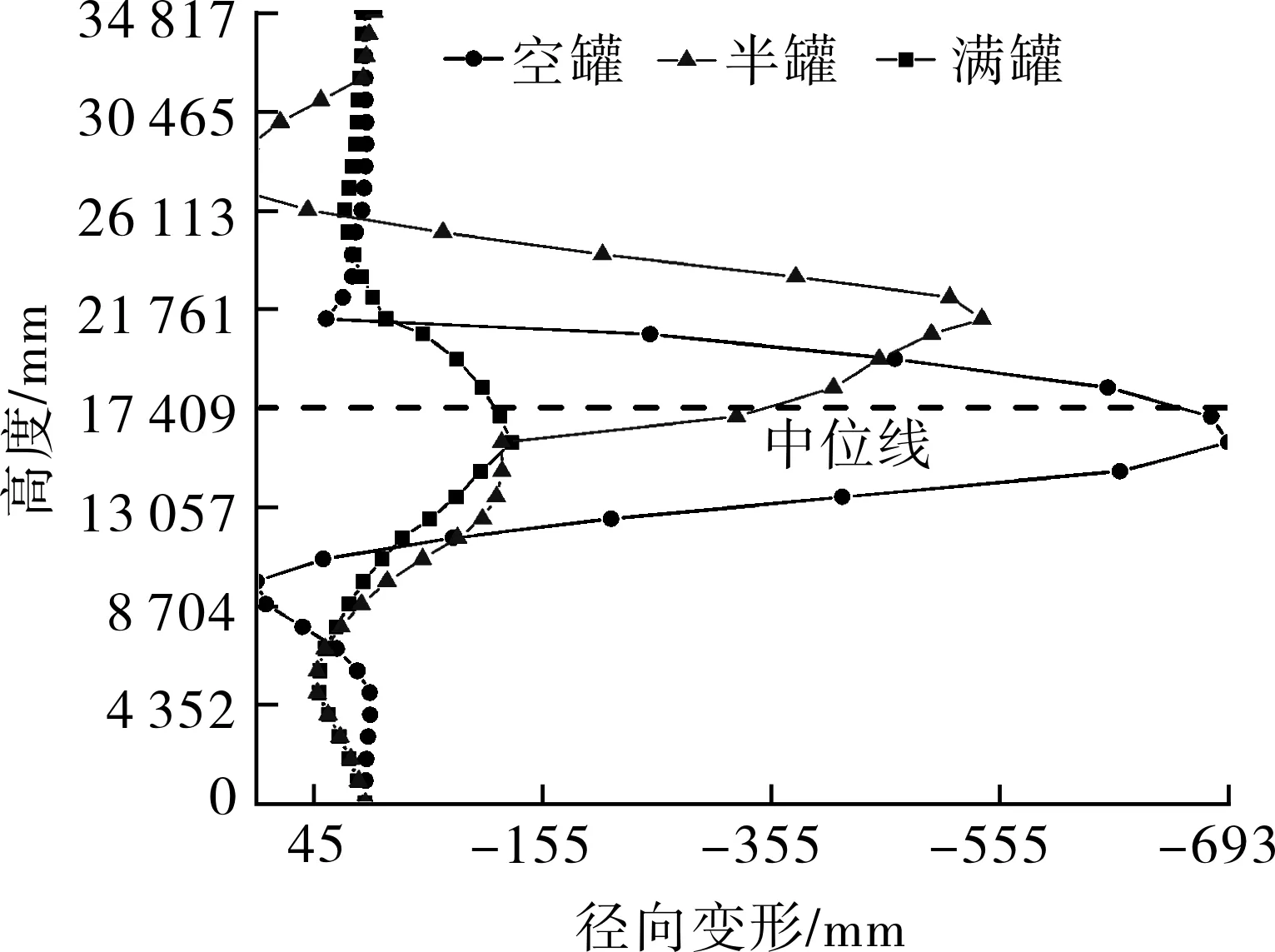
为了研究在不同液位(内罐为空罐、半罐和满罐)下，外罐和内罐沿着罐壁高度的响应情况，以爆炸发生1 749 μs时刻为例，外罐和内罐沿着罐壁高度的径向变形对比如图11所示。

从图11中可以看出，外罐和内罐的中间部位都向内凹陷，越靠近中心，向内凹陷的程度和径向变形越大。在空罐和满罐时，径向变形沿着中位线呈对称分布；而在半罐时，径向变形沿着中位线的分布呈一侧变形大、一侧变形小。在半罐和满罐时，外罐对抵抗爆炸冲击波能力都比空罐时提高了至少一倍；而在半罐和满罐时，内罐对抵抗爆炸冲击波能力比空罐时分别提高了20%和85%左右。

为了分析不同TNT炸药当量和不同液位下的储罐结构破坏的规律，储罐在破坏发生后的内外罐变形及应力变化情况如表11所示。

(a)外罐

(b)内罐

表11 储罐破坏时刻的应力和径向变形

从表11可以看出，对于相同炸药当量，在空罐和半罐工况下，外罐和内罐都发生了破坏，且半罐时，外罐和内罐发生破坏时间比空罐延迟了2倍；而满罐工况时，只有外罐发生了破坏，内罐没有发生破坏，其中外罐发生破坏时间比空罐延迟了4.3倍。从外罐破坏时刻的径向变形可以看出，满罐和半罐工况时，外罐的径向变形是内罐的1.6～2.3倍，空罐时，外罐的径向变形是内罐的2.7倍。对于空罐来说，由于爆炸冲击波在空气中传播受到的阻力小，导致储罐发生破坏时间短，变形大；对于半罐来说，由于爆炸冲击波在液体传播中受到的阻力很大，同时液体也会吸收一部分爆炸压力，使得储罐在液位以上部分的变形大，液位以下部分的变形小，此种情况下储罐发生破坏时间介于空罐和满罐之间；对于满罐来说，由于爆炸冲击波在液体传播中受到的阻力随着液位的升高而增加，同时液体能吸收更多的爆炸压力，因此满罐时，储罐受到爆炸冲击波的影响比半罐和空罐时小，储罐不容易发生破坏。

对于不同TNT炸药当量，炸药当量为2 800 kg时，外罐和内罐没有发生破坏；而炸药当量为5 600，7 000，8 400 kg时，外罐和内罐都发生了破坏。炸药当量为7 000 kg和8 400 kg时，外罐发生破坏的时间分别比炸药当量为5 600 kg时缩短了3%和15.1%，内罐发生破坏的时间分别比炸药当量为5 600 kg缩短了5.3%和1.5%。外罐和内罐达到破坏时的应力都超过了屈服强度375 MPa，这是由于在爆炸载荷作用下，当应力超过材料的屈服强度时，储罐会出现不可恢复的塑性变形，随着冲击作用的加深，塑性应变会积累，当积累到一定程度后，材料就会发生破坏。

6 结论

(1)考虑外罐、保冷材料与内罐之间的载荷传递作用和罐内流体对外爆载荷的作用，建立了一个探究保冷材料不同状态和不同液位因素的空气-储罐结构-罐内流体多相耦合有限元模型，通过有限元计算方法得到了爆炸冲击波在不同介质中的传播规律以及储罐的固有频率、应力和变形等响应情况。

(2)爆炸冲击波到达外罐和内罐发生反射，使反射区域中的压力比该处自由空气中的爆炸压力大3倍左右；完整状态的保冷材料对爆炸冲击波形成了极大的阻力，保冷材料从完整至完全破碎过程中，爆炸反射压力逐渐降低，外罐和内罐变形增大、甚至会发生破坏。保冷材料完整时，爆炸反射压力数值达到了128.3 MPa，随着保冷材料逐渐发生破碎过程中，爆炸反射压力数值逐渐降低为95.9 MPa；在3 299 μs时，保冷材料完全破碎，此时外罐出现了破口，内罐的变形达到了1 490 mm，在3 749 μs时，内罐也开始出现破口。

(3)半罐和满罐时，内罐以及罐内流体达到压力峰值的时间都比空罐时延迟，压力峰值都比空罐时有所降低，流体的存在使外罐和内罐对爆炸冲击波抵抗能力提高。其中，半罐和满罐时，内罐达到压力峰值的时间分别比空罐时延后9.7%和12.8%，压力峰值分别比空罐时减小了29%和95.9%；半罐和满罐时，罐内流体达到压力峰值的时间分别比空罐时延后15.5%和61.7%，压力峰值分别比空罐时减小了26%和73.2%。半罐和满罐时，外罐对爆炸冲击波抵抗能力都比空罐时提高了至少一倍，而半罐和满罐时，内罐对爆炸冲击波抵抗能力比空罐时分别提高了20%和85%左右。