基于DIC的304奥氏体不锈钢裂纹尖端塑性区研究
代 巧,张 健,何爵亨,包骐乐,赵艳芳
(1.江苏理工学院 机械工程学院,江苏常州 213001;2.常州大学 江苏省绿色过程装备重点实验室,江苏常州 213164)
0 引言
压力容器通常承受交变载荷作用[1],疲劳断裂是其常见的失效形式,疲劳寿命预测能够为压力容器的安全运行提供保障[2-4]。疲劳失效通常要经历裂纹萌生、裂纹扩展、瞬时断裂三个阶段,其中疲劳裂纹扩展在整个寿命周期内占有一定比例,因此疲劳裂纹扩展行为研究对结构的疲劳寿命预测具有重要意义。在循环载荷作用下,裂纹尖端区域由于应力集中,材料将产生塑性变形,形成一定范围的塑性区。塑性区的形状、尺寸、应力及循环应力-应变关系对疲劳裂纹的扩展有着重要影响。IRWIN[5]通过对裂纹尖端塑性区内应力的研究,结合von Mises屈服准则给出了裂纹尖端塑性区的边界和尺寸计算。RICE[6]在文献[5]的基础上,提出了“塑性叠加理论”,给出了循环载荷下裂纹尖端小范围屈服的应力-应变场。石凯凯等[7]基于裂纹尖端的小范围屈服应力-应变场,得到裂纹尖端循环塑性区应力、应变分布,建立了疲劳裂纹扩展速率预测模型。因此,对疲劳裂纹尖端塑性区进行理论分析、试验研究,获取裂纹尖端应力-应变状态,分析裂纹尖端塑性区应变场随裂纹扩展的变化规律,对疲劳裂纹扩展行为研究具有重要的意义。
裂纹尖端应力-应变场主要通过理论分析来获得,一般试验方法很难精确获得,数字图像相关(Digital image correlation,DIC)技术的出现正好解决这一问题。DIC技术是一种光测力学变形的测量技术,通过图像匹配的方法分析物体表面变形前后的散斑图,跟踪散斑图上几何点的运动获得位移场,进而得到应变场,该技术已被广泛用于裂纹问题的研究。LOPEZ-CRESPO等[8]通过DIC技术获取了不同载荷条件下复合型裂纹的裂纹尖端应变场;CASPERSON等[9]基于DIC技术研究了热过载对高温镍基合金的疲劳裂纹闭合的影响;RABBOLINI等[10]利用DIC技术研究了高温镍基合金Haynes 230的疲劳裂纹扩展,获取其各向异性应力强度因子,采用各向异性屈服准则判定裂纹尖端反向塑性区范围,对裂纹尖端进行塑性分析。
本文以压力容器常用材料304奥氏体不锈钢为研究对象,考虑多个峰值载荷对其进行疲劳裂纹扩展试验,通过DIC技术获取裂纹尖端应变场;结合理论分析,对裂纹尖端区域进行划分,计算循环塑性区与单调塑性区尺寸,获取裂纹尖端循环应变范围及循环应力范围,以建立裂纹尖端塑性区内循环应力-应变关系。
1 疲劳裂纹扩展试验
1.1 试验材料与设备
试验材料为热轧304奥氏体不锈钢板,采用线切割加工为标准紧凑拉伸(Compact Tensile,CT)试样,试样宽度25 mm,缺口长度8 mm,引伸计缺口宽度5 mm,试样结构尺寸如图1(a)所示。疲劳裂纹扩展试验在MTS 810试验机上进行,采用引伸计记录裂纹张开位移数据,同时采用DIC技术对裂纹尖端应变场进行测量,检测装置如图1(b)所示。为了获得精确的裂纹尖端应变场,需在试样表面进行喷漆处理:首先将试样表面进行打磨抛光,使其满足精度要求,再喷白漆形成白底,待白漆干结后喷黑漆,形成对比散斑。试验开始前,试样1通过夹具2安装在疲劳试验机3上,试样的左侧为散斑面,通过相机支架4在散斑面一侧安装高清摄像头5,在摄像头与试样之间设有光源6,摄像头与计算机连接,其安装了德国GOM Correlate Professional软件,用于DIC测量数据采集和后处理分析。

(a)CT试样结构尺寸

(b)疲劳裂纹扩展试验平台
1.2 试验过程
根据GB/T 6398—2017《金属材料 疲劳试验 疲劳裂纹扩展方法》[11]对CT试样展开疲劳裂纹扩展试验,由引伸计记录裂纹张开位移,再由柔度法计算裂纹长度,同时,试验过程中采用DIC技术测量裂纹尖端应变场。在疲劳裂纹扩展试验前对各试样进行初始裂纹预制,载荷比为0.1,加载频率为10 Hz,预制初始裂纹长度为9.5 mm。疲劳裂纹扩展试验过程中采用恒幅载荷的增K试验(K为应力强度因子)[11],载荷比为0.1,加载频率为5 Hz,考虑多个载荷峰值以分析304奥氏体不锈钢疲劳裂纹尖端应力-应变情况,试验载荷峰值Pmax分别为2.2,2.5,3.0,3.5,4.0 kN。
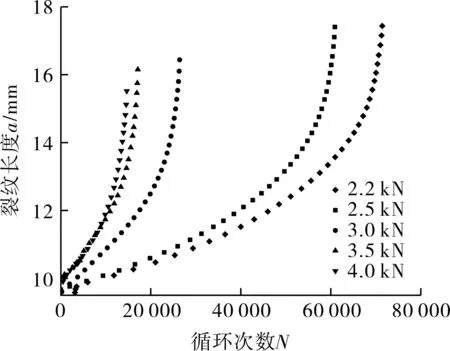
图2 304奥氏体不锈钢a-N曲线
疲劳裂纹扩展试验过程中,通过柔度法获得不同循环载荷条件下的裂纹长度a与循环次数N的关系曲线,如图2所示。可以看出,各循环载荷下均有明显的稳态裂纹扩展阶段,载荷越大,相同裂纹长度所对应的裂纹扩展速率越大。
2 304奥氏体不锈钢疲劳裂纹尖端应力-应变场
2.1 304奥氏体不锈钢疲劳裂纹尖端应变场
在304奥氏体不锈钢的疲劳裂纹扩展试验过程中,采用DIC方法对裂纹尖端应变场进行观测,获得了不同循环载荷作用下裂纹尖端应变场。由图2可以看出,各循环载荷下裂纹长度为13 mm时,疲劳裂纹扩展均处于稳态扩展阶段,取此时的应变场进行分析,以研究循环载荷大小对裂纹尖端应变场的影响,如图3所示(图中的应变云图为最大循环载荷时的von Mises等效应变场)。从图3可以看出,由于应力集中,裂纹尖端有最大应变值,且最大应变值随循环载荷的增加而增大;在裂纹尖端附近,材料产生了显著的塑性变形,应变值相对较大,随离裂纹尖端距离的增加,应变值不断减小;同时循环载荷越大,裂纹尖端塑性区域越大,应变场呈蝴蝶状越显著。


图3 a=13 mm时,不同循环载荷下裂纹尖端应变场
2.2 304奥氏体不锈钢裂纹尖端塑性区应力-应变行为
2.2.1 裂纹尖端塑性区
循环载荷作用下,裂纹尖端由于应力集中产生一定范围的塑性变形区域,基于变形行为的差异,裂纹尖端塑性区分为循环塑性区和单调塑性区[6],如图3(f)所示。在循环塑性区内,应变值远大于其他区域,材料产生可测量的塑性变形,随着循环载荷的作用,材料不断经历拉伸加载、拉伸屈服、弹性卸载及压缩屈服,应力-应变形成封闭的滞回曲线,循环塑性区尺寸rc可表示为[6]:
(1)
式中,ΔK为应力强度因子范围;nc为循环应变硬化指数;σy为循环屈服强度。其中,对于标准试样的应力强度因子可参考GB/T 6398—2017进行计算,循环应变硬化指数和循环屈服强度可由疲劳试验获得的循环应力-应变关系来确定。
材料的循环应变-应力关系由指数关系表示为[12]:
(2)
式中,Δε为应变范围;Δσ为应力范围;E为弹性模量;Kc为循环应变强度系数。
基于RICE[6]提出的塑性叠加法,根据含裂纹结构特征、加载条件、材料循环特性等参数,即可计算循环载荷下裂纹尖端小范围屈服的循环应力-应变场。循环载荷作用下,载荷从谷值单调上升至峰值产生的应变增量即应变范围Δε,对应的应力增量即应力范围Δσ,在裂纹尖端循环塑性区内,由于塑性变形显著,塑性应变范围远大于弹性应变范围,于是忽略弹性应变范围,离裂纹尖端距离r处的塑性应变范围和应力范围可表示为[12]:
(3)
在循环塑性区之外的单调塑性区内,应变值相对较小,材料产生的塑性变形较小,循环载荷作用下,该区域内仅有拉伸加载、拉伸屈服和弹性卸载,并无压缩屈服过程,单调塑性区尺寸由最大应力强度因子Kmax确定为[13]:
(4)
结合理论计算的裂纹尖端单调塑性区和循环塑性区尺寸,对DIC获得的裂纹尖端应变场进行区域划分,具体方法如下:首先根据载荷大小、裂纹长度及材料参数,通过式(1)(4)计算出裂纹尖端单调塑性区和循环塑性区的半径,得到以裂纹尖端为中心的单调塑性区和循环塑性区理论范围,此范围为圆形;然后选取DIC试验得到的蝴蝶样等效应变云纹中与理论范围的圆形相切线,确定单调塑性区和循环塑性区的蝴蝶样范围,即可实现载荷为4 kN、裂纹长度13 mm时的裂纹尖端区域划分,如图3(f)所示。
2.2.2 裂纹尖端循环应变范围
采用理论计算和试验分析两种方法分别获取304奥氏体不锈钢CT试样裂纹尖端的循环应变范围。首先根据RICE[6]给出的循环载荷下裂纹尖端小范围屈服应力-应变场,结合304奥氏体不锈钢的循环应力-应变行为,计算不同裂纹长度时裂纹尖端的应变范围理论值。通过拉伸试验和低周疲劳试验获得的304奥氏体不锈钢相关材料性能参数如表1[14]所示。

表1 304奥氏体不锈钢材料性能参数
首先,根据裂纹尖端循环塑性区尺寸与单调塑性区尺寸计算公式(见式(1)(3)),结合304奥氏体不锈钢的循环应力-应变行为,计算出不同循环载荷下,裂纹尖端循环塑性区及单调塑性区尺寸随裂纹长度的变化,如表2,3所示。

表2 疲劳裂纹尖端循环塑性区尺寸rc

表3 疲劳裂纹尖端单调塑性区尺寸rm
其次,根据RICE[6]给出的循环载荷下裂纹尖端小范围屈服应力-应变场可知,裂纹尖端塑性应变范围主要受ΔK影响,并与循环载荷、裂纹长度有关。结合式(1)与式(3),裂纹尖端塑性应变范围可表示为:
(5)
根据式(5)可知,当离裂纹尖端距离r与循环塑性区尺寸rc比值相同时,不同循环载荷下的裂纹尖端循环应变范围相同。由此计算获得的304奥氏体不锈钢疲劳裂纹尖端应变范围理论值如图4所示。

图4 循环应变范围随r/rc的变化
应变范围的试验获取可由DIC来实现,裂纹尖端某点处,一个循环内载荷峰值的应变与载荷谷值的应变相减,即可确定该点的循环应变范围。在第2.1节中通过DIC技术已经获得了304奥氏体不锈钢疲劳裂纹扩展过程中的裂纹尖端应变场,结合表2,3,确定对应的裂纹尖端塑性区大小,由此考虑应变范围的取值点。在裂纹尖端循环塑性区内,分别选取距裂纹尖端0.1rc,0.2rc,0.4rc,0.6rc,0.8rc,1.0rc处的特征点;在单调塑性区内,分别选取距裂纹尖端1.2rc,1.8rc,2.2rc,2.66rc处的特征点。通过各特征点在加载循环内的最大应变值与最小应变值,确定不同循环载荷下,各点的等效应变范围随裂纹扩展的变化,304奥氏体不锈钢疲劳裂纹尖端的应变范围理论值与DIC获得的试验值见图4。
从图4可以看出,基于理论公式和DIC分析得到的裂纹尖端塑性区内应变范围具有相同的变化趋势,最大应变范围位于裂纹尖端处,且应变范围随离裂纹尖端的距离增加而减小。当r/rc为0~1 时,该区域为裂纹尖端循环塑性区,在循环塑性区内,最小应变范围在循环塑性区边界处,且随着靠近裂纹尖端,应变范围快速增大。当r/rc为1~2.66时,该区域为单调塑性区,应变范围变化较小,最大应变范围在循环塑性区边界处,并沿着裂纹扩展方向缓慢减小并趋于有限值,在单调塑性区边界上,塑性应变为零,此时的应变范围等于弹性应变范围,因此应变范围沿裂纹扩展方向趋近的有限值为裂纹尖端塑性区中最小弹性应变范围。
此外,基于DIC分析获得的裂纹尖端塑性区内应变范围与理论值相比,当r/rc=0.1时,试验值均小于理论值,且载荷越小,裂纹长度越短,偏差越大;随着r/rc的增大,试验值与理论值的偏差减小,试验值分布于理论值的两侧。因此,基于DIC分析得到的裂纹尖端塑性区内应变范围具有较好的精度,展示了裂纹扩展过程中裂纹尖端塑性区内应变范围的变化规律。
2.2.3 裂纹尖端循环应力范围
根据获得的304奥氏体不锈钢疲劳裂纹尖端的循环应变范围,以及RICE[6]给出的循环载荷下裂纹尖端小范围屈服应力-应变场,即式(2),可计算出相应的应力范围,由此建立裂纹尖端的循环应力-应变关系。将裂纹尖端塑性区循环应力-塑性应变曲线、循环应力-应变曲线,与单轴拉伸应力-应变曲线及低周疲劳试验获得的循环应力-应变曲线[14]进行比较,如图5所示。
图5中给出的是应力幅Δσ/2与应变幅Δε/2的关系,可以看出,单调塑性区与循环塑性区的分界线为应变幅0.14%,在单调塑性区,应力幅值较小,对应的塑性应变幅较小;在循环塑性区内,随着靠近裂纹尖端,应力幅逐渐增大,塑性应变幅逐渐增大,并逐渐趋近于总应变幅。图中裂纹尖端循环应力-应变曲线与循环应力-塑性应变曲线之间形成的间隙代表了裂纹尖端塑性区的弹性应变幅,在单调塑性区内,弹性应变幅大于塑性应变幅,当总应变幅为0.14%,即在循环塑性区与单调塑性区边界处,弹性应变幅与塑性应变幅相当,之后塑性应变幅快速增大,并占主导地位。

图5 304奥氏体不锈钢疲劳裂纹尖端循环应力-应变关系曲线
3 结论
本文对304奥氏体不锈钢进行疲劳裂纹扩展试验,采用DIC技术对裂纹尖端应变场进行观测,并结合塑性叠加法对裂纹尖端塑性区进行划分,获取裂纹尖端的循环应力-应变关系,得到主要结论如下。
(1)基于DIC获得的裂纹尖端应变场分析发现,裂纹尖端有最大应变值,且最大应变值随循环载荷的增加而增大;同时,循环载荷越大,裂纹尖端塑性区域越大,应变场呈蝴蝶状越显著。
(2)基于理论公式计算裂纹尖端应变范围,当离裂纹尖端距离r与循环塑性区尺寸rc比值相同时,裂纹尖端应变范围的理论值相同,而DIC结果与循环载荷相关;同时,随离裂尖距离的增加,裂纹尖端应变范围的理论值、DIC结果具有相同的变化趋势,裂纹尖端塑性区内最大应变范围在裂纹尖端处,随着远离裂纹尖端应变范围减小。
(3)结合塑性叠加理论,根据DIC获得的裂纹尖端循环应变范围计算相应的循环应力范围,以此建立了裂纹尖端的循环应力-应变关系,循环塑性区内塑性应变占主导地位。

