小弹目速度比下拦截高超声速飞行器微分对策制导律研究

刘双喜，王一冲，朱梦杰，李 勇，闫斌斌

（1.西北工业大学无人系统技术研究院，陕西西安 710072；2.上海机电工程研究所，上海 201109；3.西北工业大学航天学院，陕西西安 710072）

0 引 言

随着空天技术的不断发展，世界各国之间的军事竞争范围逐渐扩大到外层空间。高超声速飞行器凭借其攻击速度快、飞行距离远、可多平台发射、具备一定的机动能力等特点，可以对各类军事目标实现远程快速打击，极大地增加突防和摧毁目标的概率，完成常规导弹无法完成的任务，这给现有的防空反导防御系统带来了严峻的挑战。

比例导引律（proportional navigation guidance，PNG）因其形式简单、易于实现，而被广泛应用。杨佳等采用高抛弹道拦截的设计思路，将拦截弹抛射到较高的空域，采用修正比例导引法实现对高超声速飞行器的拦截任务。于志鹏等基于末角约束比例导引法，设计出空基拦截弹复合制导律，充分利用拦截弹中制导段过载承受能力，有效地加快了拦截弹达到期望末视线角的速度，能够对典型机动目标实施有效拦截。邵节等在扩展比例导引律的基础上，采用模糊逻辑理论，使导弹在拦截过程中能够有效地跟踪弹目视线角速率的变化及目标的机动加速度，实现高效拦截。张佳梁等基于非线性反演方法，在制导律设计中引入已知的控制回路时间常数信息，并对有效导航比系数进行修正。周觐等针对高超声速飞行器拦截问题，通过分析拦截弹速度前置角和目标速度前置角的变化关系，给出了真比例导律下拦截弹可拦截区域数值计算结果。然而，PNG 及以其为基础的改进型制导律对静止或匀速目标的制导效果较好，对于高速、大机动目标，则需要准确的目标加速度信息，而不准确的目标加速度信息会对制导效果产生极大影响，因而适用范围受到了一定的限制。

近年来，随着现代控制理论和非线性控制理论的兴起，基于滑模理论的制导律也在高超声速飞行器拦截中得到广泛的应用。Liu 等基于零化视线角速率方法，将分数阶算子引入滑模面中，设计了一种小弹目速度比下拦截高超声速飞行器的分数阶滑模制导律，实现对高超声速飞行器的高精度拦截。Chen等采用高阶滑模观测器对目标机动信息进行估计，并结合虚拟控制思想，提出针对高超声速飞行器制导控制一体化的方法。为了减小弹目相对运动速度并且降低对拦截弹的过载能力要求，司玉洁等采用连续快速双幂次趋近律，提出有限时间收敛的三维前向拦截自适应滑模制导律。杨峰将高超声速飞行器的拦截问题转化为视线角速率（或视法向速度）的有限时间鲁棒控制问题，采用通用super-twisting 算法进行了三维制导律设计。然而，在设计基于滑模理论的制导律过程中，大多数情况需要假设目标机动形式已知，对目标加速度信息依赖性强，导致制导参数选取比较困难，且在制导末端容易发生抖振现象，亦没有考虑最优特性来保证导弹能够在中远程距离执行任务。

微分对策制导律对于精确目标加速度信息的依赖程度较小，制导过程中只需要目标的机动能力信息，而不需要精确的目标加速度信息。微分对策理论，是一种双边最优理论，即考虑“追-逃”双方的最优策略。如果“追-逃”双方有一方不动，而只把另一方按照某个代价函数的最小或最大带到目标位置，则称为最优控制；如果双方都在运动，且一方要求目标函数最小，另一方要求目标函数最大，那么两方如何运动的对策问题就称为微分对策理论。微分对策理论不断地被应用到很多军事背景问题中，比如目标的拦截、对拦截的规避、军事策略的制定等。Shima基于线性时变微分对策追逃模型，推导用于拦截弹道导弹的微分对策制导律，并详细分析了能够实现零脱靶量的条件。Shinar在设计微分对策制导律的过程中，对制导信息的延迟进行了研究，并通过仿真实验证明了其在制导信息延迟环境仍然具有稳定的跟踪效果。花文华等通过选取合适的状态变量对速度可控导弹模型进行合理线性化，推导出微分对策制导律形式，对带有攻击角约束的情形进行了微分对策问题的指标设计，还通过系统的降阶实现了解析形式的制导律求解。孙磊等针对具有主动博弈突防能力的高超声速目标拦截场景，采用基于双启发式的自适应动态规划算法，对连续非线性系统的微分对策纳什均衡解进行求取来设计相应的制导律。许佳骆等针对延迟信息条件下的机动目标拦截问题，设计出一种考虑目标加速度方向观测的微分对策制导律。

本文针对高超声速飞行器速度快、机动能力强的特点，基于微分对策理论，利用状态依赖黎卡提方程（state-dependent Riccati equation，SDRE）方法研究了小弹目速度比下高超声速飞行器拦截问题，将高超声速飞行器拦截问题转化为状态依赖参数（state-dependent coefficient，SDC）和代数黎卡提方程的求解，给出了基于状态依赖黎卡提方程方法微分对策制导律（SDRE-DG）。通过对比比例制导律和自适应滑模制导律，证明了所设计的微分对策制导律在小弹目速度比下拦截高超声速飞行器的可行性及优越性。

1 问题描述

为了准确地分析微分对策问题，对拦截制导律进行求解，需要对拦截弹与高超声速飞行器的相对运动关系进行建模分析。末制导阶段纵向平面内弹目相对运动关系如图1所示。

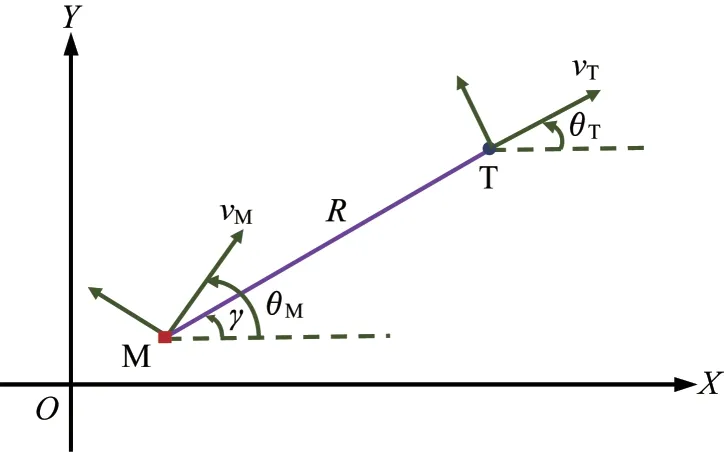
图1 纵向平面内弹目运动关系Fig.1 Relative motion in the longitudinal plane

图1中，拦截弹用M表示，高超声速飞行器用T表示。表示惯性坐标系，表示弹目相对距离，表示弹目视线角。、、分别表示拦截弹的速度、弹道倾角和法向加速度；、、分别表示高超声速飞行器的速度、弹道倾角和法向加速度。

拦截弹的运动学模型可表达为

本文基于“零化视线角速率”的方法，设计微分对策制导律对高超声速飞行器实施精准打击。因此，本文的制导律设计任务可以归纳为：基于微分对策理论，设计合理的制导指令使liṁ=0（其中，表示拦截时刻时间）。

2 微分对策制导律设计

2.1 制导律性能指标设计

由式（4）可知，影响拦截弹制导精度的因素只和̇有 关。因 此，选 取 状 态 变 量∈R，令=̇，针 对式（4），建立拦截弹和高超声速飞行器的微分方程，可表示为

式中：>0表示高超声速飞行器相对于拦截弹的机动能力大小，值越大，表示高超声速飞行器机动能力越小；() 表示与视线角速率相关的权重系数；()和()分别表示和拦截弹与高超声速飞行器机动指令相关的权重系数。

由式（7）可知，对于拦截弹M，应该选择最佳指令，使得性能指标函数取得最小值；而对于高超声速飞行器T，应选择最佳指令，使性能指标函数取得最大值。

2.2 SDRE-DG制导律求解

目前，求解微分对策最常用方法是梯度迭代法，然而该方法计算工作复杂，并且会遇到难以求解的两点边值的问题，严重影响制导律计算的快速性和有效性。SDRE方法是一种基于状态反馈的非线性控制方法，其基本思想是将非线性系统方程通过系统状态相关的矩阵伪线性化得到线性二次型调节器（linear quadratic regulator，LQR）方法类似控制器形式并求解得到其解析解。本文采用SDRE方法对微分对策制导律进行求解，可以将高超声速飞行器拦截问题转化为SDC和代数黎卡提方程的求解，这样不仅可以满足计算的快速性和性能指标的要求，还可以舍去黎卡提方程的微分项以避免在制导指令中出现剩余时间估计。

对于式（5），假设()=0，则()可以表示为()=()。那么，式（5）就转化为所需要的SDC形式，可表示为

观察可知，上式制导律中不需要计算拦截弹剩余飞行时间，并且在制导律计算过程中综合考虑了拦截弹和目标之间的运动，充分体现了拦截弹和目标之间的博弈对抗关系。制导律中包含了目标的机动能力，并且不需要提前知道目标具体的机动形式，具有一定的工程实现价值。

3 仿真分析

基于SDRE-DG 的微分对策制导律仿真框图如图2所示。

图2 制导律仿真框图Fig.2 Block diagram of the proposed guidance law simulation

为了对本文所设计的微分对策制导律的可行性进行分析，假设仿真环境是理想条件，即：，，是可以实时精准测量的；，，̇是可以实时精准预测的。拦截弹和高超声速飞行器的仿真初始条件如表1所示。

表1 仿真初始条件Tab.1 Initial conditions of simulation

此外，为了验证SDRE-DG 微分对策制导律算法的优越性，将比例导引律PNG和文献［23］中自适应滑模制导律（adaptive sliding-mode guidance，ASMG）的仿真结果作为参考，进行对比分析。分别针对高超声速飞行器不机动、进行常值机动及不同弹目速度比3种不同拦截场景开展实验。拦截弹的最大法向过载为12，各制导律下的拦截弹法向过载表达为

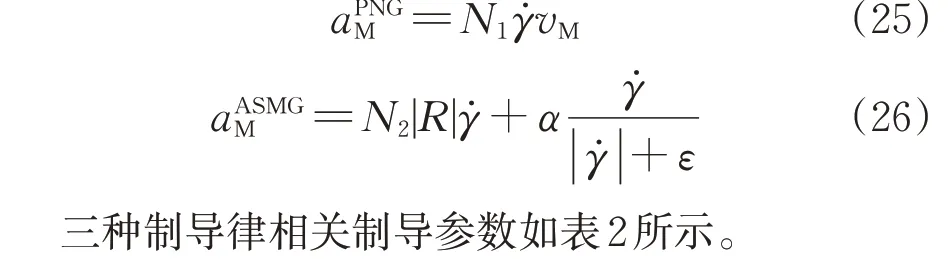
表2 制导律参数Tab.2 Guidance parameters

3.1 高超声速飞行器不机动情况

当高超声速飞行器不机动时，3 种制导律的仿真结果如表3和图3所示。

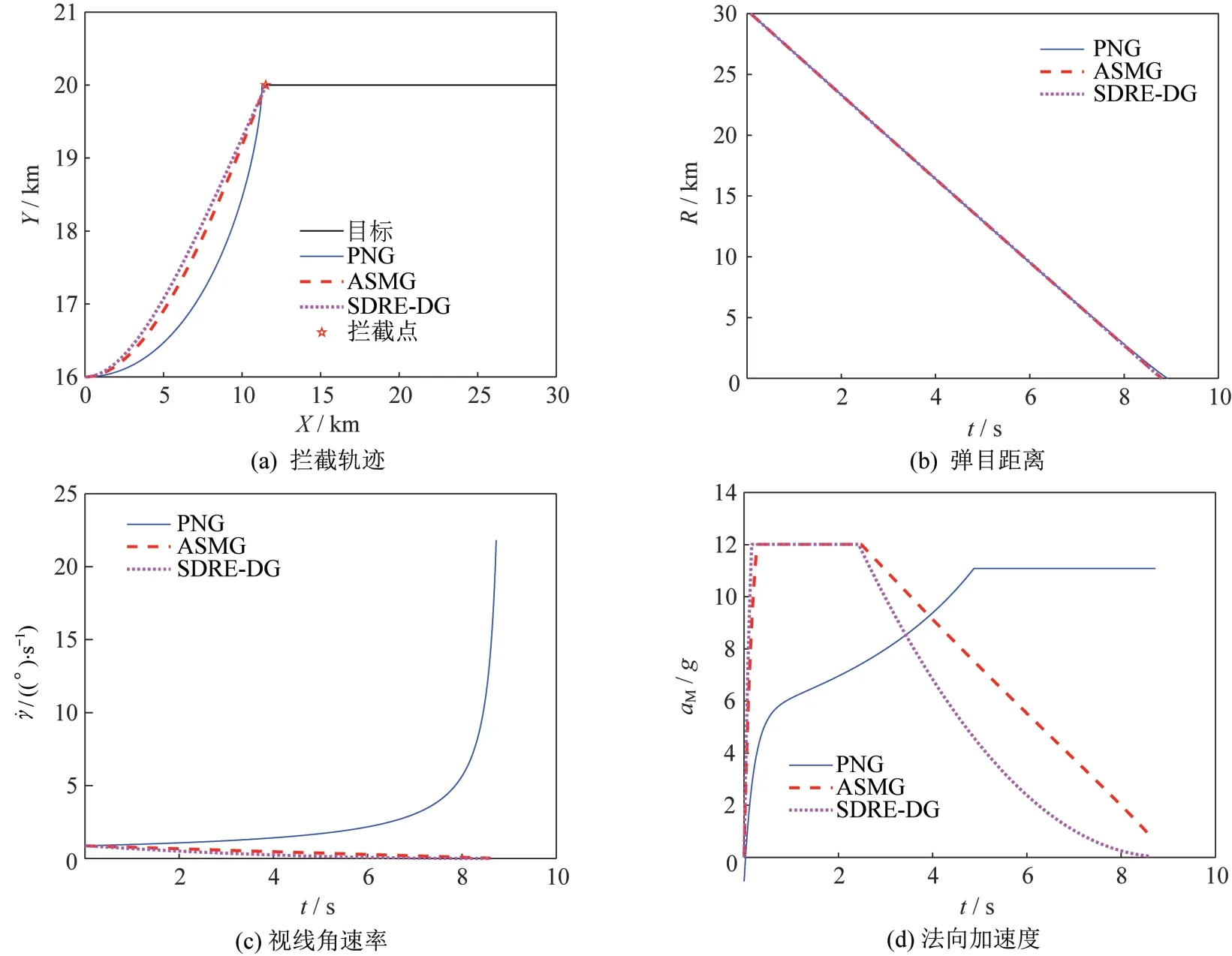
图3 高超声速飞行器不机动时仿真结果Fig.3 Simulation results when hypersonic vehicle is not maneuvering

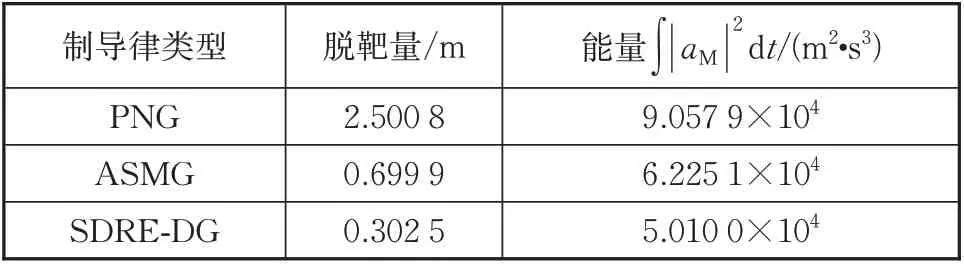
表3 高超声速飞行器不机动时分析结果Tab.3 Analysis results when hypersonic vehicle is not maneuvering

由仿真结果可知，采用PNG时脱靶量最大，并且视线角速率随着制导时间的增大逐渐呈现出发散的趋势。由于比例导引律的制导指令和视线角速率成正比关系，导致拦截器的需用过载随着制导时间的增加而增大，这样的过载分布对于拦截器来说具有很大的缺陷。采用ASMG和SDRE-DG两种制导律时，拦截弹均能成功拦截目标，脱靶量分别为0.699 9 m和0.302 5 m，并且在拦截时刻视线角速率均趋于0，符合制导律设计任务要求。但采用SDRE-DG的拦截弹道相对于ASMG的拦截弹道更加平直，所消耗的能量最小，并且视线角速率和法向加速度的收敛速度略胜一筹。

3.2 高超声速飞行器机动

假设高超声速飞行器法向加速度变化规律为2sin(π/3+π/4)，3种制导律的仿真结果如表4和图4所示。

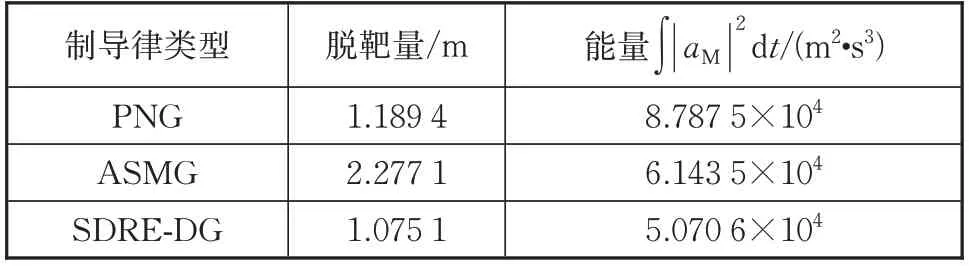
表4 高超声速飞行器常值机动时分析结果Tab.4 Analysis results when hypersonic vehicle is maneuvering

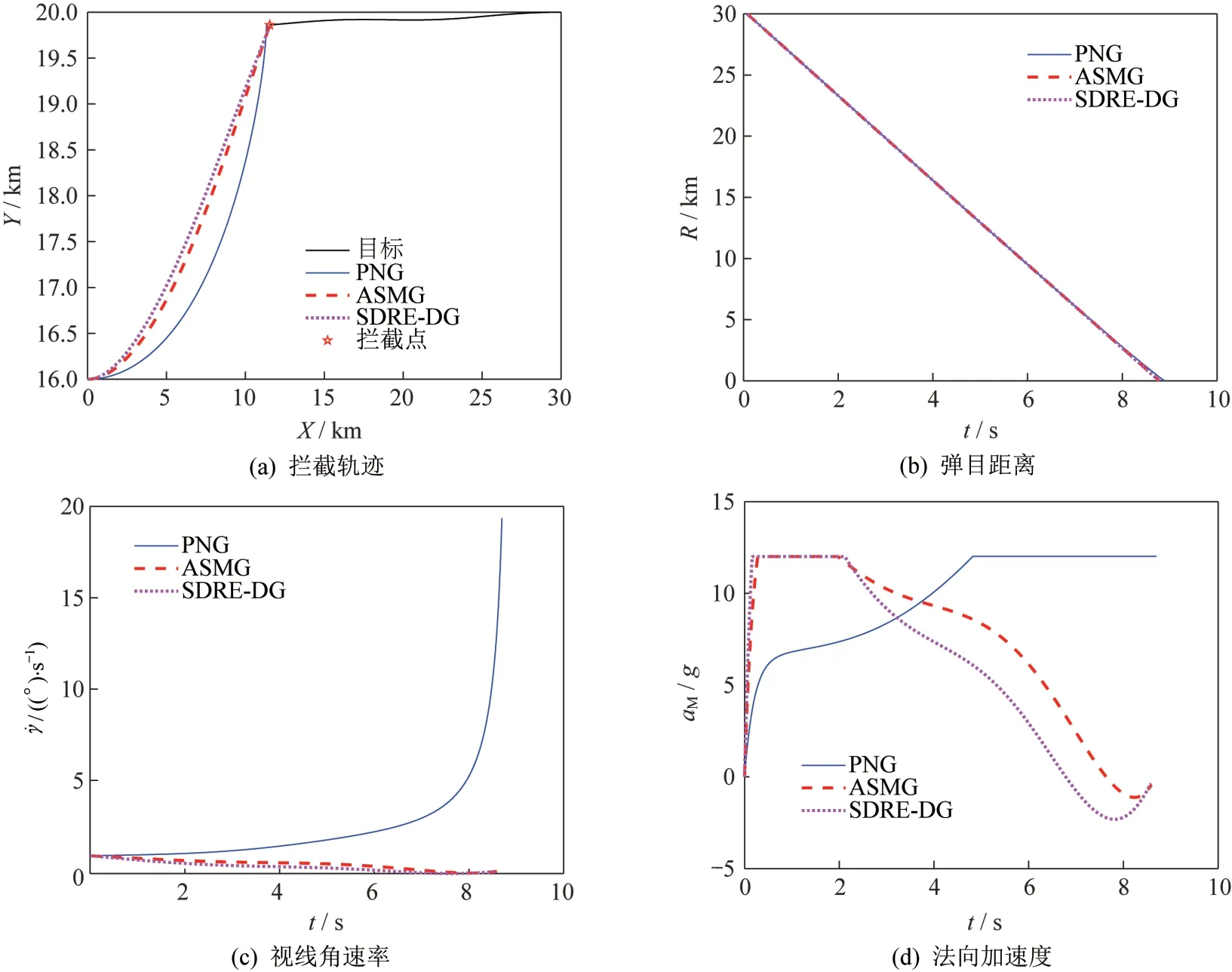
图4 高超声速飞行器常值机动时仿真结果Fig.4 Simulation results when hypersonic vehicle is maneuvering

由仿真结果可知，拦截弹在3 种制导律的导引下均可成功拦截目标。采用SDRE-DG 时，拦截精度最高，所消耗的能量最少，并且在视线角速率和法向加速度收敛方面的优势更为明显，拦截弹道更加平直。

3.3 不同弹目速度比

从前面的分析可以看出，SDRE-DG具有拦截精度高、末端过载小、弹道平直等优势。定义=：，表示弹目（拦截弹和高超声速飞行器）速度比，分别分析5种不同弹目速度比下，PNG和SDRE-DG两种制导律的制导性能，拦截弹和高超声速飞行器的仿真初值与3.1节一样，仿真结果如表5及图5～6所示。

表5 不同弹目速度比下仿真分析Tab.5 Simulation analysis of the different missile-to-target speed ratios

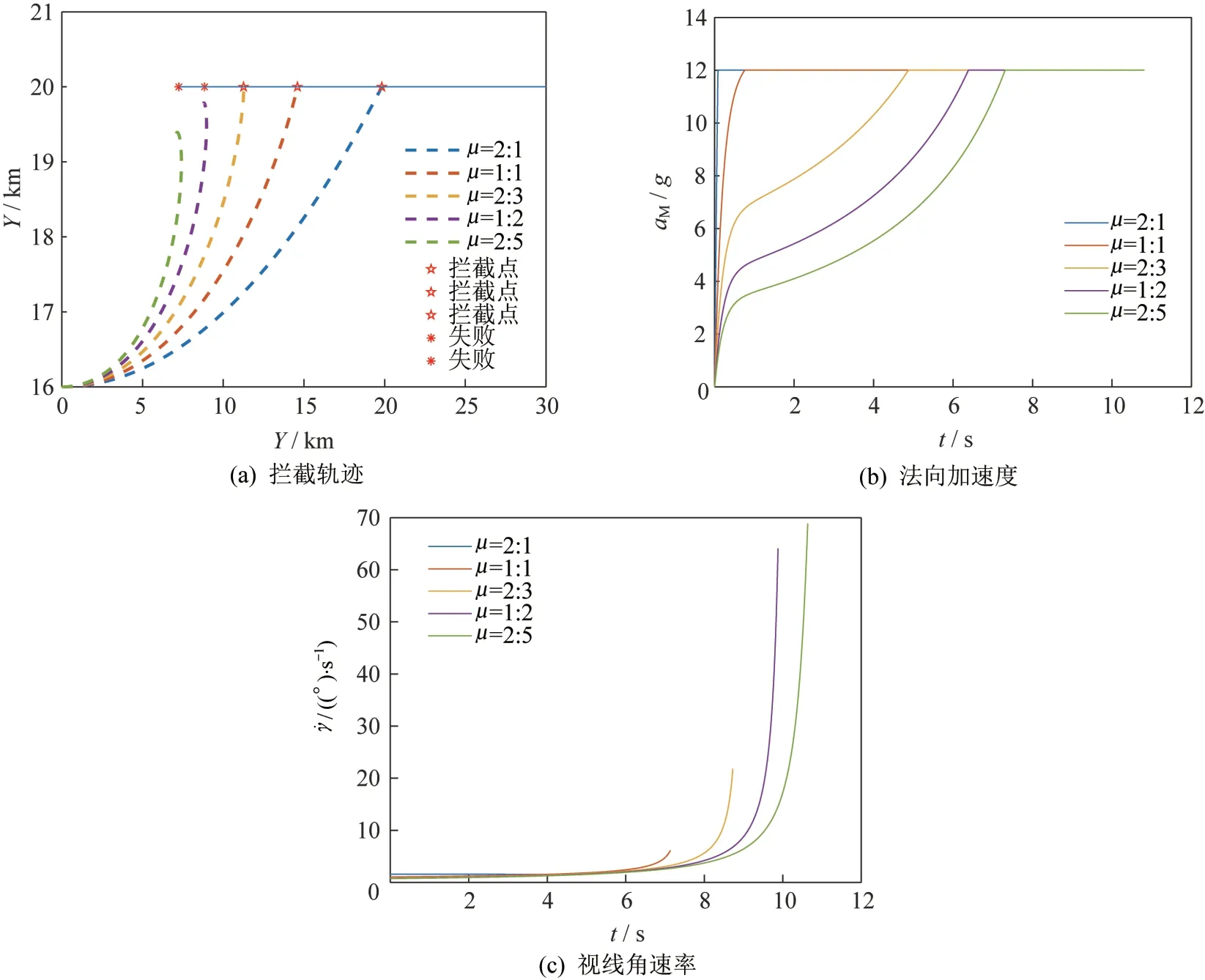
图5 不同弹目速度比下仿真结果（PNG）Fig.5 Simulation results of the different missile-to-target speed ratios（PNG）

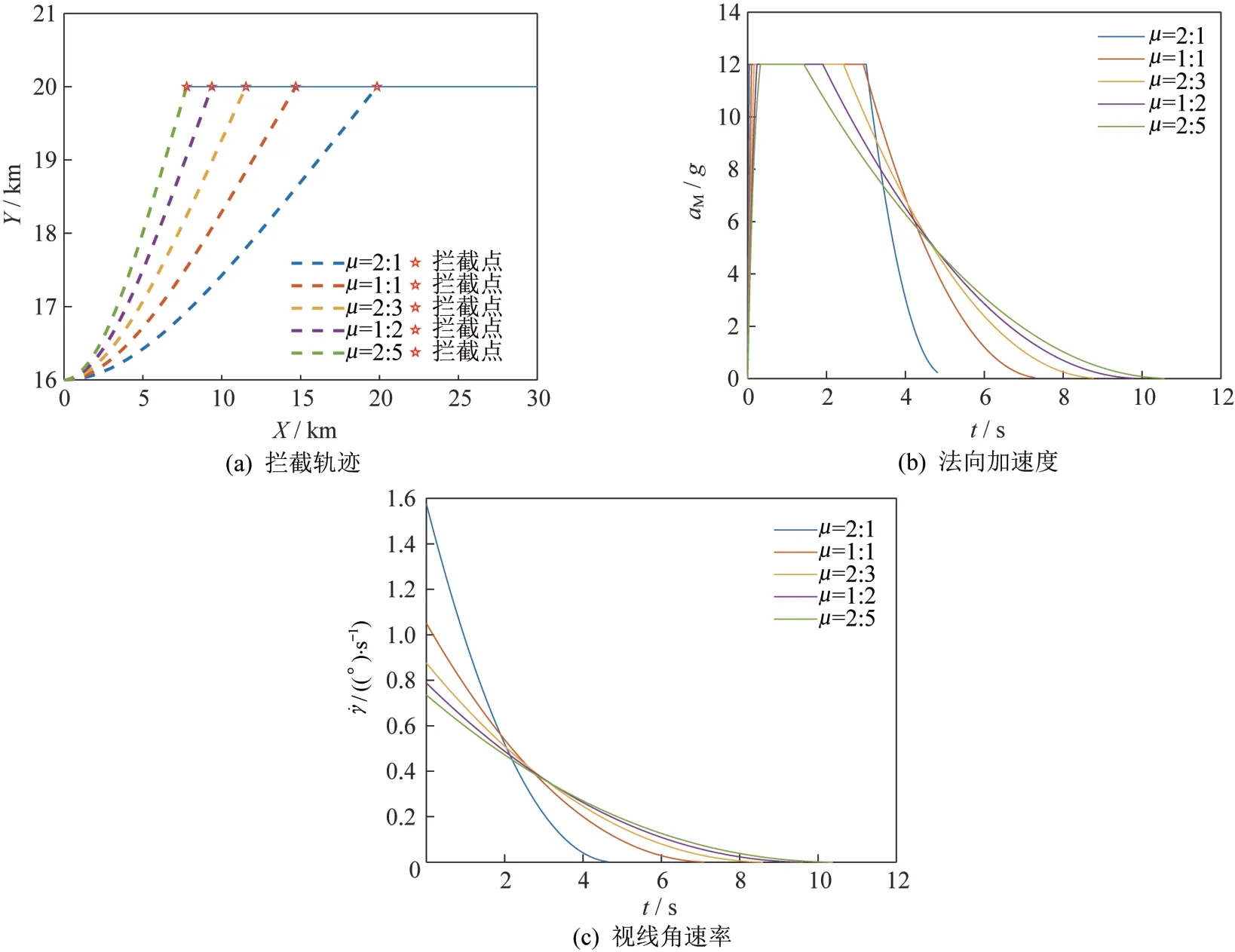
图6 不同弹目速度比下仿真结果（SDRE-DG）Fig.6 Simulation results of the different missile-to-target speed ratios（SDRE-DG）

由仿真结果可知，当弹目速度比小于（2∶3）时，PNG 无法满足拦截任务需求，而SDRE-DG 在不同弹目速度比下均可成功拦截目标，且同等条件下的制导精度和消耗能量均优于PNG，在小弹目速度比下具有较好的拦截效果。法向加速度分布方面，采用PNG时，随着弹目速度比的减小，法向过载的饱和时间在逐渐后移；采用SDRE-DG 时，随着弹目速度比的减小，法向过载在制导初期的饱和时间也逐渐减小，并且在拦截时刻趋于0。视线角速率分布方面，视线角速率随着弹目速度比的减小而逐渐增大，呈现出发散的趋势，由于PNG 和视线角速率成正比关系，导致制导精度逐渐降低；采用SDRE-DG 制导律可以保证拦截弹在不同弹目速度比下的视线角速率在拦截时刻趋于0，在保证了制导精度的同时也满足了制导任务需求。

4 结束语

本文针对高超声速飞行器拦截问题，设计了小弹目速度比下拦截高超声速飞行器微分对策制导律。该制导律选取拦截弹与高超声速飞行器视线角速率为状态量进行推导，给出了基于状态依赖黎卡提方程方法微分对策制导律（SDRE-DG）解析解形式，并针对高超声速飞行器不机动、进行常值机动及和不同弹目速度比下3种情况进行仿真验证。本文所设计的微分对策制导律具有对高超声速飞行器拦截精度高、机动不敏感及拦截末端需用过载小的特点，拦截性能优于比例制导律和自适应滑模制导律的拦截性能，在小弹目速度比下的拦截场景中更有优势。