DSets-DBSCAN无参数聚类的雷达信号分选算法
刘鲁涛,王璐璐,李 品,陈 涛
(1. 哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001; 2. 南京电子技术研究所, 江苏 南京 210000)
雷达信号分选是雷达信号处理中的重要一环,只有从多部随机交错的脉冲信号流中正确地分离出各单部雷达辐射源脉冲,才能对雷达数据进行准确分析,因此雷达信号分选的准确性直接影响了雷达的性能[1]。雷达信号分选主要由信号预分选和主分选两部分组成,信号预分选作为雷达信号分选的一部分,主要是利用到达角(direction of arrival, DOA)、载频(carrier frequency, CF)和脉宽(pulse width, PW)等参数进行聚类,对密集脉冲流进行稀释处理,初步实现信号去交错,便于主分选进行处理[2],所以能正确聚类是得到准确分选结果的前提。
现有预分选算法主要是在K均值(K-means)聚类算法[3-4]、模糊C均值聚类(fuzzyC-means, FCM)算法[5]、密度聚类[6-7](density-based spatial clustering of applications with noise, DBSCAN)等几个主流算法上进行改进,文献[8]将数据场与K-means相结合,解决了传统K-means聚类算法对初始聚类中心敏感问题;文献[9]采用可变FCM(alternative fuzzyC-means, AFCM)算法对对称聚类的参考点进行初始化,以改善噪声和错误排序的影响;文献[10]在DBSCAN基础上进行了改进,解决了DBSCAN算法不能分选密度分布不均雷达信号的缺陷。
尽管上述算法及其改进算法在很大程度上完成了对复杂环境下雷达脉冲信号的聚类,但是这些算法得到的聚类效果都依赖于参数或阈值的选取[9,11]。针对上述问题,本文将无参数DSets-DBSCAN聚类算法应用于雷达信号处理中,给出了一种无参数的雷达信号脉冲聚类算法,该算法无须依赖于任何参数的设置就能自动聚类。
DSets-DBSCAN结合了主导集(dominant sets, DSets)聚类算法[12]和DBSCAN两种算法。首先将雷达脉冲描述字(pulse descriptive word, PDW)参数形成的相似性矩阵经过图像增强技术(直方图均衡化)处理后输入DSets算法中,该过程不涉及任何参数,并且能够得到仅球形的脉冲超小簇。然后使用DBSCAN算法扩展刚生成的脉冲超小簇,尽管DBSCAN需要输入参数邻域半径Eps和邻域中的最小点数MinPts,但是能够根据DSets生成的超小簇自适应确定,且是以区域增长的方式生成任意形状的簇。通过这种方式,可以克服DSets的过度分割趋势,并生成任意形状的簇。由于DSets算法仅使用成对相似性矩阵作为输入,且DBSCAN的输入参数由DSets提取的脉冲集群确定,因此本文使用的DSets-DBSCAN算法不涉及任何参数。除此之外,这两种算法的结合可以有效地抑制噪声对脉冲聚类结果的影响。
1 算法流程
与DSets和DBSCAN一样,DSets-DBSCAN算法在聚类过程中按顺序提取脉冲集群。首先,输入由DOA、PW和CF形成的三维PDW数据,并进行相似性矩阵的生成;其次,将连续的空间进行离散化,得到的结果进行直方图均衡化,以此来消除参数σ对算法的影响;再次,处理后的相似性矩阵利用复制动力学因子求解一个聚类结果DSet;最后,利用DBSCAN算法扩展集群,输入参数由DSet确定,得到一个最终聚类结果,同时去除已聚类脉冲在相似性矩阵中对应的行和列,重新进行下一次聚类结果的提取。算法流程如图1所示。
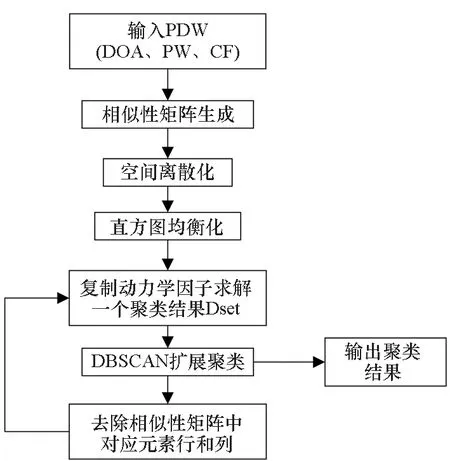
图1 算法流程Fig.1 Algorithm flow chart
2 数据预处理
2.1 相似性矩阵生成
假设接收到的脉冲数目为M,脉冲向量为(p1,p2,…,pM);pm=[cfm;pwm;doam],m=1,2,…,M,则各脉冲参数间的相似性度量构成的相似性矩阵如式(1)所示。
(1)

2.2 直方图均衡化
不同σ得到的相似性矩阵之间的差异主要在于相似性对比,这些差异与不同灰度对比度的图像之间的差异非常相似[9]。所以可以利用直方图均衡化使不同的σ生成相同的相似性矩阵,从而得到相同的聚类结果,消除算法对参数σ的依赖。
首先将一个连续空间变换成一个离散空间,将相似性矩阵离散化为N个灰度等级。离散化后的相似性矩阵记为A1=[s1(pi,pj)]M×M(i=1,2,…,M;j=1,2,…,M)。
由于s1(pi,pj)的相对大小只取决于元素之间的距离,与σ无关,且值均在[0,1]之间,所以可以直接通过式(2)完成直方图均衡化[13]:
(2)
其中:k=1,2,…,L-1,L是灰度级数;nj是灰度级j的像素数;n是所有像素数,直方图均衡化后的相似性矩阵记为Ahisteq。
但是,当一个灰度等级中包含一个以上元素时,相似度范围的离散化使得变换后的相似性矩阵略有不同,这就是直方图均衡化后的相似性矩阵仍然存在略微差异的原因。为了便于表达,本文在下面使用DSets-histeq表示直方图均衡化后的DSets聚类算法。
3 DSets-DBSCAN无参数聚类
3.1 DSets算法
DSets算法得到的每个主导集严格满足簇的高度内部相似性,一旦集合内部包含任何来自外部的数据,内部相似性将被破坏,这个条件使DSet成为数据的最大一致性子集。将直方图均衡化后的相似性矩阵Ahisteq输入DSets中,集群内部相干性的自然表示方法是f(x)=xTAhisteqx,其中xT表示的是x的转置,将聚类问题公式化为寻找使f最大化的向量x的问题[14]:
maxf(x) s.t.x∈Δ
(3)
其中,Δ={x∈Rn:∑ixi=1,xi≥0}为Rn的标准单纯形。 通过DSets的加权特征向量,证明了式(3)的严格局部解与DSet一一对应。
利用进化博弈论中发展起来的复制因子动力学求解式(3)并提取DSet,如式(4)所示:
(4)

3.2 DSets-DBSCAN算法
从主导集的定义[12]可知,主导集对主导集内的所有数据强加了全局密度约束。为了满足此条件,主导集中的每个脉冲数据必须与主导集中的所有其他脉冲成员非常相似。这种严格的条件会产生两个后果:①很难将同一部雷达的所有脉冲数据收集到同一个集合中,导致DSets聚类结果过小,出现将同一部雷达聚类为多部雷达的过度分割现象;②聚类仅形成球形的聚类结果,不能将任意形状的脉冲进行聚类。显然这两种后果都会损害雷达信号的聚类质量。
为了解决上述问题,给出了DSets-DBSCAN算法进行雷达信号脉冲聚类,该算法通过将DSets和DBSCAN这两个算法的互补性差异结合起来,得到分选性能更好的聚类算法。在使用DSets算法聚类之前,将直方图均衡化变换应用于相似性矩阵,所以DSets聚类步骤没有参数输入;然后使用DBSCAN[15]扩展主导集时,根据主导集确定DBSCAN所需的参数。这样确保在整个脉冲聚类过程中,不需要用户指定任何参数。此外,由于使用DBSCAN将主导集扩展为聚类,可以很好地解决过度分割问题,并可以获得任意形状的聚类结果。
与DBSCAN相比,DSets-DBSCAN受MinPts的影响较小,这将在仿真结果中显示。下面就是自适应地确定Eps参数,如式(5)所示:
(5)
其中,S是主导集,pMinPts是距离脉冲p最近的第MinPts个脉冲元素,p和pMinPts都在集合S中。对于每个脉冲集群,算法会根据相应的主导集为每个脉冲集群自适应地生成Eps,与原始DBSCAN中使用的全局参数不同。
MinPts和Eps两个参数确定完毕后使用DBSCAN算法扩展主导集:从主导集中的任意脉冲开始检索所有密度可达到的脉冲数据点,并获得一个聚类。从脉冲数据集中删除聚类的脉冲数据,重复进行主导集提取和扩展的过程,完成剩余脉冲聚类并自动确定聚类数。算法流程如下:
步骤1:输入包含CF、PW和DOA三个参数的脉冲向量(p1,p2,…,pM),利用式(1)计算相似性矩阵A。
步骤2:将相似性矩阵A进行离散化得到A1,应用直方图均衡化变换相似性矩阵A1,得到Ahisteq。
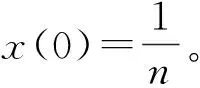
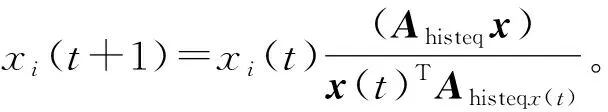
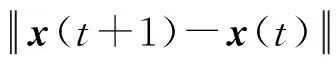
步骤6:设置MinPts=3并根据式(5)确定Eps;
步骤7:从S中的任意脉冲开始,检索所有密度可达的脉冲数据,形成一个聚类C。
步骤8:从相似性矩阵Ahisteq中删除与C中脉冲数据相关的行和列。
步骤9:转到步骤4,直到完成所有脉冲聚类。
4 实验结果与分析
为了验证算法的可行性,本节进行了软件仿真,通过对设定的雷达信号进行聚类,来测试算法的聚类效果。由于DSets-DBSCAN算法旨在融合DSets算法和DBSCAN算法的优点,因此本节将本算法与DSets-histeq和DBSCAN算法分别进行了比较,以此来测试本算法是否达到目标。除此之外,为了验证本文方法在高虚假脉冲比例下的聚类性能,给出了与现有方法的仿真结果对比图。数据形式如表1所示。
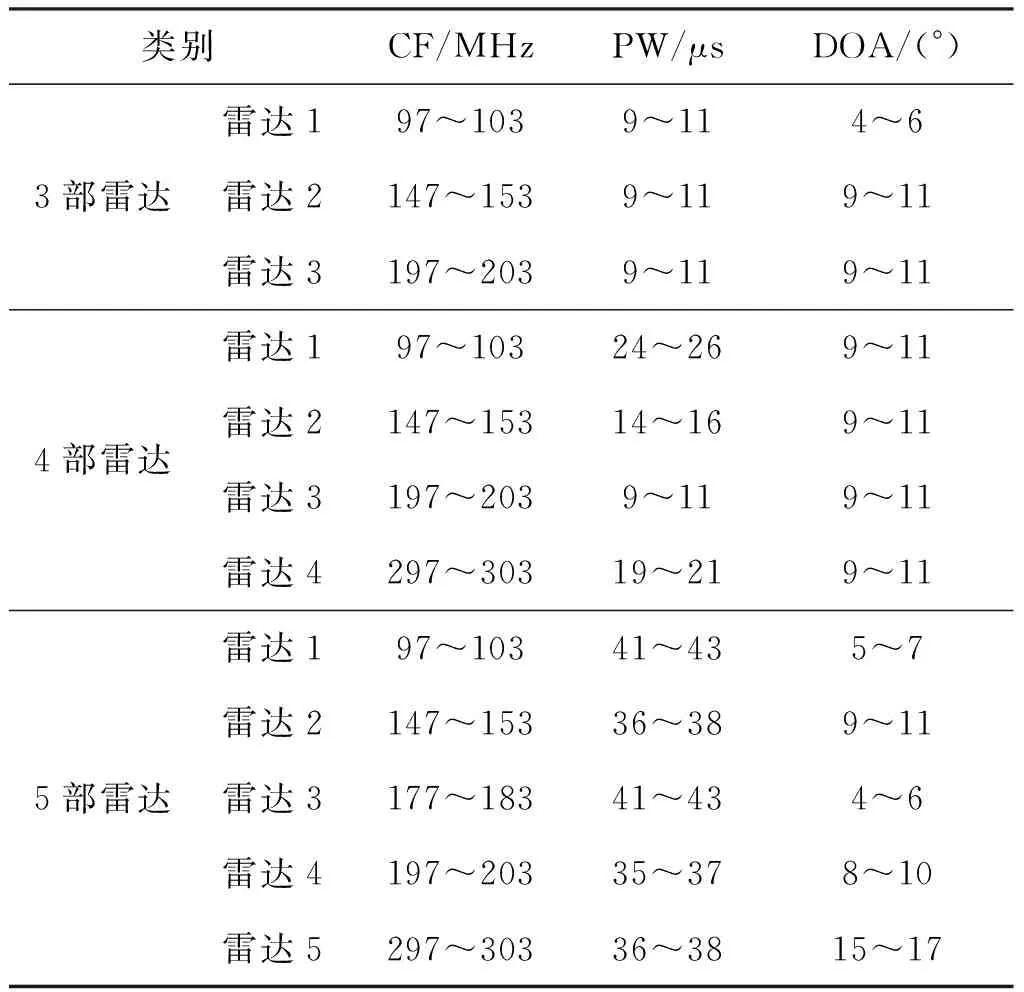
表1 参数设置Tab.1 Default values for parameters
4.1 DSets-DBSCAN算法与DSets-histeq比较
4.1.1 直方图均衡化
为了验证直方图均衡化消除了对σ的依赖,在下面的仿真中,将直方图均衡化前后的算法仿真结果进行比较。在直方图均衡化前首先对相似性矩阵进行离散化。
由于得到的相似性矩阵包含的元素数目多且元素精度大,若将其直接进行直方图均衡化,会导致算法计算量大大增加,算法仿真时间长;若离散化的精度太小,又会削弱直方图均衡化的意义。考虑到上述两个方面,在进行大量仿真实验后,本文将数据离散化为500个灰度等级。本文通过计算F-measure来评估聚类质量,并报告聚类结果。F-measure通过式(6)得到:
(6)

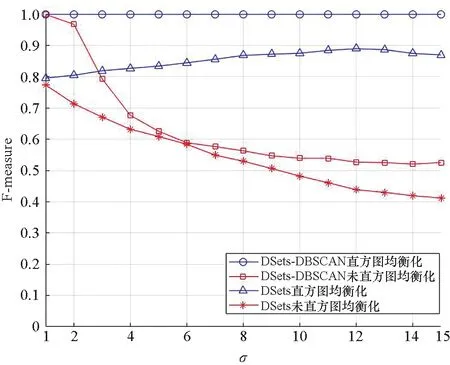
图2 直方图均衡化对算法的影响Fig.2 Influence of histogram equalization on algorithm

4.1.2 DSets-DBSCAN与DSets-histeq比较
为了查看DSets-DBSCAN算法是否解决了过度分割的问题,在图3中给出了DSets-histeq和DSets-DBSCAN这两个算法在相同输入下的聚类结果对比图。输入的虚假脉冲比例为0,并在仿真时设置MinPts=3。
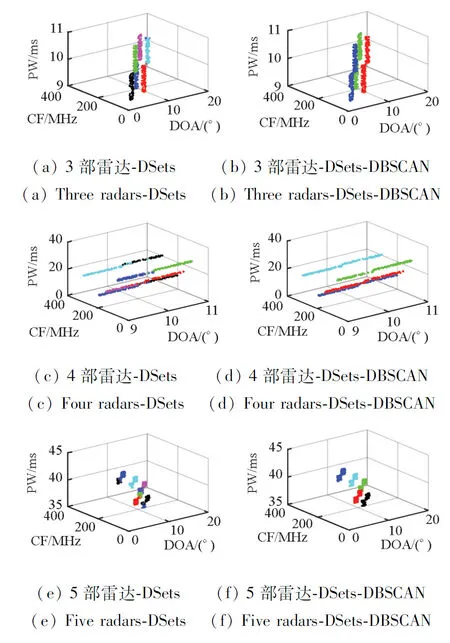
图3 雷达混合脉冲聚类结果Fig.3 Results of radar mixed pulse clustering
图3中每一个颜色都代表1部雷达。从图中可以看出,Dsets算法分选得到的雷达数目大于输入的雷达数目,本文算法分选得到的雷达数目与输入的雷达数目相等,由此可见,本文算法解决了过度分割的问题。为了更直观地给出两个算法的实际聚类数目,在表2中分别给出了两个算法获得的集群数量。从表中可以看出,DSets-DBSCAN中的集群数量比DSets-histeq中的集群数量少得多,与设置值相符,进一步验证了DSets-DBSCAN在克服过度分割方面的有效性。
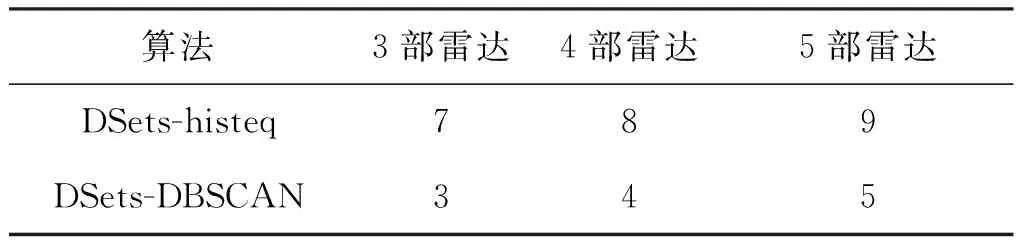
表2 两种算法分选结果数目对比Tab.2 Default values for parameters
4.2 DSets-DBSCAN与DBSCAN比较
在DSets-DBSCAN算法中,本文使用基于DBSCAN的集群扩展来克服过度分割并生成任意形状的集群。尽管DBSCAN算法的扩展需要MinPts和Eps作为输入,但在下面的仿真中可知,本文算法对MinPts参数设置不敏感,并根据优势集自适应地确定Eps。在下面的仿真中,通过对两个参数的分析,验证实践结果的有效性,如图4所示。
图4(a)给出了参数Eps对两个算法的影响,从图中可以看出,在一定的取值范围内,随着Eps值的增加,DBSCAN的聚类性能增强;由于DSets-DBSCAN算法中参数Eps是自适应确定的,所以参数Eps取值对DSets-DBSCAN聚类性能无影响。图4(b)中给出了参数MinPts对两个算法的影响,从图中可以看出,MinPts值在0~12之间变动时,DSets-DBSCAN算法性能不随着MinPts值改变。此外,从图4中可看出,DSets-DBSCAN算法的性能始终优于DBSCAN,这证明了本文算法中合并DSets算法和DBSCAN算法的有效性。

(a) Eps对算法的影响(a) Effect of Eps on the algorithm
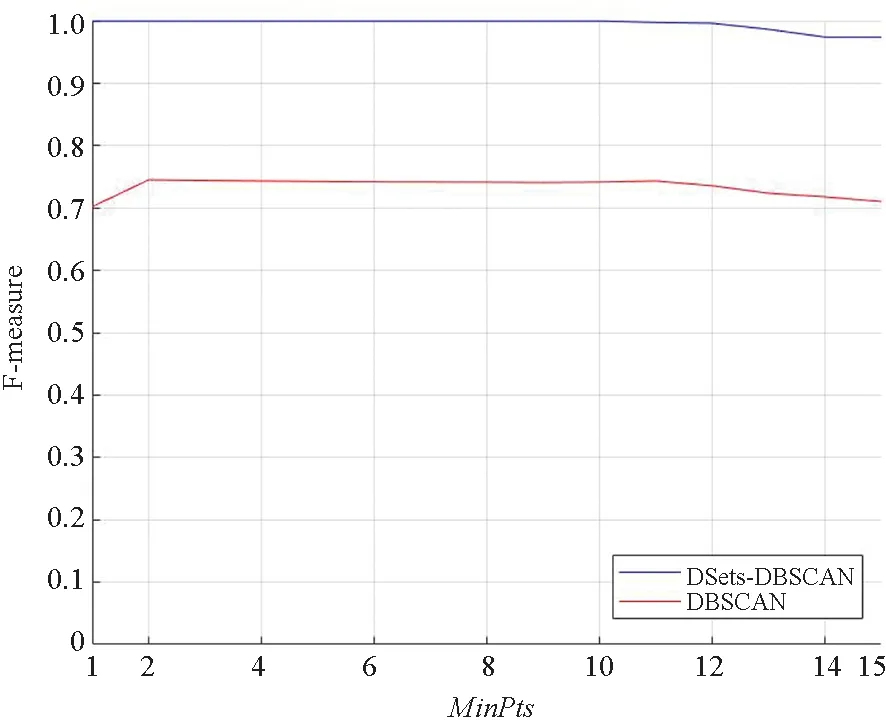
(b) MinPts对算法的影响(b) Effect of MinPts on the algorithm图4 DSets-DBSCAN和DBSCAN对比Fig.4 DSets-DBSCAN versus DBSCAN
4.3 本文算法与已有算法对比
为了评估所提方法在高虚假脉冲比例条件下的分选性能,图5给出了四种方法正确率平均F-measure值随虚假脉冲比例的变化曲线。从图5中可以看出,随虚假脉冲比例的增加,四种方法的分选性能都有不同程度的下降,但是所提方法在不同虚假脉冲比例的条件下性能都优于其他三种方法,且DSets-DBSCAN的聚类效果受虚假脉冲比例的影响较小。这是因为DSets-histeq聚类倾向于生成仅球形的超小簇,且输入至DBSCAN的参数Eps是由生成的超小簇自适应确定,所以算法只会将数据聚类,而不会将虚假脉冲聚类,这样得到的聚类结果受虚假脉冲比例的影响较小。

图5 不同虚假脉冲比例条件下分选正确率Fig.5 Sorting accuracy under different false pulse ratios
5 结论
对于没有先验信息的雷达信号,常规聚类方法的聚类性能严重依赖于外界输入的参数。本文提出了一种基于DSets-DBSCAN无参数聚类的雷达信号分选算法,该方法将直方图均衡化后的相似性矩阵应用于DSets,并自适应地确定DBSCAN的输入参数,实现了无参数聚类。通过实验仿真验证,在没有任何雷达信号的先验信息及输入参数的条件下,DSets-DBSCAN能够有效地聚类复杂脉冲信号环境中的雷达脉冲信号,实现了无参数聚类。同时,在虚假脉冲比例不超过80%的条件下,聚类正确率达到97.56%以上。通过实验仿真,验证了算法的可行性。

