密集环境中无人机协同机动飞行运动规划方法综述

牛轶峰，刘天晴，李 杰，贾圣德

(国防科技大学 智能科学学院, 湖南 长沙 410073)

近年来，小型多无人机(unmanned aerial vehicle, UAV)系统因其高协同性、多任务、低成本、高隐蔽等优势而备受关注。随着小型无人机的任务飞行高度降低，面对的地表环境的复杂程度和不确定性越来越高[1]，如树林、城市街道等。低空环境的密集性、不确定性对无人机的安全带来极大威胁，对无人机机动飞行避障能力提出较高的要求。而另一方面，机动避障使得飞行航迹存在重构问题，对协同任务的执行产生巨大干扰。因此，同时兼顾机动飞行与协同行为能力至关重要，其涉及机动飞行运动规划技术和协同航迹规划技术的交叉研究，本文将其称为协同机动飞行运动规划。

协同机动飞行运动规划是指为多架无人机规划出从初始位置到目标位置的状态/动作序列，该序列满足无人机机动能力、躲避环境障碍，以及保持过程中或末端的状态协同。在机动飞行运动规划技术和协同航迹规划技术两个领域已有一些综述[2-6]，但对于二者交叉形成的协同机动飞行运动规划的研究综述较少。本文基于当前飞行试验支撑的规划方法框架，对其中涉及的子模块的基本原理、重要方法和前沿研究展开综述，试图将机动和协同两个领域的研究有机结合，为交叉领域研究的后续工作提供一些有益的启示。

1 概述

密集环境是指环境中存在大量无规则的不确定的密集障碍物，如树木、楼宇等，无人机需要实时感知环境并做出高质量的运动规划。目前的主流框架为建图+前端(路径规划或混合规划)+后端(轨迹规划)+路径或轨迹协同因素考虑，如图1所示。传统上认为路径规划和轨迹规划的区别在于：前者的规划结果只包含空间信息，不包含时间信息；而后者包含空间和时间信息。但随着近年来基于运动力学的规划器(kinodynamic planner)的发展，考虑时间因素的动力学约束被纳入路径规划过程，原有的路径和轨迹概念逐渐模糊。

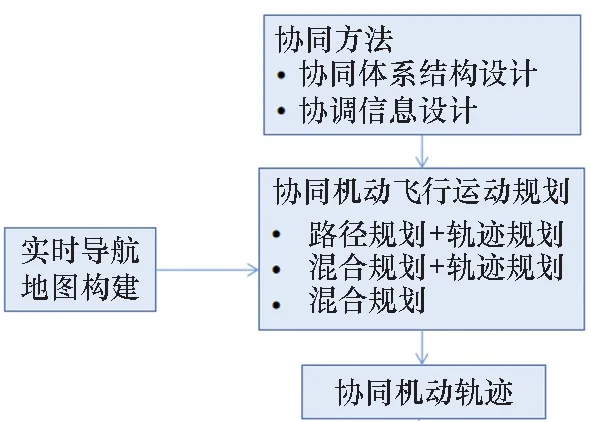
图1 无人机协同机动飞行主流框架元素Fig.1 Popular frame of cooperative maneuvering flight for UAVs

本文把相关概念划分为：路径规划、轨迹规划、混合规划(方法对比见表1)，其划分标准为：由于无人机运动过程中的状态变化是连续的，在无限的状态空间中寻找一个状态转移序列是无法实现的，所以需要通过一些方法来把无限的空间转化为有限的空间，这种转化方式和转换后有限空间的不同可作为划分路径规划、轨迹规划、混合规划的标准。路径规划对连续的规划空间进行离散，其结果路径是离散空间中的节点的序列；轨迹规划对连续空间进行参数化表达，进而将无限的规划空间转化为有限的参数空间，其结果轨迹是参数化表达的曲线；混合规划首先建立参数化表达的运动基元或轨迹片段，基于离散规划问题的求解方法得到动作基元或轨迹片段序列。其中常见的规划空间有3维位置空间、位姿空间(如SE(3))、动作空间等。

表1 运动规划方法对比Tab.1 Comparison of motion planning methods

需要注意的是，在上述框架之外存在一些相关联的研究但不在本综述范围内，包括：被建模为规则几何体障碍环境中的避障规划[7-8]，因为这些方法缺少对不确定环境的感知和应对能力；协同控制+基于反应式的避障方法[9]，难以较好应对密集障碍；基于学习的端到端的密集环境中的避障[10-12]，难以多机协同；基于学习的多智能体协同控制方法[13-15]，尚无法应对复杂密集的环境；基于模型预测控制的方法[16-18]，控制层而非规划层方法，不对其进行介绍。

本节将从实时建图、路径规划、轨迹规划、混合规划、多航迹或轨迹的协同规划五个方面展开综述。

2 实时导航地图构建

实时地图主要有稀疏路标地图、稠密地图、语义地图等，稠密地图由于可以比较完整地描述障碍信息，所以常被用于导航和避障。稠密地图的构建通常是指利用传感器获取的环境深度信息建立便于运动规划的地图。目前，稠密地图主要包括：点云地图(point cloud map)、占用栅格地图(occupancy grid map)、符号距离场(signed distance field, SDF)、飞行走廊(flight corridor)，如图2所示。

(a)点云地图[19] (b)二维栅格地图(a)Point dloud map[19] (b)Occupancy grid map

(a)二维符号地图 (b)多边形飞行走廊(c)Signed distance field (d)Polyhedron flight corridor图2 稠密地图Fig.2 Dense map

点云地图为深度传感器直接获得的深度点经过滤波、坐标转换等处理后构成的由空间点组成的地图。点云地图所提供的环境信息对于规划算法来说较难利用，优势在于容易获得、构建时算力消耗少。文献[19]设计了基于KD-Tree点云地图的点对点的碰撞检查方法来实现避障。文献[20]对历史深度图像和姿态信息进行记录，通过对历史信息的回溯去估计更精确的障碍信息以应对无人机自身的姿态不确定性状况。这两种方法都只适用于障碍是孤立，并且数量较少的环境。

对点云进行空间离散，存在障碍点的离散单元被标记为占用，则形成占用栅格地图。占用栅格地图访问简单快速，被广泛应用于路径规划、混合规划，但其占用的存储资源较大，并且随着地图精度的提高而爆炸式增长。针对占用栅格地图的以上缺点，八叉树地图(octo-map)[21]被提出，它将栅格地图按照八叉树进行压缩，即将空间栅格按照类似于树的数据结构方从大栅格到细分小栅格方式进行存储，大栅格中若不存在小障碍，则不会对该栅格进行细分。由于环境中障碍和自由空间通常是连续的，所以八叉树地图可以极大程度地降低存储资源的消耗，但访问难度比普通占用栅格地图高。文献[22]提出了一种使用循环缓冲区来进行局部八叉树地图构建的方法，从而实现局部地图能够实时更新，并以无人机为中心移动。类似的还有利用哈希表(hash table)降低存储的体素哈希地图[23]、利用跳表(skip list)建立的SkiMap[24]等。

符号距离场在栅格地图的基础上记录了空间内每个点到最近障碍的距离，起源于计算机图形学[25]，常应用于基于优化的轨迹规划算法。符号距离场与人工势场法(artificial potential field, APF)[26]中的势场同样提供环境梯度信息，区别在于前者是离散估计，而后者是数学解析式。文献[25]使用截断符号距离场(truncated signed distance field, TSDF)重建高分辨率的3D场景，它在占用栅格地图的基础上，计算从相机视线(射线)上每个栅格到其所在视线上的最近障碍的距离，在障碍以外距离标为正值，在障碍以内距离标为负值，零等值面表示障碍表面。欧氏符号距离场(euclidean signed distance field, ESDF)是目前广泛应用于自主导航研究领域的一类地图，它与TSDF的区别在于，地图的每个栅格的数值为其到最近的障碍的距离，而不是沿着射线上的距离[27]，所以ESDF的梯度比TSDF的更加连续，更适合提供基于优化的规划方法中的环境梯度信息。SDF能够为轨迹规划提供丰富的环境信息，但构建时计算量大，环境梯度通常具有明显的非凸性，对规划的实时性和优化求解产生挑战。

飞行走廊是根据点云、栅格地图等标记障碍的地图建立一系列无障碍区域，这些区域通常具有凸形状并且相互连接，从而形成一个能够自由飞行穿梭的“走廊”。典型的飞行走廊的凸形状有立方体、不规则凸多面体、球等，如图2(c)、图2(d)所示。文献[28]基于八叉树地图建立由轴平行的立方体构成的飞行走廊。立方体内部区域可以直接由立方体面的不等式表达，故飞行走廊束可以直接作为轨迹优化的不等式约束。文献[29]提出了根据实时定位与建图(simultaneous localization and mapping, SLAM)过程中所使用的特征点扩展得到一系列面相切的凸多面体，然后在这系列凸多面体内生成以直线连接的无障碍拓扑结构用于规划路径。文献[30]在文献[28]的基础上进行扩展，提出了使用不规则凸多面体构建飞行走廊并通过迭代的凸性质检查和空间点扩展进行构建的方法，以解决复杂环境中使用立方体建立飞行走廊导致的大量安全区域不能被纳入飞行走廊的不足。文献[31-32]提出在点云数据的基础上实时构建由球连接形成的飞行走廊。

随着机载算力的提升和传感器的集成，构建稠密地图的耗时大大缩短，推动基于实时稠密地图的复杂动作运动规划成为无人机机动避障领域广泛应用的解决方案。该类地图构建方法与运动规划算法的选择密切相关，如何能够更快速地构建更有便于规划算法求解的实时地图，是研究的重点和发展方向。

3 机动飞行运动规划

3.1 路径规划

路径规划是指在离散的状态空间中搜索到一条从初始状态到目标状态之间的状态转移序列，可分为两类：基于采样的方法、基于搜索的方法，其差别在于将连续空间离散化的方法不同。

基于采样的路径规划方法通过在状态空间中进行随机采样得到有限的采样点，从而获得有限的状态空间；将采样点以特定的规则连接构成图或者树，进而搜索得到路径。研究的关注点在于如何采样、以怎样的规则构成图或者树。最具代表性的两类方法是概率地图法(probabilistic road-map, PRM)[33]和快速扩展随机树(rapidly-exploring random tree，RRT)[34]。PRM通过在可行的状态空间中生产成随机采样，在临近采样点之间建立连接构建拓扑图，在图中搜索得到连接起始状态和目标状态路径。文献[35-36]提出推迟节点间连接的碰撞检查，只检查路径周围的连接碰撞性。RRT通过采样构建状态树，并在搜索状态树的同时进行新的状态点采样，通过将新得到的状态点连接到状态树上最近状态点来扩展状态树，但RRT不具备渐进最优性[37]。RRT有很多衍生算法，并得到广泛的应用，包括PRG[37]、RRT*[38]、Informed-RRT*[39]等算法。PRG[37]算法对RRT树的扩展方式进行了改进，通过对树的搜索确定新生成的状态点连到状态树上的哪个点，而不是最近的点。RRT-Connect[40]从初始点和目标点扩展两棵树。RRT*[38]引入了重新连接机制，以确保状态树上的根节点到每个叶节点的路径都是最短的，如图3(a)所示。Informed-RRT*[39]把采样点范围限制在以初始状态点和目标状态点为焦点的椭圆里，从而极大提升收敛速率，如图3(b)所示。除此之外还有一些其他的方法，如RRT*-Smart[41]、Parallel-RRT[42]、RRT*-Connect[43]、LBT-RRT[44]等。

基于搜索的路径规划算法以特定的规则预先对状态空间进行直接离散，从而获得有限空间。在离散状态空间中以一定的规则拓展得到树，然后基于一定的规则对树进行搜索，直到找到连接初值状态节点和目标状态节点的状态序列。对于无权重的树，搜索方法可采用广度优先搜索(breadth-first search, BFS)和深度优先搜索(depth-first search, DFS )。BFS采用先进先出的队列规则，能够保证路径的最优性；DFS采用先进后出的栈规则，不能保证得到的路径是最优的。对于有权重的树，采用Dijkstra算法[45]搜索，优先扩展树上到初始节点代价最小的节点。A*[46]算法在Dijkstra的基础上增加了对扩展点到目标点代价的启发式估计，即优先扩展到初始点代价和到目标值启发式估计之和最小的节点，是目前基于搜索的算法中使用较为广泛的算法。A*算法得到最优解的条件是对于所有节点，满足启发式函数小于真实代价函数；A*算法的速率和空间复杂度主要受启发式估计的影响，好的启发式估计可以减少算法扩展的节点数、提升计算速率。A*算法有许多扩展算法。Lifelong Planning A*(LPA*)[47]算法添加了对树上的节点生存时间的考虑来限制树的大小。D*Lite[48]算法添加了对树的局部修改来克服重规划过程中需要重新生成整个树的重复计算。跳点搜索(jump point search， JPS)算法[49]改变了传统的BFS、DFS、A*等算法的扩展方式，它的扩展方式为优先斜线其次垂直和横向并且可以跨越多个点，适用于网格式的地图，如图3(c)所示。文献[50-51]使用JPS作为全局规划器或重规划器，以实现无人机避障飞行。

(a) RRT*[39] (b) Informed-RRT*[39]

(c) JPS[49]图3 几种路径规划方法Fig.3 Several path planning methods

近些年，离散状态空间中的路径规划研究较为成熟并逐渐减少。随着计算机算力的提升和问题难度的增大，研究重点从过去的如何提高求解效率问题转变为如何让求解结果满足更多的可行性条件。方法层面，在原有的路径规划方法基础上，扩大了状态空间维数、引入了优化方法，发展出了一系列混合规划方法(如Kinodynamic RRT*、hybrid A*，详见1.4节)。传统的路径规划求解方法和思想被巧妙地运用到混合规划方法中。

3.2 轨迹规划

轨迹规划在环境障碍、无人机运动力学、特定飞行任务要求等约束条件下，求解一条满足燃料消耗最小、稳定性最高等优化目标的带时间信息的曲线，即最优轨迹。对于较长距离的规划，通常由路径规划提供初始点估计以提高求解成功率和速率。通过使用参数表达的曲线，无限的连续空间被转化为有限的曲线参数空间，新的参数空间因曲线的表达方式不同而不同。最优轨迹是指在特定的曲线表达方式下对优化目标的最优解，而非所有可能的轨迹中的最优解，即同一个规划问题采用不同的曲线进行表达，求解得到的曲线并不重合。常见的轨迹表达方式有分段多项式曲线、贝塞尔曲线、B样条等。环境障碍信息通常以不等式约束(硬约束方法)或者代价函数(软约束方法)的方式被建模到优化问题中。硬约束方法将环境信息作为优化问题的约束条件，所以优化问题一旦有解就可以得到安全的避障轨迹，然而带约束的优化问题的求解难度较大。软约束方法通常利用梯度地图将环境信息建模到优化问题的目标函数中，从而建立无约束优化问题。因为障碍约束被作为被优化的指标而不是强制性的约束，所以理论上不能保证轨迹一定不会撞到障碍。此外，梯度地图通常具有非凸性，给问题求解带来挑战。还有一些不显示将环境信息建模到优化问题的方法。

Mellinger等提出minimum snap方法[52]是无人机轨迹规划应用领域的里程碑之作，实现了旋翼无人机在室内环境中机动飞行。该方法利用旋翼无人机的微分平坦性，以无人机的位置和偏航角以及其导数作为状态变量来描述系统的运动学方程；使用分段多项式来描述轨迹，并建立最小化四阶位置导数的优化目标函数，从而建立轨迹优化问题模型，其实验如图4(a)所示。文献[53]在minimum snap基础上实现了前端+后端的运动规划实验。该文章推导出minimum snap最优轨迹的二次型最优解，从而将优化问题转换为构造求解问题。这种方法在构造过程中使用了具有物理含义的中间状态量来代替文献[52]中的无意义的多项式系数，从而提高了数值稳定性。此外，该文章阐述了minimum snap方法使用中面临着两个重要挑战：①分段多项式轨迹的时间分配是事先确定的，而受限于多项式曲线本身的性质，时间分配的结果直接影响轨迹形状，文章提出了一种通过求解最优问题的时间自动分配方案；②尽管由前段路径规划生成的路径点在安全空间，但后端生成的轨迹仍然可能撞到障碍，文章给出了添加关键路径点后重新生成轨迹的解决方案。文献[54]提出了通过建立安全的飞行走廊来解决挑战②，并引入平方和(sum-of-squares, SOS)算法保证分段多项式轨迹保持在飞行走廊内。文献[28]基于飞行走廊的思想，提出了基于八叉树的飞行走廊生成方式，并设计了轨迹规划的迭代算法，来应对约束过多而带来的优化问题过于复杂的挑战。文献[55]在文献[28]基础上提出时间和空间交替优化的方式以应对挑战①，该方法还应用在工作[30,56]中，实现了室内外密集环境中的旋翼飞机机动穿行。

文献[57]使用文献[53]提出的分段多项式轨迹表达方式，用描述轨迹平滑程度的导数和描述环境信息的ESDF设计代价函数，建立无约束的优化问题模型，求解避障的轨迹。文献[22]提出的ewok规划器使用均匀B样条表达轨迹，采用循环缓冲的ESDF描述环境，将动力学的硬约束转化为指数函数的软约束加入优化目标函数，从而建立无约束的优化问题模型，实现了旋翼无人机树林中的穿行。文献[58]在ESDF上用均匀B样条表达轨迹进行空间优化，然后使用非均匀B样条表达轨迹进行迭代优化以调整时间分配，以应对挑战①。

以上方法需要建立飞行走廊或ESDF，需要消耗大量算力，所以一些不使用复杂地图的方法被提出。文献[59]提出的EGO-planner针对与障碍发生冲突的B样条轨迹区域，对B样条控制点施加由障碍内向障碍外的“排斥力”以对轨迹进行变形，直到轨迹与障碍不冲突，其中 “排斥力”通过A*算法规划出的安全路径生成。

除了以上提到的传统轨迹表达方式，文献[60]提出一种新的轨迹表达方式：最小控制(minimum control, MINCO)轨迹类，可以实现直接解析计算特定阶导数平方和最小的轨迹，从而实现的计算速度提升一个数量，被应用于一系列工作中[61-64]，实现了单架飞机穿越狭窄窗格的高机动飞行和多架旋翼飞机在密集环境中的协同机动飞行，其实验效果如图4(b)所示。

以上算法在旋翼平台上得到了实飞验证，而在固定翼平台受限于飞行特性和目前高空飞行的应用背景，相关机动飞行的试验相对较少。Bry等[65]进行了固定翼的飞行试验，在文献[52]规划算法的基础上针对固定翼飞机飞行特性进行了改造，实现了小型固定翼无人机以恒定速度在地下车库中绕柱飞行。该方法设定固定翼飞机在平面以恒定速度飞行，首先基于文献[52]的轨迹规划方法生成分段多项式轨迹，然后使用Dubins曲线逼近多项式轨迹，控制固定翼飞机跟踪Dubins曲线实现避障。Dubins曲线是由圆弧和直线连接而成的曲线，意味着无人机只有以恒定角速率转弯或直行两种运动状态，跟踪控制难度低，其实验场景如图4(c)所示。

(a) 多项式轨迹规划飞行试验[52](a) Flight test for polynomial trajectory planning[52]

(b) MINCO飞行试验[60](b) Flight test for MINCO[60]

(c) Dubins曲线飞行试验[65](c) Flight test for Dubins curve[65]图4 轨迹规划飞行试验Fig.4 Flight test for trajectory planning

本节所阐述的轨迹规划方法重在使用复杂的高阶曲线生成满足机动约束的可直接执行的轨迹。随着无人机的底层控制性能的不断提升和机动局限的不断缩小，无人机高质量完成轨迹的能力不断提升，推动了轨迹规划结果的复杂度和精细度的提升。未来，针对无人机规划问题本身特点的更高效的轨迹表达方式和关联求解方法将逐步取代通用曲线和通用求解方法，从而进一步提升轨迹质量和求解效率。

3.3 混合规划

混合规划方法的主要思想是将满足动力学特性的轨迹或动作片段进行拼接，从而生成较长距离的连续轨迹或动作序列，规划结果基本满足动力学约束和环境障碍约束，通常可以被无人机直接执行。轨迹或动作片段的常见的生成方式主要有：①对控制量进行离散，建立无人机在特定控制量或控制量序列在特定时间段下控制形成的轨迹集合；②求解最优化问题(如两点边界值最优问题、未来一段时间内的可达范围)，从而形成两个状态点之间的连接轨迹；③由实验数据获取运动基元。混合规划有多个英文名称，主要包括状态晶格(state lattice)法、基于运动力学的运动规划(kinodynamic motion planning)、混合的规划(hybrid planning)、基于轨迹库(trajectory library)的规划、基于运动基元(motion primitives)的规划，它们的核心思想相同，发展来源和方案有所不同。文献[66]提出状态晶格法和基于控制空间运动基元方法。状态晶格法首先生成离散的状态空间，然后在离散的空间状态点之间生成轨迹片段，并且相邻轨迹片段保持连通性，如采用圆弧与直线作为轨迹片段连接2维平面内晶格定点，然后搜索得到可行轨迹。基于控制空间运动基元的方法将控制输入离散为4个方向的控制量，进而形成动作空间，如图5(a)所示；在动作空间内搜索，得到从初始状态到预期状态的控制输入序列。文献[67]在SE(3)空间内采用基于搜索的离散控制方法实现了旋翼无人机利用瞬时倾角穿过小于无人机直径的门缝。文献[68-69]提出的Kinodynamic RRT*在RRT*中引入对路径运动学可行性的考虑，将状态树上的点与点的连接改为满足无人机的动力学的轨迹段，该轨迹段由两点边界值优化问题求得，最终实现了线性化无人机模型的10维状态(位置3维、速度3维、滚转角和俯仰角及其导数4维)运动规划。文献[70]在Kinodynamic RRT*的基础上引入了重连接和重采样机制，并在ESDF上实现轨迹生成。文献[71]进一步引入对轨迹的时间和空间的优化，通过求解关于时间和空间的轨迹最优化问题模型对RRT节点位置进行优化，从而获得时间和空间都更优质的轨迹。文献[72]提出的Hybrid A*方法首先并被应用到无人车路径规划上，它在A*的基础上加入了机器人的运动学信息的考量，其构建的树中的节点不是简单的3维空间状态信息，还包括了无人车的朝向信息；启发式函数考虑了无人车的运动代价，树节点改为空间离散方格中的某一点而不是中心点，如图5(b)所示。该方法也被应用于无人机领域，Han等[56]和Zhou等[58]采用Hybird A*方法作为规划前端实现了旋翼无人机在密集环境下的避障机动飞行。文献[73]提出了基于轨迹库的规划控制方法，轨迹库内包括两种类型的轨迹：轨迹基元(trim trajectory)、机动自动机(maneuver automation)，分别用于平衡态的轨迹描述和连接运动基元的机动动作，该规划框架可以适用于时变的非线性的欠驱动系统(如典型的固定翼无人机系统)。文献[74]基于该方法实现了三角翼无人机对独立树木的躲避，以及不到50%成功率的稀树林近距离的机动避障。文献[75]设计了有限的开环轨迹库，显示最小化最坏情况下的可达集，并提供了一种顺序组成轨迹的方法以保证实时安全性，在室内条件下实现无人车和小型固定翼无人机在密集环境中的避障飞行。文献[76]设计了两种运动基元，一种用于平稳的转向，另一种用于密集障碍的即时转向，采用基于模型预测控制的动态规划框架，实现了微型固定翼飞机在室内的避障飞行，如图5(c)所示。

(a)基于控制空间生成的运动基元轨迹[63](a)Trajectory consisting of motion primitives based on control set[63]

(b) Hybrid A*方法规划过程[72](b) Process of Hybrid A*[72]

(c)一咱固定翼飞机的运动基元[76](c)A kind of motion primitive for fixed-wing[76]图5 几种混合规划方法Fig.5 Several hybrid planning methods

随着搜索技术和优化技术的发展，以及算力的提升，混合规划的复杂度、实时性和规划距离得到了显著的提升，从而实现在更密集的环境障碍下的机动飞行。此外，相比于轨迹规划，混合规划牺牲规划结果的全局最优性，获得了机动性、实时性和稳定性的提升，更适用于飞行速度较高、控制难度较大、机动局限性较大的固定翼无人机。

4 多航迹或轨迹的协同规划

多机协同航迹或轨迹规划方法是研究在环境、任务、机动等约束下，寻找多无人机系统的最佳航迹策略，其研究的问题涉及如何设计协同体系结构、如何设计协调信息和利用方式等，其关键在于处理好多条航迹或轨迹在时间、空间和任务层面的协调关系。协同飞行问题研究主要集中在航空领域，该领域中通常使用“航线”“航迹”等表达飞行规划结果，与前文所述的“路径”“轨迹”概念大体一致，具体如下。

航迹规划方法从航迹表达维数角度可分为2维、3维、4维航迹规划3种。2维航迹规划在2维平面内进行，由于规划维数低，通常被用于无人机飞行高度固定条件下的长距离运动规划。3维航迹规划在3维空间内进行，其航迹间协调方式包括两种：速度控制和几何空间控制。4维航迹规划在3维空间+时间的4个维度上进行，与3维航迹规划通常忽略时间约束或者对到达时间进行区间约束不同，4维航迹规划可以实现更严格的到达时间控制，同时可以对整个航迹区间进行速度规划，因此航迹间协调可以直接通过航迹规划实现。但由于多了1个时间维度，4维航迹规划建模与求解的困难程度普遍大于3维航迹规划。前文所提轨迹的含义同4维航迹。文献[77]采用2维航迹+混合速度控制协同跟踪的方法实现飞行角速度和速度受限的固定翼集群协同飞行。文献[78-80]采用3维航迹+速度控制的方法规划协同航迹，采用毕达哥拉斯速端曲线描述3维航迹，另外使用贝塞尔曲线来描述航迹的时间元素，并进一步转化为速度控制，仅通过优化调整描述时间元素的贝塞尔曲线来实现飞机间的协调。该方法能够将空间与时间分开规划是因为底层控制器将姿态和速度完全解耦：速度调整只被用来进行协同，姿态调整只被用来进行空间控制。该方法适用于速度和姿态耦合度低的规划控制问题，但难以应对高机动轨迹等速度姿态耦合程度高的问题。文献[81]采用3维航迹+几何空间协同的方式实现飞行器的协同航迹规划，该方法假定飞行器的飞行速度恒定，采用分段贝塞尔曲线描述航迹，将每个飞行器的航迹的总长度作为协调变量，优化生成满足任务要求的最佳一致长度，该方法适用于速度变化较小的飞行器。文献[82]研究了基于生物启发的多无人机协同4维航迹规划方法，提出了基于tau制导策略的4维航迹规划方法，仿真中实现较高精度的4维飞行。

依据体系结构，多无人机协同航迹规划算法可分为集中式架构和分布式架构。集中式规划方法需要多无人机系统中存在中心计算单元，中心单元可获得整个系统的状态信息，并将规划结果传递给每架无人机。集中式规划方法由于拥有系统的全部信息且中心节点一般具有较强的算力支撑，可使用一些求解性能较强的算法求解协同规划问题规划出全局最优航迹，如基于遗传算法的协同航迹规划[83]、基于混合人工势场-蚁群优化方法的协同航迹规划[84]、基于混合整数规划的协同避障[85]、基于图方法的协同航迹规划[86]等。集中式架构计算量大、计算时间长，严重依赖通信系统，且中心节点一旦崩溃则整个系统将会崩溃。针对这些劣势，分布式架构具有突出优势而备受关注。分布式架构中没有中心计算单元，每架无人机计算生成自己的航迹或轨迹，具有自适应、自组织和良好的协调性能[87]，相比于集中式架构，更适合于在线的实时规划。分布式架构可以是通过对集中方法进行并行设计得到，或直接设计分布式算法。与集中式方法不同，分布式方法在实现协同过程中需要重点关注信息交互方式和内容的设计。文献[61]按照优先级的时序顺序依次进行规划，规划结束之后把自己的状态和规划结果广播给集群里的每架无人机，每个无人机基于梯度的优化方法优化生成自己的轨迹，实现复杂环境中多机协同飞行，该算法在飞行试验和仿真实验中都实现了以相同进度完成飞行任务并保证了飞行的安全。该方法通信量较大，通信条件较为理想，只适用于近距离飞行。文献[7]采用两步迭代，第一步在没有其他无人机信息的情况下基于滚动优化最优控制生成自身轨迹并将其发给其他无人机，第二步基于上一步生成的所有无人机的轨迹对自己的轨迹进行协调调整，如图6所示。文献[88]提出了协同变量和协同函数的方法，能够高效地利用通信和计算资源，得到较为广泛的应用。文献[89]设定了一个沿航迹运动的“虚拟目标”以作为协调变量，虚拟目标的位置由速度协调方程确定，并作为无人机轨迹跟踪控制的目标。

图6 分布式两阶段协同框架Fig.6 Flowchart of the 2-stages decentralized coordination strategy

本节重点关注能够与避障飞行相结合的协同和通信框架，而非近些年研究较多的自由空域中的编队保持或集群避碰的协同问题。随着单机自主飞行能力的提升和飞行任务的复杂性和对抗性的提升，分布式协同方法将成为协同机动飞行的主流协同框架。而随着任务环境愈发密集复杂，无人机机动动作愈发逼近极限，为完成协同任务而能够做出的飞行调整空间愈小，如何在这种情况下完成协同任务，将成为协同框架和方法研究的关注点。

5 结论及未来研究工作展望

本文基于当前已有飞行试验数据支撑的无人机协同机动飞行运动规划框架，对其中涉及的子模块的基本原理、重要方法和前沿研究展开综述。对于密集环境中的协同机动飞行运动规划技术，已有研究表明其发展路线有两个方向：在拥有机动避障能力的基础上增加协同性，在拥有协同能力的基础上增加机动避障能力。从现有的研究成果中可以发现，支撑该技术研究的航迹协同规划研究和机动飞行运动规划研究已有较长的历史和丰富的成果，但这两个研究领域的交叉融合还有很大的研究空间。

5.1 实时导航地图高效构建方法

导航地图的构建耗时和表达方式对运动规划的效率质量有很大影响。为了提高实时导航地图构建效率，可以根据规划问题本身特点(如轨迹表示方法、优化方法的选择)在复杂的环境中有选择性地选取规划使用的关键信息进行地图构建。设计高效的地图表达方式，运用数据结构相关方法，在算法的时间与空间复杂性上做平衡。引入最优化方法、人工智能等方法，提升构建速率。

5.2 满足协同和避障约束的飞行轨迹实时优化方法

将协同信息和避障约束同时并融洽地建立在一个轨迹优化问题中，根据协同机动的特性选择高效的轨迹表达方式，例如能够同时实现时间和空间表征的4维航迹；根据所选择的航迹表达方式，结合一致性理论、最优化理论等建立优化问题约束和优化目标；根据问题特性设计合适的优化器进行快速求解，以满足实时性要求。

5.3 适应机动飞行特性的最小协同方法

过去和当前无人机协同问题研究更多关注无障碍空域的编队保持和机间碰撞。然而无人机在密集环境中机动飞行时常需要规避不确定障碍而进行空间上的重规划，对时间上协同产生巨大挑战，需要设计高效协同架构以应对机动飞行具有高不确定性和高实时性的特点，根据一致性理论、信息论等设计最少的协调信息以应对在复杂地面环境中通信量受限情况，从而完成兼顾自主机动避障的飞行末端或过程协同任务。