无人机集群作战中连续时间Markov链模型的求解方法
黄树彩,谢家豪,韦道知,张曌宇
(空军工程大学 防空反导学院, 陕西 西安 710051)
近年来爆发的纳卡冲突表明无人机集群作战将在未来军事领域中对作战模式产生颠覆性变革,同时也因其在未来战场具有协同探测、协同攻击、干扰压制等方面的巨大优势,使其成为一支不可忽视的新质力量。
而当前国内外针对无人机集群作战过程的研究主要从框架建模、技术建模和数学解析建模三个层面展开。Giles[1]提出一种自上而下兼有条令与设计一体化的集成框架,该框架下无人机集群作战去中心化和扁平化,同时也研究了指控架构。文献[2-5]主要针对无人机任务规划中的任务分配问题展开研究,主要包括群智能算法、基于图论的任务分配方法、合同算法和拍卖算法等。文献[6-9]主要针对无人机任务规划中的航迹规划问题展开研究,主要包括基于数学模型的规划方法,如启发式算法、搜索法等,还包括基于学习的规划方法[10-12],如基于先验知识学习方法和基于强化学习方法等。文献[13-15]主要针对载人作战飞机(manned combat aircraft vehicle, MCAVs)与无人作战飞机(unmanned combat aircraft vehicle, UCAVs)共同形成协同作战体系,将该系统划分为任务级、集群级和系统级三个层次,并建立相应的数学模型。为了求解这些模型,提出量子人工蜂群算法(quantum artificial bee colony algorithm, QABC)、两阶段贪婪策略(two stage greedy strategy, TSGS)等算法来验证所提算法的有效性和优越性。文献[16-18]利用概率论,重点通过建模对无人机集群的作战效能进行分析, López等[19]学者也对无人作战飞机在格斗作战中的效用进行研究,使用基于代表性制导律和博弈论算法的自主决策方法来评估无人作战飞机在测向作战中的有效性。但是这些研究并未对无人机集群作战全过程进行建模分析,同时也未考虑在Markov模型求解过程中速率矩阵的稀疏性问题。
为解决矩阵的稀疏性问题,国内外的研究大多采用压缩存储的方法。常用的压缩存储方法[20-22]主要有行压缩存储、列压缩存储和行飞快存储等,但是这些方法并未能够针对Markov模型特点进行研究。Markov模型的常用求解方法[21,23-24]有很多,如常微分方程法、多项式法、矩阵分解法、Krylov子空间方法,但是这些方法大都不适用于稀疏矩阵的求解。Reibman等[25]在研究排队系统时通过实验验证Runge-Kutta、Liou方法和随机化三种方法可以求解状态数大于600时的Markov模型。Rauzy[26]指出取合适参数的前向Euler方法适用于Markov模型的求解。上述方法虽然可以有效求解Markov模型,但是对于大型稀疏矩阵,仍存在存储量和计算量巨大的问题,即需要寻求一种可以提高计算效率的算法。
针对求解Markov模型中存储量大、计算速率低的问题,本文提出一种基于行压缩存储的四阶Runge-Kutta算法。分阶段建立无人机集群作战过程的连续时间马尔可夫链(continuous time Markov chain, CTMC)模型,运用四阶Runge-Kutta法对Markov模型求解,对于求解过程中速率转移矩阵的稀疏特性运用基于行压缩存储的算法优化求解速率,进一步压缩存储空间、提高计算效率。
1 无人机集群作战流程设计
目前,国内外对于无人机集群的概念尚未形成统一描述,本文从无人机集群目标特性及其作战特点出发,在参考国内外大量文献的基础上将无人机集群的概念定义为:具有互联互通功能的多架无人机为执行某一作战任务,按照一定的指挥控制规则,彼此间协同配合达到作战目的的集合体。
无人机集群主要由运载平台、无人机及其载荷、运载指控终端和数据链终端四个部分组成,如图1所示。
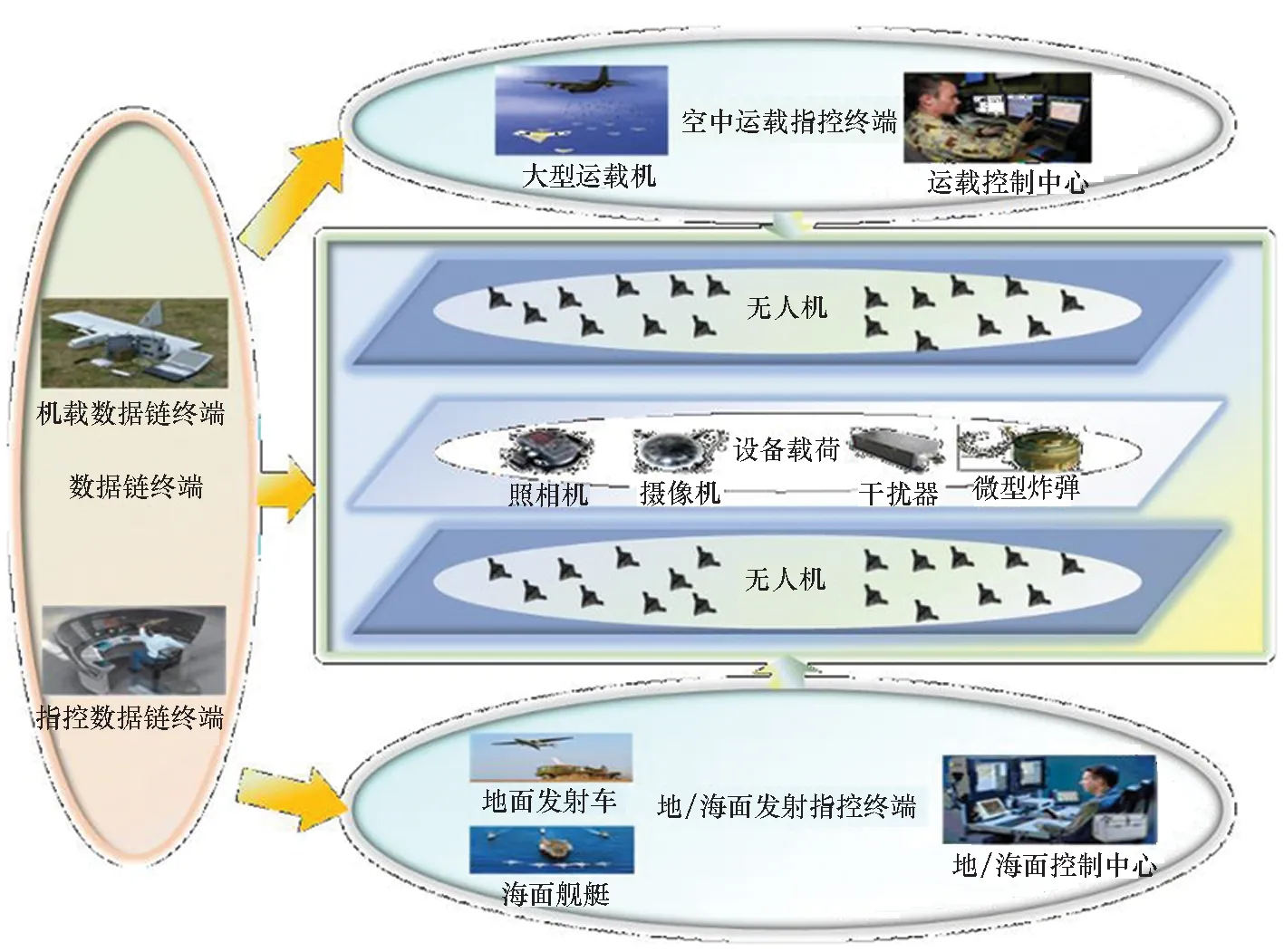
图1 无人机集群组成Fig.1 Composition of UAV swarm
1.1 无人机集群作战样式
无人机集群作战是无人机集群概念在空天防御作战领域的具体表现形式,无人机集群作战的基础是“集”,关键是“群”,即通过网络聚能的方式发挥作战优势,进而提升战斗力。本文重点针对无人机集群空对地作战样式进行作战构想,在作战过程中主要执行以下几种任务:
1)战场侦察。在复杂的战场环境中,以天基预警卫星、空基预警机和地基雷达获得的多维战场信息为基础,利用无人机集群自身的优势实现对敌方高价值目标的抵近式探测,实现对敌方目标位置的准确定位与跟踪,为后续的作战行动提供有力的数据支撑。
2)通信干扰。无人机集群在执行作战任务过程中会携带电子干扰设备,通过发射不同频段的电磁波干扰地面雷达系统、通信系统等,破坏其通信链路造成敌方武器系统瘫痪,为我方作战力量提供有力保障。
3)火力攻击。在充分掌握敌方武器部署及敌方目标的位置信息后,无人机集群目标将配合其他作战打击力量对敌方重要军事设施及目标进行火力打击。火力打击方式主要有自杀式攻击和无人机载荷攻击两种。
图2给出了无人机集群作战样式。
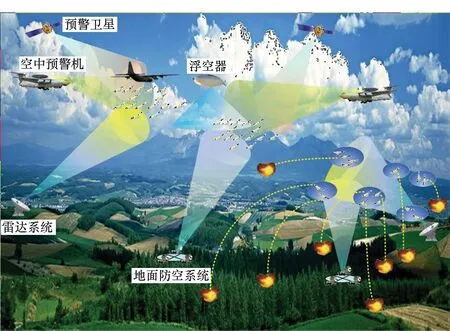
图2 无人机集群作战样式Fig.2 UAV swarm operation style
1.2 无人机集群空对地作战流程
按照无人机集群的概念以及无人机集群空对地作战样式分析,本文将无人机集群空对地作战流程分为挂载飞行阶段、编队飞行阶段和分群攻击三个阶段。
1)挂载飞行阶段。挂载飞行阶段主要是指空中载机挂载无人机飞行的阶段。在这个阶段的主要任务是完成任务层面的工作。
2)编队飞行阶段。编队飞行阶段主要是指空中载机到达指定位置释放无人机后,无人机集群按照一定的编队规则沿着起始规划的航路进行编队飞行的过程。在这个过程中要完成战场侦察任务和通信干扰任务。
3)分群攻击阶段。分群攻击阶段主要是指无人机集群完成战场侦察和通信干扰任务后,我方指控中心对敌方武器配置即目标位置信息进行融合处理确认后,首先确认打击目标的区域,进行作战前的准备,主要对航路和任务参数进行调整,再次确认作战方式后执行分群攻击任务,完成对敌方目标的压制性和毁灭性打击。
不同阶段的作战流程如图3所示。

图3 无人机集群作战流程Fig.3 UAV swarm operation process
2 无人机集群作战过程建模
2.1 无人机集群空对地作战流程连续时间Markov链模型(CTMC模型)
本文研究无人机集群目标飞行作战过程模型时应做如下假设:
1)假设每个飞行阶段之间相互独立。
2)在挂载起飞阶段,主要任务是完成任务层面的工作;编队飞行阶段主要执行战场侦察任务和通信干扰任务;侦察和攻击模式主要集中在分群攻击阶段,即针对攻击目标有无价值采取攻击或侦察模式,且假设攻击时间和搜索时间服从指数分布。
3)建模过程中不考虑作战环境的影响。
4)建模过程中不考虑阶段转化的时间,即假设模型转换时间是瞬时的。
将无人集群目标飞行作战过程看作一个时齐的连续时间Markov链。
设在挂载飞行阶段k,载机平台释放n架无人机,每架无人机有侦察或攻击两种状态,其状态向量为S=[S1,S2,…,Sn],Si=1,0分别表示第i架无人机处于攻击或不处于攻击状态,则系统共有|S|=2n个状态。
假设离散状态空间为E={0,1,2,…,N}或E={0,1,2,…},{X(t),t∈[0,+∞]}是离散状态空间E上的一个随机过程,若对任意自然数,任意n个时刻t1,t2,t3,…,tn(0≤t1 P{X(tn)=in|X(t1)=i1,X(t2)=i2,…,X(tn-1)=in-1} =P{X(tn)=in|X(tn-1)=in-1}, i1,i2,…,in∈E (1) 则称{X(t),t∈[0,+∞]}为离散状态空间E上的连续时间Markov过程。当t,Δt≥0时,P{X(t+Δt)=j|X(t)=i}=Pij(Δt),称其为时齐的连续时间Markov过程。Pij(t)为在t时刻经Δt时间的概率转移函数,表示已知t时刻处于状态i,t经时间Δt后变成状态j的概率。时齐的连续时间Markov过程中的转移概率函数仅和转移出发的状态i、转移所经时间Δt、转移达到的状态j有关,而与转移开始的时刻t无关。 由转移概率全体组成的矩阵成为转移矩阵,记为: 根据条件概率的性质,可以得到转移概率函数如下性质: 1) 0≤Pij(t)≤1,i,j=1,2,… 4) Chapman-Kolmogorov方程: Chapman-Kolmogorov方程的含义为:若经过t+Δt时间状态由i到达状态j,则必须先经t时间状态由i到达状态r,再经过Δt时间由状态r到达状态j。 对于连续时间Markov过程,由于其时间是连续的,所以情况变化之间的时间周期遵循指数分布。同时情况完全可以由它所处的状态来描述,每个状态都可以转换到另一个可行状态。下一个状态的选择是“指数竞赛”的结果,也就是说下一个状态是由最先发生的事件决定的,而下一个事件发生的时间遵循指数分布。 定义qij为Markov过程的速率函数,表达式如下: (2) Markov过程的速率矩阵为矩阵Q,记为: 设随机连续状态有限Markov过程的转移概率函数为Pij(t),速率函数为qij,则 (3) 记矩阵P={Pij(t)},则Kolmogorov方程可记为: (4) Kolmogorov是关于P(t)的线性微分方程组,即CTMC模型的求解为常微分方程组初值问题的求解。 设飞行初始时间为0,则CTMC模型的解为: P(t)=P(0)exp(Q2n×2nt) (5) 基于CTMC模型的无人机集群作战过程建模的主要思路是在无人机集群飞行作战过程的每一个任务阶段分别建立各自的Markov模型,然后从初始阶段开始,逐阶段求出该Markov模型的解。建模过程如下: 1)将多阶段系统分解为若干独立的单阶段系统。将无人机集群执行作战任务的时间段记为[T0,Tn],将该时间段划分为三个时间段,在每个时间段内,tnstart、tnend分别表示阶段n的开始时间和结束时间,由假设条件可知,不考虑转移时间,则t1end=t2start,t2end=t3start,从任务初始时刻T0开始,逐个阶段求解Markov模型中的状态概率向量P(t),将前一个状态的终止状态作为下一个状态的起始状态,即有: P(t1end)=P(t2start) (6) P(t2end)=P(t3start) (7) 2)建立各个单阶段系统的Markov模型。 飞行阶段Ⅰ: (8) 飞行阶段Ⅱ: (9) 飞行阶段Ⅲ: (10) 3)将上一阶段的最终状态转移率作为下一阶段的最初状态转移率处理阶段间的依赖性,从而使各个单阶段的运行时间扩展至整个运行时间,计算作战任务完成的可靠度。 对于每个阶段的Markov模型,状态空间Ω={1,2,…,n}被分为不攻击状态集Ωna和攻击状态集Ωa,定义如下变量: (11) 则在每个阶段结束作战任务完成的可靠性为: Psuccess(t)=Pr{I(u)=1,∀u∈[0,t]} (12) 无人机集群作战建模过程如图4所示。 图4 无人机集群作战过程模型Fig.4 UAV swarm operation process model 由理论分析可知,连续时间Markov链模型的数值求解过程中目前常用的解析求解方法存在求解效率低的情况,本文拟考虑采用四阶Runge-Kutta数值方法求解模型。 经典四阶Runge-Kutta法计算公式如下: (13) 针对连续时间Markov模型,将函数的绝对值换成函数向量范数,四阶Runge-Kutta法计算公式如下: (14) 式中,矩阵Q2n×2n为Markov过程的速率矩阵,Pn为状态概率向量,h为步长,K1、K2、K3、K4为行向量。四阶截断误差为O(h5)。四阶Runge-Kutta法在求解连续时间Markov模型的解的过程中将解析方法求解中矩阵的幂运算转化为矩阵与向量乘积的运算,具有高精度、良好的收敛速度、稳定性和计算步骤的可变性。 四阶Runge-Kutta法算法伪代码如算法1所示。 算法1 四阶Runge-Kutta法算法伪代码 从算法1伪代码中可以看出,Runge-Kutta法计算过程中需要存储四个长度为N的一维数组,且该算法计算过程总耗时为O(N2qt)。Runge-Kutta算法是对微分方程的数值解法,该方法的思想是在积分区间内进行插值,优化总的斜率得到更新结果。因此,其精度应高于直接积分。Runge-Kutta算法的阶数越高,即插入点数越多,计算结果越精确,相应的算法复杂度也越高。四阶Runge-Kutta算法的精度已经能满足大多数精度要求,并且计算复杂度也适宜多数处理器的性能。在利用四阶Runge-Kutta法求模型数值解的过程中,核心问题是对算法中的向量乘法矩阵PnQ2n×2n进行处理,而速率矩阵Q2n×2n中大部分元素为零,非零元素所占比例非常小的大型稀疏矩阵,对这种矩阵的求解需要占据大量的内存空间和计算时间。 由于速率矩阵的稀疏特性,同时在矩阵中非零元素较为分散,为获得较好的压缩效果和求解质量,本文采用基于行压缩存储(compressed row storage, CRS)的四阶Runge-Kutta法在求解得到的预处理结果的基础上继续优化求解效率得到模型的数值解。 行压缩存储策略主要是使用Value、Colind和Rowptr三个数组对稀疏矩阵进存储。 1)Value数组:用于逐行存储矩阵的非零元素的值。 2)Colind数组:用于存储矩阵的非零元素列的索引值。 3)Rowptr数组:用于存储Value数组中每一行第一个非零元素列的索引值。 CRS中Value数组中的元素数据类型为double,由于在该数组中存储非零元素,故其数组长度为nnz,存储空间大小为8nnz;同理分析可知Colind数组长度为nnz,由于数组中数据类型为integer,其存储空间大小为4nnz;Rowptr数组长度为m+1,存储空间为4(m+1),由以上分析可以得到CRS策略的存储空间为8nnz+4(nnz+m+1)。 本文定义压缩率CR来更好地分析不同存储方案的压缩效果,计算公式如下: (15) 其中,Q1为稀疏矩阵中的元素个数,Q2为稀疏矩阵中存储的元素个数。 基于CRS的四阶Runge-Kutta算法的求解过程如图5所示。 图5 算法流程Fig.5 Flow chart of the algorithm 本文假定载机平台中的空中运载机一次性释放15架无人机遂行后续无人机集群作战任务,同时无人机集群作战各个阶段时间分别为t1=10 min,t2=20 min,t3=30 min。 为验证本文所提模型的有效性,采取本文算法与参考文献[13,15,17]所采用模型进行对比,仿真结果如图6所示。 图6 不同模型下的无人机集群完成作战任务可靠性Fig.6 Reliability of UAV swarm completing combat mission under different models 从图6中可以看出,采用本文模型得到的无人机集群完成任务的可靠性为0.991 518 574 339 88 7,采用文献[13,15,17]模型得到的无人机集群完成任务的可靠性分别为0.901 826 413 752 31、0.755 231 275 664 302和0.855 567 893 297 587。从结果中可以看出,采用本文模型无人机集群完成任务的可靠性更高,同时也可以看出,本文模型下的曲线收敛速度和完成任务的时间均优于其他模型。 本文使用基于CRS的四阶Runge-Kutta算法对各阶段的Markov模型逐一求解,求解到最后一个阶段的可靠性即无人机集群完成作战任务可靠性。 4.2.1 本文算法求解完成作战任务可靠性 取步长为0.1、0.01、0.001、0.000 1时采用本文算法得到的无人机集群完成作战任务可靠性分别为0.999 985 963 215 25、0.999 985 975 256 13、0.999 985 975 256 32、0.999 985 975 256 78。可以看出,4个步长均能完成作战任务,可靠性均收敛到小数点后十二位,即完成作战任务的可靠性为0.999 985 975 256。 4.2.2 不同数值算法对求解结果的影响 为验证不同数值求解方法对无人机集群完成作战任务可靠性的解的特点,表1给出了不同步长下采用本文四阶Runge-Kutta算法与Euler法[27]、三阶Runge-Kutta法[28-29]和多步法[30]进行对比实验。 表1 不同数值算法对求解结果的影响Tab.1 Influence of different numerical algorithms on solution results 从表1中可以看出,采用数值方法求解模型时不影响四阶Runge-Kutta预处理的结果精度,但是针对预处理结果是否通过存储空间压缩,会影响后续行压缩存储算法的运行速率,进而影响算法运行时间。同时从表1中也可以看出,针对不同数值求解算法求解预处理结果的运行时间来看,四阶Runge-Kutta算法运行时间最短,其次是多步法、三阶算法和Euler法。 图7给出了采用行分块压缩[21]、列压缩策略[21]和本文基于行压缩存储策略的存储空间对比图。 图7 不同存储策略下的存储空间与压缩率对比图Fig.7 Comparison of storage space and compressed rate under different storage strategies 从图7中可以看出,采用行压缩策略的存储空间为5 021,行分块压缩存储空间为5 876,采用列压缩储存空间最大,同时也可以得到采用行压缩策略的压缩率,即空间占有率低、储存效率高,相比可以得到采用列压缩空间效率最低、压缩率较低。采用行压缩策略空间效率高的原因是由速率矩阵Q决定的,速率矩阵Q中的非零元素并不连续成块,而且非零元素块的长度也不一致,采用其他压缩策略需要更多的辅助数组,导致储存量大、压缩率低、矩阵运算复杂。 表2给出了未压缩和本文基于行压缩存储的四阶Runge-Kutta算法在步长为0.1,0.01,0.001和0.000 1时的算法运行时间对比。 表2 不同压缩算法对算法时间的影响Tab.2 Influence of different storage space compression on algorithm time 由表2结果可知,在采用四阶Runge-Kutta算法求解出模型的预处理结果后,不采用储存空间压缩算法运行的时间在相同步长的情况下约为采用行压缩存储算法运行时间的1 000倍,主要原因为速率矩阵Q215×215为大型稀疏矩阵,其中的零元素占据大部分空间导致算法运行效率低。采用行压缩策略算法的运行时间短于采用其他压缩策略算法的运行时间。 本文针对无人机集群作战的连续时间Markov链模型求解问题,主要工作及创新点如下: 1)在设计作战背景和作战流程的基础上将无人机集群作战过程划分为三个阶段,并分阶段对无人机集群作战的状态转移过程建立CTMC模型,并通过对比实验验证本文模型的有效性和可行性。 2)提出基于行压缩存储四阶Runge-Kutta算法求解Markov模型,将解析方法求解中的矩阵的幂运算转化为矩阵与向量乘积的运算,得到预处理解,并针对预处理解得到矩阵的稀疏特性,采取行压缩存储的方法,提高算法求解效率。 3)为验证不同数值求解方法对无人机集群完成作战任务可靠性的解的特点,将本文算法与Euler法、三阶Runge-Kutta法和多步法进行对比实验。仿真实验表明,无人机集群完成作战任务的可靠性选定步长之后不随求解方法变化而变化。 4)为验证不同压缩测率的压缩效果以及对算法时间的影响,将不同储存压缩策略和本文算法在不同步长情况下算法运行时间进行对比实验。仿真实验表明,不采用储存空间压缩算法运行的时间在相同步长的情况下约为采用行压缩存储算法运行时间的1 000倍。同时采用行压缩策略的压缩率,即空间占有率低,储存效率高。 综上所述,基于行压缩存储四阶Runge-Kutta算法能够较好地解决无人机集群目标作战解析建模时在状态转移过程中存在计算速率低的问题。2.2 基于CTMC模型的无人机集群作战过程建模

3 模型求解

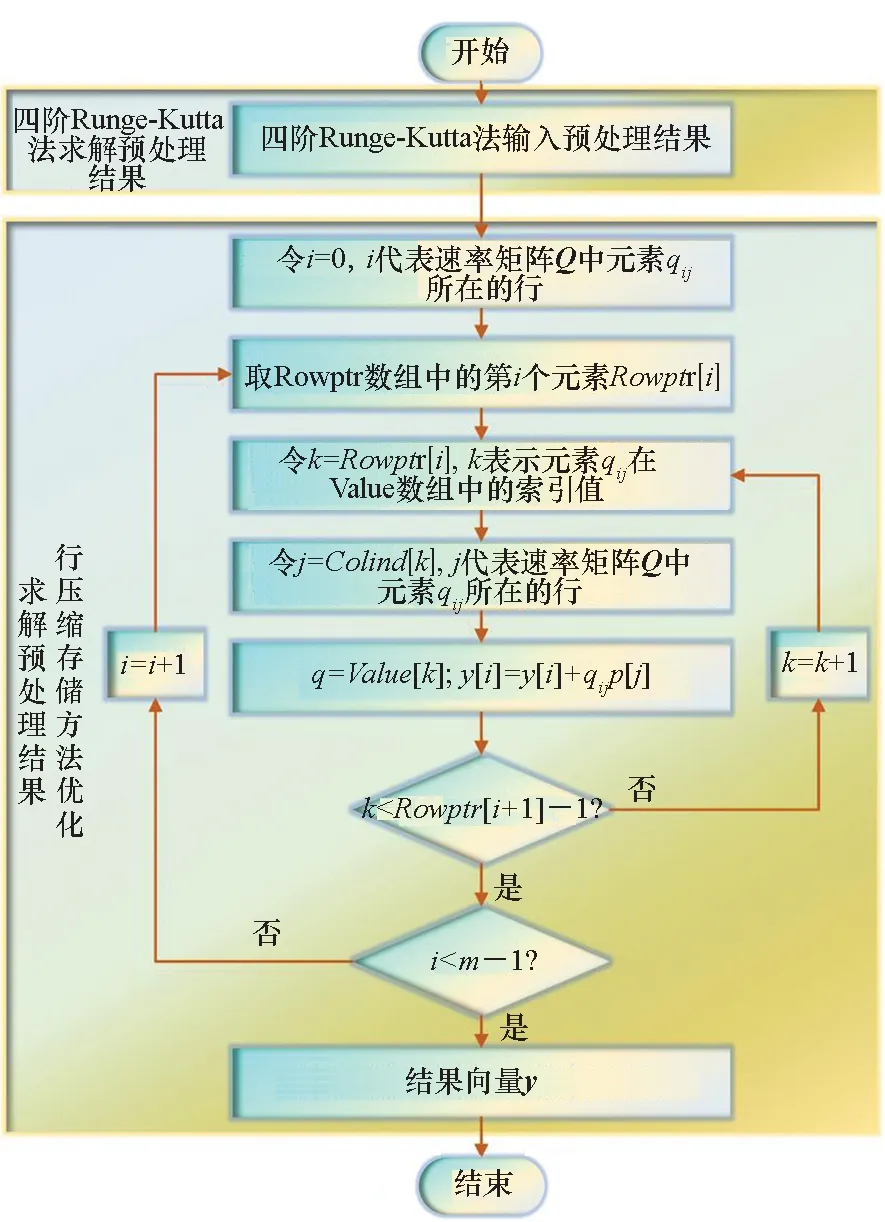
4 仿真验证
4.1 不同模型对无人机集群完成作战任务可靠性的影响
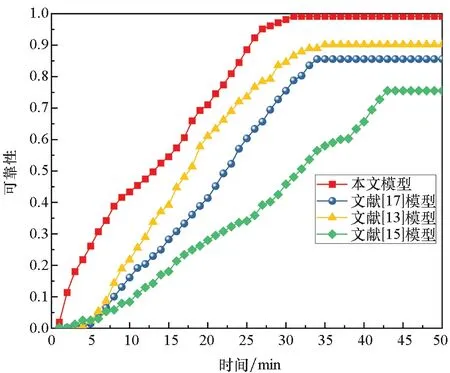
4.2 无人机集群完成作战任务可靠性求解

4.3 不同压缩策略的压缩效果分析

4.4 不同压缩策略对算法时间的影响

5 结论

