采用压缩感知的卫星高频姿态确定方法
汪 璞,胡祥语,安 玮,盛卫东,林再平,曾瑶源
(1. 国防科技大学 电子科学学院, 湖南 长沙 410073; 2. 中国人民解放军93147部队, 四川 绵阳 621000)
高频姿态抖动是卫星姿态确定中的常见误差源。这类高频振动一般会超过常规陀螺和星敏的频率测量范围。所以,当高频姿态抖动存在时,传统组合定姿系统难以精确测定卫星姿态[1-5]。
目前主流的高频姿态抖动测定方法是利用高频姿态传感器对姿态进行测量。这类研究常见于高精度对地观测卫星遥感图像的应用中[6],例如,日本的先进对地观测卫星(advanced land observing satellite, ALOS)基于高采样率的姿态传感器实现了对高频姿态抖动的测量。这类方法关键在于具备高性能的姿态传感器,但高性能姿态传感器通常难以获得。在国内,卫星上常用姿态的测量频率通常低于10 Hz[7]。有一些型号的陀螺能够在较高频率进行测量,但其通常较重且价格昂贵。所以,很有必要研究利用低频陀螺实现高频姿态确定的方法,实现高性价比的姿态测量。
姿态确定方法大致可分为确定性方法和动态滤波估计算法两类。动态滤波估计算法精度普遍更优,是目前工程应用中的主流算法,后文主要针对该类算法进行介绍。动态滤波估计算法的关键在于选择合适的状态变量,根据卫星姿态运动学建立起状态方程,并根据姿态传感器的测量特性,建立起描述状态变量与测量值之间关系的测量方程,通过滤波算法降低误差,得到高精度的定姿结果。目前常用的动态滤波估计算法有:扩展卡尔曼滤波、无迹卡尔曼滤波、非线性预测滤波和粒子滤波等[8]。这些算法各有优势,能在各自的应用领域取得较好的效果,但其都只能在姿态传感器的测量频率范围内进行姿态确定,一旦出现超过姿态传感器测量频率范围的高频姿态,相应算法的姿态确定精度就会下降。
为了能在无高频姿态传感器的条件下实现高频姿态抖动的测量,降低抖动对姿态确定的影响,本文提出了一种使用普通姿态传感器对高频段姿态确定的方法。该方法主要基于压缩感知技术进行实现。卫星的高频姿态抖动由一系列的频率分量组成,而且它们通常在频域稀疏[2]。基于这种稀疏特性,利用压缩感知中的重构算法,可以从低于奈奎斯特采样频率的姿态测量数据中恢复出高频姿态量。
本文所提出的方法包含三个部分:①获取多组低频姿态估计值;②融合估计值;③从融合的估计值中恢复出高频段姿态数据。为了能获取原始的姿态估计值,所提方法使用了一组星敏以及三组具有不同采样频率的陀螺组合测量系统。三个使用星敏和陀螺数据的卡尔曼滤波器被用于估计飞行器的姿态。使用不同的陀螺数据以及相同的星敏数据,每个滤波器均可以产生一组姿态估计值。每组姿态估计值的时间间隔均不相同。根据压缩感知理论,重构算法要求有时间上非均匀分布的测量值作为输入。因此,上述三组非均匀分布的测量值,被融合到一起,用以产生一组非均匀分布测量值。基于融合得到的数据,高频段的姿态数据将被感知并恢复出来。从本文的仿真结果可见,该高频姿态确定算法有效而且稳定。
1 基于间接卡尔曼姿态滤波器的低频姿态确定方法
由陀螺和星敏感器组成的姿态确定系统被广泛应用于具有严苛要求的卫星姿态控制中。陀螺和星敏的测量值通常会配合间接卡尔曼滤波器进行使用[9]。本节介绍了采用基于星敏和陀螺的卡尔曼滤波器进行姿态估计的方法。卡尔曼滤波器的整体结构如图1所示。
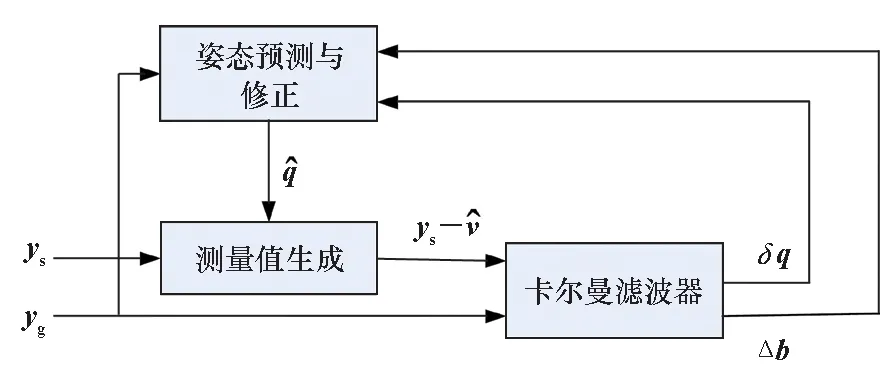
图1 组合定姿卡尔曼滤波器结构Fig.1 Frame of Kalman filter in attitude determination
1.1 四元数与传感器模型
1.1.1 四元数
姿态用四元数进行表示:
(1)
其中,qe=esin(θ/2),q4=cos(θ/2),单位向量e表示卫星旋转轴在某指定姿态参数坐标系(如东南地)中的指向,θ是旋转角度。
基于四元数的卫星转动方程可以表示成如下形式:
(2)

(3)
1.1.2 传感器模型
陀螺输出yg和星敏输出ys定义如下:
(4)

1.2 姿态预测与更新
滤波器的目的是从yg和ys中估计姿态四元数q。在本文中,基于间接卡尔曼滤波器进行估计。首先,利用式(5)进行姿态四元数预测:
(5)

利用式(6)更新q:

(6)
δq并不依赖于ωg(角速度)但依赖于陀螺漂移b以及随机噪声ηg。所以,尽管旋转角度较大,可以假设δq较小而且其可以被近似表示为:
(7)
间接卡尔曼滤波器并不直接估计姿态四元数q,而是对δq进行估计,然后利用δq的估计值,结合姿态传感器的测量值计算得到实际姿态值。
通过对式(5)和式(6)的线性离散化,可以得到:
(8)
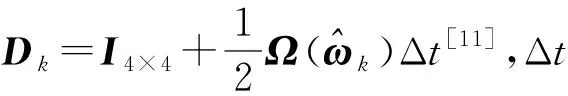
1.3 状态方程
对一个间接卡尔曼滤波器而言,其卫星姿态误差的状态向量可以定义为:
(9)
此状态向量包含六个变量。对卡尔曼滤波器而言,其误差状态方程可以定义为:

(10)
其中:
ηb表示陀螺漂移误差。
为了应用离散时间的卡尔曼滤波器公式,需要将上面的误差预测公式离散化:
Xk=Mk-1Xk-1+Wk
(11)
其中:Mk-1表示状态转移矩阵从时间tk-1向前预测到时间tk,
Mk-1≈I6×6+FΔt
(12)
Δt等于陀螺测量值的采样间隔;Wk是高斯白噪声过程,其均值和方程函数定义为
(13)

1.4 测量方程

(14)
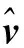
(15)
由于姿态角度差异极小(通常小于60角秒,即≪3×10-4rad),误差矩阵中的高阶项均为可忽略小量,它们可以被近似表示为:
(16)
基于式(16),这些姿态差异角能够通过式(17)与状态方程联系起来:

(17)
通过对式(17)的线性离散化,可以得到:
Zk=HkXk+Vk
(18)
其中,Vk是测量误差且具有如下特性:
(19)
测量矩阵Hk可定义[9]如下:
(20)
1.5 卡尔曼滤波器
标准卡尔曼滤波器的主要步骤如算法1所示[13]。

算法1 卡尔曼滤波器处理步骤
2 压缩感知简介
压缩感知是21世纪初兴起的一种信号复原技术。基于该技术,可以利用远低于奈奎斯特采样率的采样值,精确重构出原始信号[14]。为便于阐述,以如下问题为例来介绍压缩感知中的基本概念。假设需要从一个不完整测量值中,恢复一个N×1维的信号x,该向量的测量值为:
y=Φx
(21)
其中,Φ是一个M×N的测量矩阵,且M≪N;y表示M×1的测量值向量。由于y的维数远远低于x的维数,方程(21)是欠定的,难以实现对信号x的重构。然而,如果原始信号x是K稀疏的(即x中仅有K个元素不为0),则x有可能被精确求解出,其如图2所示。
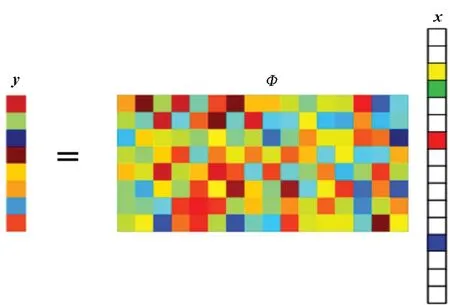
图2 对稀疏信号的线性测量Fig.2 Linear measurement of sparse signal
在图2中,白色方块表示0值,彩色方块表示非0值。在该种情况下,只需确定K个非0元素在x中的位置并针对这K个元素进行求解,而不需要求解x中所有元素的值。这极大地降低了对采样点数量的要求,即便y中元素数量远少于x,也可能准确恢复出x。根据压缩感知理论,当Φ满足约束等距性准则[15]时,则信号x可以由测量值y通过求解最优l0范数问题精确重构:
(22)

但在实际应用中,大部分自然信号都不是稀疏的,在对这类信号进行重构之前,首先需要通过某种变化Ψ进行稀疏表示,通过对其稀疏系数的重构,间接重构出原始信号。考虑一个非稀疏的自然信号f的重构问题,其不完整测量值y=Φf,f可以被稀疏表示,其稀疏表示系数为x,即:
f=Ψx
(23)
具体如图3所示。

图3 信号的稀疏表示Fig.3 Sparse representation of signal
关于信号f的测量方程可以被重写为:

(24)


图4 压缩感知的线性测量Fig.4 Linear measurement in compressive sensing


(25)

在确定压缩感知的测量方程后,剩下的核心问题就是如何从式(24)中求解出x,该求解过程被称为信号重构。在信号重构领域,相关研究人员已提出了一系列的信号重构算法,主要有最小l1范数法、匹配追踪系列算法、迭代阈值法和最小全变分法等。各类方法均有各自特点,需要根据应用环境的不同,选取相应的算法。其中,匹配追踪类算法由于其计算复杂度相对较低,更适宜于二维信号的恢复重构,本文中即采用该类算法[18-19]。
3 高频段姿态确定
高频段姿态确定包含三个主要步骤。首先,利用三个间接卡尔曼滤波器进行姿态估计。由于输入的陀螺数据有不同的采样频率,所以三个滤波器的估计值也具有不同时间间隔。然后,所有滤波器的姿态估计值被融合到一起,用以模拟对初始姿态的非均匀采样。最后,利用压缩感知从融合数据中恢复出高频段姿态数据。受限于计算复杂度,该方法每次仅能恢复出一部分高频姿态数据,如果要完整恢复出全部的姿态,需要反复使用所提方法。本文所提方法的框架如图5所示。
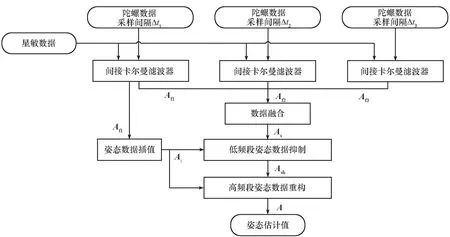
图5 基于压缩感知的滤波方法Fig.5 Scheme of filter based on compressive sensing
3.1 数据融合
为了模拟对平台姿态数据的非均匀性采样,三组数据按照其中各个数据的时间戳点进行了融合。

(26)
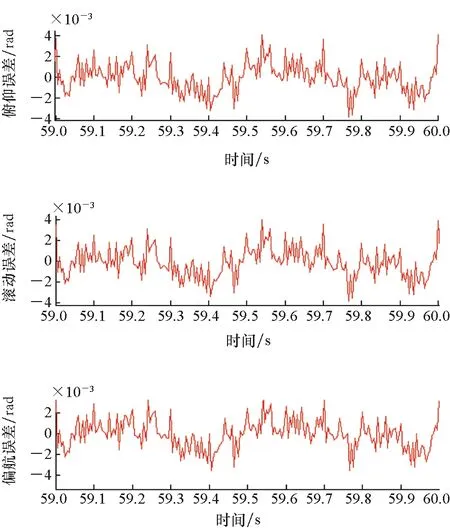
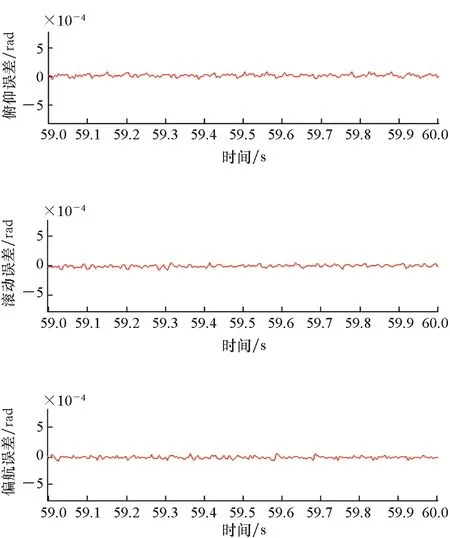
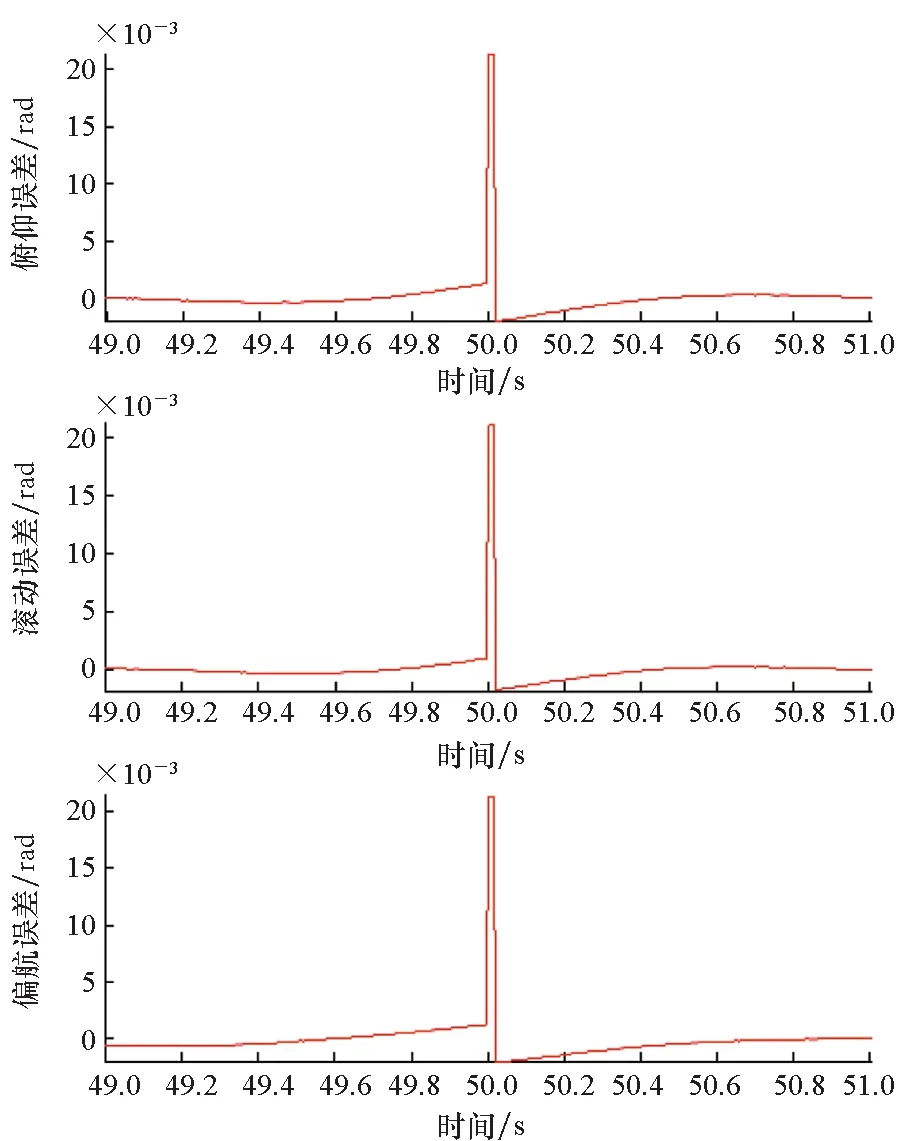
其中,t0,t1,…,tk表示姿态数据的时间戳,并且满足t0 (27) 其中,As表示经过融合后的数据,这个融合后的数据被展示在图6中。 图6 融合数据Fig.6 Merged data As中数据在时间域中非均匀分布。所以,融合数据能被视为一种有效的获取非均匀分布的姿态序列的方法。 高频段姿态Ah的重构可以被看作是压缩感知中一个典型的信号重构问题。它可以被表示为如下形式: Ash=ΦAh+z (28) 其中:Φ是一个k×N的测量矩阵;z是误差项;Ash是Ah的采样集合。 由于Ah在时域不稀疏,所以其并不能直接通过式(28)进行重构,需要被重写为如下形式: Ash=ΦΨxh+z=Θxh+z (29) (30) 目前有大量的稀疏重构算法可供选择。基追踪算法是其中一种常用的信号恢复算法,它能达到较好的精度而且比较稳定。所以,本文使用基追踪算法进行重构。由于稀疏基Ψ和测量矩阵Φ对重构比较重要,下面先介绍一下它们的定义。 1)稀疏基。基于前期的研究[12],航天器的姿态角可以用式(31)进行描述: (31) 其中,A(t)代表了一个轴上的姿态角,Ai表示正弦函数的幅度,φi是正弦函数的相位角,fi表示该函数的频率。 由式(31)可知,A(t)经过傅里叶变换后在频域稀疏。所以,傅里叶基被选为稀疏基,其定义如下: (32) 2)测量矩阵。令Ts表示As中元素所对应的时间,该测量矩阵直接与时间序列Ts相关联。假设Ts=(t0,t1,…,tk),且Δt是三个陀螺采样时间间隔(Δt1,Δt2,Δt3)的最大公约数,通过将Ts除以Δt能够获得一个位置向量Sk。其定义如下所示: (33) 基于Sk,可以获得K个行向量b1,b2,…,bk: (34) 在向量bi中,只有第pi个元素为1,其他所有元素均为0。 然后,该测量矩阵可以被表示为: (35) 为了验证本文所提姿态确定方法的有效性,利用仿真数据对所提算法进行了测试。将其与间接卡尔曼滤波器进行比较测试。为了进一步阐述所提方法的有效性,在不同噪声条件下对该方法进行了测试,并对不同范围下的频率进行了测试。 假设有三组陀螺和一组星敏被安装于一个三轴稳定的卫星之上。每组陀螺采样间隔均不相同,分别为[55 ms(18.2 Hz)85 ms(11.8 Hz)95 ms(10.5 Hz)],三组陀螺的测量时间间隔为5 ms。为简便起见,假设一组之中的三个陀螺平行于飞行器的三轴且其性能均相同。星敏的采样频率设为1 s(1 Hz)。 仿真时间持续了100 s,其仿真的步长为5 ms。 星敏和陀螺的测量数据通过数字仿真获得。陀螺所采用的误差为角度的随机游走误差以及角速率的随机游走误差,其误差率分别为5 μrad/s 和0.5 μrad/s,其中μrad表示微弧度,即百万分之一弧度。三组陀螺有相同的误差参数。星敏的测量误差模型仅包括正态分布的随机误差(15 μrad)。 卫星姿态可以通过式(31)进行描述。假设姿态包括14个频率分量,仿真参数被列在表1中。卫星的高频振动分量通常幅度较小,所以在仿真中将其设为一个小量。 表1 高频段姿态参数Tab.1 Parameters of high frequency attitude 在后续的鲁棒性测试和带宽测试中,部分条件进行了改动。为了测试所提出方法的鲁棒性,调整了陀螺和星敏误差大小,此外还测试了该方法在姿态突变情况下的性能。在带宽测试中,将频率14在20~200 Hz范围内进行了调整。 在本节中,将卡尔曼滤波器与本文所提方法进行了比较。卡尔曼滤波器使用1 Hz的星敏数据和18.2 Hz的陀螺数据。图7展示了真实的姿态角、通过间接卡尔曼滤波器获得的姿态估计值以及本文所提方法获得的姿态估计值。为了更精确地展示各种方法的效果,仅将部分图像放大进行了展示。由图7可知,使用间接卡尔曼滤波器得到的结果中缺乏高频量,而本文所提姿态估计方法得到的结果几乎与真实值一致。 图7 间接卡尔曼滤波器与本文所提方法的比较Fig.7 Comparison between indirect Kalman filter and proposed method 间接卡尔曼滤波器和本文所提方法的三轴姿态估计误差被展示在图8中。为了更清楚地展示两种方法性能,图中只展示了部分结果(59~60 s)。从图8(a)中可以看出,间接卡尔曼滤波器的估计误差主要由高频姿态抖动组成。这类传统的姿态确定方法不能提供高频段的姿态估计信息。间接卡尔曼滤波器估计误差的均值和均方根分别为[0.59×10-5-1.12×10-50.24×10-5]rad和[1.66×10-31.63×10-31.67×10-3]rad。图8(b)显示了基于压缩感知的姿态确定方法的估计误差主要是随机噪声,其中的高频误差量已经被消掉。误差的均值和均方根值分别为[0.76×10-5-1.13×10-50.34×10-5]rad和[2.57×10-52.54×10-56.10×10-5]rad。两种方法的误差均值均为接近0的小量,本文所提方法的误差均方根有明显降低。 通过图7和图8可以发现,本文所提方法可提高对高频姿态量的估计精度。 (a) 间接卡尔曼滤波器(a) Indirect Kalman filter (b) 本文所提方法(b) Proposed method图8 不同方法的估计误差Fig.8 Estimation error of different methods 4.3.1 不同星敏陀螺测量参数 为验证算法的普适性,在4.1节仿真条件的基础上,通过对星敏陀螺测量频率的调整(其他条件不变)重新配置了三组仿真场景,以测试在不同星敏陀螺条件下算法的性能。仿真条件如表2所示。 表2 星敏陀螺仿真参数Tab.2 Parameters of star sensor & gyros simulation 根据表2中设定的星敏陀螺条件,模拟测试了高频定姿算法在这三种条件下的姿态确定精度,得到的结果如表3所示。 表3 不同星敏陀螺测量条件下姿态确定精度Tab.3 Attitude determination precise of different scenes 由以上仿真结果可知,在不同的星敏陀螺测量条件下,高频定姿算法的姿态确定残差依然保持在同一量级,达到较高的姿态确定精度,体现了其良好的普适性。 4.3.2 不同噪声干扰测试 为了展示本文所提方法的可靠性,在不同噪声条件下对本方法进行了测试。在不同的噪声测试中,所有其他的仿真条件都和前面的仿真实验相同,仅对噪声的幅度进行了调整。相应的噪声水平和噪声幅度如表4所示。 表4 噪声水平定义Tab.4 Definition of noise level 本文所提方法是通过姿态估计误差平均值以及均方根误差对方法进行评价的。不同噪声水平下的平均误差和均方根误差如图9所示。 (a) 俯仰角(a) Pitch angle (b) 滚动角(b) Roll angle (c) 偏航角(c) Yaw angle图9 噪声测试结果Fig.9 Result of noise test 在图9中,姿态估计误差的均值在0附近而均方根误差随噪声水平的增长而线性增加。输入误差的微小改变仅仅会导致输出的微小改变,所以可以认为本文所提的方法是稳定的。 4.3.3 姿态突变测试 在实际应用中,有时会出现姿态突变情况,姿态会在一个很短的时间内出现剧烈变化。由于这种姿态突变在频域中并不稀疏,其将会影响姿态重构的精度。所以,很有必要测试本文所提算法在出现姿态突变时的效果。 在该测试中,除添加了一次姿态突变以外,所有的仿真条件都和第一次仿真测试相同。姿态突变发生在50 s左右,其幅度被设为0.02 rad。 姿态突变条件下,间接卡尔曼滤波器和本文所提方法的三轴姿态估计值如图10所示,估计误差如图11所示。 图10 姿态突变条件下估计值Fig.10 Estimation result in attitude jump 图11展示了在突变存在的情况下,本文所提方法的估计误差出现了剧烈变化,但是这些误差很快消退,而且这些估计误差小于间接卡尔曼滤波器。尽管突变会影响本文所提算法的效能,但是该方法能够很快恢复。 (a) 间接卡尔曼滤波器(a) Indirect Kalman filter (b) 本文所提方法(b) Proposed method图11 姿态突变条件下估计误差Fig.11 Estimation error in attitude jump 为了确定文中所提姿态确定算法的带宽,该方法被用以测试不同的高频分量。高频姿态抖动主要是由卫星通信天线、反射镜转动以及动量轮旋转等引起。这些因素引起的误差振动通常小于200 Hz,而在本方法中使用的最高陀螺频率接近20 Hz,所以将测试的高频范围限定在20~200 Hz。其他仿真条件与第一次仿真相同,只有频率分量14在20~200 Hz之间进行了调整,每次的调整步长为1 Hz。 不同高频分量所对应的姿态估计误差的均值以及均方误差被展示在图12中。 随着频率增加,姿态估计误差的均值和均方误差值都无明显变化。实验中均方误差通常在10 μrad以下,在最坏的情况中,均方误差也是在20 μrad附近。图12展示了所提出方法在20~200 Hz范围内能够对超出姿态传感器测量范围的姿态进行确定。姿态采样频率小于20 Hz时,由于在姿态传感器的测量范围内,必然可以被测量到,所以未做相应测试。 (a) 俯仰角(a) Pitch angle (b) 滚动角(b) Roll angle (c) 偏航角(c) Yaw angle图12 在不同频率的测试误差Fig.12 Estimation error at different frequency 本文提出了一种新的姿态确定方法。该方法仅用普通采样频率的姿态传感器就可实现航天器高频姿态估计,且能达到较高精度。该方法利用了航天器高频姿态量在频域的稀疏性,通过压缩感知技术,可以从低频的姿态测量数据中恢复出卫星高频姿态数据。通过仿真结果可以发现,该方法能够测量出高频姿态,并且对误差具有较好的鲁棒性。此外,通过增加姿态传感器,改进重构算法,可以进一步改善高频姿态测量的精度。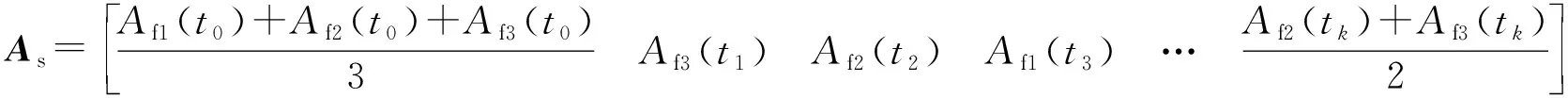
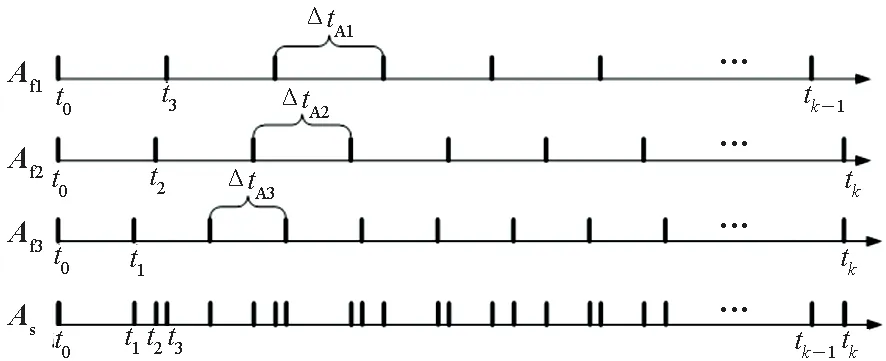
3.2 高频姿态数据重构

4 仿真实验测试
4.1 仿真条件

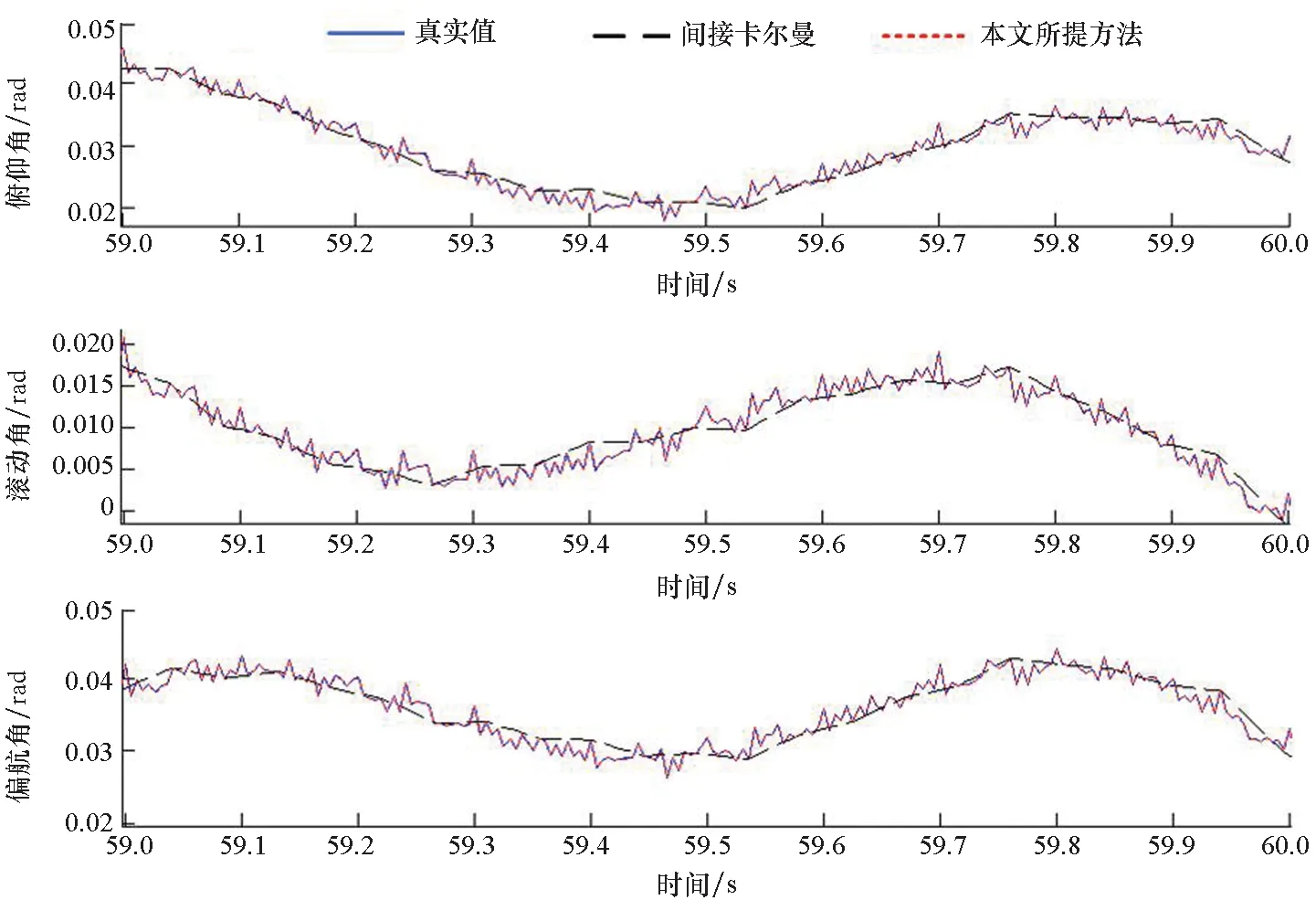
4.2 与间接卡尔曼滤波器的比较
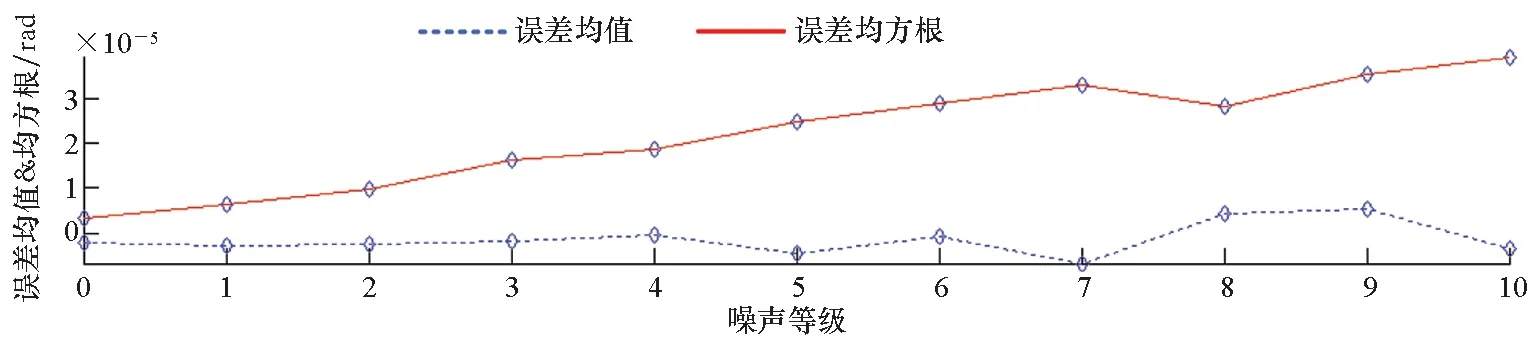
4.3 鲁棒性测试






4.4 带宽测试



5 结论

