低碳经济下考虑满意度的冷链路径优化

魏子秋，林艳敏，李明芳，白士煜

(河北科技大学经济管理学院，河北石家庄 050018)

低碳经济是指使用新技术、制度和产业创新来减少进入生物圈的碳排放。这种低碳特性包括低能耗、低碳排放、低污染和环境友好等[1]。根据国务院《关于印发2030年前碳达峰行动方案的通知》(以下简称“通知”)，到2030年之前社会经济绿色化发展取得显著成果，耗能行业的能源利用率达到国际先进水平。到2025年，非化石能源消耗比例上升至20%，生产总值能源消耗比2020年降低13.5%，顺利实现2030年前碳达峰目标成为中国当下急迫而艰巨的任务。为完成上述目标，“通知”提出了“碳达峰十大行动”，其中交通运输绿色低碳行为被广泛关注。“通知”提出运输工具装备低碳转型、建设高效绿色运输系统和建设绿色交通运输基础设施等建设目标[2]。

最近几年，中国物流业处于快速发展期，冷链物流已逐渐成为行业热点，冷链物流市场的需求和规模正在呈现大幅增长的趋势。2021年末国务院正式印发《“十四五”冷链物流发展规划》，冷链物流被提到国家战略层面[3]。根据 《2021年中国冷链产业发展现状研究报告》，2021年冷链物流行业市场规模预计比2020年增长15.01%，达到4 117亿元，预计未来几年中国冷链物流行业市场主体规模还将不断壮大[4]。碳税也叫环境税，是对二氧化碳排放所收取的税，希望以保护环境为目的，通过削减二氧化碳排放来减缓全球变暖，减少化石燃料消耗和二氧化碳排放。而根据相关报告显示，车辆运输在物流活动中的碳排放是温室气体的主要来源之一，尤其是冷链物流运输中所使用的冷藏车辆所排放的尾气以及制冷所产生的CO2气体[5]。如果冷链物流配送过程的碳排放可以得到有效控制，这对于低碳物流的推进有着重要的意义[6]。因此带有碳排放约束的冷链物流路径规划问题的研究，成为物流行业内的研究热点之一。

车辆路径问题(vehicle routing problem，VRP)最早于1959年由DANTZIG和RAMSER首次提出[7]。HSIAO等[8]对VRP进行了扩展研究，提出最后一英里的新鲜水果和蔬菜交付问题，提供了带有时间窗的VRP，设计了解决方案的编码、适应度函数和进化算子来处理复杂问题。施文嘉等[9]充分考虑生鲜食品的易腐性特质及其在配送过程中的能源成本和货损成本,结合软时间窗及车辆载荷等约束条件,采用免疫优化算法进行路径求解，从而使其所设计的成本控制方法更具有效性。随后方文婷等[10]对其算法进行优化，以总成本最低为研究目标，建立冷链物流路径优化数学模型，将启发式搜索与蚁群算法相结合来解决此类问题。

低碳车辆路径问题(low-carbon vehicle routing problem，LCVRP)是对传统车辆路径优化问题的拓展，添加了碳排放的约束条件，但这同样也是一个NP-hard问题，很难获得全局最优解，因此一般研究运用启发式算法来得到较为合理的优化解[11]。马秋卓等[12]考虑行驶车辆载重的变化以及油耗对碳排放量的影响，结合企业数据为市区小范围的路线规划提供了最优VRP决策。此外，任腾等[13]在考虑顾客满意度和时间窗的基础之上，以碳排放量最小为目标构建冷链路径优化模型，利用改进的蚁群算法能够有效地求解最优成本。随后张旭等[14]在研究多式联运路径优化问题时，在需求与碳交易价格都不确定的情况下，运用混合鲁棒随机优化模型，设计改进的遗传算法进行求解，并进行一定的检验，结果显示在运输效率有效提高的同时可以降低碳排放成本。

综上所述，先前的研究未在优化过程中同时考虑顾客满意度和碳排放成本，传统的冷链物流路径优化只考虑单一的成本，而对于考虑满意度的低碳冷链路径优化问题的研究，不仅需要考虑行驶速度、车辆载重、以及行驶距离等影响因素，还需要根据冷链物流运输的特点，考虑顾客满意度以及碳排放等成本。本研究以顾客满意度较高、车辆碳排放量较少、实现总成本最低为目标建立模型，利用遗传算法对目标模型进行模拟求解。

1 冷链物流路径优化模型构建

1.1 模型假设条件

建立冷链物流配送路径优化模型要从实际情况出发，同时所构建的优化模型要与实际配送环境相结合。然而如果考虑现实中的所有条件，不仅模型求解的难度会大大增加，而且求解所需要的时间也会延长[15]。因此考虑在与实际环境不相违背的情况下，基于一定的假设条件构建合理的优化模型。

针对冷链物流配送现状，假设条件如表1所示。

表1 假设条件

1.2 模型构建

1.2.1 总成本分析

冷链路径优化模型以总成本最低、顾客满意度较高以及碳排放较少为目标，同时根据冷链配送的特有属性，包括以下6部分成本，即：固定成本、运输成本、制冷成本、碳排放成本、损坏成本以及时间窗成本。

1)固定成本

式(1)为固定成本，包括车辆在故障或故障期间的损失，以及司机的工资。车辆发生故障或故障期间的损失，可以根据历史成本进行估算，该项成本与车辆行驶总距离无关。

(1)

2)运输成本

式(2)为运输成本，表示冷链运输过程中的燃料消耗所产生的成本，其成本主要与距离有关，随着距离的增加而增加。

(2)

3)制冷成本

式(3)为制冷成本，表示在冷链运输过程中被消耗制冷剂的费用。式(4)中的C31是发生在运输过程中的制冷成本，式(5)中的C32是发生在卸载过程中制冷成本。

C3=C31+C32，

(3)

(4)

(5)

4)碳排放成本

碳排放成本，表示在配送过程中CO2排放的成本。这包括冷链物流运输中能源和制冷剂消耗产生的碳排放成本。

式(6)为碳排放成本，单位油耗与车辆的负载和距离有关，ZHANG等[16]提出计算公式为Eij(见式(7))。成本C41(式(8))通过运行车辆的行驶距离求出，以及成本C42(式(9))通过制冷设备的时间以及装载量计算。

C4=C41+C42，

(6)

(7)

式(7)中：Em是车辆满载时的单位距离燃油消耗量；E0是车辆空载时的单位距离燃油消耗量；QM是车辆的最大装载量；qij是由i到j的运输量。

(8)

(9)

式中：pc是单位碳税；e是CO2的排放系数；E1为制冷设备单位质量和时间的消耗。

5)损坏成本

式(10)为损坏成本，损坏成本包括由于交货时间增加或卸货过程中环境温度突然变化而造成损坏的冷链货物成本。将传统的TTT(time-temperature-tolerance)理论与冷链物流配送的具体情况相结合，更能与真实数据相匹配。冷链货物的损坏成本表现为随时间指数变动，式(11)中的C51是在冷链运输中因交货时间所产生的损失成本，式(12)中的C52是在装卸搬运卸载过程中的损失成本。

C5=C51+C52，

(10)

(11)

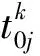
(12)

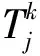
6)时间窗成本

式(13)和式(14)为时间窗成本，即罚款成本，是冷藏车辆无法满足需求点时间窗而产生的额外费用，包括冷藏车辆提前到达需求点的等待成本，以及车辆延迟到达的成本。

(13)

(14)

为了更好的服务，客户对配送时间提出一定要求，此项C6成本虽然在配送总成本中占比很少，但是会影响客户服务的满意度，如果客户服务满意度很低，甚至会失去客户，所以配送过程要尽量在时间窗的范围之内进行配送。其中：W表示一个较为大的损失常数，ω1和ω2分别表示提前到达和延迟到达的惩罚系数，EETj为需求点j可接受的最早到达时间，LLTj为需求点j可接受的最晚到达时间，ETj和LTj为需求点j的最佳时间窗范围。

综上所述，式(15)为总成本的目标函数：

minZ=C1+C2+C3+C4+C5+C6。

(15)

1.2.2 顾客满意度函数分析

顾客满意度是指随着时间的推移，顾客对配送服务的满意程度，这一指标能够充分反映出企业的物流水平[17]。当货物在规定的时间范围内(ETj,LTj)交付到需求点时，那么顾客满意度最高为100%。当配送时间未在需求点要求的时间范围内交付，但仍在需求点可接受的时间范围内(即产品交付到需求点的时间略早或晚于所需时间范围)接收货物，但顾客满意度会降低，具体与提前到达或延迟到达时间与所需的交货时间成正比。当配送服务时间在可允许的最大服务时间范围(EETj,LLTj)之外时，满意度也不会为零，而是在一个可接受的满意度范围，其平均值为 0.6。将顾客满意度函数设定为连续的线性函数，在此基础上，不同时间段的顾客满意度可用模糊隶属函数来表示，如式(16)所示：

(16)

1.2.3 模型约束条件

同时，在实际运算过程中还需要满足以下约束条件：

(17)

(18)

(19)

(20)

(21)

(22)

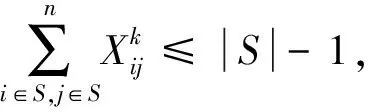
(23)

(24)

(25)

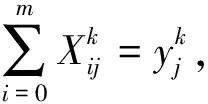
(26)

式(17)表示每辆配送车辆的装载量小于最大装载量；式(18)表示每辆配送车辆到达需求点j的时间窗要求；式(19)表示每辆配送车辆从配送中心出发最终返回配送中心；式(20)表示配送中心有m辆冷藏车，每个需求点j都只能被一辆配送车辆服务；式(21)表示配送中心有n个需求点；式(22)表示所有需求点被服务的车辆总数要不多于总数m；式(23)表示每辆车的行驶路线没有子回路；式(24)表示顾客满意度约束，限制顾客满意度为0.6～1；式(25)表示车辆的行驶方向与配送开始起点和到达服务的唯一性；式(26)表示决策变量的对应关系。

2 算法介绍

2.1 遗传算法及其基本思想

遗传算法(genetic algorithm,GA)是由美国的John Holland教授在1975年首先提出[18]，从生物体的进化中获得的思想，是一种随机搜索方法。该算法利用自然现象进行建模，包括遗传生物进化和达尔文适者生存，即使问题很复杂或未提供其他信息，也可以稳定地搜索最佳解。

遗传算法为复杂问题找到了一个好的解决方案，特别是当其他搜索都未能找到最优解时。遗传算法是随机搜索中解决不明确和复杂问题的关键技术，这些问题需要很大的时间空间才能得到最优解。这是寻找可用于特定设计的解决方案集的完美选择的重要技术。当考虑各种环境载荷时，解决问题时会遇到缺乏高级信息、功能限制和搜索空间大等困难。因此，遗传算法适用于搜索优化路径并找到有效的解决方案。

遗传算法可以定义为一个迭代过程，它维护一组结构，这些结构是候选解决方案。每个候选解称为染色体，染色体可以复制，在每个时间增量(称为一代)中，当前群体中的结构被评定为域解的有效性，并且基于这些评估，使用特定的“遗传算子”形成新的候选解群体，这些算子被大多数遗传算法使用，例如选择、交叉和突变[19]。在遗传算法中主要是交叉，其概率为80%～100%。相比之下，突变是一个从属的关系，这种变化发生在 1%～20%的低概率时[20]。

2.2 算法设计

2.2.1 染色体编码

进行染色体编码时，配送中心需要通过车辆向多个需求点进行配送，每辆车的线路选择情况转化为染色体集合，每条染色体都表示着不同的行驶路径方案。因此运用自然数来进行编码，以提高求解的效率，通过适应度评价和遗传操作，进而选出较优的配送线路方案。如染色体312321表示车辆1为2和6需求点配送，车辆2为3和5需求点配送，以及车辆3为1和4需求点配送。

2.2.2 初始种群

初始种群是由规模不同的个体组成，经过适应度的计算、选择、 交叉、变异等一系列操作生成新的群体，而后不断进行迭代操作，直到达到既定的终止条件。一般为了保证算法求得解的均匀合理，将随机生成初始种群，避免陷入局部最优解问题。

2.2.3 遗传操作

1)选择算子 选择操作是以适应度的大小为依据判断个体能否进入下一代，即种群基因的优胜劣汰。这是为了让更好的个体进入下一代，淘汰适应度差的个体。本研究运用最大保留策略与轮盘赌策略相结合的方法。

2)交叉操作 交叉操作是生成新染色的主要途径，通过将2条染色体的部分基因互换来生成新的染色体，参加交叉的染色体由交叉概率来确定。

3)变异操作 变异操作是为了增加算法的搜索空间，改变部分染色体的基因从而产生新的染色体，通过设定的变异概率进行选择个体。本研究采用随机选择基因位点变异。

2.2.4 适应度函数处理

适应度用来表示染色体的生存概率，运用适应度函数可以求得每一代种群中染色体的生存概率，从而根据概率对每条染色体进行比较和选择。本研究的目标函数为总配送成本最低，因而，以总成本的倒数(即1/minZ)作为适应度函数。

2.2.5 终止条件

当整个流程的迭代次数或者适应度达到设定值时，即可得到当前最优染色体，进而规划出最优的配送路线。

2.3 遗传算法与模型相结合

遗传算法在车辆配送模型中的应用，如图1所示：

1)设定交叉和变异概率、规模大小、迭代次数等参数；

2)遗传算法的染色体编码采用按自然数编码的方式，完成单次运输任务返回配送中心的路径；

3)进行选择、交叉和变异，计算出具备闭合回路的运输路径；

4)根据约束条件和目标函数计算每条路径的适应度；

5)根据各路径的适应度寻找最佳运输路径；

6)根据适应度以及迭代次数的设定，输出最优的配送方案。

图1 迭代流程图Fig.1 Iterative flow chart

3 仿真实验

3.1 实例介绍

基于G冷链物流公司现实运行的情况，仿真一组数据进行模型验证。假设现有一个冷链配送中心和32个配送点，已知所有配送点的位置、配送点需求、配送点的服务时间，以及可接受的最早时间窗和可接受的最晚时间窗，具体统计数据如表2所示。每辆车装载货物后，以配送中心为初始出发点，最后车辆需全部返回配送中心。编号0代表配送中心的信息，编号1～32代表配送点的信息，其位置信息是根据配送点的相对位置换算求得。配送中心有15辆载重为2.5 t的冷藏车辆，冷藏车辆的油耗成本、行驶速度、车辆使用成本等都可以进行统计。

表2 配送中心及配送点信息

3.2 实例求解

使用MATLAB R2021b软件工具编程实现遗传算法的求解，根据该模型实际情况分析，其中的相关参数设定如下(包括采集的实际数据以及模型基础假设数据)：Fk为250元，Qm为2.5 t，P0为3元/km，V为50 km/h，P2为5元/kg，a1为0.03，E0为百公里12.2 L，a2为0.06，Em为百公里38.8 L，P11为5元/h，E1为0.25 L/h，P12为10元/h，e为2.61 kg/L，Pc为0.138元/L，ω1为15元/h，ω2为20元/h，种群大小为200，迭代次数为2 000，交叉概率为0.8，变异概率为0.2；代入配送中心的基础数据和模型参数数据，再结合需求点生鲜品需求量和软时间窗约束，对以下3种不同的目标进行多次求解。

1)目标1

考虑到顾客满意度以及碳排放成本较低，实现总成本最低的路线优化，即C1+C2+C3+C4+C5+C6成本最低。

2)目标2

以不考虑满意度为目标的路线优化，即C1+C2+C3+C4+C5成本最低，以此分析不考虑满意度对各项成本变化的影响。

3)目标3

仅以总的碳排放相关成本最低为目标的路线优化，即C3成本最低。

3.3 对比分析

通过对32个配送需求点的多次模拟求解，求得多次稳定的平均值，如表3所示。不难发现：在考虑顾客满意度以及碳排放成本的前提之下，经过带有软时间窗约束条件遗传算法的优化，冷链配送方案在保证尽量较少延迟送货的前提下，求得最小目标函数为3 414.6元，使用7辆2.5 t的冷链运输车辆，所有服务车辆的碳排放成本为81.3元，路线长度为366.6 km，顾客满意度为74.04%，其顾客满意度达到较优而非最优的水平，表明模型没有为了追求满意度最高而放弃成本优化。

经过比较可以发现，在以不考虑满意度的路径优化为目标时，车辆行驶总距离为343.1 km。虽然配送距离较总成本最低时减少了23.5 km，车辆使用数量未变，但碳排放相关成本提升3.6%，损坏成本提升12%，时间窗成本增加107.1元，满意度下降4.98%，配送总成本提升2.72%。在以其成本最低为目标时，模型虽对总成本进行优化，却较少对时间窗成本进行优化，从而一定程度上忽略顾客满意度的重要性。在以碳排放成本最低为目标时，车辆的使用数目为9 辆，碳排放成本为74元，较另外2种方案可以实现低碳的目标，虽然顾客总体满意度较高，货损成本较低，但配送总成本提升得更多。

表3 结果分析表

4 结 语

低碳经济是高能耗领域尤其是冷链物流产业可持续发展的重要方向，低温配送是冷链物流走向低碳经济的关键环节，基于顾客满意度和碳排放成本的路径优化研究是使冷链物流低温配送过程低碳经济的必然途径。

1)本研究在测量车辆碳排放时，充分考虑车辆负载、行驶速度、行驶距离、道路状况等多重影响因素，使其更加符合实际情况。与现有文献相比，将制冷成本、碳排放成本和损坏成本更加全面和细化，对于相关研究有一定的补充作用。

2)将目标1方案与另外2种方案进行数据对比分析可知，前者仅在配送总费用、配送里程方面达到较优水平，还能提高顾客满意度，提高服务的总体水平。这种求解方式能够实现合理的路径规划，在保证物流服务质量的同时最大限度地减少了碳排放量和总成本，证实了算法及模型的有效性。

总之，本研究为冷链物流配送方案的设计提供了新的思路，但是依然存在不足，主要采用传统的遗传算法进行求解，未来可以考虑对遗传算法进一步改良后进行求解，使其应用于更多的现实场景。