基于DLNS-DSVDD的故障检测方法
谢彦红,张浩然,张 成,李 元
(1.沈阳化工大学理学院,辽宁沈阳 110142;2.沈阳化工大学信息工程学院,辽宁沈阳 110142)
随着现代工业过程的快速发展,企业对系统安全提出了更高的要求。为保证系统的正常运行和设备的可靠运转,过程监控方法应运而生。其中,基于数据的过程监控方法可以从大量数据中提取过程信息,被广泛用于工业过程故障诊断领域[1-3]。
主成分分析(principle component analysis,PCA)[4-5]及其衍生方法,例如核主成分分析(kernel PCA,KPCA)[6-7]、动态主成分分析(dynamic PCA,DPCA)[8-9]和概率主成分分析(probabilistic PCA,PPCA)[10]方法,作为经典的过程监控方法,在石油化工行业得到了广泛应用并取得了令人满意的效果。但基于PCA的故障检测方法通常要求数据服从高斯分布,而大多数过程数据不能满足这个要求,因此上述方法有较高的误报率[11-12]。针对非高斯数据的过程监控问题,TAX等[13]提出了支持向量数据描述(support vector data description,SVDD)方法。该方法通过在特征空间中构建最优超球体进行故障检测,已成功应用于冷水机组[14]和模拟电路[15]等领域。尽管SVDD方法在非高斯故障检测领域取得了显著的成果,但是对多模态动态过程的检测效果有所降低[16]。针对过程数据的多模态特征,HE等[17]提出了FD-kNN(Fault detection using k nearest neighbor)的故障检测方法,该方法通过计算样本间的局部信息消除了多模态结构对故障检测的影响,并取得了较好的效果。但当各模态协方差结构特征差异较大时,FD-kNN方法无法准确地检测出故障[18]。ZHAO等[19]提出了WLS-SVDD(weighted local standardization SVDD)的故障检测方法,该方法利用WLS克服了各模态协方差结构差异的影响,简化了SVDD方法建模和监控过程,提升了故障检测性能。但是模态之间存在的故障样本会降低了WLS-SVDD方法的检测性能。冯立伟等[20]提出DLNS-PCA(double local neighborhood standardization and principal component analysis)的故障检测方法,该方法不仅克服了各模态协方差结构差异的影响,还将模态间的故障样本与正常样本进行了有效地分离,较大地提升了DLNS-PCA方法对多模态特征数据的检测效果。但DLNS方法并未考虑样本间序列相关性对故障检测的影响,若某个模态具有动态特征时,检测性能明显降低。针对过程数据的动态特征,KU等[9]提出了DPCA的故障检测方法,该方法对原始数据矩阵进行扩展,构造动态增广矩阵,将样本间的相关性转换为变量间的相关性,从而提高了对动态过程的检测性能。但是动态增广矩阵存在的冗余信息会增加DPCA方法的计算复杂度。GUO等[21]通过引入慢特征分析(slow feature analysis,SFA)方法提取原始数据的动态信息,有效识别了原始数据的异常变化,郭金玉等[22]提出了DW-ICA-SVM的故障检测方法,有效提取了变量间的非高斯特征并且降低了变量间自相关性对故障检测的影响,上述方法均提升了对动态过程数据的检测性能,但是都未考虑到数据多模态特征对检测性能的影响。
实际工业过程数据大多同时具有多模态特征和动态特征,若仅考虑到了数据单一的特征,没有对数据进行多方位分析,则会出现较多的误报和漏报现象。针对SVDD方法对多模态动态过程故障检测率低的问题,本文提出DLNS-DSVDD(dynamic SVDD based on double local neighborhood standardization)方法。
1 基础方法
1.1 支持向量数据描述
假设一组训练数据集X={x1,…,xi,…,xn}T,其中xi∈Rm,n为样本个数,m为测量变量数,则SVDD方法的原始优化问题可表述为
(1)
式中:a和R分别是超球体球心和半径;C是惩罚因子;松弛变量εi用于确定超球体之外离群点的个数。
通过引入拉格朗日乘数α={α1,…,αi,…,αn}T,并用核函数K(xi,xj)代替样本的内积运算〈Φ(xi),Φ(xj)〉,式(1)的对偶问题可表述为
(2)
(3)
对于一个测试样本点z,其在特征空间中到球心的距离可由式(4)计算:

(4)
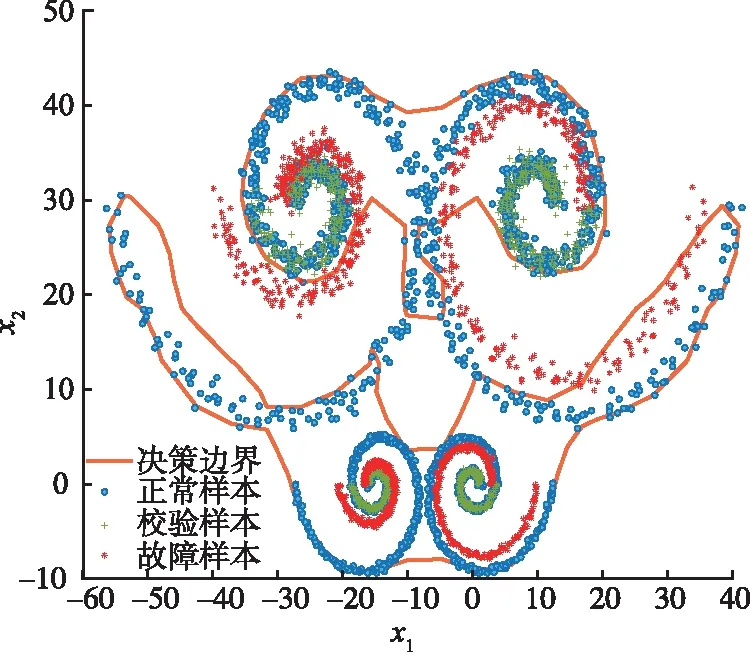
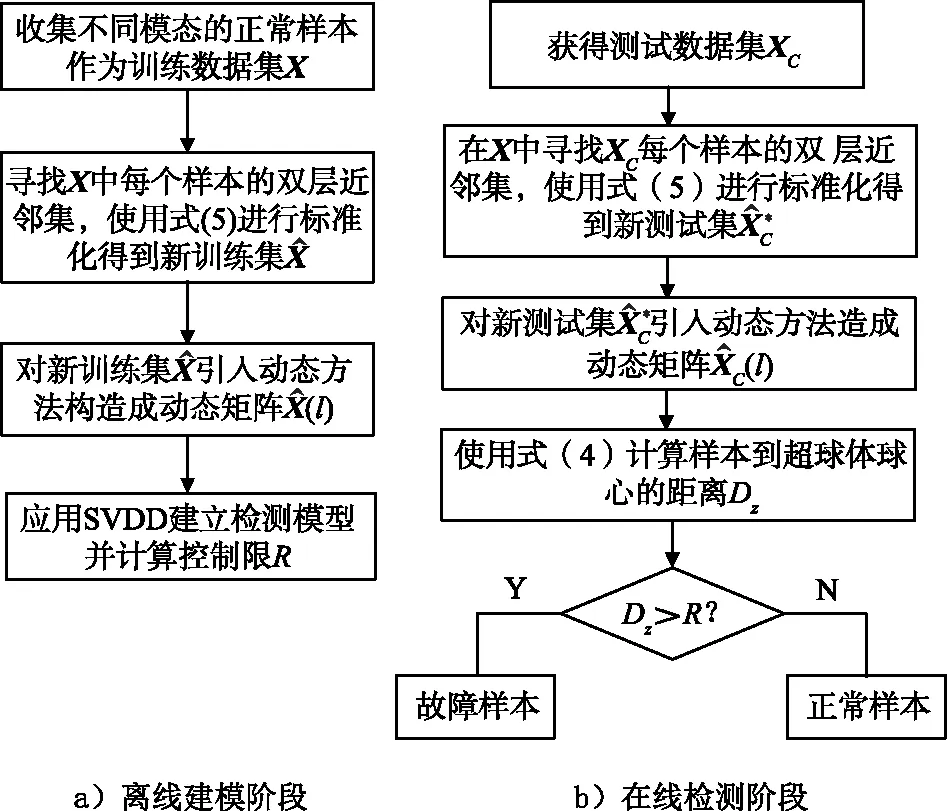
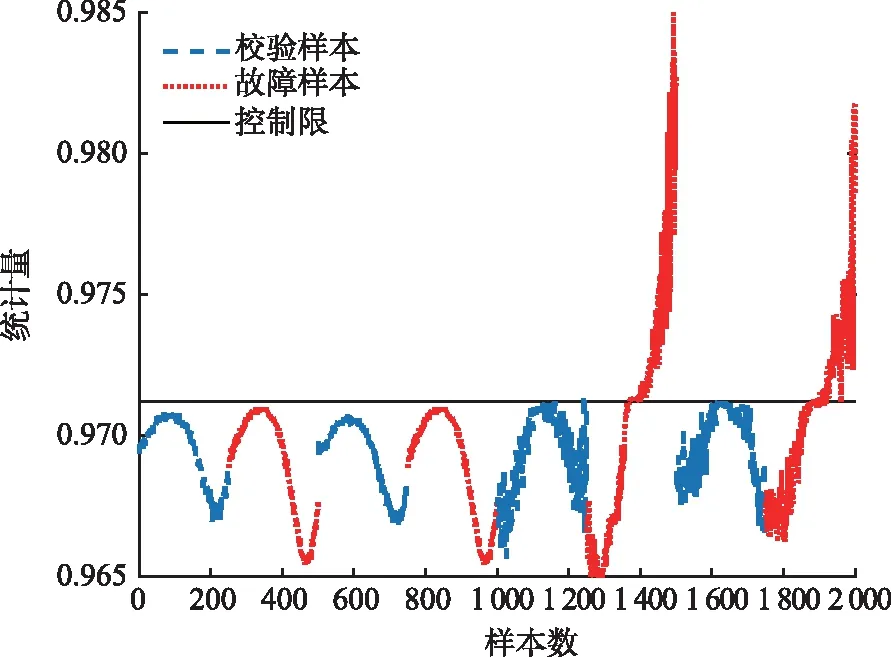
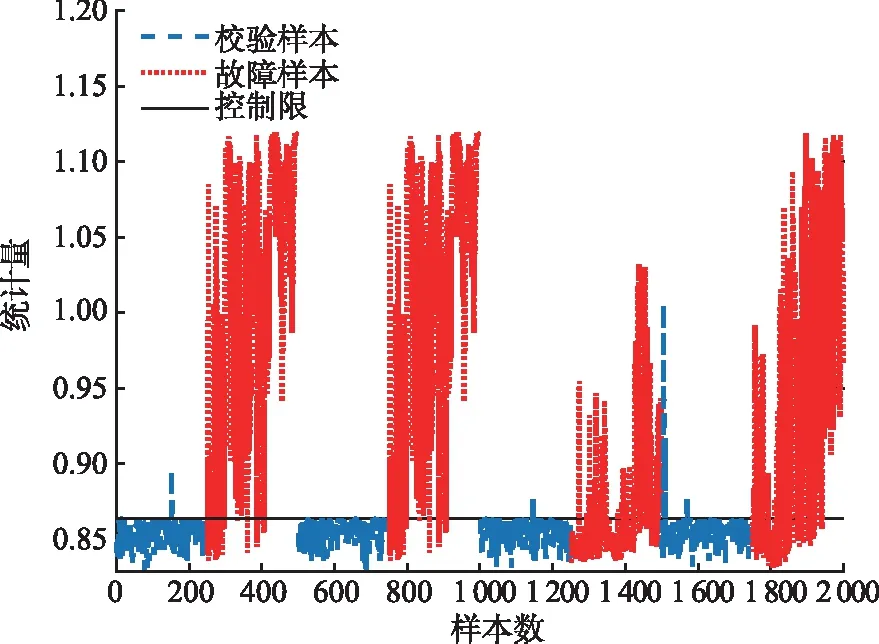
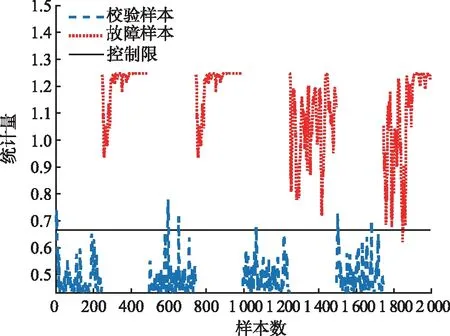
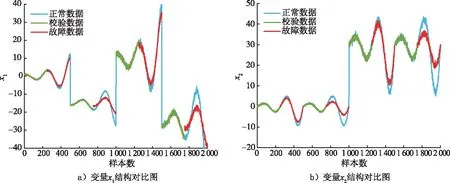
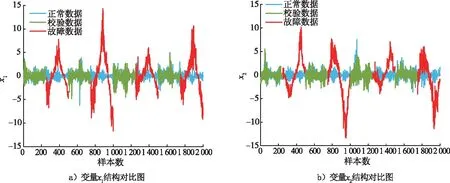
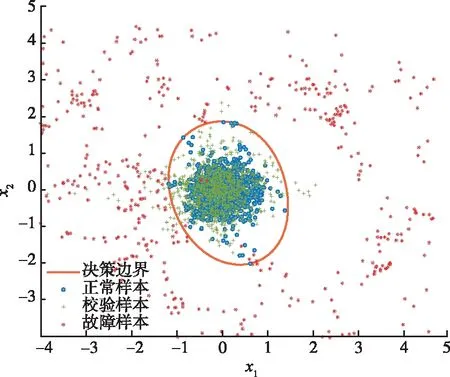
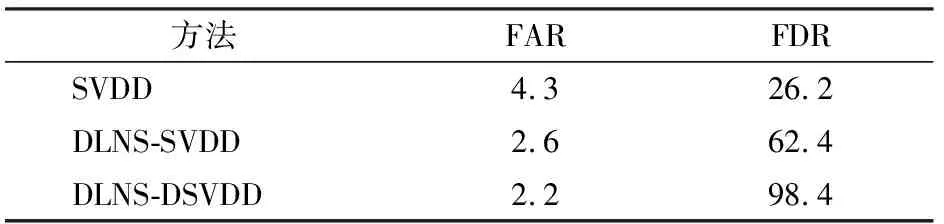
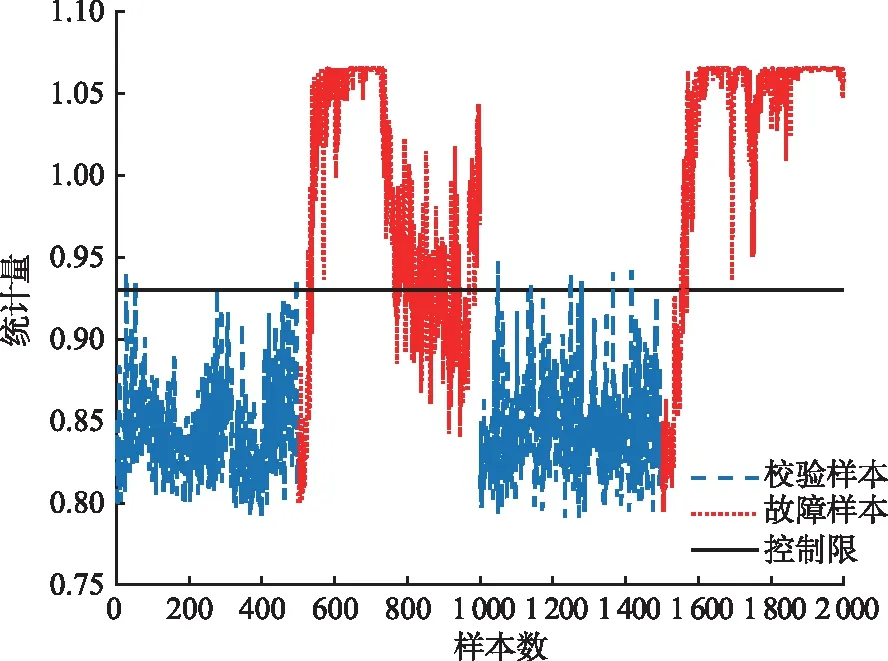
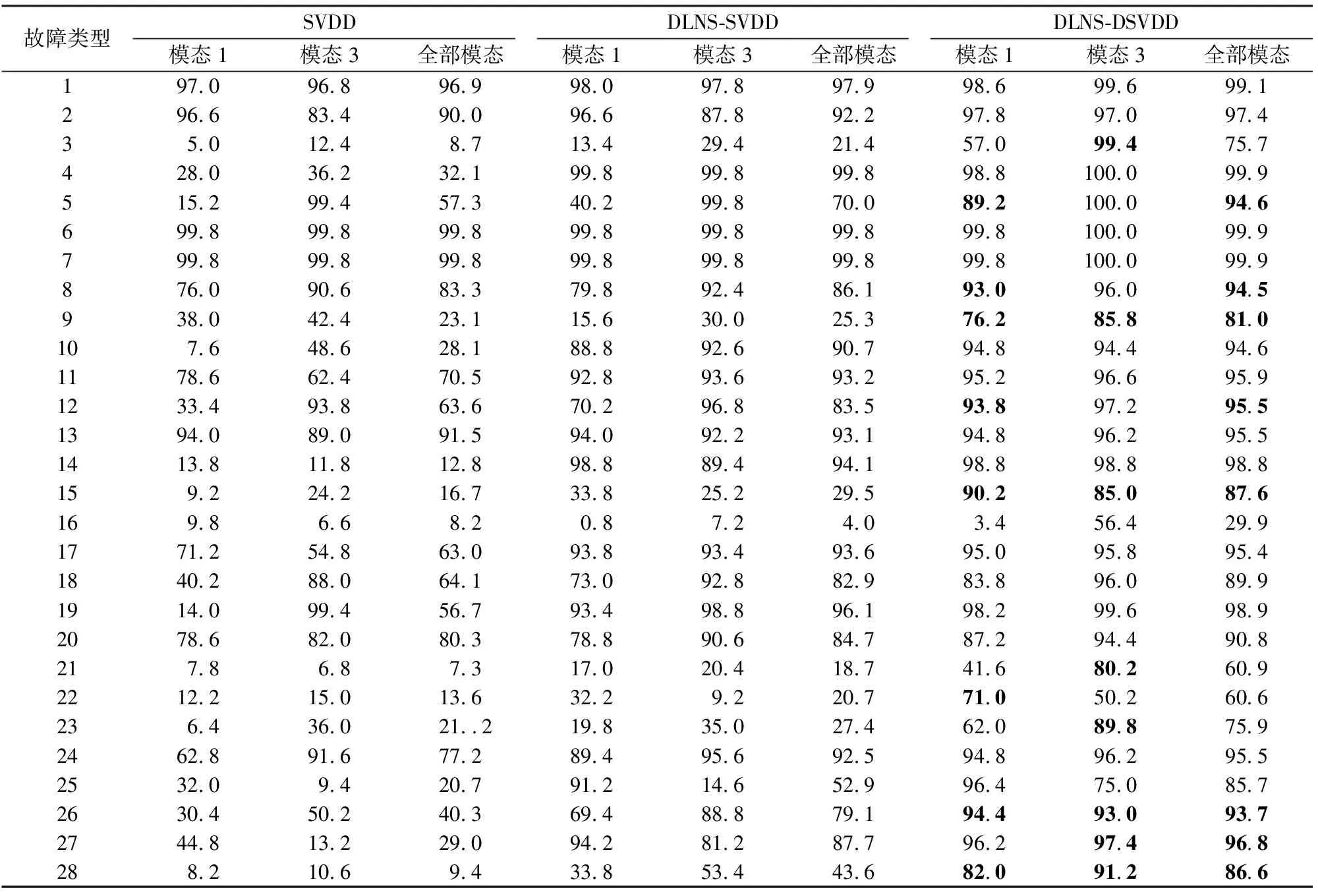
若Dz (5) (6) (7) 经过DLNS处理后,各模态数据被融合成中心相同、疏密程度相似的单模态数据,数据的多模态结构被剔除。 (8) (9) SVDD方法统计量的计算公式如式(3)和式(4)所示,可以看出SVDD方法的统计量计算是在特征空间中样本到超球体球心的欧氏距离。当过程具有多模态动态特征时,若过程在多个模态存在不同幅值的阶跃故障时,根据式(3)和式(4)无法有效地检测出故障。接下来通过修改文献[23]中一个数值例子对SVDD方法进行分析。该例子包含2个变量,由以下4个模态产生: (10) (11) (12) (13) 其中,a是过程参数,本节选取0.2;θ和t是输入变量;模态1和模态2中的e1和e2为服从N(0,0.2)的高斯白噪声,模态3和模态4中的e1和e2为服从N(0,0.8)的高斯白噪声。过程在模态1至模态4下依次正常运行4π时刻,各生成500个样本作为训练数据集。接下来过程再次在模态1至模态4下依次正常运行,但从2π时刻起在模态1和模态3的变量t上分别添加幅值为-1的阶跃信号,在模态2和模态4的变量t上分别添加幅值为-4的阶跃信号,产生共2 000个样本作为测试数据集。训练数据集和测试数据集的空间分布以及SVDD方法建立的决策边界如图1所示。从图1可以发现,决策边界未能很好地拟合正常数据,并且决策边界内存在大量的空白区域。此时决策边界内存在较多的故障样本,导致SVDD方法检测性能降低。 图1 数据集空间分布及SVDD方法建立的决策边界Fig.1 Data set spatial distribution and decision boundary established by SVDD method 基于上述分析,本文提出了基于双局部近邻标准化的动态支持向量数据描述方法,提高了SVDD方法对多模态动态过程的检测效果。本文方法分为离线建模阶段和在线检测阶段,如图2所示。 图2 故障检测流程图Fig.2 Flow chart of fault detection 图2显示了离线建模阶段和在线检测阶段的步骤。 1)离线建模阶段 ①收集不同模态的正常样本作为训练样本集X。 ④应用SVDD方法建立检测模型并使用式(3)计算控制限R。 2)在线检测阶段 DLNS-DSVDD方法在SVDD方法的基础上结合了DLNS和动态方法的优点,既可以剔除数据的多模态结构,又可以消除序列相关性对故障检测的影响。DLNS可以剔除数据的多模态结构并且扩大正常数据与故障数据之间的差异,但是无法捕获数据的动态信息;动态方法可以识别过程数据的异常变化,但是无法消除数据的多模态结构对故障检测的影响。DLNS方法和动态方法优势互补,二者结合提高了SVDD方法对多模态动态过程的检测性能。 本节通过2.2节的数值例子对本文方法的有效性进行验证,并与SVDD方法、DLNS-SVDD方法进行比较分析。3种方法的具体参数设置如下: 1)在SVDD方法中,惩罚参数C=0.5,核宽参数σ=7;2)在DLNS-SVDD方法中,近邻数k=4,双层近邻数K=5,惩罚参数C=0.5,核宽参数σ=2; 3)在DLNS-DSVDD方法中,近邻数k=4,双层近邻数K=5,滞后参数l=5,惩罚参数C=0.5,核宽参数σ=2.2。惩罚参数C和核宽参数σ可以采用交叉验证[24]方法进行确定,也可以采用经验法进行确定。本文采用交叉验证方法获取最优的惩罚参数C和核宽参数σ。 图3为SVDD方法的故障检测结果,可以发现大部分故障样本位于控制限以下,故障检测率较低。其主要原因是SVDD方法既无法识别数据的多模态特征,又无法捕获数据的动态信息。当数据具有多模态动态特征时,SVDD方法为了更好地拟合数据会将正常样本之间过多的空白区域包含在超球体中,导致了SVDD方法建立的故障检测模型泛化能力较差。若故障样本位于该空白区域中会被误报成正常样本,造成了漏报率过高,制约了SVDD方法的故障检测性能。 图3 SVDD方法故障检测结果Fig.3 SVDD method fault detection results 图4为DLNS-SVDD方法的故障检测结果,可以发现相比于SVDD方法,DLNS-SVDD方法的故障检测效果有所提升。其主要原因是DLNS-SVDD方法降低了数据的多模态结构对故障检测的影响,提高了故障检测性能。从式(7)可以看出,DLNS本质上在衡量样本与样本所在双层近邻集中心的差异,并且获得了样本相对于双层近邻集中心的变化信息[25-26]。 图4 DLNS-SVDD方法故障检测结果Fig.4 DLNS-SVDD method fault detection results 图5是经过DLNS方法处理后标准数据集的空间分布情况,通过图5可以看出标准数据集不包括过程的结构信息,原始数据的多模态结构被剔除。因此在标准数据集上应用SVDD方法进行故障检测,消除了原始数据多模态结构对故障检测的影响,检测性能得到了提高。值得注意的是,通过图5可以发现仍有部分故障样本混入正常样本之中,制约了DLNS-SVDD方法的检测性能,因此DLNS-SVDD方法的故障检测性能具有较大的提升空间。 图6为DLNS-DSVDD方法的故障检测结果,可以发现DLNS-DSVDD方法可以检测出大部分的故障样本。其主要原因是该方法既可以剔除数据的多模态结构,又可以有效识别动态过程的异常变化,大幅度提升了SVDD方法对多模态动态过程的检测性能。 图6 DLNS-DSVDD方法故障检测结果Fig.6 DLNS-DSVDD method fault detection results 图7为原始数据集单变量结构对比图,由图7可以发现,原始数据故障幅度较小,故障样本与正常样本的变化轨迹较为接近;还可以发现故障样本相比于正常样本具有明显的中心偏移现象,原始数据存在较强的动态特征。图8为标准数据集的单变量结构对比图,可以发现,故障样本与正常样本的变化轨迹发生了改变,二者之间差异被扩大化,此时数据的动态特征更易于捕获。动态方法通过量化异常条件与正常操作下过程的统计差异实现故障样本与正常样本的区分。因此原始数据在经过DLNS处理后应用动态方法可以准确地捕获数据的动态特征,SVDD方法的检测性能得到进一步提升。如图9所示,在标准数据集的基础上经过动态方法处理后,正常样本与故障样本之间存在明显界限,实现了正常样本与故障样本的分离。接下来应用SVDD方法进行故障检测,通过图9可以发现,SVDD方法的决策边界内包含大多数的正常样本,并且大多数的故障样本被排斥在决策边界之外。 图7 原始数据集单变量结构对比图Fig.7 Comparison chart of univariate structure of original data set 图8 标准数据集单变量结构对比图Fig.8 Comparison chart of univariate structure of standard data set 图9 数据集空间分布及SVDD方法建立的决策边界Fig.9 Spatial distribution of the data set and the decision boundary established by SVDD method 表1给出了3种方法的误报率(fault alarm rate,FAR)和故障检测率(fault detection rate,FDR)。通过表1可以看出,SVDD方法的故障检测率较低,仅为26.2%。其主要原因是故障样本分散在4个模态中且靠近正常样本,SVDD方法建立的决策边界为了包含尽可能多的正常样本导致了过多的故障样本混入其中,造成了SVDD方法的检测率较低。DLNS-SVDD方法的故障检测率相比于SVDD方法有所提高,达到了62.4%。其主要原因是DLNS方法可以将多模态数据融合成中心相同、密集程度近似的单模态数据,降低了数据的多模态结构对故障检测的影响,提高了SVDD方法的检测效果。但是多模态数据中部分故障尺度较小的样本经DLNS方法处理后仍混入正常样本中,导致了DLNS-SVDD方法的检测效果无法达到工业过程的检测要求。DLNS-DSVDD方法的检测率最高,达到了98.4%。其主要原因是DLNS-DSVDD方法在剔除数据的多模态结构后可以有效地捕获数据的动态特征,因此可以准确识别出故障样本。综合对比可以发现,DLNS-DSVDD方法在保证较低的误报率的情况下,具有较高的故障检测率,证明了该方法在多模态动态过程故障检测的有效性。 表1 3种方法的误报率和故障检测率 田纳西-伊斯曼(tennessee-eastman,TE)过程[27-29]作为一个完备的工业过程仿真平台,已被广泛应用于过程监控和故障检测领域。如图10所示,该过程主要包括5个转换单元、4 种反应物、2种产物、1种惰性气体和1种副产物。TE过程可以模拟正常生产过程,并且可以通过操控已知的干扰因素产生28 种不同故障的过程,部分已知故障类型如表2所示。一旦过程出现故障,该过程的所有变量都会受到影响,其中某些变量值会发生改变。 图10 TE过程基本结构Fig.10 Basic structure of TE process 表2 故障描述及变化类型 TE仿真器[30]可以模拟6种工作环境,本节选用模态1和模态3两种工况数据进行监控。TE过程生成的数据集共包含53个变量,由于生成的数据中有3个控制变量在整个过程中恒定不变,选择舍去,故本节保留其中的50个变量进行故障检测。设采样周期为0.01 h,过程在模态1下正常运行10 h后转换到模态3继续运行10 h,共采集2 000个正常数据组成训练数据集。再次让过程在模态1下正常运行5 h后引入故障,10 h后转换到模态3正常运行,15 h后引入故障,20 h后结束采集,组成测试数据集。 本节使用DLNS-DSVDD方法进行故障检测,并与SVDD方法、DLNS-SVDD方法进行比较。其中SVDD方法的惩罚参数C选取0.5,核宽参数σ选取15;DLNS-SVDD方法的惩罚参数C选取0.5,核宽参数σ选取7,近邻数k选取4,双层近邻数K选取5;DLNS-DSVDD方法的惩罚参数C选取0.5,核宽参数σ选取5,近邻数k选取4,双层近邻数K选取5,滞后参数l选取3。 图11—13分别为3种方法对于故障26的故障检测结果。通过图11可以看出,当SVDD方法处理具有多模态特征或者动态特征的过程数据时,建立的决策边界无法很好拟合正常样本,造成了过多故障样本位于决策边界内,导致了检测率较低;通过图12可以看出,DLNS-SVDD方法降低了过程的多模态特征对故障检测的影响,检测效果有所提升,但是无法捕获过程的动态信息,检测性能受到了制约;通过图13可以看出,DLNS-DSVDD方法既可以剔除数据的多模态结构,又可以消除样本间序列相关性对故障检测的影响,因此可以准确地识别故障样本,具有较高的检测性能。 图11 SVDD故障检测结果Fig.11 SVDD fault detection results 图12 DLNS-SVDD方法故障检测结果Fig.12 DLNS-SVDD method fault detection results 图13 DLNS-DSVDD方法故障检测结果Fig.13 DLNS-DSVDD method fault detection results 表3列出了SVDD方法、DLNS-SVDD方法和DLNS-DSVDD方法对模态1、模态3和全部模态的TE过程的故障检测率。通过表3可以发现,对模态1和模态3中故障类型为9,15,26,28的TE过程进行检测时,相比于SVDD方法和DLNS-SVDD方法,DLNS-DSVDD方法的检测性能均具有明显的优势。除了上述故障类型的TE过程,对模态1中故障类型为5,8,12,22的TE过程进行检测时,DLNS-DSVDD方法的检测性能相比于SVDD方法和DLNS-SVDD方法具有显著得提升,对模态3中故障类型为3,21,23,27的TE过程进行检测时,DLNS-DSVDD方法的检测性能相比于SVDD方法和DLNS-SVDD方法同样具有显著得提升。对其他故障类型的TE过程进行检测时,DLNS-DSVDD方法的检测性能在不同程度上均高于SVDD方法和DLNS-SVDD方法的检测性能。综合对比上述方法对TE过程的故障检测效果可以发现,DLNS-DSVDD方法的故障检测效果最优,检测结果证明了本文所提方法在多模态动态过程故障检测的优异性。 表3 3种方法的故障检测率 针对多模态动态工业过程数据的故障检测问题,提出了DLNS-DSVDD故障检测方法。首先,DLNS方法利用样本的局部空间信息消除了数据的多模态特征,并且扩大了正常样本和故障样本之间的差异;其次,动态方法通过量化正常样本与故障样本的统计差异,有效地捕获了数据的动态特征;最后,应用SVDD方法建立基于空间距离的统计量,准确地检测到故障样本。DLNS方法和动态方法优势互补,二者结合提高了SVDD方法对多模态动态的过程检测性能。 将DLNS-DSVDD方法应用于田纳西-伊斯曼过程进行仿真测试,并与传统方法对比分析。仿真结果表明,SVDD方法的平均故障检测率为49.7%,DLNS-SVDD方法的平均故障检测率为70.0%,而DLSN-DSVDD方法的平均故障检测率为88.2%。在平均误报率均小于5%的前提下,DLNS-DSVDD方法的故障检测率较高,因此可证明该方法的优越性。依次分析TE过程的28种故障类型,DLNS-DSVDD方法对于每种故障类型的故障检测率相比于其他2种方法均有不同程度的提高,并且除了故障类型3,16,21,22,23难以检测外,其他故障类型的故障检测率均满足化工过程的检测要求,因此可进一步证明本文所提出方法的优越性。 本文主要研究了DLNS-DSVDD方法在多模态动态过程中的实现与应用,并取得了一定的成果。但是由于实际化工过程的复杂性,早期的微小故障往往存在难以捕获的动态特征,制约了本文所提算法的检测性能。因此,未来将致力于改进DLNS-DSVDD方法,拓宽本文所提方法的适用领域。1.2 双局部近邻标准化
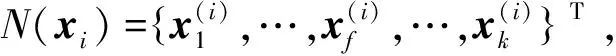

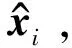
2 基于双局部近邻标准化的动态支持向量数据描述的故障检测方法
2.1 动态方法
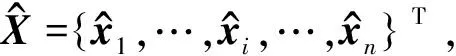
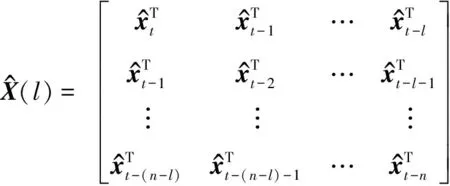
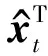
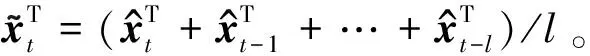

2.2 举例与检测流程
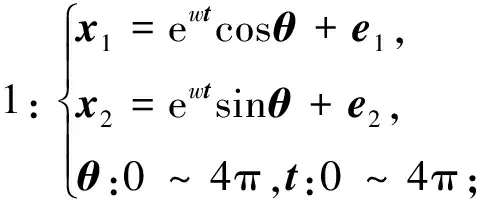
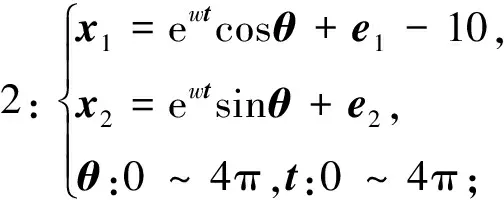

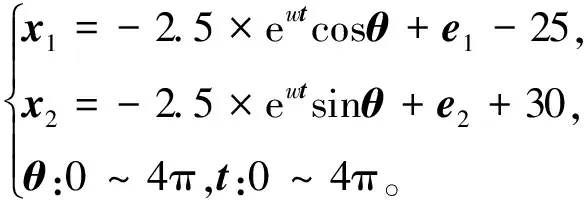
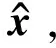
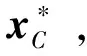

3 仿真实验
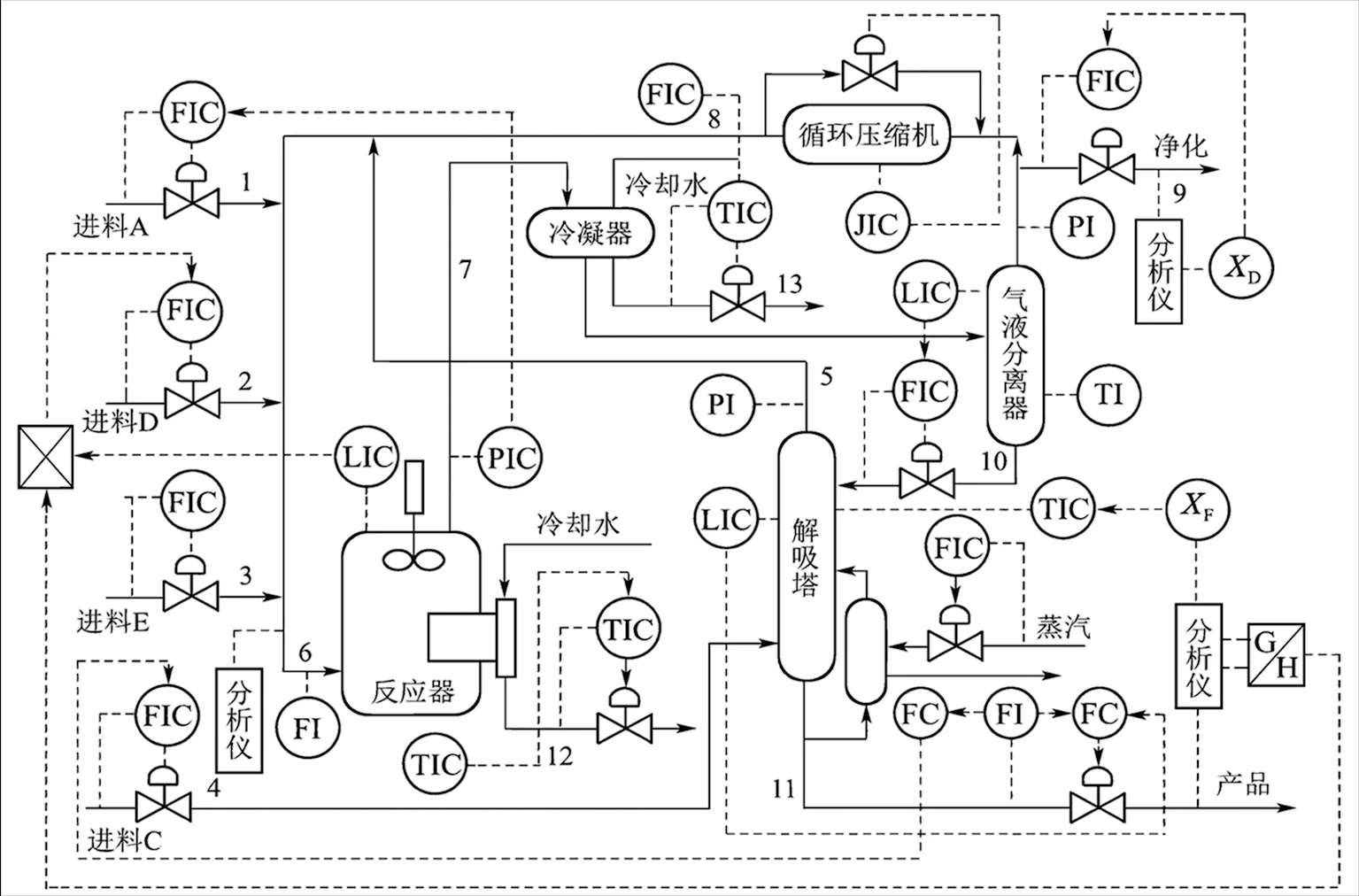
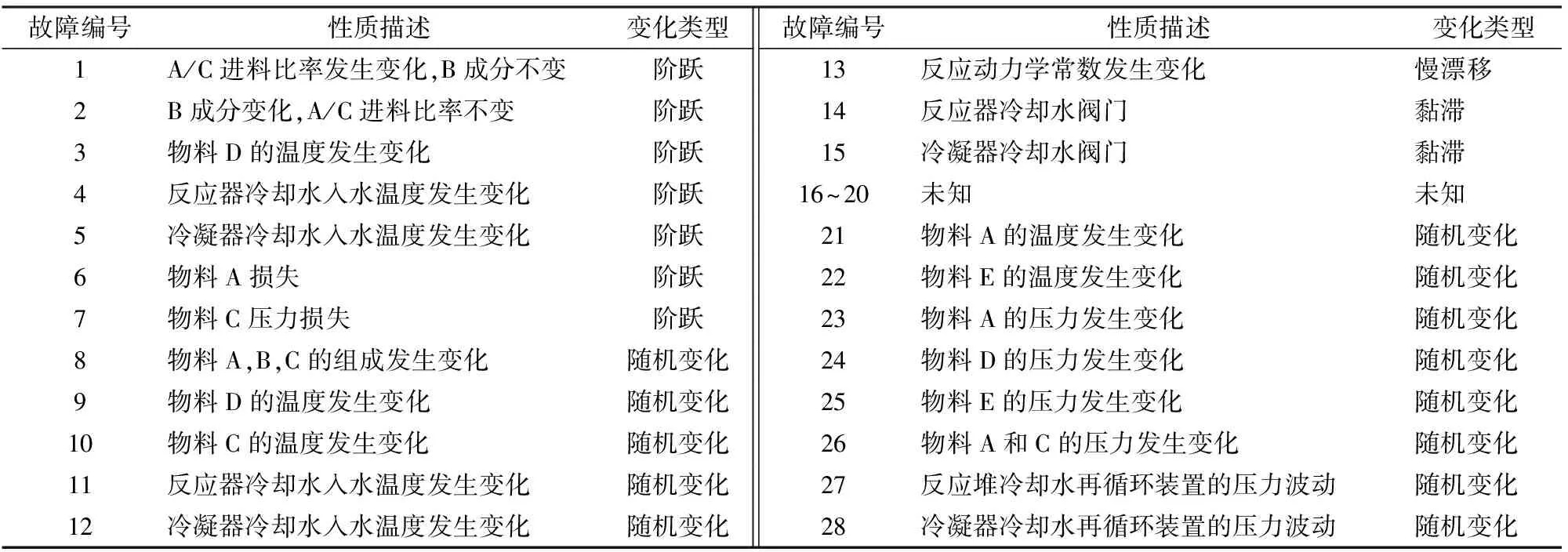
4 TE过程


5 结 语

