考虑配电网静态电压稳定性的微电网优化配置

徐艳春,张进，汪平，MI Lu

(1.梯级水电站运行与控制湖北省重点实验室(三峡大学)，湖北省宜昌市 443002；2.德州农工大学电气与计算机工程系，美国德克萨斯州卡城 77840)

0 引 言

随着国民经济的发展和人们对能源节约意识的提高，分布式电源(distributed generation，DG)因其投资小、清洁环保和发电方式灵活而被广泛应用。与常规发电机相比，风机、光伏出力具有随机性和波动性的特点，对配电网静态电压稳定性和运行经济性产生明显的影响，同时这种风险会随着DG并网容量的不断增加而放大[1-2]。特别地，风机出力曲线具有明显的反调峰特性，与配电网用电负荷匹配度较低，而光伏出力对午高峰能起到较好的支撑作用，两者具有互补的特点[3]。储能装置具有快速响应的优势，能够优化电源结构，起到削峰填谷的作用，降低系统调峰压力[4]。将一定比例的可再生能源和储能装置以微电网形式接入到配电网的合适位置，可以降低可再生能源出力波动，从而提高电网的电能质量，改善系统电压分布，减小网络损耗，降低对一次能源的需求消耗[5]。配电网内的风光储微电网配置属于高维度问题，求解计算量大。因此，选取合适的处理方法对风光储微电网进行合理配置具有重要意义。

目前，国内外学者对配电网中DG的规划问题已进行了深入的分析和研究，并取得了一定的进展。现有文献大多以威布尔分布和贝塔分布模拟可再生能源出力数据为依据，仅在满足配电网运行的不等式约束条件下进行寻优以实现可再生能源的最大接入容量，但没有结合储能装置削峰填谷的作用发挥可再生能源在时序上出力互补的优势。文献[6]在分布式电源的配置方案中重点考虑配电网运行的经济问题，通过电压偏移不等式约束实现配电网可靠运行，但分布式电源会因为其峰值出力造成的电压越限而被限制接入容量，仅适用于可再生能源渗透率较低的情况。文献[7]提出一种电压稳定指标，从电压稳定的角度分析DG的最佳接入位置，为DG的优化配置提供了指导。文献[8]将电压稳定性指标作为优化配置目标之一，通过固定权重法对各个优化目标赋予不同权重，将多目标优化问题转化为单目标优化问题实现对分布式电源的优化配置，但固定权重法中对不同目标的权重选取具有较强的主观性，不能真实反映各个目标之间的重要关系，得到的配置方案缺乏灵活性，不能方便地推广使用。文献[9]对全年按照季节进行场景划分，根据季节天数计算不同场景权重，最终得到的配置方案在考虑可再生能源全年出力特征的同时降低了计算规模。文献[10]分析了分布式发电市场环境下，配电网通过分布式光储协同规划实现各利益主体均衡。文献[11]指出风机与光伏出力时序上存在互补的特点，通过合理配置两者安装比例可以降低可再生能源出力的波动，为可再生能源的高渗透率并网提供了思路。文献[12]在含DG的配电网中以提高储能装置对DG平抑效果和减少储能系统成本支出为目标，研究储能装置的容量配置及选址情况，但在DG并网容量和位置确定的情况下，储能装置的优化配置只能降低弃风弃光，而无法从根本上提高可再生能源的渗透率。

针对以上问题，本文提出一种考虑配电网静态电压稳定性的风光储微电网系统定容选址方法。提出一种改进的综合电压稳定指标(composite voltage stability index,CVSI)作为评价微电网系统定容选址方案的指标，可以更快地计算当前配电网静态电压稳定性。同时，为解决多场景模型精确度与计算复杂度之间的矛盾，根据不同地形地区风速、光照等气象环境条件计算风机光伏全年实际出力的时序序列并进行场景缩减，得到该地区具有代表性的场景数据及对应权重；然后，根据不同场景内风机光伏出力特点来确定风光储三者的最佳容量配置比例；最后，建立以配电网静态电压稳定性和配电网运行经济成本为目标的多目标规划模型，采用改进后的多目标平衡优化器(multi-objective equilibrium optimizer，MOEO)算法对模型求解，从而实现多目标总体最优解决策。

1 考虑电压稳定性与越限的综合电压稳定指标

1.1 配电网静态电压稳定指标

配电网静态电压稳定性与有功功率和无功功率之间有复杂的耦合关系。PV曲线反映节点有功功率变化与电压之间的关系，虽然没有显式表达电压与无功功率之间的关系，但是PV曲线一般通过连续潮流法获得，已经考虑到配电网中无功功率对电压的影响。文献[13]指出，PV曲线鞍结分叉点状态对应潮流方程雅可比矩阵出现零特征值，因此PV曲线的鞍结分岔点是系统静态电压临界稳定点。

图1为电力系统PV曲线示意图，反映了电力系统中负荷消耗功率P与该负荷处电压V之间的变化关系。

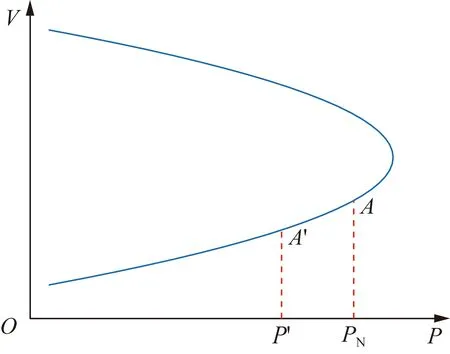
图1 PV曲线Fig.1 P-V curve

对于恒功率负载，当系统正常运行处于PV曲线下半部分A点时，系统应向负荷提供额定功率PN。如果负荷侧电压受到扰动降低，系统向负荷提供功率过低数值为P′，系统供应有功功率不足导致负荷侧电压进一步降低到达A′位置，形成恶性循环，加剧了功率不平衡。

根据戴维南等效电路可知，当线路处于最大负载时即PV曲线的鞍结分岔点时，负载侧电压与戴维南等效阻抗上的电压相等，从而可以快速求解鞍结分岔点，避免了连续潮流法中潮流方程出现不收敛、计算复杂且速度慢的缺点。文献[14]提出使用迭代算法确定距离矩阵，其中矩阵中的第m列表示母线m与控制该条母线电压的发电机之间所有路径。通过距离母线m最近的PV型发电机端口电压与负荷侧电压来计算戴维南等效阻抗上的电压ΔVm。

电力系统的运行状况时刻发生变化，当配电网的拓扑结构发生变化时就需要重新对每条母线计算迭代矩阵，计算成本较高。因此引入相对电气距离，列出发电机母线与负载母线之间的电压电流关系，如公式(1)所示。

(1)

式中：VL为负荷母线电压矩阵；IG为发电机并网母线电流矩阵；IL为负荷母线电流矩阵；VG为发电机并网母线电压矩阵；FLG和KGL表示发电机与负载母线之间的电气关系，可以通过节点导纳矩阵求出；ZLL和YGG为阻抗矩阵和导纳矩阵中对应位置的子矩阵。利用矩阵FLG可以计算得到相对电气距离矩阵RLG[15]，如公式(2)所示。

RLG=A-abs[FLG]=A-abs[|YLL|-1|YLG|]

(2)

式中：A为与RLG维度相同的全1矩阵；abs表示对矩阵内元素取绝对值；YLL和YLG为导纳矩阵中对应位置的子矩阵。

RLG中的元素表示负载与系统中所有发电机的相对电气距离，与通过迭代矩阵确定最短路径方法相比计算量大幅降低。

比较矩阵RLG每列的元素大小，可以确定距离指定母线最近的发电机，从而计算戴维南等效阻抗压降ΔVm，如公式(3)所示。

(3)

不同的电压稳定指标由于采取不同的近似处理，都会存在一定程度上的误差。电力系统中某条母线在电压临界稳定状态时，相邻母线电压也会产生大幅度电压波动现象，因此加入修正因子β，如公式(4)所示。

β=1-(max|Vmax-Vmin|)2

(4)

式中：Vmax为系统中最高母线电压标幺值；Vmin为系统中最低母线电压标幺值。简化电压稳定指标(simplified voltage stability index,SVSI)计算公式如公式(5)所示。

(5)

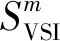
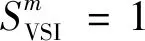
当发电机中过励磁限流器和定子限流器工作时，发电机会失去电压控制进入PQ工作模式，发出定额的有功功率与无功功率。因此计算各母线SVSI指标时需要改写节点导纳矩阵，重新确认距离该母线最近的PV型发电机。

1.2 SVSI对含新能源配电网的适应性分析

传统配电网一般呈放射状，功率沿馈线方向传输，电压逐渐降低，线路末端电压会因有功、无功负荷变化造成大幅度的电压波动。在现代配电网中，光伏、风机等新能源的接入可以提高配网电压稳定性，但由于DG并网位置和实时出力易受地理位置和环境影响，如果不能与当地负荷协调运行，不仅不会对维持电网电压起到积极性作用，还会加剧配网电压波动，导致母线电压低于电能质量国家标准(GB 12326—2000)中提出的对电压波动的限制。实际运行工作中，电压波动超过允许范围会对配网电力设备和用户生产设备造成危害，必须采取切机切负荷、改变网络拓扑结构等安全保护措施。

与其他电压稳定性指标相比，SVSI具有灵敏度高，变化平滑稳定不易跃变的优点[16]，但该指标认为配网电压稳定性受PV节点发电机影响。目前大量分布式电源以PQ型微电网形式并网接入，其出力的不确定性使该指标对配网适应性较差，无法反映配网电压越限问题。电压质量评估指标作为系统调度的参考依据，为保证系统正常运行，应该同时反映常见的电压越界问题。

1.3 改进后的静态电压稳定指标

鉴于配电网特别是DG并网后容易出现的电压越限问题，本文构造一个功能性函数，在节点电压处于安全允许范围内时该函数值很小，接近于0，当即将发生电压越限时，函数值迅速增大起到安全预警的作用。将该函数与SVSI相结合，构造出综合考虑电压稳定性与越限的质量指标。

模拟阶跃特性的函数f(x)可以满足对电压偏移越限预警的需求，f(x)计算方法如公式(6)所示。

(6)

式中：x为监测状态变量；α、c为待定常数，可以用来调节函数的阶跃特性。该函数阶跃特性如图2所示。

图2 函数f(x)特性Fig.2 Function characteristics of f(x)

1)当x∈[-α，α]时，f(x)≈0；

2)当x∈[-∞，-α)∪(α，+∞]时，f(x)在x≈±α处快速上升，迅速达到稳定值1。

将电压偏移作为x输入，对函数进行改造后可得到反映节点电压越限的函数，如公式(7)所示。

(7)

式中：UN为母线m额定电压；a的取值取决于配电网供电质量规范规定的电压允许偏差值；b和c决定函数阶跃增幅斜率。因为f(Vm)的数值对b的取值极为敏感，在不同电压等级配电网中b的取值不变。当电压偏移超过允许范围时，指标数值应超过1，以此为根据设置c的数值。根据不同配电网对电压偏移的不同要求，a、b和c的具体取值参考文献[17]，如附录表A1所示。

综合公式(5)和公式(7)可以得到考虑电网母线电压稳定性与越限的综合电压质量评估指标(composite voltage stability index，CVSI)，如公式(8)所示。

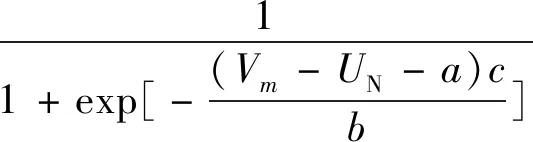
(8)

2 风光储系统多场景缩减模型

可再生能源出力的波动性限制了其在电网中的大规模接入。为提高电网中可再生能源渗透率，将含风光储的微电网系统作为整体接入配电网中，利用风光互补的特点降低可再生能源出力波动，根据风机和光伏出力数据和储能装置配置成本，计算风光储三者最佳配置比例，最后通过多场景缩减技术对全年场景进行缩减，从而降低优化配置的计算量。

2.1 考虑风光出力互补的多场景分析

风机与光伏的出力受到所处地理环境和气候的影响，根据不同地形的气象数据和DG出力方程计算得到风机和光伏全年8 760 h的时序出力数据。在不考虑加入储能装置情况下，通过公式(9)计算不同地区光伏安装容量的各自最佳安装比例η，降低总可再生能源的日出力波动，减少系统的调峰压力。

(9)

为提高分布式电源配置方案效果，应该选取尽可能多的原始数据点。如果无法获取全年数据，应尽量保证四个季度中数据所占比例相同，避免某个季节所占权重过大而影响最终配置方案。

在选址规划过程中，如果直接将全年DG出力数据运用到优化过程中会导致维度剧增。考虑到K-means方法易受初始点选取不准确影响聚类效果的缺点，本文采用基于K-means++的多场景分析法对不同地形的全年数据进行聚类，从而得到多个具有代表性的场景数据及其对应概率。与仅考虑四季出力特点的同类方法相比，其保留场景数目更多，能够更好地反映可再生能源出力的波动特点，虽然K-means++会丢失部分极端场景，但极端场景内可再生能源预测误差较大，数据可信度较低，对最终配置方案影响较大，降低可再生能源的渗透率。对于出现概率极低的极端场景，可以在配电网实际运行中通过发电机自动发电控制或日前调度等更小时间尺度上进行处理。本文在优化计算中对场景进行加权求和考虑到了绝大多数场景，一定程度上降低了电网运行中因调度而产生的弃风弃光现象，具体步骤如下：

1)根据风光最佳配置比例得到描述三种不同地形可再生能源全年出力数据的365×72维矩阵，用ξs表示不同场景。

4)将距离最远的场景添加为新的场景质心，重复进行步骤3)直至场景质心数到K。

聚类个数K的取值决定计算的复杂度和缩减后场景包含特征的多样性。随着聚类个数K的增加，每个组内的聚合程度逐渐提高，聚类集合内部距离和逐渐变小，而当K超过最佳聚类数后距离减小的速度会减慢。考虑到可再生能源特征多样性较强，本文采用中肘方法[18]确定聚类个数K。误差平方和(sum of squared error，SSE)的计算如公式(10)所示。

(10)

式中：K为聚类数；Ck为聚类结果中第k簇；p为该簇内样本点；mk为Ck的质心；SSE为所有样本的聚类误差，代表了聚类效果的好坏。随着聚类个数K的增加，样本的划分会更加精细，每一簇内的聚合程度会逐渐提高，平方误差和逐渐变小。当聚类个数超过最佳聚类数后，平方误差和的下降速度会减慢形成肘部特征，从而得到最佳聚类数K。

2.2 储能装置容量计算

储能装置能量双向流动的特点为高比例可再生能源的接入提供了可能。文献[19]指出微电网内储能装置的投资成本由储能装置容量、储能功率和逆变器安装成本三部分组成，如公式(11)所示。

Cess=ηBBess+ηPPess+ηinvPess

(11)

式中：Cess为储能装置投资成本；ηB为储能容量成本系数；Bess为储能装置容量；ηP为储能功率成本系数；Pess为储能装置输出功率；ηinv为逆变器成本系数。

储能装置容量与额定功率之间成正比[20]，如公式(12)所示。

Bess=χ×Pess

(12)

式中：χ为储能装置能量倍率。

本文从储能系统对DG出力的平抑效果和减少储能系统投资成本支出两个方面，研究储能装置容量与风机光伏两种DG的配比方案，确定储能装置安装容量。在可再生能源出力场景聚类结果中，用第k簇的质心数据表示第k个典型日中可再生能源出力数据。第k个典型日内储能装置容量配置的目标函数如公式(13)所示。

(13)

储能装置充放电功率以及储能装置容量的求解过程中，应考虑到储能装置充放电效率影响，以及限制储能装置荷电状态以提高储能装置使用寿命[5]，如公式(14)和公式(15)所示。

(14)

(15)

式中：Pmax为储能装置充放电功率极限；Pess(t)为t时刻储能装置充放电功率；SOC(t)为t时刻储能装置荷电状态;σ为储能装置自放电比例；ηc和ηd为储能装置的充电效率和放电效率；ΔT为最小调度时间尺度。

储能装置容量的确定应考虑全年各个典型日的可再生能源的出力特点，是不同典型日下储能装置最佳容量加权求和。储能装置容量Bess计算方法如公式(16)所示。

(16)

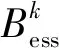
3 多目标平衡优化器算法

DG规划问题中需要确定DG并网容量和位置，属于多维度、非线性、变量变化范围大的多目标优化问题。虽然通过多场景缩减等手段降低了计算量，但对智能优化算法性能要求仍然较高。由文献[21]可知，与其他优化算法相比，平衡优化器 (equilibrium optimizer,EO) 算法在单目标测试函数中优势明显，具有更强的全局搜索和局部探索能力。本文对EO算法进行改进，从而得到一种改进后的多目标平衡优化器算法，并进行相关测试。

3.1 平衡优化器算法

EO算法是受到物理学中溶液质量平衡方程的启发而提出的一种新型智能算法。溶液质量变化量由流入溶液质量、流出溶液质量和溶液内新产生质量三部分组成，可以用一阶微分方程式(17)表示。

(17)

式中：V为控制容积；C为控制容积内的溶液浓度；Q为流进或流出控制容积的容量流速；Ceq为控制容积内部平衡状态时的浓度；G为控制容积内部的质量生成速率。

整理可得EO算法中浓度更新公式为：

(18)

式中：C0为溶液初始浓度；λ为浓度流转率；指数项系数F=exp[-λ(t-t0)]。

在公式(18)中，第一项溶液平衡状态浓度Ceq表示在适应度较好个体基础上进行位置更新；第二项(C0-Ceq)F表示当前个体与平衡池内适应度较好个体之间的差值决定算法的全局搜索能力；第三项G(1-F)/(λV)决定算法的局部开发能力，受G的取值影响较大。

在EO算法迭代过程中，F和G的取值决定优化过程中算法的全局搜索能力和局部开发能力。随着迭代过程的进行，算法应该逐渐侧重于局部开发能力减弱全局搜索能力，同时在最优解附近应减少波动范围提高算法精确度，因此将变量t和G定义为指数型衰减变量，如公式(19)—(22)所示。

(19)

G=G0exp[-λ(t-t0)]=G0F

(20)

G0=GCP(Ceq-λC)

(21)

(22)

为减少算法需要设置参数的个数，提高运行速度，将t0定义为：

(23)

式中：a1为全局探索权重系数；r为[0,1]之间随机数；sign为符号函数。

整理后可得：

F=a1sign(r-0.5)[exp(-λt)-1]

(24)

3.2 平衡优化器算法的改进

种群在初始化过程中，个体多样性对后期迭代过程中寻优效果影响较大。微电网优化配置中微网容量波动范围较大，对初始序列的要求更高。常规方法采用随机序列进行初始化，随机性较强，不具有遍历性，容易陷入局部最优，而混沌变量具有随机性、遍历性和规律性的特点[22]。不同的混沌映射算子对混沌寻优过程有很大的影响，Tent映射比Logistic映射具有更好的遍历均匀性和更快的迭代速度，因此本文通过Tent映射生成混沌序列对个体进行初始化，如公式(25)所示。

(25)

式中：μ为混沌参数；yi为混沌变量序列；i为变量序号。

得到混沌变量序列yi后，对其做逆映射到相应的个体搜索空间得到变量序列xi。

(26)

在单目标优化算法中，适应度是个体是否被保留的唯一参考指标。在多目标优化算法中，不同目标函数的适应度无法直接进行优劣判断，选择保留个体的步骤如下：

1)计算全部个体的所有适应度值，根据不同目标函数适应度的支配关系筛选出非支配个体并进行存档。

2)对求解空间进行等面积网格划分，计算每个网格内非支配个体的数量并进行拥挤度排序。

3)为保证最终结果中帕累托前沿的覆盖性，采用轮盘赌思想优先保留拥挤度比较低的个体，如公式(27)所示。

(27)

式中：P(xi)为xi被保留存档概率；crowd(xi)为xi拥挤程度；N为Pareto解的数量。

4)当存档个体数量超过上限时，对存档个体按照支配关系和拥挤程度进行淘汰。

3.3 测试函数验证

在UF1—UF6测试函数[23]对MOEO算法进行测试，通过多目标优化算法评价指标与采用随机序列初始化的多目标平衡优化器(random multi-objective equilibrium optimizer,RMEO)算法以及目前被广泛应用的多目标灰狼优化(multi-objective gray wolf optimizer,MOGWO)算法、多目标粒子群优化(multi-objective particle swarm optimization,MOPSO)算法、多目标蚁狮优化(multi-objective ant lion optimizer，MOALO)算法、多目标差分算法(multi-objective differential algorithm，MODA)、多目标多节优化算法(multi-objective multi-verse optimization,MOMVO)以及强度帕累托进化算法(strength pareto evolutionary algorithm 2,SPEA2)进行对比。

世代距离(generation distance,GD)指标表示算法获得的非支配解集与真实解集的平均最小距离，GD值越小表示算法收敛性能越好[24]。反世代距离(inverted generational distance,IGD)评价指标用来评价算法的收敛性能和分布性能，IGD值越小表示算法的综合性能越好[25]。超体积(hypervolume,HV)指标表示算法获得的非支配解集与参照点围成的目标空间中区域的体积，用来评价算法的收敛性能和分布性能，HV值越大表示算法的综合性能越好。间距(spacing,SP)指标表示算法获得的非支配解集中每个解到其他解的最小距离的标准差，SP值越小表示非支配解集分布越均匀。

在测试函数仿真中，改变MOEO算法参数设置发现当a1=2.5、a2=1、GP=0.5时，算法的全局搜索能力和局部探索能力达到均衡，所得到的最优解集稳定性较好。将各个算法中最大迭代次数、种群规模、Pareto解集存档数量均设置为100。每种算法进行5次优化后4种评价指标的平均值和标准差见附录表A2—A7。从表中数据可以看出，与随机初始个体的RMEO算法相比，MOEO仅在测试函数UF1中IGD-AVG和SP-AVG表现不佳，在其他5种测试函数中均表现出明显优势。

与其他6种多目标优化算法相比，MOEO算法在测试函数UF1、UF3和UF5中4种指标的平均值和标准差均为最佳；在测试函数UF4和UF6中分别只有SP-AVG和HV-STD一项指标不是最佳，但与MOGWO、MOPSO和MOALO等算法相比仍具有优势；在测试函数UF2中，HV-STD、IGD-STD和SP-AVG虽然不是7种算法中的最佳数据，但与最佳数据差别极小，排名为第二或者第三。综上所述，没有一种算法在6种测试函数中所有评价指标中均排名第一。MOEO算法在一定程度上保留了EO算法在单目标优化算法上的优势，与其他多目标优化算法相比通过MOEO算法得到的Pareto解集在收敛性和分布性上优势明显。

在得到Pareto解集后，本文应用模糊集理论[26]确定Pareto最优折中解。根据模糊集理论，可以通过公式(28)计算所有Pareto解的适应度。

(28)

式中：ffit(xi,O)为xi在目标函数O中的适应度；f(xi,O)为xi在目标函数O中的函数值；FO,min为所有个体中目标函数O中最小值；FO,max为所有个体中目标函数O中最大值。

各个Pareto解的综合适应度可以表示为：

(29)

式中：ffit(xi)为xi的综合适应度；R为目标函数数量。

综合公式(28)和公式(29)，即可选取综合适应度最高的Pareto解为Pareto最优折中解。

3.4 微电网优化配置流程

微电网优化配置流程如图3所示。首先根据风光出力特点和储能装置经济成本计算不同地区风光储容量的最佳配置比例；其次初始粒子设置中用不同维度分别表示微电网并网节点和微网内风光储并网容量，将CVSI数值和经济成本作为两个目标函数；再次通过改进后的多目标平衡优化器算法获得微电网配置方案的Pareto解集；最后根据各个Pareto解的综合适应度确定Pareto最优折中解。

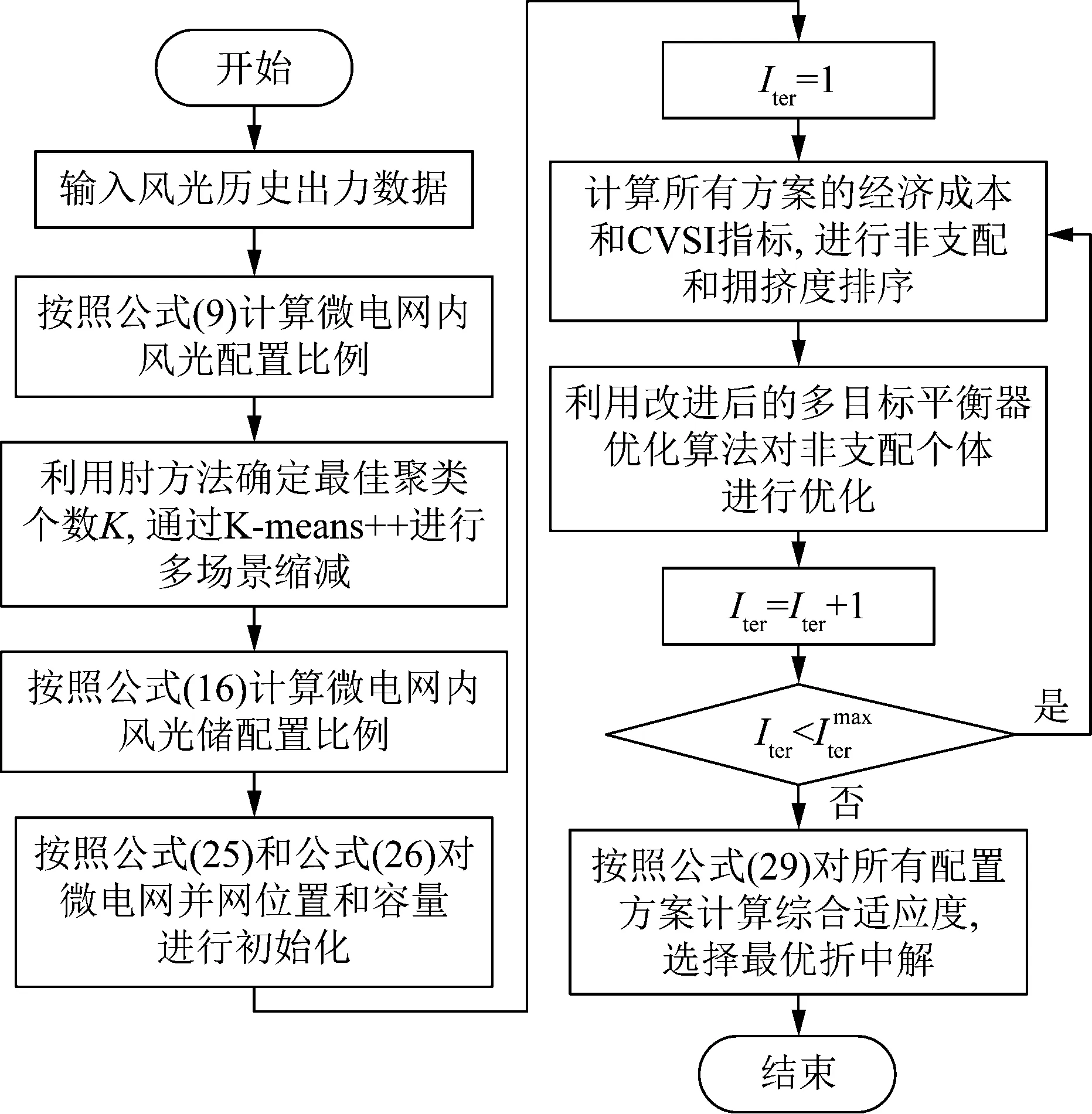
图3 微电网优化配置流程Fig.3 Flow chart of microgrid optimal configuration

4 仿真分析

4.1 综合电压稳定指标仿真验证

为验证本文提出的CVSI在含DG主动配电网中的有效性，以IEEE 33节点配电网系统作为仿真算例进行分析，系统结构见附录图B1，并与文献[27]中电力系统静态电压稳定评估指标L和文献[28]中基于支路电压方程的在线电压稳定指标D进行对比。

目前多数DG通过变频器来实现有功功率和无功功率的解耦，可以将其看作PQ节点并网。按照文献[29]，在IEEE 33节点模型中将容量为系统总负荷20%的DG均匀分配接入节点6、18、31，并进行数据仿真试验，在仿真过程中保持其余各个节点负荷按照相同速率从0开始增长，如图4所示。

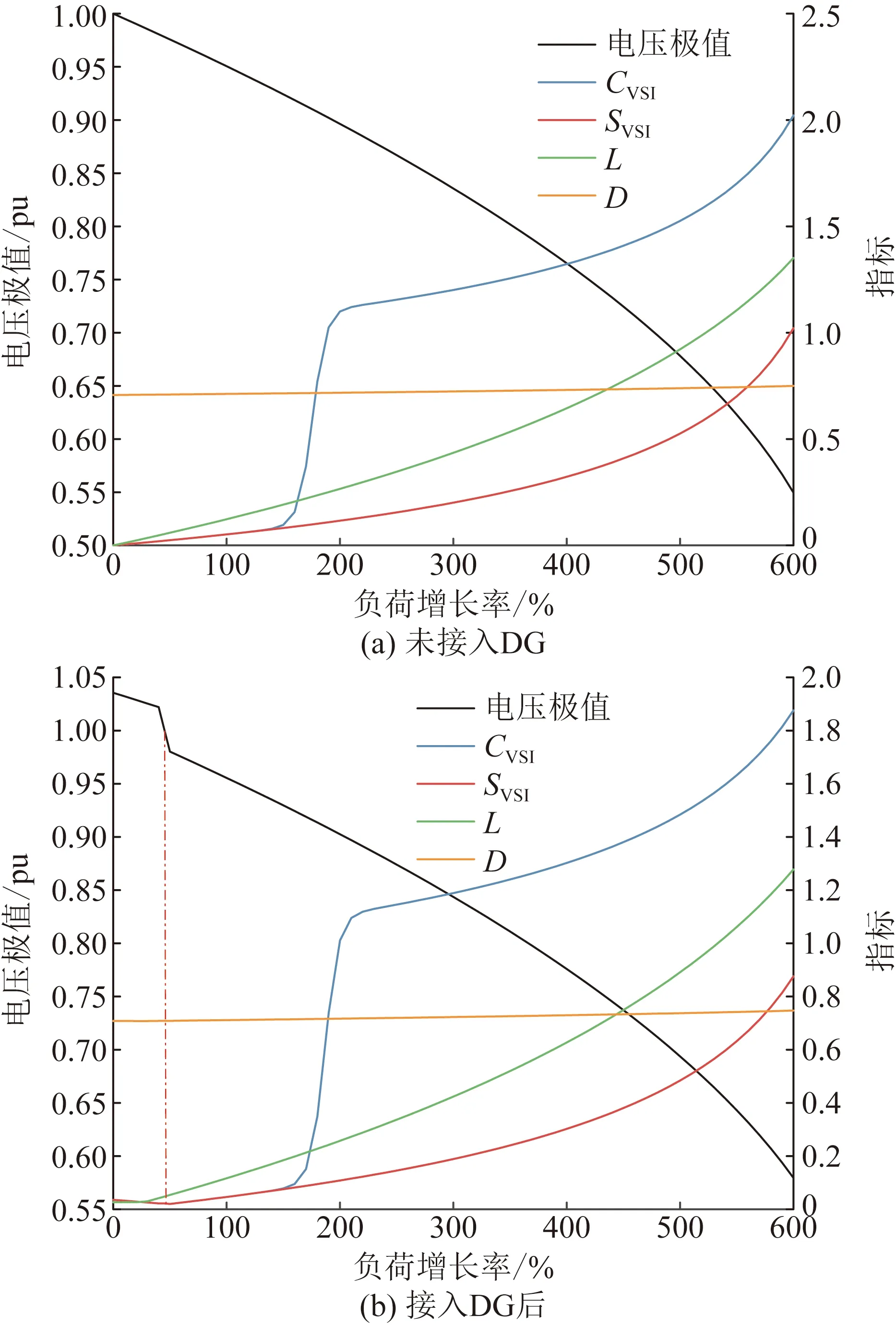
图4 IEEE 33节点系统中指标及电压极值随负荷增长变化曲线Fig.4 Indices and voltage extreme value change with load growth in IEEE 33-node system

由图4(a)可以看出，当SVSI=1时，母线最低电压为0.55 pu；当L=1时，母线最低电压为0.65 pu，均远远超出额定标准。D指标则始终未达到1，表示系统处于稳定状态。而当CVSI=1时，系统母线电压极小值为0.902 pu，系统母线电压处于安全范围内。如图4(b)所示，将DG容量按照系统总负荷功率20%接入后，高渗透率分布式电源的接入改变了电网中潮流原有方向，系统母线电压最高达1.04 pu，系统稳定性相对较差；随着负荷增加，电压稳定性先上升后下降，与其他静态电压稳定性指标相比，CVSI在电压越限时能够达到预警值，从而发挥作用。

类似地，在PG&E-69模型中将容量为系统总负荷40%的DG接入节点12、55、65、67进行数据仿真实验。不同方法的计算时间对比如表1所示。

表1 不同方法的计算时间对比Table 1 Computing time comparison of different methods

由于L指标需要多次计算选择最近的PV型发电机判断是否越限，与CVSI仅需根据相对电气距离计算最近PV型发电机状态相比，计算时间更长，且这种差距会随着配网母线和并网DG数量的增加更加明显。综上所述，所提出的CVSI不仅在配网母线电压偏移较小时，具有SVSI、L、D指标表示配网电压稳定性的功能，而且在母线电压偏移较大时可以弥补几种指标的不足，反映出配网电压越限问题。更快的指标计算速度也能够缩短微电网优化配置的运算时间。

4.2 多场景缩减模型仿真验证

根据高海拔地区、沟壑地区以及平原地区的历史气象数据和风机光伏发电性能参数指标计算全年输出功率并归算到标幺值，如附录图B2—B4所示。

通过公式(9)计算可知，平原地区风机光伏两种DG装机容量应设置为1∶0.34，高海拔地区装机容量比1∶0.15，沟壑地区装机容量比为1∶0.11。

将三种地形同一天内24 h可再生能源出力数据看作一条“1×72”时间序列，通过K-means++方法对一年内365个时间序列进行特征聚类，不同K值下簇内平方误差和如图5所示。

由图5可知，当K>22时簇内平方误差和下降速率减慢，根据肘方法可知最佳聚类数K=22，每种场景占比如图6所示。

图5 不同K值下簇内平方误差和Fig.5 Sum of square errors in clusters with different K values

图6 每种场景占比Fig.6 Specific proportion of each scenario

根据可再生能源日出力数据标准差的大小，将储能安装成本换算系数γ设置为0.01。代入公式(13)后得到平原地区风机装置容量、光伏装机容量、储能装置容量三者最佳配置比例为1∶0.34∶0.33，高海拔地区装机比例为1∶0.15∶0.65，沟壑地区装机比例为1∶0.11∶0.65。

4.3 微电网系统定容选址仿真

考虑到IEEE 33节点系统中节点数量和负荷水平微电网配置的个数设置为4。MOEO算法中a1=2.5、a2=1、GP=0.5，种群规模为20，最大迭代次数100，Pareto解集存档数量100。种群个体编码中前4列表示微电网并网位置，采用整数编码，后4列表示微电网并网容量，微电网内风光储配置比例按照4.2节中最佳比例进行配置，迭代计算中删除CVSI数值大于1即不符合配电网静态电压稳定标准的配置方案。风光储设备的投资成本设置参考文献[30]，即风机投资成本为13 800 元/kW，光伏投资成本为15 400 元/kW，储能投资成本为2 170 元/(kW·h)。沟壑地区由于山体遮挡需要额外安装光伏支架成本为2 310 元/kW，网损成本为0.7元/(kW·h)。

将通过MOEO算法得到的Pareto解集代入式(28)计算适应度后如图7所示。

图7 帕累托最优前沿Fig.7 Pareto optimal frontier

根据式(29)计算所有Pareto解的综合适应度后可知最佳配置方案是A点，即在节点9、17、31和32分别并入624.5、1 395.6、2 109.6、1 923.2 kW的风光储系统。根据三者最佳容量配置比例和设备型号容量限制，最终配置方案如表2所示。

表2 IEEE 33节点系统中MOEO算法优化结果Table 2 Optimization results of MOEO algorithm in IEEE 33-node system

此时CVSI为0.024 9，投资成本为7 842.9万元，全年网损共71 236.3 kW·h。

当不考虑电压稳定性指标，仅考虑配电网运行经济成本时，在目标函数中添加罚函数保证配电网电压偏差不大于10%，其余算法参数设置保持不变，在IEEE 33节点系统仿真结果如表3所示。

表3 不考虑电压稳定性时IEEE 33节点系统中优化结果Table 3 Optimization results in IEEE 33-node system without considering voltage stability

由于目标函数中仅考虑经济成本，与表2方案相比可再生能源接入容量下降15.2%，投资成本为4 612.7万元，全年网损为51.2 kW·h；但电压稳定性降低，CVSI为0.032 8。

在种群规模与最大迭代次数与MOEO算法相同前提下，通过MOGWO计算得到最优配置方案如表4所示。

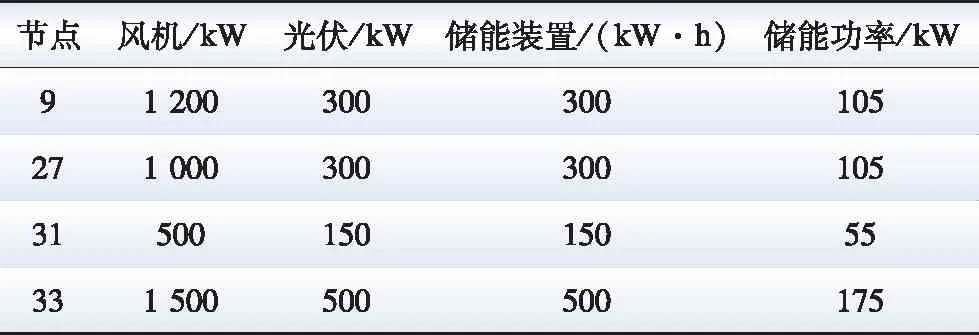
表4 IEEE 33节点系统中MOGWO算法优化结果Table 4 Optimization results of MOGWO algorithm in IEEE 33-node system

此时CVSI为0.026 7，投资成本为8 279.3万元，全年网损共78 542.4 kW·h。

对表2和表4数据进行分析可以发现，两种算法在IEEE 33并网节点的选择有一半相同，具有合理性，但MOGWO算法由于后期局部寻优能力较弱，在节点9、27和33的配置方案近似一致，陷入局部最优。两种算法所得配置方案中静态电压稳定性因为已经接近稳定极限，指标近似相同；在成本方面MOEO算法下降了5.27%。

类似地，本文在PG&E-69系统中采用MOEO算法与MOGWO算法进行优化计算。PG&E-69节点系统如附录图B5所示，由于节点数量和支路数量较多，将微电网优化配置个数设置为5。其余算法参数设置相同，最佳配置方案如表5和表6所示。

表5 PG&E-69中MOEO算法优化结果Table 5 Optimization results of MOEO algorithm in PG&E-69 system

由表5可知，此时CVSI为0.118 0，投资成本为2 852.5万元，全年网损共673.7 kW·h。

由表6可知，此时CVSI为0.127 6，投资成本为3 714.5万元，全年网损共1 070.3 kW·h。PG&E-69系统中两种配置方案对比结论与IEEE 33相同，即MOEO算法在静态电压稳定性和经济成本均表现出一定优势。

表6 PG&E-69中MOGWO算法优化结果Table 6 Optimization results of MOGWO algorithm in PG&E-69 system

表7为两种算法在IEEE 33和PG&E-69系统中得到的Pareto解集中非支配解数量。MOEO算法得到的Pareto解更多，说明所得解集覆盖性更好，可以提供更多的配置方案选择，更适合于微电网定容选址规划中。

表7 两种算法获得Pareto解的数量Table 7 The number of Pareto solutions obtained by the two algorithms

5 结 论

本文以配电网静态电压稳定性和运行经济性为目标，考虑了配电网不同地形下可再生能源出力特点，通过改进后的MOEO算法解决以风光储系统为主体的微电网定容选址问题，实现高比例可再生能源的接入。具体结论如下：

1)针对DG接入容易造成配电网节点电压越限的问题，对现有的静态电压稳定性指标进行改进并提出改进后的指标CVSI。该指标一方面能够反映配电网电压稳定性和电网越限问题，另一方面能够节约计算时间，适合于风光储微电网系统在配电网优化配置中的高维度计算。

2)风光储系统能够降低可再生能源的出力波动性，利用K-means++方法将DG全年出力场景进行缩减，根据不同场景及其对应概率来计算风光储三者最佳容量配置比例，降低了后期微电网定容选址问题中的计算量。

3)对单目标优化效果优异的EO算法进行改进，得到优化多目标问题的MOEO算法。在标准测试函数上与其他6种多目标优化算法相比，MOEO算法表现出稳定的寻优能力。通过在IEEE 33和PG&E-69进行仿真，结果表明MOEO算法在优化效果和Pareto解集覆盖性中具有优势。