基于社交网上演化博弈的光伏台区用户需求响应特性研究
范辉,罗蓬,王弘利,梁纪峰,李乾,杨军,吴赋章
(1.国网河北省电力有限公司,石家庄市 050021;2.国网河北省电力有限公司电力科学研究院,石家庄市 050021;3.武汉大学电气与自动化学院,武汉市 430072;4.国网河北省电力有限公司石家庄供电分公司,石家庄市 050000)
0 引 言
在“双碳”目标和新型电力系统建设下,分布式光伏发电由于其低碳环保、投资成本小等特点,得到迅猛发展。然而,光伏发电具有的强波动性和不确定性等限制了其大量接入电网。利用需求响应措施提高光伏就地消纳以及协调含高比例分布式光伏台区之间的运行是实现配电网经济稳定运行的主要手段。而实际中用电用户与电网分属于不同利益主体,用户对电价或激励措施响应特性复杂,导致精准的需求响应措施难以实施。因此,研究用户侧需求响应特征是新型电力系统建设过程中需要解决的一项重要课题[1-2]。
目前,国内外研究者针对这一问题进行了初步研究。在电力市场中,基于用户不同的响应方式,需求响应可以分为基于激励和基于价格的需求响应[3]。文献[4]采用弹性系数刻画用户响应量与电价或激励之间的关系,其将用户的响应量与电价简化成正比关系,该方法较为粗糙。文献[5]根据消费心理学原理将用户的需求响应度用线性分段函数进行拟合,其与真实需求响应情况仍有较大差异,无法准确描述。考虑到配电网运营商与用户为不同利益主体,也有研究者从博弈视角[6]分析用户响应特性,文献[7]根据现有的光伏上网政策,在光伏聚合商和用户之间建立了基于Stackelberg博弈的需求响应模式。文献[8]基于运营商和用户聚合代理商之间的互动模式,建立主从博弈模型并利用双层优化算法进行求解。但文献[7-8]将用户群体视为利益共同体,采用聚合器模型描述用户群体与配电网运营商之间的博弈关系,且认为用户为完全理性经济人[9],总能寻求利益最大化,忽略了用户群体为有限理性和异质性的多利益主体[10-11]。现有文献关注了用户之间的博弈特征,文献[12]基于合作博弈理论,建立了用户之间的智能用电博弈模型。文献[13]以智能住宅小区用户个体为研究对象,在用户之间建立演化博弈模型,并利用复制动态方程进行了求解。但是,上述研究中未考虑现实用户之间存在的复杂信息交互过程对用户响应的影响。
综合可知,现有关于用户需求响应的研究中主要存在三大不足:1)采用弹性系数法将用户响应量视为电价或激励的比例函数,该方法较为粗糙;2)忽略了用户群体之间的博弈关系;3)以用户个体为研究对象的演化博弈模型未能充分考虑用户社群系统中信息交互对用户响应的影响。
针对上述问题,本文首先考虑光伏用户社群系统在台区内部的信息传递结构,通过社交网络这一复杂网络建立台区光伏用户之间的信息交互模型;其次,计及用户信息交互影响以及实际用户的有限理性特征,将电价或激励措施视为外部影响条件,基于社交网络上的演化博弈模型建立台区光伏用户需求响应决策模型,并设计相应求解算法;最后,通过仿真算例分析不同用户社交网以及电价或激励措施对用户需求响应特性的影响,利用所提方法与实际运行数据对比验证所提模型的合理性和有效性。
1 用户社交网络模型
光伏台区用户之间的社交关系和信息交互将影响用户对电价激励的响应程度,反映用户之间的社交关系和信息交互的网络为用户社交网,其是一种典型复杂网络。同时,用户个体决策将会影响其他用户利益。因此,光伏台区用户的需求响应决策过程实质上是复杂网络上的博弈过程。
首先,利用图论方法建立用户社交网模型。节点和连接线是构成社交网络的基本元素,不同节点代表了不同的光伏用户,连接线代表了用户之间存在的社交关系,有连接则表示有社交联系,反之则无,反映了其信息交互关系。文献[14-15]证明了小世界属性和无标度特性是社交网络的2个主要属性。无标度分布是指节点的度分布服从幂律分布。复杂网络的小世界属性是指网络具有较短平均路径长度的同时具有较大的集聚系数。平均路径长度为网络中任意两点之间最短路径长度的平均值。在本文模型中,路径长度体现的是任意2个用户之间进行信息传递所需要经过的用户数量。集聚系数则描述了节点的2个近邻本身是相邻的可能性,即连接在一起的集团各自的邻居中有多少是共同的邻居。
网络聚集系数的计算方法为:假定一个节点i有li个最近邻,Ci为这些最近邻之间实际存在的连接数,则集聚系数qi可表示为:
(1)
对网络中全部节点的集聚系数取平均值,就得到整个网络的集聚系数q:
(2)
因此,考虑到光伏台区用户社交网络的上述属性,本文使用无标度社区网络[16]建立用户社交网络模型,其度分布满足幂律分布,具有小世界属性和社区结构[17-18],可以很好地模拟光伏台区用户之间的信息交互结构。具体的网络生成流程如下:
步骤1:设置初始社区数量M,生成初始m0(m0≥M)个节点,保证每个社区至少有一个节点,初始节点之间完全连接,设置新生成节点数量t0,t=1。
步骤2:网络中加入一个新的节点,在M个社区中等概率随机选择一个进入,记为社区j,它与社区j中的m(m≤m0)个节点建立连接(若社区j中节点数量小于m,则与社区内所有节点相连),连接规则为新的节点与社区j中节点i相连的概率为:
(3)
式中:sij为节点i与社区j内的节点之间的连接度,即建立的连接数量;k为社区j内的全部个体。
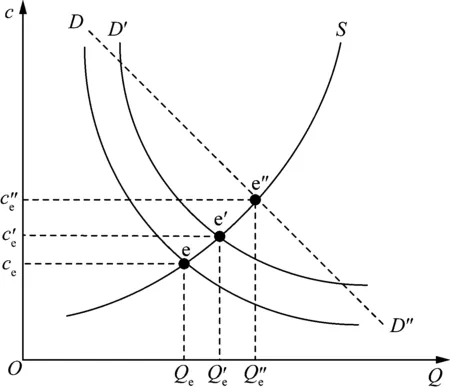
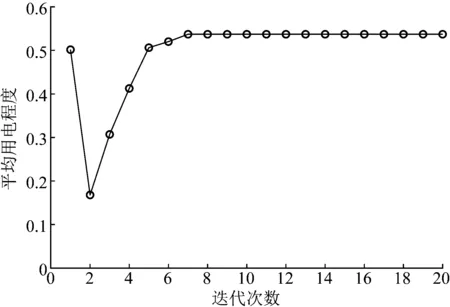
步骤3:判断新的节点是否与外部社区建立连接,建立连接的概率为p(0 (4) 式中:sih为节点i与社区h内节点之间的连接度;n为全部外部社区;l为外部社区中有外部连接的全部个体。 步骤4:t=t+1,当t>t0时停止,否则回到步骤2重复进行。 通过以上步骤进行无标度社区网络的生成,即可得到通过不同聚集特性的用户社交网,其中用户社交网聚集特性由参数p决定,其值越大社交网络聚集特性越明显,对应的集聚系数q也越大。 台区内的光伏用户作为产消者,其生产的光伏电能首先考虑用于自身负荷需求,若有余电,剩余电量由台区统一售卖给电网;若不足以满足需求,则向电网购电以保证负荷运行。台区作为用户的集中器,一方面从配电网购电以满足负荷需求,另一方面将台区内的光伏反向售卖给配电网。作为集中器的台区在发布购售电电价时,其定价策略受到台区整体购售电量的影响,而台区的整体购电量与每一个用户的用电量都直接相关。因此,每个用户的用电决策都可以影响到整体的购售电价格,进而决定了用户的用电成本。基于此,本文建立了光伏台区用户决策演化博弈模型。 当光伏台区作为整体参与到配电网运行调控过程中,为了满足配电网运行需求,作为集中器的台区将通过发布电价以调整用户购售电量。由于用户社群系统中存在信息传播和决策的相互学习,每个用户决策中均会评估和学习与自己有社交关系的其他用户策略,以追求自身利益和满意度。因此,每个用户策略都会受到与其有社交关系的用户的影响,即社交网络反映了博弈关系。建立用户决策博弈模型S={N,{mi},i∈N,{πi},i∈N},其主要包含以下三要素: 1)决策者:台区内N个光伏用户。 2)决策空间:{mi|mi∈[0,1,…,100],i=1,2,…,N}。其中,mi为用户i的用电程度,即用户的实际用电量占用户最大用电量的比例为mi%,其为博弈模型的决策变量。 Qi=mi%Qmax,i (5) 式中:Qi为用户i的实际用电量;Qmax,i为用户i的最大用电量,即忽略用户用电弹性的最大用户需求量。由mi的范围可知,Qi∈[0,Qmax,i]。 根据电价理论和市场的供需关系,电价的制定受到用户整体用电量影响,当整体用电量较大时,电价将会提高以降低用户响应度;反之,用户整体用电需求较低时,电价将会降低,需求改变对市场均衡与价格的影响如图1所示。其中c为电价,Q为需求。这两者之间为复杂的非线性关系,难以用某一确定模型进行描述。 图1 需求改变对市场均衡与价格的影响Fig.1 The impact of changes in demand on market equilibrium and prices 为了能够较为准确地描述供电方(本文指的是作为集中器的台区)的电价制定策略,首先,供电方作为一个具有完善调度决策模式的主体,其为价格的主导者,将根据其自身收益最大化来制定价格。其次,供电方的收益由其成本和售电收入构成。 因此,可以将供电方的定价策略描述为: (6) 式中:c为当前电价;c*为最大化收益时最优电价;Qpv,i为用户i的光伏出力;w0为供电方的收益函数,由式(7)得到。 (7) 式中:Ii、L分别为对第i个用户的售电收益和总生产成本。 供电方的生产成本包括设备投入、原料购买和运营调度成本等,本文使用代价函数[19]来描述。首先做出以下假设:生产成本只与总售电量,即用户的总购电量有关,售电量为0时成本亦为0;生产成本随着购电量的增大而增大;生产电量的单位成本也随着电量的增大而增大。基于上述假设,本文使用二次函数作为代价函数,即: (8) 式中:a和b为与发电成本相关的价格参数,a为二次价格敏感系数,b为一次价格敏感系数,a>0,b>0。 供电方的售电收入即为电价与售电量的乘积,即: Ii=c(Qi-Qpv,i) (9) 此外,还需要考虑电价的上限约束问题: 0≤c≤cmax (10) 式中:cmax为当前时间段内的可取电价最大值。 根据式(6)—(10)所构成的优化问题,可以通过优化算法求解得到最优的决策电价c*,可以看出,c*的大小受到每一个用户的用电量Qi的影响。 3)收益(效用)函数:本文通过用户某一用电程度决策下的用电效用表示。正常情况下,用户i的用电效用πi由三部分构成:购电成本、光伏售电收益和用电满意度大小,其中购电成本和光伏售电收益在假设条件下可以整合为一个表达式,因此πi可以表示为: πi=f(Qi,Q-i)= (11) 式中:Q-i表示除用户i以外,其他用户用电决策,可知单个用户决策收益将受到群体用户决策影响;Si为用户i的用电满意度大小,由式(12)所示的二次效用函数确定[20-21]。 (12) 式中:ω、α为事先设定好的参数,反映用户用电产生的效用大小,用电量越高,对应的用电效用越大,然而其有一个上限值,达到上限值之后,用电量的增加并不会导致用电满意度的提高,更高的ω和更小的α会提高满意度上限。 本文假设所有用户与和自己有社交联系的用户之间存在完全的信息和用电策略共享,考虑到社交网络中信息的传播和用户的相互学习,用户将通过不断更新自身策略以追求自己满意利益。本文采用最优反应学习算法来模拟这种策略调整的动态过程。其基本原理为单个用户通过与社交网络中的其他用户博弈获得收益,即给定前一次的博弈结果,每一个博弈参与者都能够找到最佳的反应策略。具体实现方法为:当用户更新自身博弈策略时,其将自身收益与所有和自己有社交联系的用户收益进行比较,选择其中收益最高的策略作为自身的下一个博弈策略,如此循环迭代直至满足收敛要求。 为了对社交网上的演化博弈模型S进行求解,设计了一种串行求解算法,其主要步骤为: 步骤1:N=1,设置迭代次数N0,设置用户最大用电量、a、b、n、ω、α等。 步骤2:初始化用电策略,即用电程度。 步骤3:根据每个用户用电程度大小计算每一个用户的用电效用πi,通过优化算法更新电价。 步骤4:网络中的每一个用户与和自己具有社交关系的邻居的用电效用进行比较,若均小于自身效用,则下次迭代中策略保持不变;若存在效用大于自己的邻居,则选择效用最大的邻居,将其策略作为下次迭代中的策略,完成策略更新。 步骤5:N=N+1。 步骤6:所有个体同时更新策略。 步骤7:若N>N0,则终止演化博弈,否则返回步骤3重复进行。 所设计的串行求解算法流程如图2所示。 图2 社交网上的演化博弈模型求解算法Fig.2 Algorithm for solving evolutionary game models on social networks 本文考虑由100个光伏用户组成的光伏台区,社交关系通过无标度社区网络[16]生成。社区数量M=3,初始用户m0=3,新增用户数t0=97,内部连接数m=3,外部连接数n=1,外部连接概率p=0.3。生成的无标度社区网络拓扑如图3所示,其中,节点的数字标签为用户编号。由图3可以看出,呈现明显的社区结构,社区之间存在少量连接。 图3 光伏台区社交网络结构拓扑Fig.3 Topology of social network structure in photovoltaic station area 根据文献[22]中某一实际电力系统的价格制定策略,将相关参数设置为:a=3×10-4元/(kW·h)2、b=0.32元/(kW·h)、ω=0.267、α=8.89×10-3,用户的日最大需求负荷电量Qmax,i通过蒙特卡洛模拟进行随机生成,范围为10~50 kW·h;同样地,光伏出力Qpv,i在5~20 kW·h之间。 首先,对社交网上100个用户的用电程度进行初始化,设置迭代次数为100次,每次迭代所有用户都通过第3节的算法流程同时进行策略更新,经过多次重复仿真发现,演化博弈在10次左右达到收敛。因此,取前20次的演化结果,对用户的最终决策(用电程度mi)以20%为粒度进行分组,统计每组的用户数量,计算其所占比例,绘制不同用电程度所占比例的收敛过程,得到的结果如图4所示。 图4 不同用电程度用户所占比例的收敛过程Fig.4 Convergence process of the proportion of users with different participation 另外,统计演化稳定过程中整个台区用电程度的平均值mave的收敛过程,其结果如图5所示。mave的计算方法为: 图5 光伏台区平均用电程度收敛过程Fig.5 Convergence process of average participation in photovoltaic station area (13) 由图4可以看出,用电程度在61%~80%的用户比例从第2次迭代开始就逐渐上升,通过6次左右的迭代演化快速收敛至演化稳定值,并最终占到整体的50%以上;用电程度在81%~100%的用户比例从博弈开始即处于下降状态,达到收敛之后占比几乎为0。由图5可知,整体的用电程度最终收敛至54%左右,代表了整体用电程度的平均水平。因此,在上述参数配置下,大量用户最终通过社交网络进行策略学习与更新,更倾向于选择20%~80%这一区间用电程度的用能策略,整体用电程度较低。 为了更直观地展现在社交网络上用户策略的更新、淘汰和扩散的过程,取第1、3、5、7次演化迭代的结果,用不同颜色表示不同的策略(用电程度mi),演化流程如图6所示。 图6 社交网上的策略演化流程Fig.6 Strategy evolution process on social networks 由图6可知,t=3时,社交网中用户策略取值在0~0.2的比例较高,覆盖了社交网的大部分区域。然而,经过2次迭代之后,策略取值在0.4~0.6的比例急速升高,渗透到每一个社区之中。最终达到收敛之后,每个社区之中均存在占主导地位的占比较高的策略,且各不相同。由此可以看出,由于社交网络具有的小世界属性、效益高的策略会快速沿着社交网络传播,而当出现新的更好的策略之后,原有优势策略又会很快被新策略覆盖。此外,社交网具有社区属性(集聚特性),即不同社区之间集聚特性和网络结构的不同会影响某个优势策略扩散到所有节点,使每个社区或社交群体保持相对独立的策略稳定性。 另外,为了分析稳定性的形成原因,取社交网中相互关联的10个节点进行单独分析,其策略演化流程如图7所示,可以看出达到收敛后,存在2个主要优势策略0.31和0.38,2种策略之间相互接触,然而仍保持策略的稳定性,这种稳定性是由于核心节点S的策略始终不变导致,其在宏观上即反映为社区内部的策略稳定性。 图7 10节点策略演化流程Fig.7 Evolution process of 10-node strategy 社交网络的集聚系数反映了光伏用户之间信息交互的广度以及对应台区内部的社交紧密度和信息传递效率。根据式(1)及式(2),可计算出4.1节生成的社交网络集聚系数为0.215,而分析第1节的模型建立流程可知,社交网的聚集系数主要受节点外部连接概率p的影响。因此为了分析网络集聚系数对演化结果的影响,本文通过设置不同参数p,生成不同集聚系数q的社交网络,用同样的演化博弈方式进行博弈,比较其结果,得到的对比如图8所示。 图8 不同集聚系数的平均用电程度收敛过程Fig.8 Convergence process of average power consumption with different clustering coefficients 由图8可以看出,社交网络的集聚系数越大,其达到收敛之后对应的用户平均用电程度也越大,说明社交网络的小世界属性可以提升用户的用电需求量,提高用户的用电意愿。 由于台区作为集中器参与到电网运行调控时,其需要根据电网需求制定不同的电价,为了分析不同电价制定策略对用户响应结果的影响,本文设置了3个不同参数组合,如表1所示。 表1 不同电价制定策略Table 1 Different electricity-price setting strategies 基于不同的电价制定参数组合,在4.1节中生成的同一个社交网络中进行博弈,其余参数保持不变,得到的平均用电程度演化收敛情况如图9所示。 图9 不同参数组合下的平均用电程度收敛过程Fig.9 Convergence process of average power consumption under different parameter combinations 对于电价二次灵敏系数a,其反映了电价随用户总购电量的变化而改变的程度,由图9中对比组合1和组合3可以看出,a的提高会导致最终平均用电程度mave的降低,这表明用户在用电需求量对电价影响较大的情况下,会更倾向于选择需求量较小的用电策略,光伏用户通过降低自身需求量可以减少向电网的购电量,进而获得更多的光伏余电上网售电收入,这与实际用户的决策情况相吻合。另一方面,对于一次价格灵敏系数b,对比组合1和组合2可以看出,随着b的提高,用户的最终平均用电程度mave相对降低,b对应了当购电量为0时的基础电价,基础电价的升高会导致用户用电意愿的降低。因此,分析结果表明本文所提演化博弈模型的实际可操作性和真实性。对于电网侧,通过分析结果可以判断,通过降低a、b可以提高用户的用电需求,从而促进光伏的消纳。 为了验证本文所构建模型的合理性和有效性,本文借助文献[23]中某实施分时电价需求响应地区在峰时段的2011年8月7日至8月13日连续6天的实际日负荷数据,使用4.1节建立的社交网络模型,根据该地区实际用户情况,设计仿真算例进行本文模型有效性验证。将本文所提方法与弹性系数法、线性分段法、求解复制动态方程法[24-26]以及实际情况进行对比,得到光伏台区用户的用电量结果如图10所示。 可以明显看出,本文所构建的基于社交网上演化博弈需求响应模型从误差和趋势上来看相比于其他方法都更贴近真实的负荷情况,证明了本文所提模型的有效性和合理性,其中与复制动态方程法的对比反映了信息交互对用户响应的影响。而根据图1的分析可知,将用户的需求响应模型线性化之后,会导致供需平衡点上移,对应的电价c和需求电量Q都会升高,这与图10的对比结果也十分吻合,进一步证明了本文所构建模型的合理性。 本文在新型电力系统构建背景下,针对光伏台区用户参与到系统运行调控中响应特征存在不确定性的问题,考虑到有限理性用户对电价或激励措施响应过程中的信息交互以及策略学习特征,提出了一种基于社交网上演化博弈模型的用户需求响应分析模型。通过算例,验证了模型的收敛性,并分析了用户社交网结构和激励电价对用户需求响应决策的影响,可得到如下结论: 1)本文所提考虑用户社群系统影响和用户有限理性特征的基于社交网上演化博弈模型的用户需求响应模型相比传统弹性系数、演化博弈模型等更具有合理性; 2)用户社交网络的小世界属性增强可提高用户的用电需求响应; 3)价格灵敏系数和价格基础系数的提高都会降低用户的用电需求。 本文中,未考虑到社交网络结构随时间的变化以及用户之间社交关系的强弱,对于产消者在不同角色下用电效用计算方法的不同也没有进一步分析。因此,研究社交网结构的动态变化和社交关系的强弱,建立动态加权的社交网络,提出更细化的用电效用计算方法,是接下来的研究重点。2 光伏台区用户决策演化博弈模型
2.1 用户决策模型
-c*(mi%Qmax,i-Qpv,i)+Si2.2 社交网上的信息交互与策略更新
3 模型求解算法
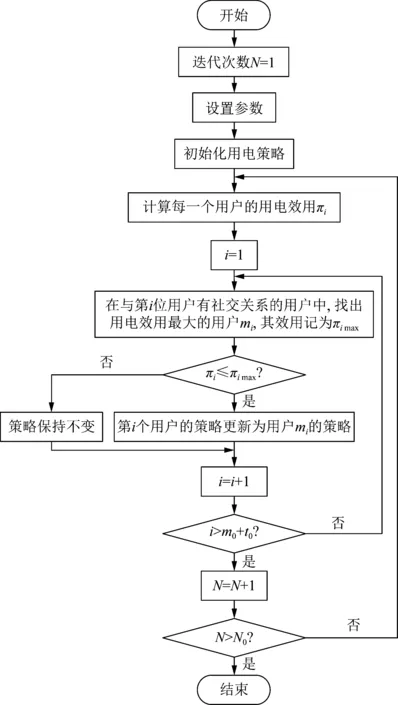
4 算例仿真
4.1 社交网络生成
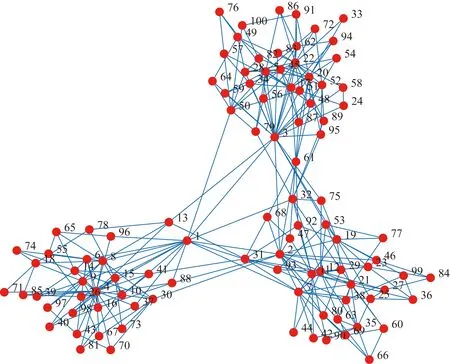
4.2 用户用电响应分布特征

4.3 用户响应策略演化过程
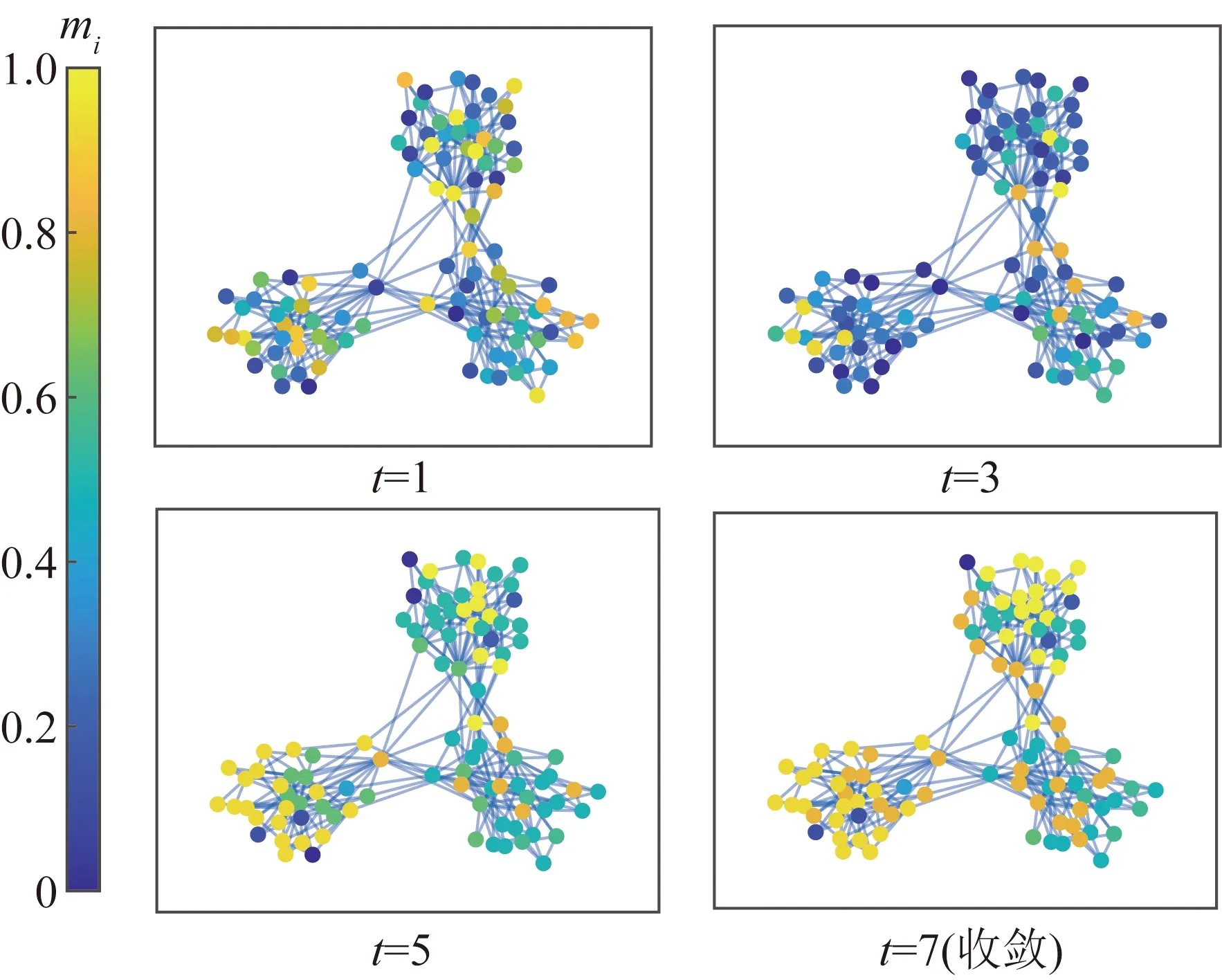
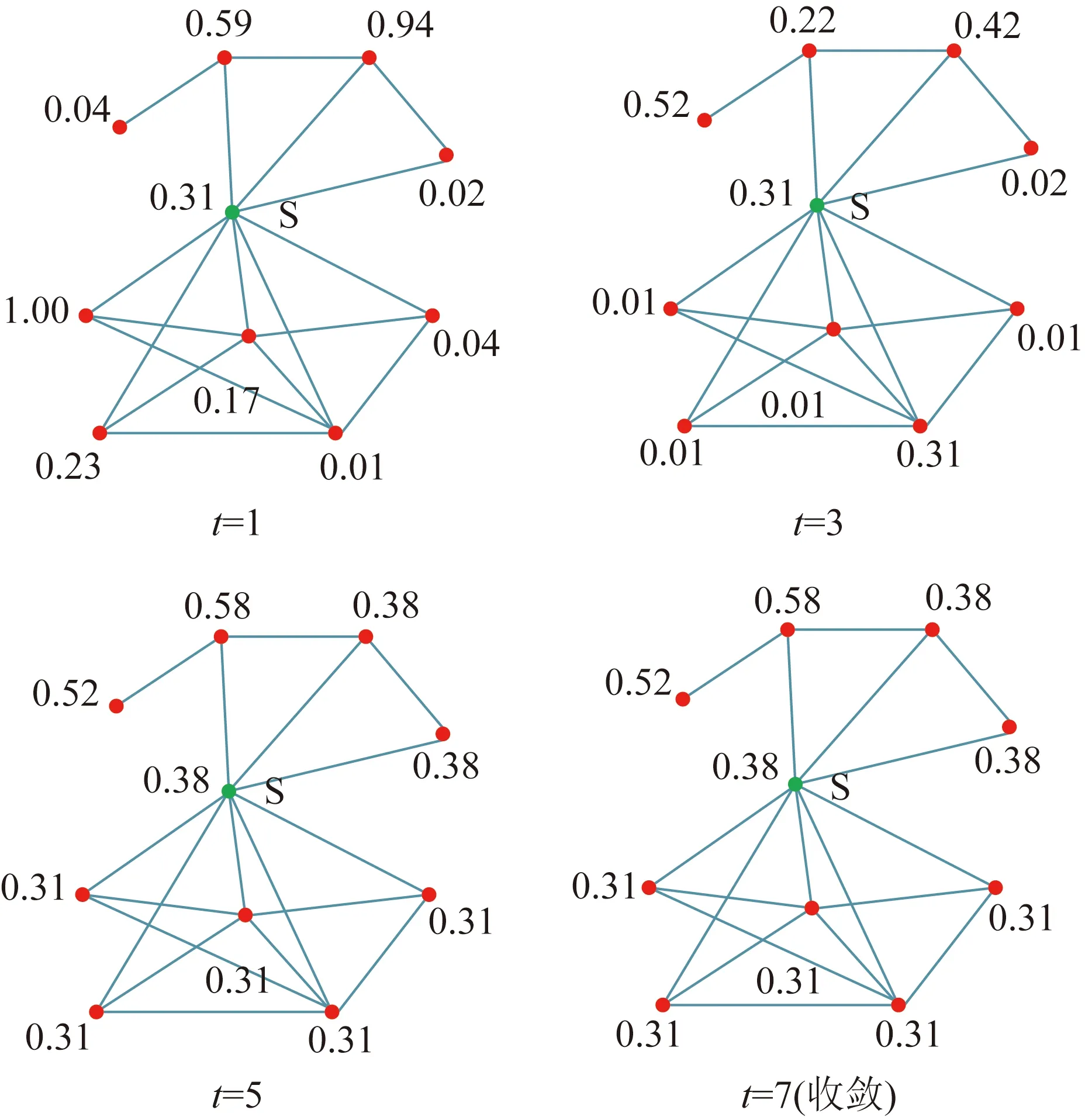
4.4 不同社交网络结构对台区用户整体响应水平影响分析
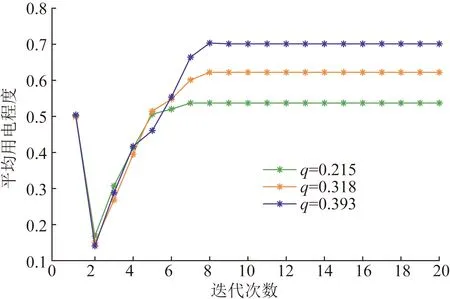
4.5 不同定价策略对台区用户整体响应水平影响分析


4.6 模型有效性验证
5 结 语

