基于扩展移相的双有源桥变换器复合优化控制策略
吕世轩,王俊尧,郑丽君
(煤矿电气设备与智能控制山西省重点实验室(太原理工大学),太原市 030024)
0 引 言
双有源桥(dual active bridge,DAB)DC-DC变换器由于其具有结构对称、电气隔离、高功率密度等优点[1],在固态变压器、直流电网、电动汽车充电桩等场合得到了广泛的应用[2-3]。单移相(single phase shift,SPS)是DAB变换器最传统的控制方式,其基本原理是变压器原副边两侧的H桥分别输出相位不同的方波,通过改变方波之间的相位差从而控制传输功率的方向和幅值,但采用SPS控制DAB在原副边电压不匹配时会出现较高的回流功率和电流应力[4]。
为了解决SPS所存在的回流功率高、电流应力大的问题,扩展移相[5-13](extended phase shift,EPS)、双重移相[14-16](double phase shift,DPS)、三重移相[17-21](triple phase shift,TPS)控制方式被提出。扩展移相和双重移相都有两个自由度,不同之处在于扩展移相仅在变压器原副边其中一侧的H桥加入了桥内移相,而双重移相则是在变压器原副边两侧的H桥均加入相同的桥内移相。自由度的增加使得电感电压波形由之前的两电平波变为三电平波,通过算法合理地配置一个周期内电感电压波形,可以使得电流应力和回流功率大幅减小,优化功率传输效率。为了进一步提高DAB的性能,三重移相在变压器原副边侧加入不同的桥内移相,得到了三个控制自由度。但是,自由度的增加也造成了模式分类困难,切换时工作点不连续和优化算法求解复杂等问题。与其他移相方式相比,EPS自由度较高,且每个开关周期内开关状态不过分复杂,因此本文选择EPS对DAB进行优化。
文献[6]根据DAB不同工作模态电路特性定义了各个模态,阐述了回流功率产生机理,并从原理上解释了EPS回流功率小于SPS的原因,但文献[6]未对回流功率优化算法进行讨论。文献[7]通过建立EPS输出功率和回流功率数学模型,推导EPS下回流功率与移相比及电压传输比之间数学关系,提出一种相同传输功率下回流功率最小的优化算法。文献[8]建立DAB输出电压状态空间平均化模型后,提出一种输出电压模型预测控制,结合梯度下降算法优化回流功率。由于EPS不只有一种模式,但文献[7-8]只在一种模式下进行了分析,无法保证回流功率在全模式下最小。文献[9]则对两种工作模式开展优化,分析了不同电压传输比下传输功率与回流功率耦合关系,解得零回流功率的功率传输域并给出最优回流功率控制策略,但所考虑的模式依然不够全面,因而其给出的零回流功率的区间并不完整。综上,现有回流功率优化策略存在回流功率模型不够全面的问题,继而导致所提控制策略无法充分提升EPS控制效果。
除上述针对EPS回流功率优化策略外,文献[10-12]针对EPS电流应力进行了优化。文献[10]分析SPS和EPS的电流应力模型后,提出了EPS的一种模式下的电流应力优化策略,但由于其所基于的模式不够全面,解得的电流应力仅为该模式下最优解。因此,文献[11-12]在综合分析了更多模式后提出了相应的电流应力优化策略。文献[11]分析了不同模式下的电流应力特性和零电压导通特性,采用KKT(Karush-Kuhn-Tucker)与图像分析结合的方式解得优化算法。文献[12]对模型进行全面分析后,采用拉格朗日乘子法得到全功率范围下最优移相比组合。但以上电流应力优化的文献均为单目标优化,没有同时考虑回流功率和电流应力的影响。
因此,文献[13]提出了一种复合优化策略,该策略通过选择回流功率和电流应力复合优化区间,优化了移相角的选择,但是该策略只考虑了EPS的一种模式,在选择优化区间后也未进一步讨论区间内不同工作点的特性,且无法在线优化。此外,目前的文献仅考虑了电压传输比大于1的情况,对于电压传输比小于1的模型及控制策略均未涉及[7-13]。而电压传输比小于1也是DAB变换器工作情况之一,完成该条件下的数学建模及优化控制策略才能实现DAB变换器的全模式优化,达到最优传输效率。综上,现有EPS的回流功率和电流应力优化方法,存在数学模型不完整、工作模式不全面、优化目标单一、无法在线优化的问题。
针对上述问题,本文提出一种EPS控制的回流功率、电流应力复合优化控制策略,以保证回流功率最小的前提下优化电流应力为目标。首先,建立扩展移相不同模式下的传输功率、回流功率、电流应力的全面的数学模型。然后,基于对各个模式的全面分析选择工作模式,采用有约束极值求解法推导功率控制最优路径。最后,通过实验比较本文所提控制策略、EPS回流功率优化控制策略[5]、EPS优化区间复合控制策略[13]。
1 扩展移相工作模式分析
1.1 扩展移相工作原理
双有源桥DC-DC变换器典型拓扑结构如图1所示,其由高频变压器T、储能电感L、两个稳压电容C1、C2和两个完全对称的H桥构成。图1中:V1、V2分别为变换器两侧直流电压;vh1、vh2分别为两侧H桥输出电压;高频变压器变比为n∶1;定义功率从V1侧传输到V2侧为正方向,定义电压传输比k=V1/(nV2)。

图1 双有源桥DC-DC变换器拓扑Fig.1 The topology of DAB DC-DC converter
图2为扩展移相控制的一种典型工况波形图。图2中,D1为单侧H桥内移相比;D2为双侧H桥桥间移相比;vL为电感瞬时电压;iL为电感瞬时电流;pin为瞬时传输功率;Ths为半个开关周期,Ths=1/(2fs),fs为开关频率。
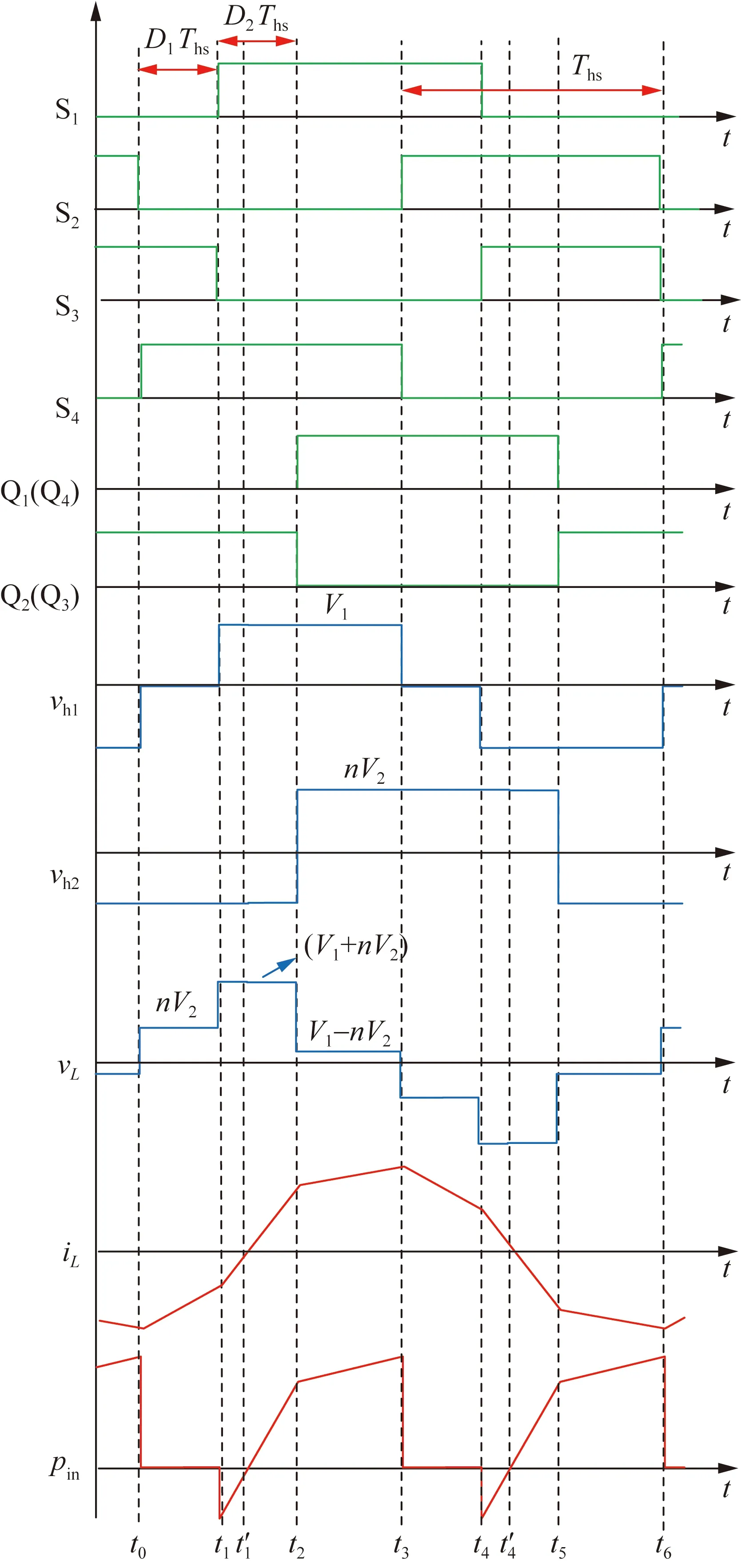
图2 DAB变换器在扩展移相控制下的典型波形Fig.2 Typical waveforms of DAB converter under EPS control
DAB处于稳态时,一个周期内电感电流具有对称性,因此可求解半个周期内平均功率,作为整个周期内的平均功率。图2所示工况下,各个时刻的电感电流值可以表示为:
(1)
根据平均功率公式可得平均功率P为:
(2)
采用单移相控制时的DAB最大传输功率为基准值(PN=nV1V2/(8Lfs)),对式(2)标幺化可得传输功率标幺值p为:
p=P/PN=4D2(1-D2)+2D1(1-D1-2D2)
(3)
该工况在(t1,t′1)内功率反向传输,存在回流功率,对回流功率积分,并采用与传输功率相同的基准值标幺化得回流功率标幺值pbf为:

(4)
由图2得,t3时刻电感电流取到最大值,则电流应力值imax为:
(5)
以单移相控制下DAB最大传输功率时原边侧的平均电流值作为电流应力的基准值(iN=PN/V1=nV2/(8fsL)),对式(5)标幺化得电流应力标幺值G为:
G=imax/iN=2[k(1-D1)+2D1+2D2-1]
(6)
由于不同工况下基于扩展移相调制的DAB的传输功率、回流功率、电流应力表达式均不同,因此首先需要对各种工况下基于扩展移相调制的DAB的传输功率、回流功率、电流应力进行分类与建模。
1.2 传输功率建模
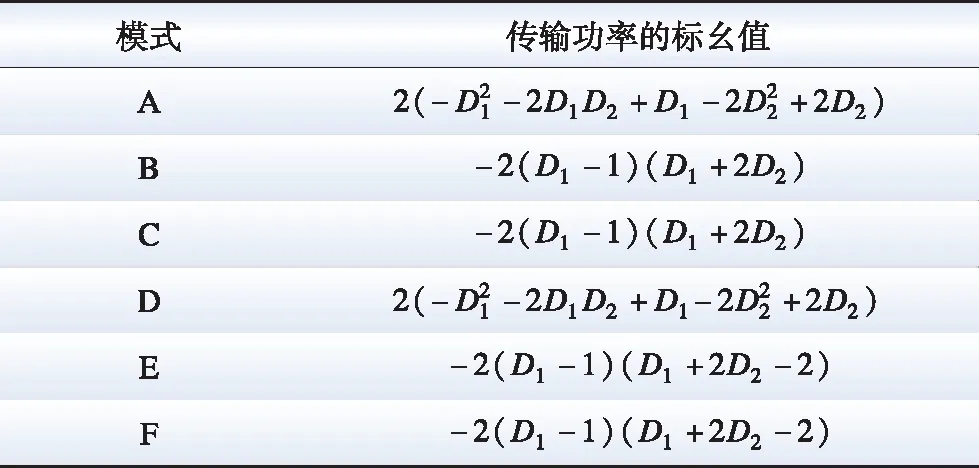
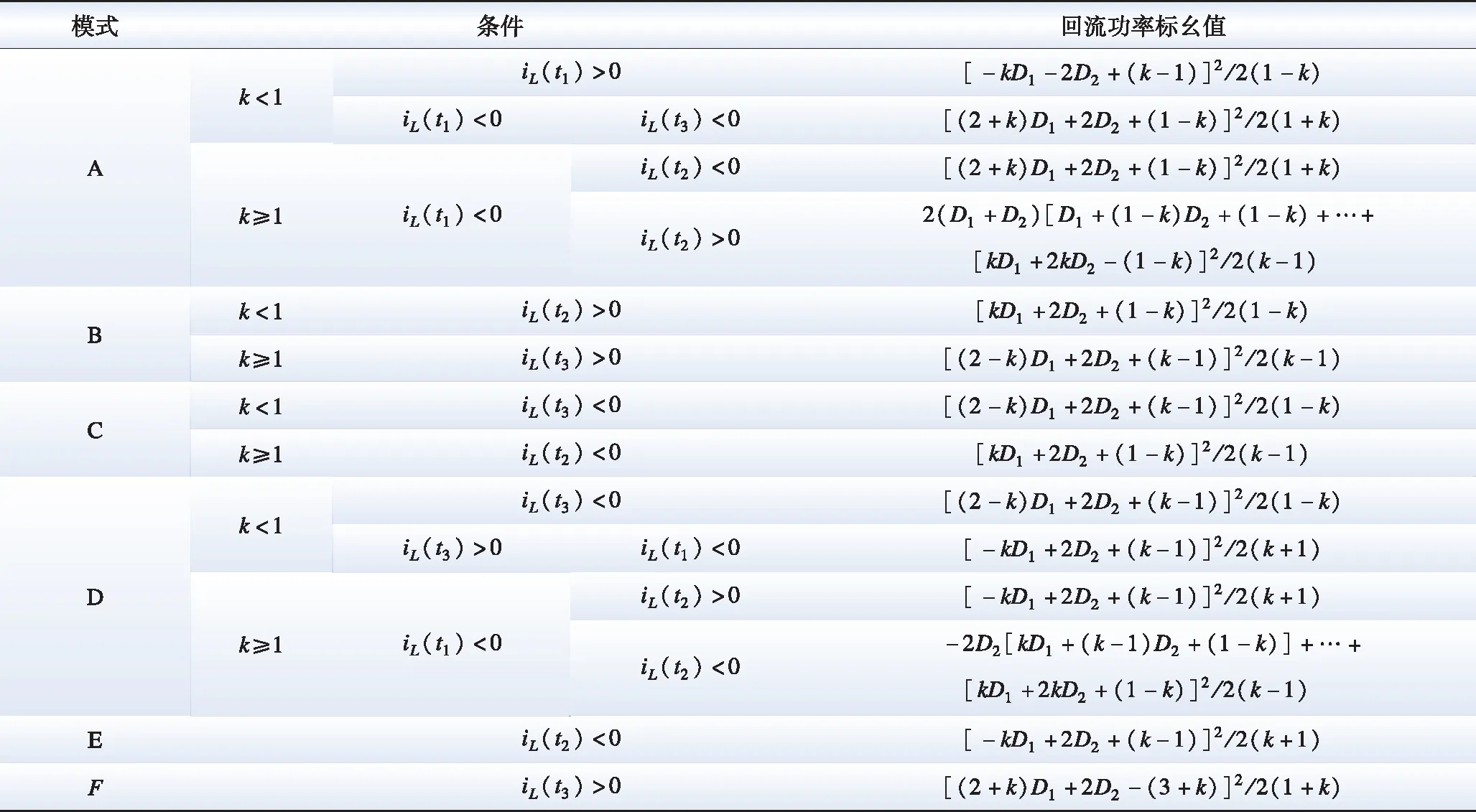
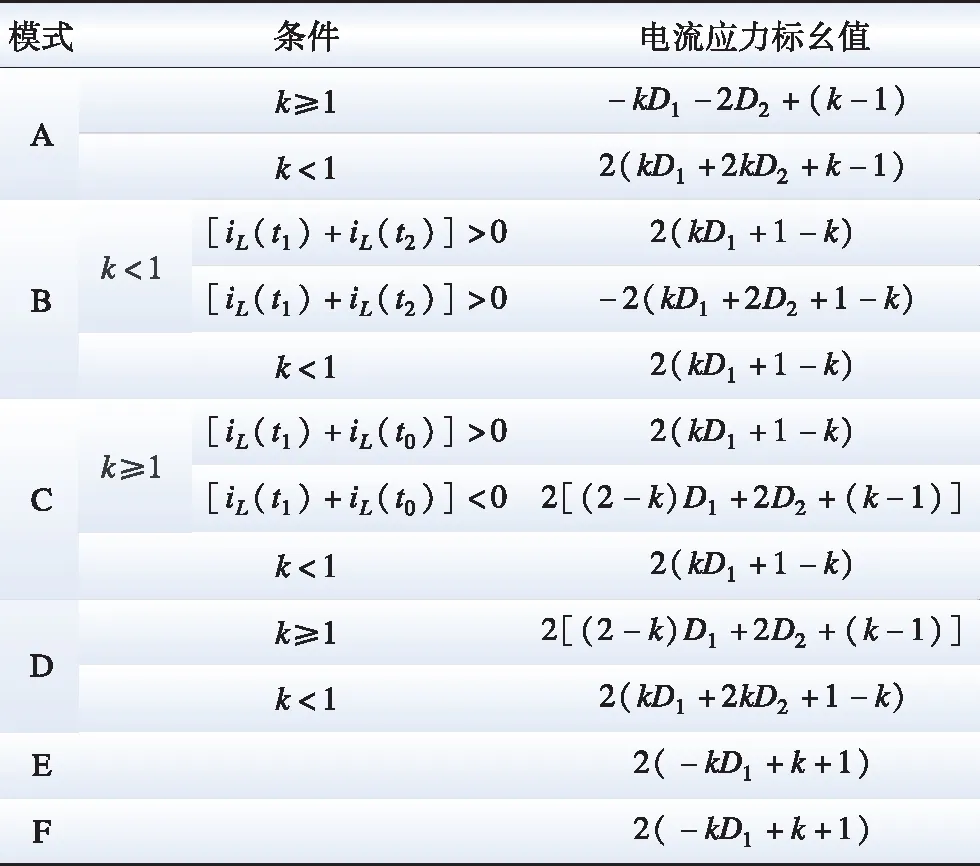
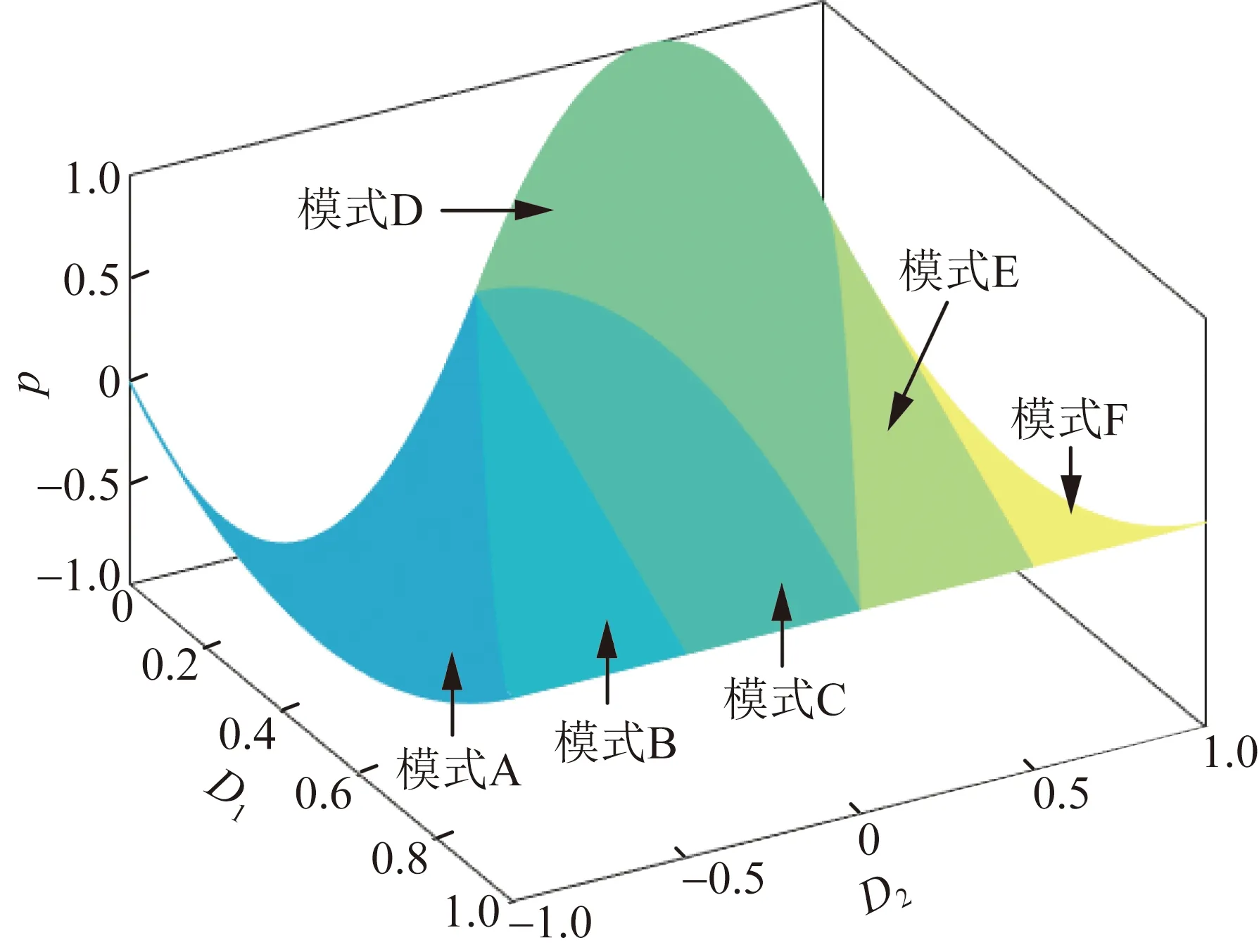
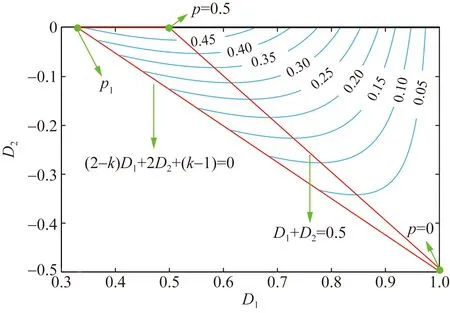
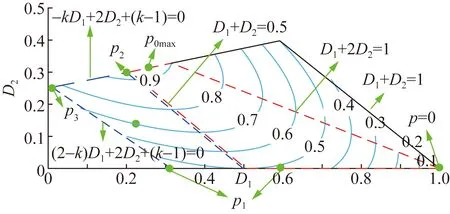
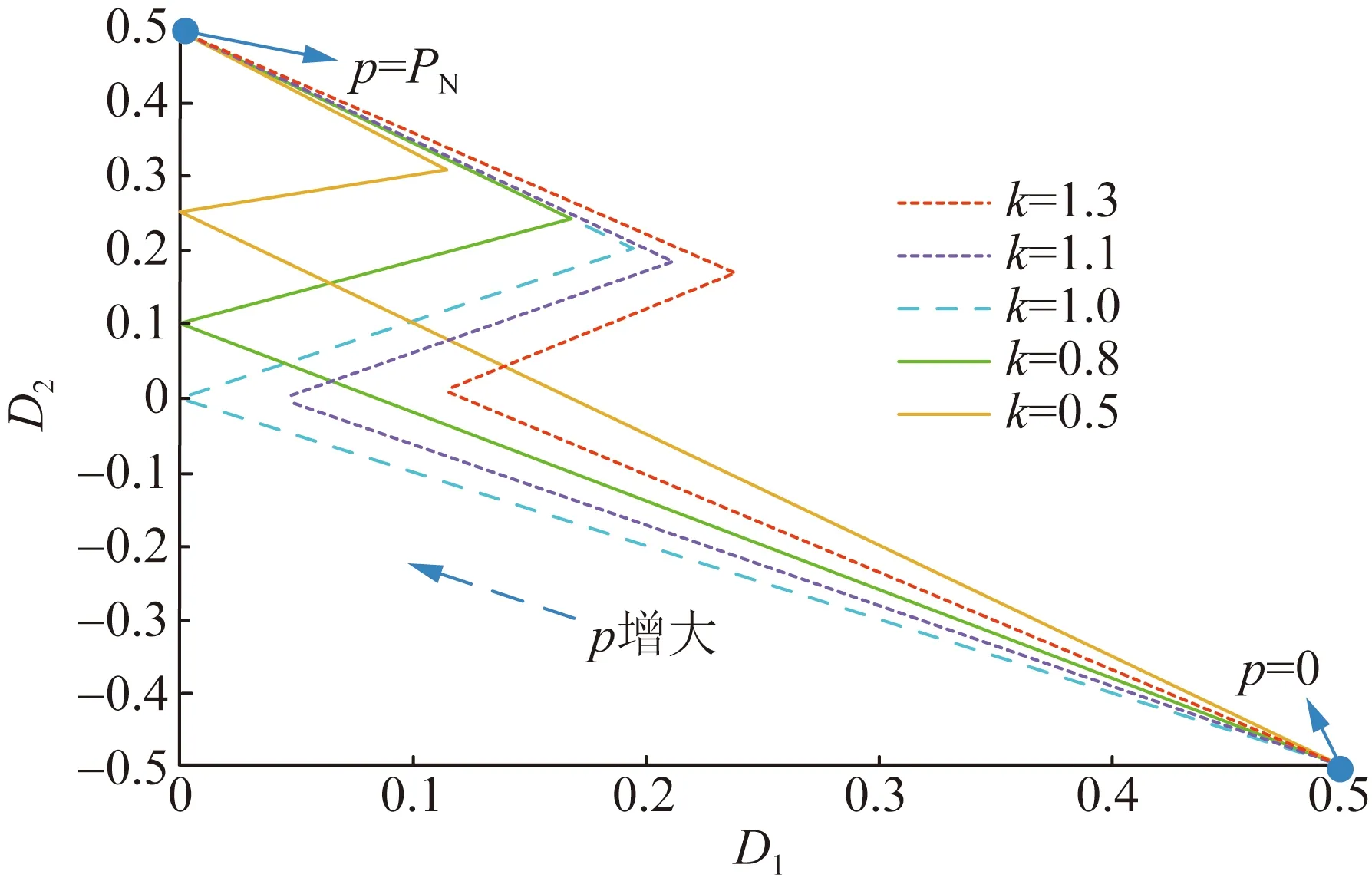
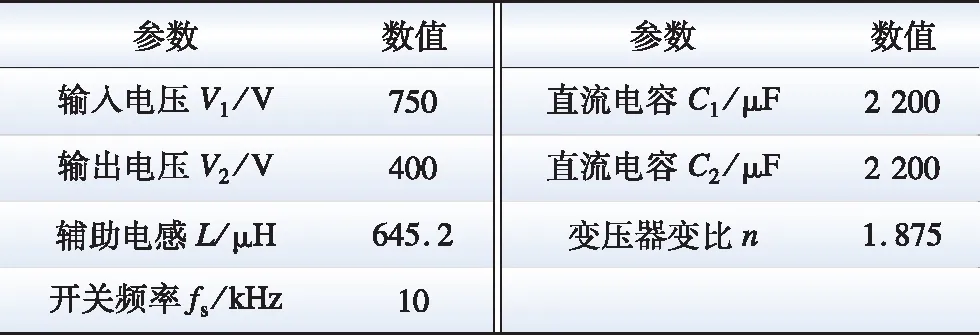
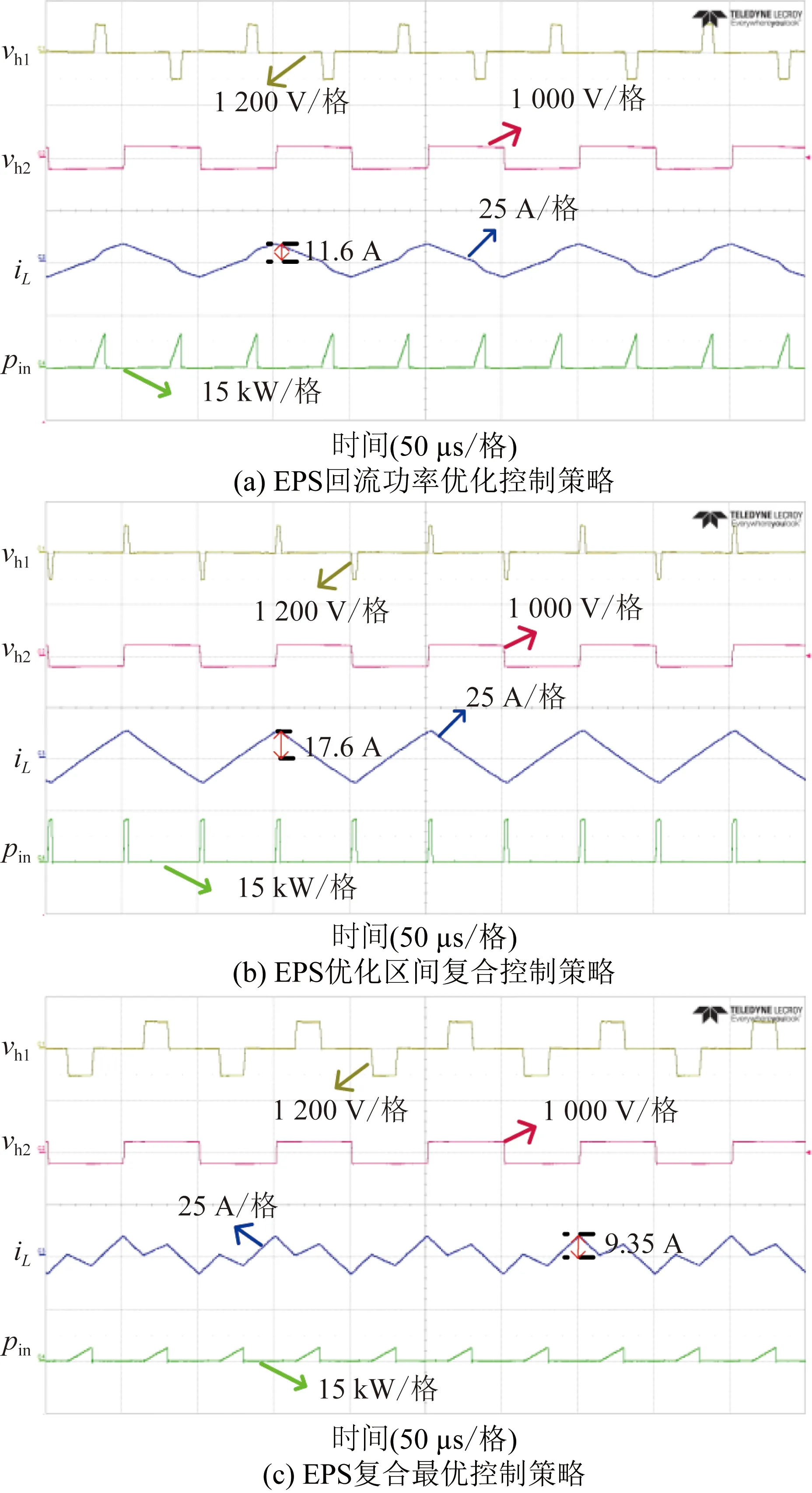
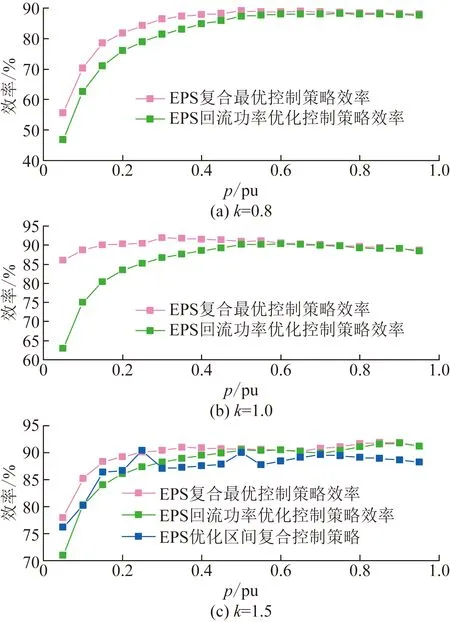
设可行控制域为:0 由图2可以看出,不同的D1、D2组合会影响vh1、vh2、iL的波形,进而影响传输功率。因此,本文根据vh1、vh2之间的相位关系和功率传输方向,将EPS的工作模式分为6种,如图3所示。6种模式的D1、D2组合情况如表1所示。采用与式(1)—(3)相同的求解方法,计算各个模式的传输功率标幺值,各个模式的传输功率标幺值汇总如表2所示。 图3 扩展移相控制工作模式波形Fig.3 Waveforms of six working modes of EPS control 表2 扩展移相控制的传输功率表达式Table 2 Expression of transmission power of EPS control 本节基于EPS传输功率模型分析推导各模式下回流功率的数学模型。通过分析可知同一模式不同工况下回流功率表达式不尽相同,采用与式(1)—(4)相同方式可以解得回流功率,将不同工况下回流功率标幺值pbf的表达式汇总于表3。如表3所示,回流功率的分类条件为k的大小和iL过零点的位置。值得一提的是除表3所示的条件外,其他条件下回流功率为零。 表3 扩展移相控制不同条件下的回流功率表达式Table 3 Backflow power of EPS under different conditions 与回流功率类似,扩展移相的各个模式中的电流应力包含多种情况。通过与式(5)、式(6)相似过程,求解电流应力,并在表4中汇总了不同工况下电流应力标幺值G的表达式,电流应力的分类条件为k的大小和iL过零点的位置。值得一提的是模式E和模式F电流应力表达式相同。 表4 扩展移相控制不同条件下的电流应力表达式Table 4 Current stress of EPS under different conditions 较高的回流功率和电流应力不利于DAB变换器高效运行。回流功率的存在会使功率反向传输,直接降低系统效率,而电流应力则会通过影响变换器导通损耗而间接影响变换器效率。因此,本文以传输相同功率时降低回流功率为首要优化目标,当回流功率相同时,降低电流应力为次要优化目标进行研究,从而提高系统效率。 为此,首先对EPS的传输功率、回流功率、电流应力特性进行分析。为了反映不同模式的传输功率特性,绘制如图4所示的可反映传输功率与移相比D1、D2之间关系的三维曲线图,其中模式C、模式D和模式E为功率正向传输,模式D传输功率域为[0,1],模式C、E则为[0,0.5],其余模式为功率反向传输。由图4可知,扩展移相在功率正反向传输时具有对称性,故本文以功率正向传输时为例分析。此外,由于k≥2在实际情况中极少出现,因此本文主要分析0 图4 扩展移相传输功率三维图Fig.4 3D diagram of the transmission power based on EPS control 模式C、D、E回流功率为零时的传输功率三维图如图5所示。由图5知,模式C、D、E中回流功率为零时最大传输功率点必在模式D内,该点传输功率p0max=2(k+1)/(k2+2k+2),且p0max>0.6。因此,模式D在回流功率为零条件下的传输功率范围为[0,p0max]。而与之相较,模式C、E在回流功率为零条件下功率传输范围仅为[0,0.5]。所以模式C、E回流功率为零时的功率传输域窄于模式D。 图5 回流功率为0时的传输功率三维图(k=0.5)Fig.5 3D diagram of the transmission power when the backflow power is 0 (k=0.5) 模式C、E电流应力三维图如图6所示,由图6可知模式E的电流应力最小值大于模式C的电流应力最大值。 图6 模式C、E电流应力三维图(k=0.5)Fig.6 3D diagram of current stress in mode C and E (k=0.5) 由于模式C和模式E在回流功率为零条件下具有相同传输功率域,而且模式C的电流应力较模式D更小,因此本文选择模式C或D求解优化路径。其中,模式C在回流功率为零的前提下,优化电流应力;模式D在[0,p0max]的传输功率范围内,以回流功率为零作为前提优化电流应力,在(p0max,1] 的传输功率范围内优化回流功率。由于0 由表2可知,模式C内传输功率表达式为: p=-2(D1-1)(D1+2D2) (7) 故传输功率为p0时,模式C内移相比D1有两个解D11、D12: (8) 由表4得,k≤1时模式C电流应力标幺值可表示为: G=2(kD1+1-k) (9) 由于∂G/∂D1=2k>0且D11 (10) 由式(7)—(10)可知,选择D11时,在相同p0下,D2越大,G越小。为了更直观地表示相同p0时D1、D2的组合情况,作出模式C零回流功率区域内传输功率等高线,如图7所示。图7中虚线包围部分为(D11,D2)的可行域,(2-k)D1+2D2+(k-1)=0为回流功率是否存在的分界线,由表3可求得。 图7 模式C回流功率为0区域内的功率等高线Fig.7 The power contour lines of mode C in the area where the backflow power is 0 该可行域内,相同p0下D2随D1的变换趋势可由式(7)关于D1的导数得到,如式(11)所示: (11) 显然在可行域内,dD2(D1)/dD1<0,因此在选择D11传输相同p0时,D1越小,D2越大,相应的G越小。由图7可以看出,在pbf=0区域内,相同p0时D1最小点,即G最小点位于可行域左边界线或上边界线。为了更方便地表示复合最优点随传输功率的变化趋势,定义左边界线(2-k)D1+2D2+(k-1)=0与上边界线D2=0交点传输功率为p1,其值p1=2(1-k)/(k-2)2。 pbf=0条件下,模式C内的电流应力最优路径为: 1)p 2)p1 2.3.1p 为了直观表示模式D内相同p0时D1、D2的组合情况,绘制如图8所示的模式D零回流功率区域内传输功率等高线。 图8 模式D回流功率为0区域内的功率等高线Fig.8 The power contour lines of mode D in the area where the backflow power is 0 图8中,模式D零回流功率区域的边界为D2=0、D1+D2=1、(2-k)D1+2D2+(k-1)=0和-kD1+2D2+ (k-1)=0。其中,D1+D2=1为模式D与模式E的分界线;(2-k)D1+2D2+(k-1)=0和-kD1+2D2+(k-1)=0为模式D内回流功率是否为零的分界线。与模式C相似,模式D的D1也存在两个解,分别如下: (12) 由式(12)可知,D1+D2=0.5为D11和D12的分界线。因此,图8中蓝色虚线区域为D11区域,其余为D12所在区域。并且,D12所在区域覆盖的功率范围大于D11所在区域。为了说明D11和D12所覆盖的功率范围存在差异,定义D11、D12分界线D1+D2=0.5与零回流功率区域分界线-kD1+2D2+(k-1)=0的交点的传输功率为p2=(-k2+4k+4)/(k+2)2。 由图8可知: 1)p1 2)回流功率为零条件下,D11和D12均能覆盖功率范围p1 3)回流功率为零条件下,只有D12能使传输功率达到范围p 针对零回流功率条件下D11和D12所覆盖的传输功率范围的不同,分为两种情况进行电流应力优化。 2.3.2p1 当p1 G=2(kD1+2kD2+1-k) (13) 由于∂G/∂D1=2k>0,为使G尽量小,应选择D11、D12中较小的D11。选择D11后,分析D2对电流应力的影响。根据表2解得D2如下: (14) 由式(14)可知,D1+2D2=1为D21、D22的分界线。因此蓝色区域内,即采用D11的点,所对应的D2均为D21。与前文相似,为了得到该情况下的电流应力最优路径,需求解该区域内相同功率下D21关于D11的单调性和G关于D2的单调性,两者分别如式(15)和(16)所示: (15) (16) 令式(16)等于0,并将所得结果代入式(12)中,可得G的极值点(D1max1,D2max1)表达式为: (17) 由于模式D内D1最小值为0,并且dD21/dD11<0,故D2max1为(D11,D21)区域内D2的最大值。所以,(D11,D21)区域内相同p0条件下G(D2)函数单调。将小于D2max1的数值代入式(16),可得dG/dD2<0。由以上推导可知,在选择D11传输相同p0时,D1越小且D2越大,相应的G越小。故由图8可以看出,传输相同p0时,G的最小点位于(D11,D21)区域左边界线或上边界线。为了说明复合最优点随传输功率的变化趋势,定义左边界线(2-k)D1+2D2+(k-1)=0与上边界线-kD1+2D2+k-1=0的交点的传输功率p3=1-k2。 pbf=0条件下,当p1 1)p1 2)p3 2.3.3p p (18) 由图8可见,-kD1+2D2+(k-1)=0与D1+D2=1的交点所对应的D2为模式D最大D2值,其值D2max=1/(k+2),并且D2max<0.5 在pbf=0条件下,p1 (19) 综上,在选择D12、D21时,传输相同功率条件下,D1越小且D2越小,则电流应力G越小。由此可得,在(D12,D21)区域内,即图8中红色虚线区域内,传输相同p0时G最小点位于可行域下边界线或左上方边界线。 因此,pbf=0条件下p 1)若p 2)若p2 综合模式D下p 1)当p 2)当p1 3)当p3 由表3得,该情况下回流功率标幺值可表示为: pbf=[-kD1+2D2+(k-1)]2/2(1-k) (20) 由于∂pbf/∂D1<0且D11 (21) 令dpbf/dD2=0,可得pbf极点对应的D2值,并将该值代入式(12)中D12的表达式,解得相同传输功率下回流功率最小工作点(D1pbf,D2pbf)的表达式如下: (22) 由式(22)可得(D1pbf,D2pbf)位于直线(k+2)D1+2(k+1)D2-(k+1)=0上,该直线为p>p0max时回流功率优化路径。 为了得到k≤1时全模式下的最优路径,下面对不同功率条件下的各模式最优路径进行分析比较。 1)当p 2)当p1 3)当p3 4)当0.5 1 表5 扩展移相控制复合最优路径Table 5 The compounded optimal path of EPS control 表6 扩展移相复合最优控制策略最优解Table 6 Optimal solution of EPS compounded optimization control strategy 由于所得路径同时受到k与p的影响,变化趋势复杂,因此需要分析所得路径的连续性。当k一定、p不断变化时,工作点随p的改变而改变。此时同一直线上的点必然连续。而对于两条相邻直线转折点处的p,代入表6中由两条不同的直线解得的控制策略中,可以解得相同的工作点,说明所得路径在转折功率时依然连续。例如k≤1,传输p1功率时,在p 由图9可见,随着k不断接近1不同k值下的路径逐渐逼近k=1时最优路径,说明p一定、k不断变化时控制曲线连续。因此,所得控制曲线可以有效防止分界点波动的情况。 图9 不同电压传输比时的控制曲线Fig.9 Control curve under different voltage conversion ratio 根据前文所得的复合最优控制策略,设计了DAB变换器EPS复合最优控制框图,如图10所示。首先采集原副边电压V1、V2和副边电流Io,之后计算得到传输功率p0和电压传输比k。为防因一个周期内p0不断波动而造成控制不稳定,将p0通过低通滤波器得到p0的平均值pofil,与给定功率pref作差后,作为PI环节的输入,根据表6判断当前状态下应采用的复合最优策略,从而在线计算移相比D1和D2。由于控制曲线在不同k、p时均能连续变化,因此采用以上方式可以实现稳定闭环控制。 图10 扩展移相复合最优策略控制框图Fig.10 The control block diagram of compounded optimization strategy 为了验证所提控制策略的有效性,搭建了如图11所示的基于Teledyne Lecroy的DO-D15示波器、Chroma的62150H-1000直流电源、Chroma的63804电子负载的实验平台,实验参数如表7所示。为了体现本文所提控制策略对于功率传输效率的提升,对比了本文所提EPS复合最优控制策略、文献[5]所提EPS回流功率优化控制策略和文献[13]所提EPS优化区间复合控制策略。 图11 实验平台Fig.11 Experimental platform 表7 DAB变换器参数Table 7 Parameters of the DAB converter 当电压传输比k=1.5,传输功率为0.1PN和0.7PN的实验波形分别如图12和13所示。由图12可知,低传输功率时三种控制策略均不存在回流功率。而EPS复合最优控制策略的电流应力为9.35 A,优于EPS回流功率优化控制策略(11.6 A)和EPS优化区间复合控制策略(17.6 A)。故本文所提控制策略在低传输功率时能够使得回流功率为0,且降低电流应力。由图13可知,只有本文所提EPS复合最优控制策略能够使回流功率为零,因此本文所提控制策略可以在高传输功率时降低回流功率,可以增大回流功率为0条件下的传输功率范围。 图12 实验工作波形(k=1.5,p=0.1PN)Fig.12 Experimental working waveform (k=1.5,p=0.1PN) 图13 实验波形(k=1.5,p=0.7PN)Fig.13 Experimental waveforms(k=1.5,p=0.7PN) 为了更好反映不同k下全功率范围内功率传输效率随传输功率变化的趋势,选择k=0.8、1.0、1.5三种情况,每隔0.05PN测量一次原边电源侧发出功率P1与副边电源侧消耗功率P2,规定功率正向传输时,效率η=P2/P1,计算功率传输效率,并将不同k时效率随传输功率的变化曲线汇总,如图14所示。由于文献[13]所提优化控制策略只适用于k>1时,本文只给出其在k=1.5时的实验结果。 由图14可以看出,三种优化控制策略的效率均随传输功率的增大而增大,但本文所提优化控制策略的效率始终优于其他两种控制。EPS复合最优控制策略在k=1时对效率的提升尤为明显。p=0.05PN时,文献[5]所提优化控制策略效率仅有63%,而本文所提优化策略效率为86%,提升了23%;p=0.2PN时,文献[5]所提优化控制策略效率为83.4%,本文所提优化控制策略效率为90.3%,效率的提升虽然不如p=0.05PN时明显,但也有小幅提升。k>1时,本文所提控制策略也依然效率较高,在p=0.1PN时,效率为85.7%,而EPS回流功率优化控制策略和EPS优化区间复合控制策略则分别只有80.2%和79.6%。实验结果表明,相较于其他优化控制策略,本文所提优化策略在不同k值时均提升了DAB变换器的传输效率,在低传输功率时尤为明显。 图14 不同控制策略的效率对比图Fig.14 The comparison of efficiency under various control strategies 本文对DAB变换器在EPS控制下的各个模式的传输功率、回流功率、电流应力进行了全面的分类与建模。以所得数学模型为基础,提出了一种回流功率和电流应力复合优化控制策略。将所提控制策略与EPS优化区间复合控制策略、EPS回流功率优化控制策略进行了实验对比,理论分析和实验结果表明: 1)相比于现有EPS优化控制策略,所提控制策略采用多种工作模式组合的方式,增大了回流功率为0条件下的传输功率范围。 2)所提控制策略在实现零回流功率的前提下,对电流应力进行了优化,从而进一步提升了DAB变换器的功率传输效率。 3)本文所得的EPS控制策略在各工况下复合最优路径清晰直接,便于工业应用与数字化实现。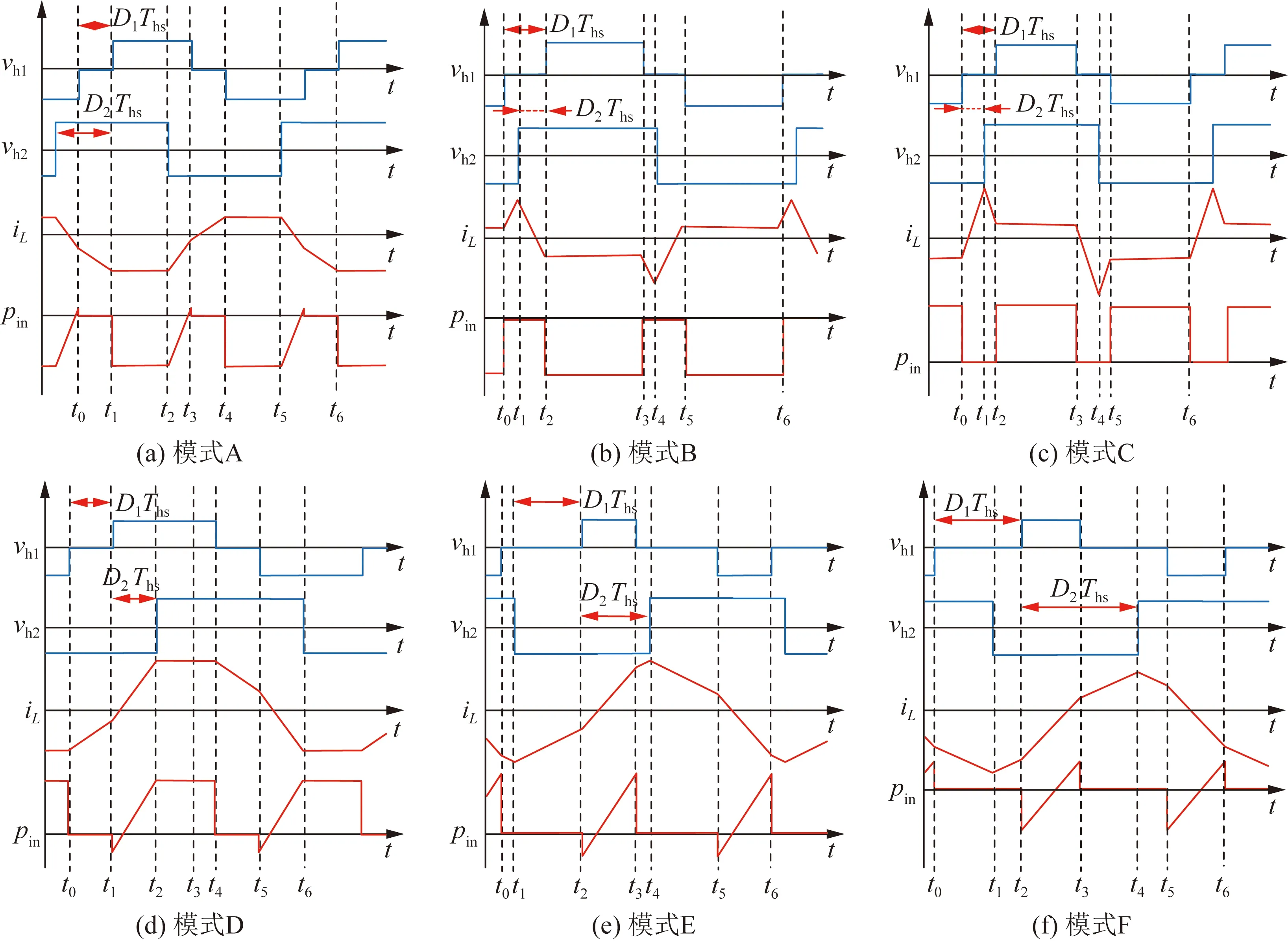
1.3 回流功率建模
1.4 电流应力建模
2 各模式内的最优路径
2.1 复合优化控制策略设计思路


2.2 模式C内的最优路径
2.3 p

2.4 p≥p0max时模式D内的优化路径
3 EPS复合最优路径


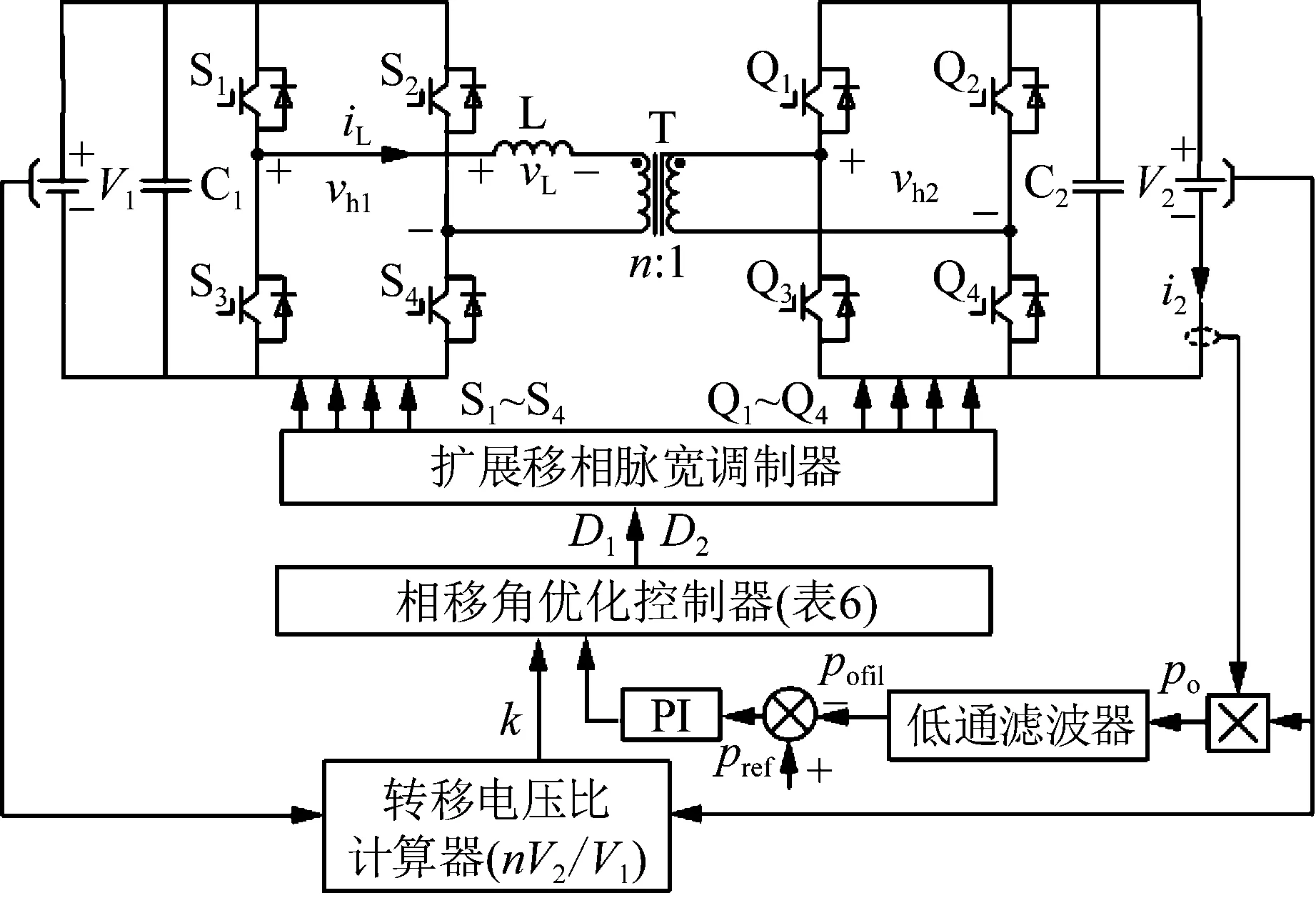
4 实验验证
4.1 复合最优策略的验证方式

4.2 工作波形分析

4.3 功率传输效率分析
5 结 语

