基于拓展移相控制的双有源桥全软开关模态的最小回流功率控制
许崇福,张纬晨,陈干,李怡初,王丰
(1.西安西电电力系统有限公司,西安市 710075;2.西安交通大学电气工程学院,西安市 710049)
0 引 言
20世纪90年代初期,双有源桥(dual active bridge,DAB)DC/DC变换器被第一次提出。由于具有高功率密度、低损耗、双向功率流动、便于模块化等优点,DAB变换器在电力能量转换的应用中受到越来越多的关注[1],例如直流微电网[2-6]、分布式发电系统和混合系统[7-14]等。
DAB变换器最基本的控制方法是移相控制。该策略下,通过控制DAB电路两侧全桥的方波电压移相比来控制DAB电路的功率传输特性。根据移相角数量的多少,传统的移相控制主要可分为单移相(single phase shift,SPS)控制和双移相(double phase shift,DPS)[15]控制。单移相控制实施较为简单,已广泛应用于工业DAB变换器的控制中[16]。但在单移相控制下,DAB变换器可控自由度较低且性能较差,尤其当隔离变压器的输入和输出电压严重不相等时,存在严重的功率回流与高电流应力现象[17]。这种情况会导致器件成本增加,拓扑效率低下,甚至会引起DAB变换器中功率器件的损坏[18]。为了克服单移相控制的上述缺点,文献[18]提出双移相控制方案来消除无功功率,同时减少电流应力,提高效率。文献[19-20]讨论了双移相控制的传输功率特性和动态特性,提出将双移相控制方案与优化补偿应用于DAB变换器,以减少无功功率和电流应力[21]。在此基础上,文献[20-22]提出了拓展移相(extended phase shift,EPS)控制下的最小回流功率方案。然而,当回流功率下降,传输功率明显下降,整个拓扑的效率变化无法正确判断[22]。文献[23]提出了一种新颖的DC/DC变换器,减少了开关管和门极驱动器的数量。文献[24]提出优化一次侧和二次侧之间的导通角和相移的方法,可以最小化回流功率有效值和峰值电流,确保在较宽工作范围内实现最高效率。文献[25]提出了一种混合控制,通过一次侧脉宽调制和二次侧移相调制得到了最小峰值电流控制曲线。文献[26]提出通过最小化电流应力有效值来最小化传输损耗。根据功率水平不同,采用不同的优化方法来保持恒定的功率传输。文献[27]给出了一种效率优化方法,通过一次侧和二次侧的零电压开通来降低传导损耗。文献[28]提出了一种封闭式的解析方案,在整个工作范围内为开关管的非线性寄生输出电容充电,而实现零电压开通。然而上述现有的控制方法对回流功率的降低并不彻底,并且难以实现在维持输出电压恒定的同时,降低回流功率和电流应力等优化目标。
本文在拓展移相控制的基础上,确定能实现全部开关管软开关的边界条件,能够极大降低开关损耗;并且提出一种新型的回流功率优化技术,有效降低回流功率。另外,设计一套闭环控制系统,通过负载的连续投切,证明该方法在线控制的可行性。
1 DAB变换器特性分析
DAB变换器拓扑结构如图1所示。DAB变换器由2个对称的全桥电路、一个高频变压器T和一个电感L组成。高频变压器T实现了原边和副边之间的电流隔离。移相电感L由高频变压器漏感和辅助电感组成。一般认为变压器的励磁电感很大,故变压器的该支路可视为开路状态。输入电压为V1,输出电压为V2。高频变压器T的匝数比为n,移相电感L对功率传输和能量存储具有重要影响。

图1 DAB变换器拓扑Fig.1 The topology of a DAB converter
DAB变换器运行时,电流应力峰值会导致开关管结温升高并且会对开关管产生较大的电流冲击。因此必须限制回流功率和电流应力的影响。这里设开关管Q1和Q4的触发脉冲间的移相比为D1,为内移相比。开关管Q1和Q5的触发脉冲之间的移相比为D2,为外移相比。对于EPS控制,回流功率Pbackflow被有效地限制。
图2为DAB变换器在拓展移相控制下的等效电路。当V1>nV2时,EPS控制下DAB的波形如图3所示。n为变压器变比。在发射功率P的瞬态波形中,面积A代表回流功率Pbackflow,面积A和B之和代表输入功率P。

图2 D2 图3 D2 根据等效电路,原边交流输出电压可等效为三电平电压源Vh1,副边交流输出电压可等效为电压源Vh2。由于原边和副边的交错影响,电感电流iL在t4时达到峰值G1,在t5时达到峰值G2。在半个开关周期Ths内,电感电流iL的峰值iLmax可表示为: iLmax=max{G1,G2} (1) 由于输出电压存在波动,很难保持其恒定。为了评估输出侧电压波动的情况,引入了电压转换比k的概念: (2) 当电压转换比k>1时,DAB工作在降压Buck模式。当k<1时,DAB工作在升压Boost模式,当k=1时,DAB的效率和软开关面积是所有工作状态中最高的。 在EPS控制下,为保证DAB变换器工作于Buck模式,需使得外移相比D2小于内移相比D1。此时DAB的输入功率P可表示为: (3) 式中:fs为开关管开关频率;L为电感。 电感电流iL的峰值G1和G2分别可表示为: (4) (5) 为了保持电感L内部的能量平衡,需要保证电感电流的峰值过零。在这种情况下,需使得G1和G2的值均大于零,表示为如下不等式: (6) 结果表示为: 0≤D2≤0.5 (7) (8) 其中当t等于t3时,电感电流iL变为零。 对于该条件下的DAB变换器,电流应力约束条件可以表示为:i(0)<0,i(1)>0,i(2)<0;操作边界可以表示如下: (9) 图4详细阐述了DAB变换器在拓展移相控制下一个周期内电感电流iL、Vh1和Vh2的瞬态波形。 图4 EPS控制下的iL、Vh1和Vh2波形Fig.4 Waveforms of iL,Vh1 and Vh2 under EPS control DAB拓扑在EPS控制下一个开关周期内各模态拓扑特性如图5所示。 下面为各模态详细过程。其中Di表示开关管Qi的反并联二极管,其中i=1,2,…,8。 模态1:图5(a)为DAB变换器模态1的等效电路。t0之前,Q2和Q3开通。在此期间,Vh1等于V1,Vh2等于-nV2。一次侧Q3非零电压关断,Q2和D1开通。电流iL为负方向。二次侧反并联二极管D6和D7开通。 模态2:图5(b)为DAB变换器模态2的等效电路。在此期间,Vh1等于0,Vh2等于-nV2。一次侧Q1零电压开通,Q2零电流关断。电流iL向正方向变化。二次侧Q6和Q7零电压开通。 图5 ZVS区域DAB各工作模态特性Fig.5 Characteristics of each working mode of DAB in the ZVS area 模态3:图5(c)为DAB变换器模态3的等效电路。这时,Vh1为0,Vh2等于nV2。一次侧Q1和D2继续开通。电流iL保持正方向。二次侧Q6和Q7不能零电压关断。同时,D5和D8开通。 模态4:图5(d)为DAB变换器模态4的等效电路。在此期间,Vh1为0,Vh2等于nV2。一次侧Q1和D2仍然开通。电流iL保持正方向。二次侧Q5和Q8零电压开通。 模态5:图5(e)为DAB变换器模态5的等效电路。此时,Vh1等于V1,Vh2等于nV2。在一次侧,Q2不能零电压关断,D1仍然保持开通。同时,D4开通。电流iL向负方向变化。在二次侧,Q5和Q8仍然开通。 模态6:图5(f)为DAB变换器模态6的等效电路。在此期间,Vh1等于V1,Vh2等于nV2。在一次侧,Q1和Q4零电压开通。电流iL向负方向变化。二次侧Q5和Q8在没有零电压的情况下关断。同时,D6和D7同时开通。 模态7:图5(g)为DAB变换器模态7的等效电路。在此时期,Vh1等于0,Vh2等于nV2。在一次侧,Q1在没有零电压的情况下关断,D1保持开通。电流iL保持负方向。在二次侧,D5和D8保持开通。 模态8:图5(h)为DAB变换器模态8的等效电路。在此期间,Vh1为0,Vh2等于nV2。在一次侧,Q1零电压开通,Q4零电流关断。电流iL保持负方向。在二次侧,Q5和Q8零电压开通。 模态9:图5(i)为DAB变换器模态9的等效电路。在此时期,Vh1为0,Vh2等于-nV2。在一次侧,Q3和D4保持开通。电流iL保持负方向。二次侧Q5和Q8在没有零电压的情况下关断。同时,D6和D7开通。 模态10:图5(j)为DAB变换器模态10的等效电路。该时间内,Vh1为0,Vh2等于-nV2。一次侧,Q3零电流关断,Q4零电压开通。电流iL向正方向变化。在二次侧,Q6和Q7零电压开通。 模态11:图5(k)为DAB变换器模态11的等效电路。在此模态内,Vh1等于-V1,Vh2等于-nV2。在一次侧,Q4不能零电压关断,而D2开启。电流iL保持正方向。二次侧Q6和Q7保持开通。 模态12:图5(l)为DAB变换器模态12的等效电路。在此期间,Vh1等于-V1,Vh2等于-nV2。在一次侧,Q2和Q3零电压开通。电流iL保持正方向。在二次侧,Q6和Q7零电流关断。 这种控制策略可以实现所有开关管开通过程的全工作区零电压。开关损耗为所有开关管关断过程的硬开关造成。 基于DAB的拓展移相控制,将内移相比D1和外移相比D2作为优化变量,以等式约束和不等式约束作为拉格朗日乘数法的边界限制条件,进而得到拉格朗日函数: L(D1,D2)=Pbackflow+λ1P+μ1g1+ μ2g2+μ3g3 (10) 式中:g1、g2、g3为式(9)所示不等式条件;λ1、μ1、μ2、μ3为拉格朗日乘子。 根据公式(10)可知,拉格朗日乘数法将回流功率与电流应力有边界的优化问题转化为了无约束条件的方程组问题。设x指代变量(ΔD1,ΔD2,D1,D2),根据卡罗需-库恩-塔克最优化条件可知: (11) 不等式约束的系数满足如式(12)的基本关系,由μi≥0,λi≤0可知: (12) 根据公式(12)可推导得: μigi=0 (13) 根据公式(13)可简化公式(11): minL(x,λi,μi)=minPbackflow (14) 对公式(14)中的每一个变量求偏导,对拉格朗日函数求解极小值点就可以得到DAB电路最小回流功率的工作点。根据所得结果控制内外移相比D1和D2,进而生成开关管Q1—Q8的驱动信号,即可完成DAB变换器的拓展移相零回流功率控制。 为验证上述拓展移相零回流功率控制理论的可行性,搭建了DAB实验平台进行实验验证。DAB电路的实验平台如图6所示,平台主控制器采用TMS28377 DSP,开关器件选择英飞凌的MOSFET IPB072N15N3G。DAB主功率电路由两层H桥、一个隔离变压器和一个电感组成。 图6 DAB变换器的实验平台Fig.6 The experiment platform of DAB converter DAB电路实验平台各器件参数如表1所示。 表1 DAB电路实验参数Table 1 Experiment parameters of the DAB converter 所得实验波形如图7所示。波形从上至下依次为副边交流电压、原边交流电压、DAB变换器瞬时功率、电感电流。其中,变换器瞬时功率x轴下方为回流功率。 从图7可以看出,初始运行状态下,存在明显的功率回流现象。但当运行在最小回流功率点时,回流功率有了明显的降低。另外,在不同控制策略下分别测试了DAB变换器效率。经整理后的效率对比如图8所示,其中拓展移相控制1为D1=0.1、D2=0.1,拓展移相控制2为D1=0.2、D2=0.1,拓展移相控制3为D1=0.3、D2=0.1。 图7 实验结果波形Fig.7 Waveform from experimental result 图8 不同控制策略效率对比Fig.8 Comparison of the efficiency of different control strategies 由图8可以看出,在最小回流功率控制下DAB变换器拓扑效率较拓展移相控制有明显提高。 从上述分析及实验结果中可以看出,当D1=D2,k>2时,回流功率可以降为零。基于该控制策略的闭环控制器结构框图如图9所示。其基本原理为:采样DAB变换器输出电压,将其与参考电压相减后经过PI调制器,得到可控制变量:内移相比D1与外移相比D2,通过PWM调制器输出原副边开关管门极脉冲。 图9 闭环控制器结构框图Fig.9 Regulator structure diagram of closed-loop control 为了验证上述结论在连续负载投切情况下的稳定运行能力,在Matlab/Simulink中搭建仿真模型。为验证其动态特性,分别在0.5 s、0.9 s和1.5 s设置负载旁路、投切,所得仿真波形分别如图10和图11所示。图10为副边电压、电感电流、输出电压动态变化,图11为输出电压波形。 图10 动态变化波形Fig.10 Dynamic variation waveforms 从仿真波形结果可以看出本文所提出的零回流功率控制具有良好的动态特性。在负载连续旁路的工况下,输出电压能够迅速恢复到原先的电压水平。 在拓展移相控制下,本文通过对开关管电流应力的约束,提出了DAB变换器开关管全工作范围软开关实现的边界条件;另外,通过拉格朗日函数求解极值,得到了一种新型回流功率优化控制策略。在此控制策略下,DAB工作的回流功率被极大地降低,甚至在某些工况下实现零回流功率,提升了DAB变换器在拓展移相控制下的运行效率。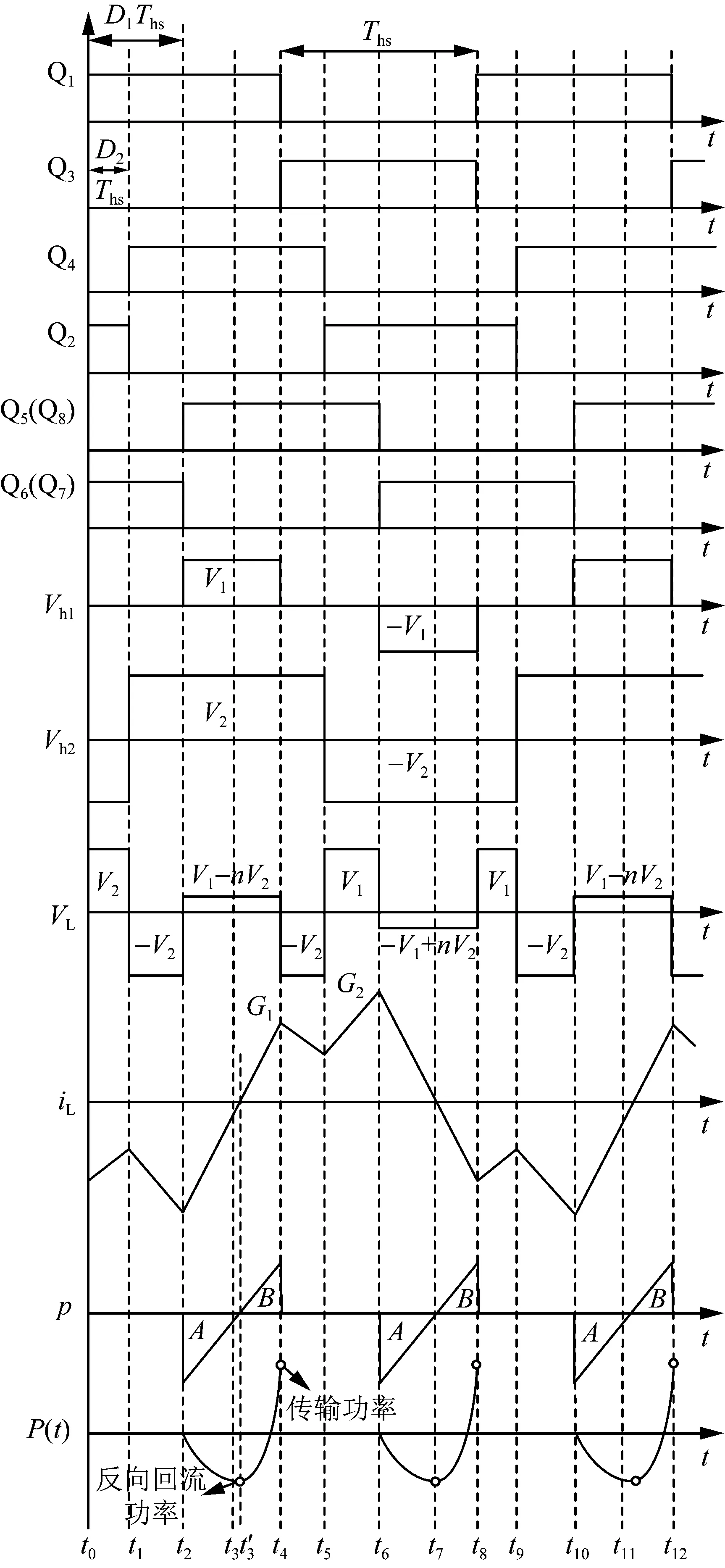

2 全软开范围分析


3 回流功率优化分析
4 实验验证




5 控制器结构设计


6 结 语

