基于价值认同的需求侧电能共享分布式交易策略

詹祥澎,杨军，沈一民，钱晓瑞，王昕妍，吴赋章

(1.国网福建省电力有限公司营销服务中心，福州市 350011；2.武汉大学电气与自动化学院，武汉市 430072)

0 引 言

随着主动配电网的发展，电力需求侧出现了大量的灵活资源，例如分布式电源、储能设备和柔性负荷等[1-2]。海量灵活资源的集成使得电力用户由“消费者”向“产消者”转型[3]，推动其由传统负荷属性衍生出商品属性，进而孕育了电能共享这一新型电力市场模式[4]。电能共享交易在大规模、小容量电能互动中具有巨大的潜力，有望降低交易成本并促进电力资源的优化配置[5]。为此，本文针对电能共享市场的交易机制进行研究，旨在提升电能共享市场的有序性、高效性和灵活性。

不同于现有的集中电力交易模式，电能共享模式放宽了参与主体的容量门槛，使得灵活资源能够以产消者的身份参与电能交易[6]。产消者能进行直接交易，而不依赖于电力交易中心，免去了复杂的交易流程并大大减小了交易成本[7]。但另一方面，灵活资源同时具有调整负荷与发电的能力[8]，能够在生产者与消费者之间自由切换，形成了复杂的供求关系，使得电能共享市场存在无序竞争的风险。为此，不少学者针对电能共享市场的交易问题进行了研究。文献[9]假设产消者形成了联盟并集中优化生产消费计划，进一步基于Shapley值分配收益。文献[10-11]同样基于合作博弈研究电能共享模式，并需要一个调度中心协调产消者的电能计划。然而产消者间通常难以形成稳定的联盟关系，若联盟中的部分个体存在过大的市场权利，其将表现出投机、垄断等市场作恶行为，导致了联盟关系的破裂。因此，若缺乏合适的再分配机制，产消者之间将形成非合作博弈关系[12]。其中，文献[13]将虚拟电厂视为领导者，基于主从博弈描述了虚拟电厂与产消者的非合作博弈关系，然而在该模式下产消者作为价格接受者而不具备市场权利，限制了产消者参与电能共享的积极性。对此，文献[14]提出了一种拍卖模式，允许产消者独立申报价格并由电力交易中心完成市场出清，形成了Nash-Stackelberg博弈，但其复杂的交易机制带来了高昂的交易成本。为了简化交易流程，文献[15]将产消者分为生产者与消费者，建立了由生产者报价而消费者报量的电能共享交易模式，形成了Nash-Stackelberg-Nash博弈，实现了产消者间的去中心化交易。然而该模式需要产消者提前确定其在电能共享市场中的身份，限制了产消者的灵活性。为此，文献[16]提出了一种基于广义供求函数的电能共享策略，在该模式中产消者优化各自的供求偏好并与其他产消者形成了广义纳什博弈，通过求解该博弈的一般纳什均衡能够获得电能共享市场的出清结果，但仿真结果表明其无法实现社会福利的最大化，仍有待进一步改进。

为解决现有研究的不足，本文主要完成了以下创新工作：

1)提出一种新颖的分布式交易模式，具有扁平化、轻量化和低交易成本等特征，适用于点多量小的需求侧电能互动，为“隔墙售电”和新能源消纳提供新思路，能够解决电力市场化交易的“最后一公里”问题。

2)提出基于一致性协议的价值认同机制，剖析“信息”这一生产要素在电力市场化交易中的作用，利用信息物理网络完成了价格信号的传递与认同，打破产消者间的信息壁垒，实现电力资源的优化配置。

1 电能共享模式与博弈均衡分析

如图1所示，在传统电力市场模式下，产消者根据自身设备的状态分别进行决策，并通过电力交易中心完成交易申报。在该模式下，产消者的决策空间较小，且面临复杂的交易流程和高昂的交易成本，往往被迫以自发自用或全额上网方式运行，无法发挥需求侧资源协调互补互济的优势。

图1 需求侧电能共享示意图Fig.1 The diagram of power sharing at demand side

需求侧电能共享模式则被定义为：拥有闲置电能的一方有偿暂时让渡电能使用权给另一方，利用闲置电能创造价值的运营模式[4]。由于电能共享市场中的标的物是“电能的使用权”，使得电力用户能通过出让使用权成为市场中的供给侧[17]，这不仅打破了电源和负荷的物理约束，也打破了电力设备所有权、使用权与调度权的界限，扩大了产消者的策略空间，还原了电能的商品属性。

但另一方面，产消者并非无偿地共享自身多余的电能，而是希望能够从电能共享市场中获得收益，这意味着产消者在电能共享市场中并非简单的合作关系[18]，为此本文针对产消者间的相互作用关系以及电能共享市场的交易机制进行了研究。

1.1 基于边际价格驱动的电能共享模式

1.1.1 产消者剩余模型

产消者由于集成了大量的灵活资源而同时具有生产者与消费者双重身份，通常满足边际成本递增和边际效用递减规律[19]，为方便讨论，本文以一次函数为例设计了产消者的供求函数，如式(1)所示。

(1)

式中：PD,i和PS,i表示产消者i的边际效用和边际成本；Di和Si表示产消者i的电力需求与发电量；ai和bi表示产消者i的消费偏好，由产消者自身根据经验确定；αi和βi表示产消者i的生产系数，同样由产消者自身的经验确定。

并由式(2)计算产消者i的累计效用与累计成本。

(2)

式中：QD,i和QS,i表示产消者i的累计效用和累计成本。

此时产消者i的剩余能够由式(3)计算得到。

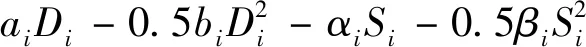
(3)

式中：Ui表示产消者i的剩余。

当产消者不参与电能共享市场时，其将以自发自用的方式运行[20]，对应的平衡条件为Di,*=Si,*，而产消者希望自身的剩余最大化。若不考虑稀缺性，产消者的运行方式如图2所示。

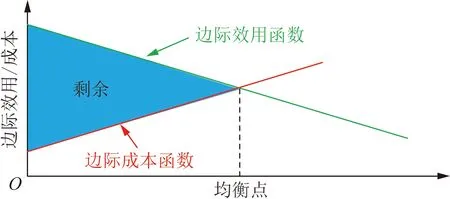
图2 产消者的自发自用状态Fig.2 Self-sufficiency of prosumer

由图2可知，产消者将根据ai-biDi=αi+βiSi决定其生产消费计划，此时其运行点能够由式(4)计算得到。

(4)

式中：Si,*和Di,*表示产消者i的生产消费计划。

1.1.2 边际价格与广义供求特性

在式(4)所示的运行点下，产消者的边际价格如式(5)所示，其边际效用等于边际成本，意味着额外的生产将不会带来剩余的提升。

λi=ai-biDi,*=αi+βiSi,*

(5)

式中：λi表示产消者i的边际价格。

一般情况下，有限的负荷水平与发电容量造成了电力资源的稀缺性，如式(6)所示。

(6)

式中：Di,max和Si,max表示产消者i的最大负荷与发电容量。

图3展示了稀缺性对电能共享的影响。

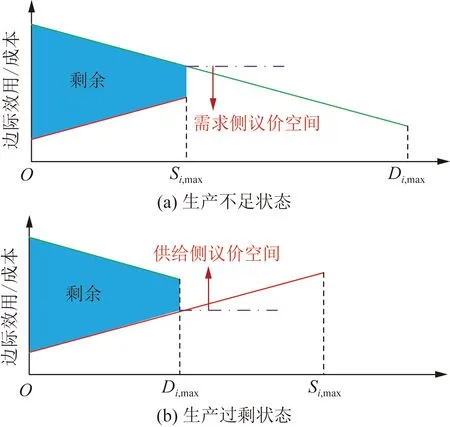
图3 稀缺性对电能共享的影响Fig.3 The impact of scarcity on power sharing

如图3所示，在生产不足状态下，产消者的运行方式由其发电容量决定，此时其运行点与边际价格由式(7)计算；在生产过剩状态下，产消者的运行方式由其最大负荷决定，此时其运行点与边际价格如式(8)计算。

(7)

(8)

显而易见，生产不足与生产过剩是一组相对状态。在图3中，生产不足的产消者有强烈的意愿购买额外的电能，成为了电能共享市场中的需求侧；生产过剩的产消者则作为供给侧，双方的议价空间由其边际价格决定。

同时，综合上述可知，当边际价格确定时，产消者的生产消费计划能够由式(9)计算得到。

(9)

若按照式(9)计算得到的发用电量超过最大值，则实际取最大值；若小于0，则实际取0。

1.1.3 电能共享市场出清机制

产消者通过报价参与电能共享市场，市场将根据所有产消者的报价进行排序，并决定产消者的身份与出清电量。根据市场规则，报价高的产消者作为需求侧，报价低的产消者作为供给侧，最终所有产消者按照统一的共享价格进行支付[21]。此时市场出清相当于求解式(10)所示的线性规划问题，其约束条件如式(11)和式(12)所示。

(10)

式中：πi表示产消者i在电能共享市场中的报价；Ei表示产消者i的共享电量，当其为正数时表示其从电能共享市场购买电能，当其为负数时表示其向电能共享市场出售电能；N表示产消者集合。

式(11)表示产消者的申报容量约束，式(12)表示电能共享市场的电量平衡约束。

-Si,max≤Ei≤Di,max,∀i∈N

(11)

(12)

电能共享市场出清问题的拉格朗日函数如式(13)所示，其Karush-Kuhn-Tucker(KKT)最优性条件如式(14)和式(15)所示。

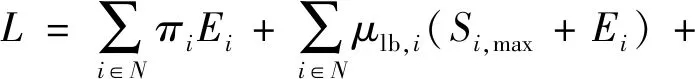
(13)

式中：μlb,i和μub,i是式(11)的对偶变量；λe是式(12)的对偶变量，即为电能共享市场出清电价。

πi+μlb,i-μub,i-λe=0,∀i∈N

(14)

(15)

式中：⊥为互补算子，a⊥b等价于ab=0[22]。

进一步定义消费者剩余和生产者剩余，如式(16)所示。

(16)

式中：UD,i和US,i表示产消者i的消费者剩余和生产者剩余。

当共享出清电价为λe时，产消者的生产消费计划如图4所示。

图4 产消者的电能共享状态Fig.4 The diagram of power sharing at demand side

在图4中，由于共享出清价格高于共享前产消者的边际价格，使得产消者成为了共享市场中的供给侧，向共享市场出售电能。参与共享交易后，产消者的消费者剩余有所下降，而生产者剩余显著提升，使得总剩余增加，这意味着产消者能够从共享市场中获得收益。值得注意的是，产消者不仅通过增加发电量成为共享市场中的供给侧，更是通过减小自身负荷进一步增加了共享电量。可见，电能共享打破了传统电源与负荷的界限，使得产消者能充分利用自身灵活性而在市场中表现出广义供求特性。

1.2 电能共享市场博弈均衡分析

1.2.1 产消者的最优反应函数

在上述共享模式下，产消者的平衡条件如式(17)所示，其对偶变量即为产消者的边际价格λi。

Di=Si+Ei

(17)

产消者通过报价参与电能共享市场，与其余产消者相互作用，其最优反应函数如式(18)所示。

(18)

在式(18)中，产消者i通过优化自身的报价，旨在最大化自身的剩余。然而产消者需要按照市场出清电价进行支付，而市场出清电价由所有产消者的策略共同决定，因此产消者之间构成了纳什博弈。同时，电能平衡约束的存在使得产消者之间的策略空间存在耦合，形成了广义纳什均衡[23]。

以产消者A和B构成的电能共享市场为例，其最优反应函数如式(19)和式(20)所示。

(19)

式中：DA和SA表示产消者A的电力需求与发电量；EA表示产消者A的共享电量；aA和bA表示产消者A的消费偏好；αA和βA表示产消者A的生产系数；λB表示产消者B的边际价格；DA,max和SA,max表示产消者A的最大负荷与发电容量。

(20)

式中：DB和SB表示产消者B的电力需求与发电量；EB表示产消者B的共享电量；aB和bB表示产消者B的消费偏好；αB和βB表示产消者B的生产系数；λA表示产消者A的边际价格；DB,max和SB,max表示产消者B的最大负荷与发电容量。

1.2.2 电能共享市场的无谓损失

然而，现实中受制于市场无序困境，由式(18)定义的最优反应难以实现市场均衡，往往造成了市场的无谓损失[24]。

同样以产消者A和B的共享为例，假设产消者A的边际效用函数为PD,A=1.1-0.001DA，最大负荷为500 kW·h，边际成本函数为PS,A=0.4+0.001 7SA，最大发电量为250 kW·h；产消者B的边际效用函数为PD,B=0.8-0.001 5DB，最大负荷为200 kW·h，边际成本函数为PS,B=0.35+0.000 5SB，最大发电量为450 kW·h。可见产消者A的发电容量不足而产消者B发电容量过剩，同时产消者A具有更高的边际效用，而产消者B具有更低的边际成本，因此产消者B有足够的意愿向产消者A出售电能，形成电能共享。在不同的共享电量下，分别由式(19)和式(20)计算得到产消者A和B的最优反应，如图5所示。

图5 产消者A和B的最优反应Fig.5 The optimal response of prosumers A and B

在图5中，电能共享前产消者A和B的剩余为O点，随着共享电量的增加，产消者A和B的剩余共同增加，直到最高点M，此后共享电量的增加将导致产消者剩余的递减。可见点M为产消者A和B的最优反应点。值得注意的是，产消者剩余的变化轨迹出现了交点N。

额外的，定义社会福利最大化问题，如式(21)所示。其意味着通过集中组织产消者的生产消费计划，从而实现电力资源的最优配置[25]。

(21)

图6展示了不同共享电量下电能共享市场的社会福利与产消者的边际价格。

在图6中，M点为产消者A和B的最优反应点，但却没有实现社会福利最大化，而在N点处电能共享市场的社会福利达到了峰值。

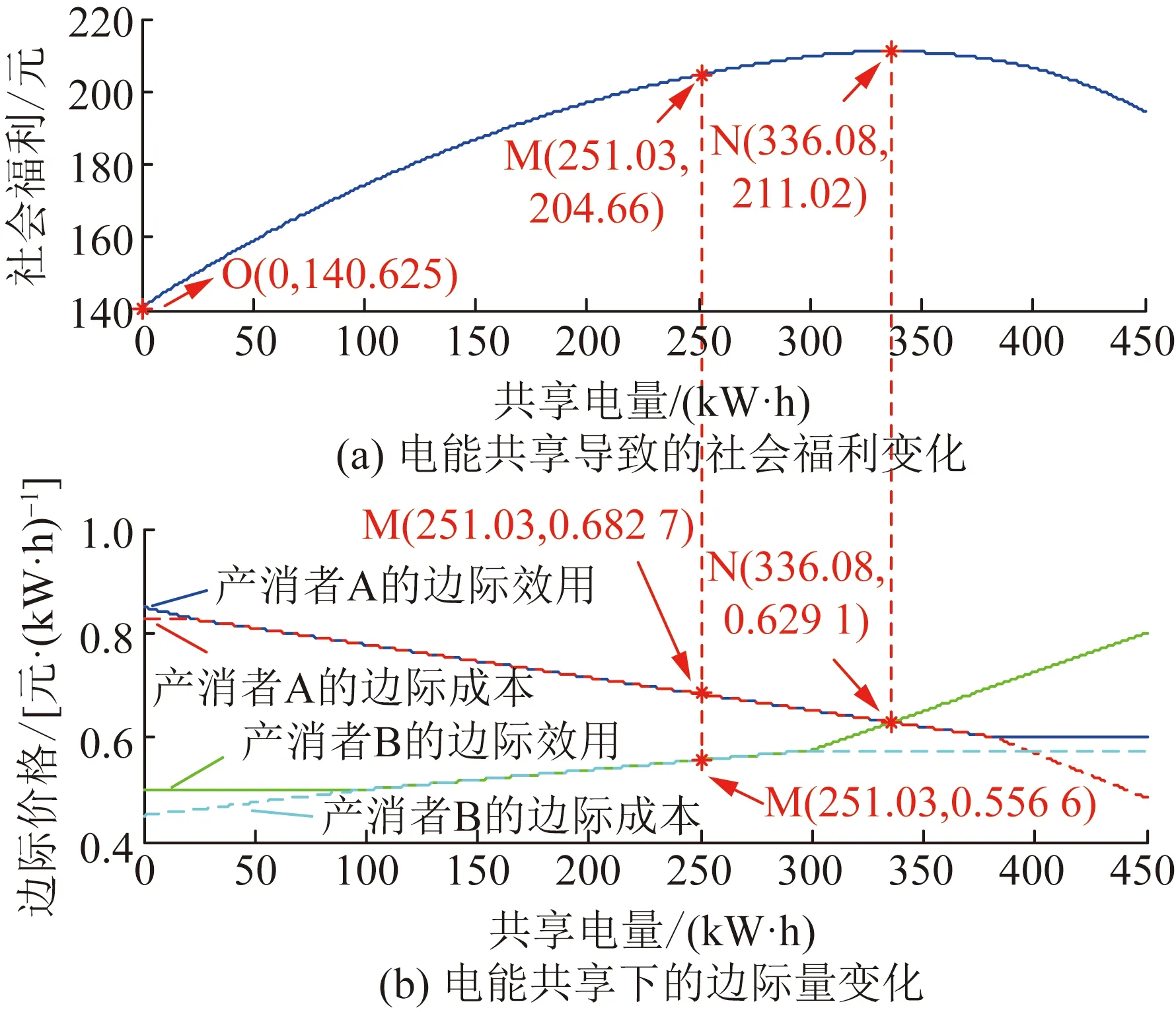
图6 电能共享市场福利变化Fig.6 The track of welfare in power sharing market

分析可知，产消者A在电能共享中扮演消费者，而产消者B扮演生产者。由式(19)和式(20)可知，为了追求市场权利，产消者A希望按照产消者B的边际成本购电，而产消者B希望按照产消者A的边际效用售电。在最优反应点产消者A的边际效用与产消者B的边际成本并不相等，这意味着双方没有实现价值的认同。在竞争性市场中，由于缺乏充分的沟通，产消者A和B在价格上没有达成一致，导致市场无序竞争，造成了电能共享市场的无谓损失，其与社会福利最优值的差异称为市场的无序代价。

2 基于价值认同的共享交易机制

由上述分析可知，传统基于个体最优反应函数的市场交易机制无法适应电能共享市场变幻莫测的供求关系。而进一步观察图6可知，在社会福利最大处，产消者A的边际价格与产消者B相等，这意味着双方实现了电能价值的认同。因此猜想：电能共享市场社会福利最大化的关键在于产消者间是否实现价值的认同。

式(21)的拉格朗日函数如式(22)所示，对Ei求导能够得到式(23)所示的最优性条件。

(22)

λ1=λ2=…=λi=…=λN-1=λN=λe

(23)

式(23)揭示了电能共享市场实现社会福利最大化的机理，即所有产消者的边际价格相等，并等同于共享电价。

当共享网络为联通图时[26]，产消者之间能基于一致性协议在有限迭代次数内完成价值的认同。由式(23)可知可以选取产消者的边际价格λi作为一致性变量，并通过式(24)迭代更新。

(24)

式中：λi,k表示迭代次数为k时产消者i的边际价格；wij为一致性系数，通过式(25)计算，所形成的是一个行求和为1的矩阵；ζ为步长；γi,k-1为梯度，由式(26)计算得到。

(25)

(26)

式中：νij为反馈项系数，通过式(27)计算；Ei,k表示迭代次数为k时产消者i的共享电量。

(27)

一致性算法收敛判据如式(28)所示[27]。

(28)

由上述可知，基于一致性协议的价值认同方法是一种完全分布式算法，其不依赖于电力交易中心，而是基于信息网络完成电能共享市场的分布式交易，其流程如下所示。

步骤1产消者向智能电表输入个人偏好信息，包括{ai,bi,αi,βi,Di,max,Si,max}。

步骤2产消者按照自发自用方式优化生产消费计划，并根据式(5)、式(7)和式(8)计算边际价格，作为初始边际价格λi,0，并告知相邻节点；同时令γi,0=0和Ei,0=0，初始化k=1。

步骤3产消者根据式(24)更新一致性变量λi,k，并告知相邻节点。

步骤4由式(9)可知，产消者能根据式(29)计算得到生产消费计划Di,k和Si,k，并根据式(30)结算得到共享电量Ei,k。

(29)

式中：Di,k和Si,k表示迭代次数为k时产消者i的电力需求与发电量。若按照式(29)计算得到的发用电量超过最大值，则实际取最大值；若小于0，则实际取0。

Ei,k=Di,k-Si,k

(30)

步骤5根据式(26)更新梯度为γi,k，并告知相邻节点。

步骤6根据式(28)判断是否收敛。若收敛，完成电能共享市场出清；若不收敛，令k=k+1并返回步骤3。

3 数值仿真分析

本文在10个产消者构成的电能共享网络中进行了仿真，仿真是在Intel(R) Core(TM) i5-6400 @2.70 GHz CPU，4 GB RAM硬件环境下，64位Windows 10操作系统中通过MATLAB R2014a编程完成的，仿真过程中ζ为10-4，ξ为10-8。

产消者之间的信息物理连接关系如图7所示。其偏好参数与自发自用下的生产消费计划如表1所示。

图7 10个产消者组成的电能共享网络Fig.7 Power sharing network including 10 prosumers

由表1可知，在自发自用状态下，产消者的边际价格各不相同。边际电价较高的产消者例如P3、P4和P9期望以更低的价格购买电量；而边际电价较低的产消者，例如P1、P6和P7期望以更高的价格出售电量，因此产生了足够的动力进行电能共享。然而由于交易机制的缺失，产消者被迫以自发自用的方式运行，其总发电量为2 988.43 kW·h，总发电成本为1 826.24元，总用电效用为2 799.68元，总的社会福利为973.44元。

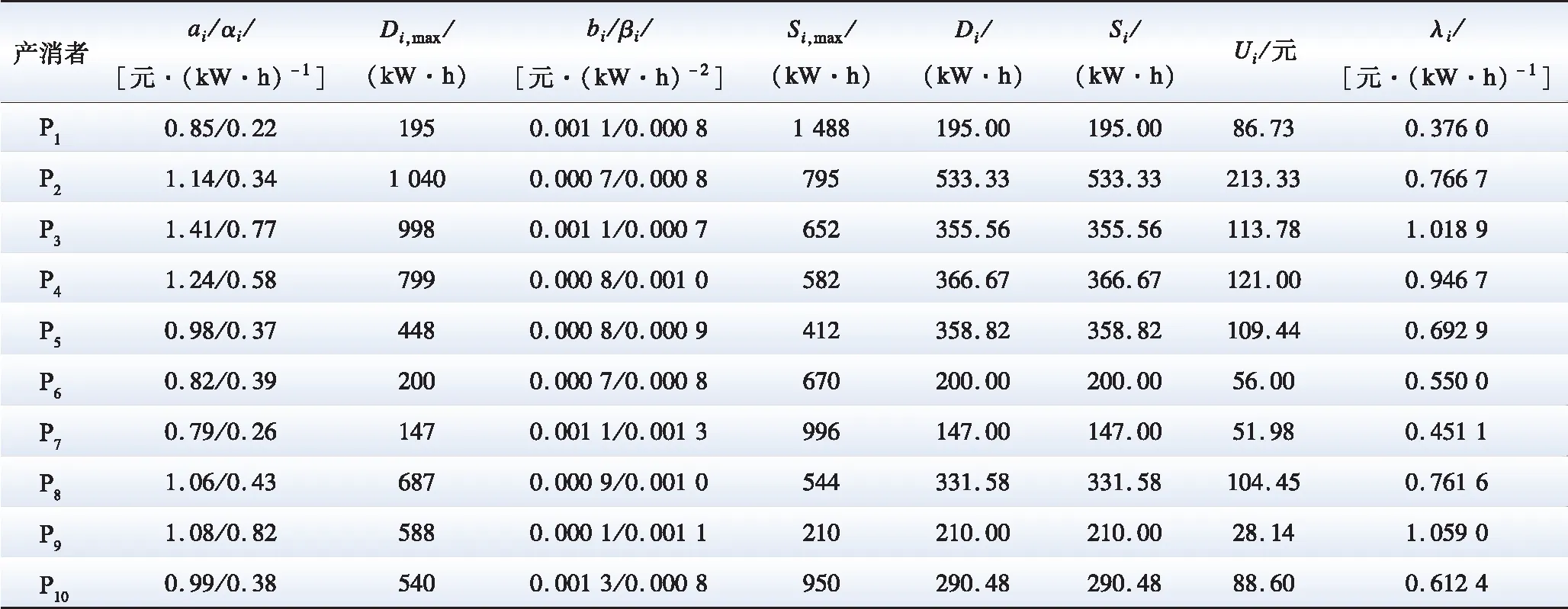
表1 产消者的偏好与自发自用状态Table 1 The preference of prosumers and the state of self-sufficient

在图7所示的共享网络下，产消者能够向相邻节点传递信息或接受来自相邻节点的信息，这意味着产消者之间能交换价格信号，从而实现价值的传递与共识。不同于现有的电力市场交易机制，本文所提出的共享交易机制不依赖于电力交易中心，而是能够自发地实现电能共享市场的出清。

在一致性协议下，每个产消者的边际价格λi在迭代中的更新过程如图8所示，对应的共享电量如图9所示。

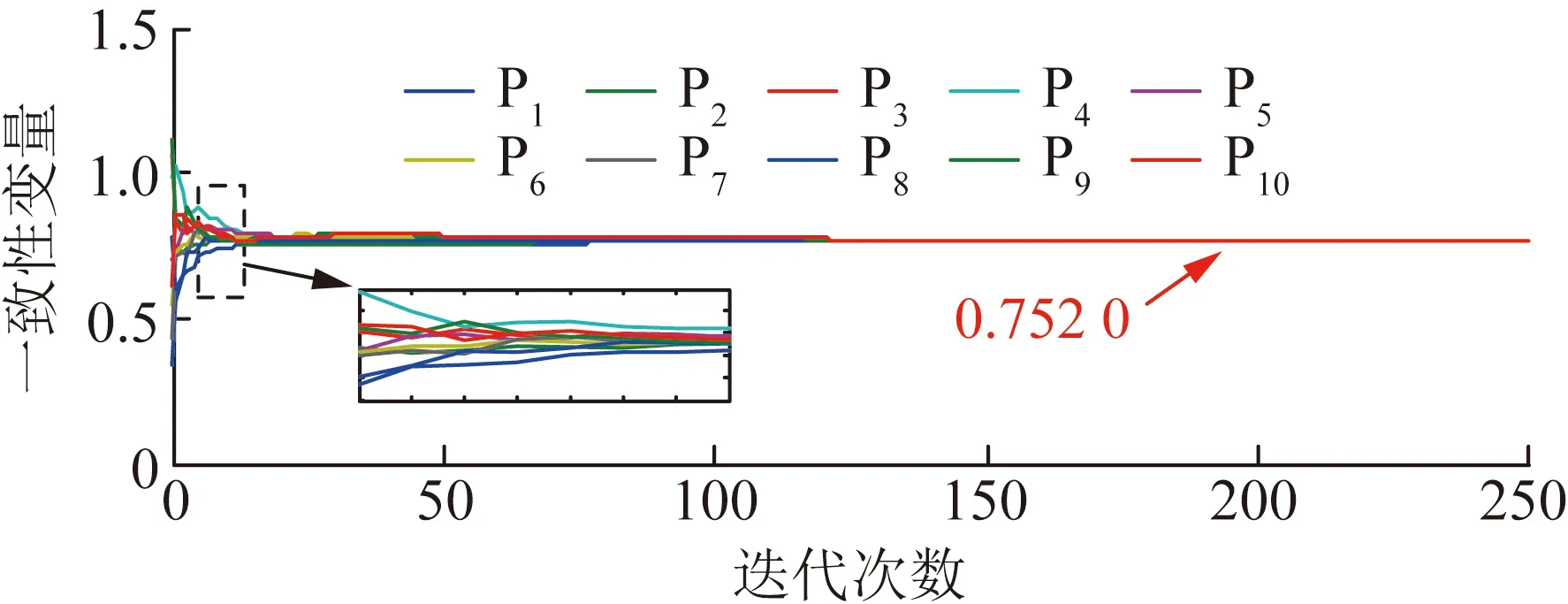
图8 一致性变量更新过程Fig.8 The iterative process of consistent

图9 共享电量更新过程Fig.9 The iterative process of power sharing

如图8和图9所示，经过有限迭代后，产消者的边际价格收敛于相同值，且该值即为电能共享市场的出清价格，同时共享电量趋近于稳定的数值，因此完成了电能共享市场的分布式出清。另一方面，由于本文所提的交易机制并不涉及复杂的数学计算，在本文所述仿真环境下仅用时0.025 s即完成电能共享市场的分布式出清。即使考虑通信延时的存在，依然能够胜任实时电能共享交易，因此未来能通过智能电表[28]实现，由于交易过程不依赖于电力交易中心，因此能够大大降低交易成本。另一方面，用户的效用偏好和生产系数等私人信息仅需存储于智能电表而不必上传至电力交易中心，且电能共享交易过程中仅传递共享电量，避免了信息的泄露，从而保护了产消者的隐私安全。

在一致性协议下，产消者的电能共享出清结果如表2所示。

表2 产消者的电能共享结果Table 2 The results of power sharing

由表2可知，产消者的总发电量上升为3 381.78 kW·h，总发电成本为1 850.99元，总用电效用为3 287.15 元，总福利上升为1 436.16元，提升了47.53%，共享电价为0.752 0元/(kW·h)。同时，表2中的共享电量与式(21)所示社会福利最大化问题具有相同的结果，这意味着在本文所提交易机制下，电能共享市场实现了社会福利最大化。

进一步对比表1与表2可知，电能共享后产消者的边际价格均等于出清价格，因此实现了关于电能价值的认同。同时，电能共享后产消者个体的剩余均得到了提升，可见本文所提共享策略是帕累托改进的，能够实现产消者的共赢，因此产消者将有足够的意愿参与电能共享市场。另外值得注意的是，电能共享市场的出清电价将高于共享前产消者的最低边际价格并低于最高边际价格。这是由于电能共享建立了产消者间的贸易关系，扩大了产消者的策略空间，使得产消者能够购买更为廉价的电能或以更高的价格出售电能。可见电能共享市场帕累托改进的本质是促进了电力资源的优化配置，使得低成本的电能尽可能流向高效用负荷，从而创造“经济蛋糕”。

4 结 论

针对需求侧电能共享市场的交易机制问题，本文剖析了现有基于产消者最优反应函数的交易机制无法实现电力资源优化配置的机理，从而提出了基于价值认同的分布式交易机制。在本文所提机制下，产消者之间通过一致性协议完成价值的传递与共识，从而避免了市场的无谓损失。仿真结果表明，在达成价值认同后，产消者的边际价格相等并等同于出清价格，避免了产消者之间的无序竞争，从而促进了电力资源的优化配置，实现了电能共享市场社会福利最大化。同时，在分布式交易机制下，电能共享市场能够自发出清而不再依赖于电力交易中心与复杂的投标流程，从而降低了交易成本。

在今后的研究中应当进一步计及电能传输过程中的“过网费”，并考虑线路阻塞对电能共享的影响。