A6061薄壁圆锥管轴向压缩性能的数值分析和理论研究

韦铁平 周兴洋 郭金泉 曾寿金 叶建华 杨晓翔

1.福建工程学院机械与汽车工程学院，福州,3501182.福建省力值计量测试重点实验室，福州，3500033.福州大学机械工程及自动化学院，福州，350116

0 引言

缓冲吸能元件通过塑性屈曲变形吸收冲击动能，在碰撞、爆炸等意外工况下起到保护主体构件的作用。其中，薄壁圆锥管因其低峰值载荷与良好的稳定性被广泛应用于汽车防撞领域。目前国内外对圆锥管的研究大多是在小范围锥倾角内，对大范围锥倾角的圆锥管吸能特性的研究还不够完善。

锥倾角使得薄壁管整体稳定性显著提高，但研究发现较大的锥倾角会导致结构比吸能降低。ALGHAMDI等[1]对锥倾角为15°～60°的圆锥管进行轴向压缩仿真，研究结果表明锥倾角大于40°时，圆锥管更易塌陷，吸能性差。ALJAWI等[2]对上述仿真结果进行了试验，发现试验结果与仿真分析是吻合的。

15°以内的锥倾角圆锥管的吸能特性已得到充分研究。MAMALIS等[3]通过对5°～10°锥倾角范围的圆锥管进行仿真分析，研究圆锥管轴向载荷下的吸能特性，发现圆锥管在压缩过程中存在两种变形模式：一种是整个压缩过程均为环形对称模式；另一种是在压缩初始阶段为环形对称模式，随着锥倾角和壁厚的改变，在某一时刻转变为钻石模式。冯悦等[4]通过仿真计算研究了锥倾角分别为1°、3°、5°和7°的圆锥管在不同冲击速度下的吸能特性。METE等[5]通过仿真计算分析了锥倾角分别为3°、7°、10°、12°和15°的圆锥管在轴向载荷作用下的吸能特性。张良[6]采用试验和仿真计算相结合的方式，分析锥倾角分别为2°、4°和6°的多边形多胞锥形管的耐撞性规律。

在圆锥管的理论研究方面，POSTLETHWAITE等[7]基于ALEXANDER[8]提出的理论对锥倾角为5°～20°的圆锥管在轴向压缩下展开研究，推导出锥形管平均载荷预测公式；MAMALIS等[9]研究了轴向压缩下锥倾角为0°～14.35°薄壁圆锥管的压溃现象，建立了平均载荷理论模型，发现理论模型与仿真、实验结果相一致；进一步地，MAMALIS等[10]对锥倾角为0°～14.35°的圆锥管建立了瞬时载荷理论模型，发现理论模型与试验结果吻合较好；洪武等[11]提出了锥倾角为30°～40°的圆锥管在“环形-嵌套”模式变形时吸能规律的预测方法。上述有关圆锥管的理论均是在圆直管的理论基础上推导出来的，且研究范围主要针对小范围锥倾角,并没有对大范围锥倾角的适用性进行探索。

本文在轴向载荷作用下对锥倾角为0°～40°、壁厚为1～2.5 mm的A6061圆锥管进行仿真计算，分析锥倾角和壁厚对薄壁圆锥管吸能特性和变形模式的影响规律，并研究现有瞬时载荷公式的适用性。在此基础上，采用皮尔逊修正系数分析法提出适用于大范围锥倾角(15°～40°)的瞬时载荷预测表达式，并通过试验进行验证。

1 评价指标

基于汽车前端吸能盒的设计，本文薄壁圆锥管的吸能特性指标设定为初始峰值载荷(initial peak load，IPL)FIPL、比吸能(specific energy absorption，SEA)ESEA、平均载荷(mean load，ML)FML[12]。

(1)初始峰值载荷FIPL。初始峰值载荷是压溃过程中出现第一个褶皱时所产生的碰撞力最大值，其值越大，碰撞减速度越大，对乘员造成的伤害越严重，因此，FIPL越小，耐撞性能越好。

(2)比吸能ESEA。比吸能为结构的单位质量所吸收的能量，它代表了结构发生碰撞时，其材料在能量吸收中的利用率,因此，ESEA越大，薄壁构件吸能能力越高。ESEA的定义为

(1)

式中，E(s)为压缩距离为s时构件吸收的冲击能；M为吸能构件的质量。

(3)平均载荷FML。平均载荷为压溃载荷在整个压缩过程中的平均力值，它表征了结构单位压缩量的平均吸能特性。一般情况下，FML值越大，耐撞性越好。FML的定义为

(2)

2 数值模拟

2.1 有限元模型

薄壁圆锥管的结构参数主要包括两个尺寸：壁厚和锥倾角。基于文献[11]的大范围圆锥管设计方案，本文选取了表1所示的结构尺寸。如图1所示，管高L和大端外径D固定；锥倾角φ从0°增大至40°，步长为5°；小端外径d随锥倾角φ的增大而相应增大；壁厚tw从1 mm增至2.5 mm，步长为0.5 mm。

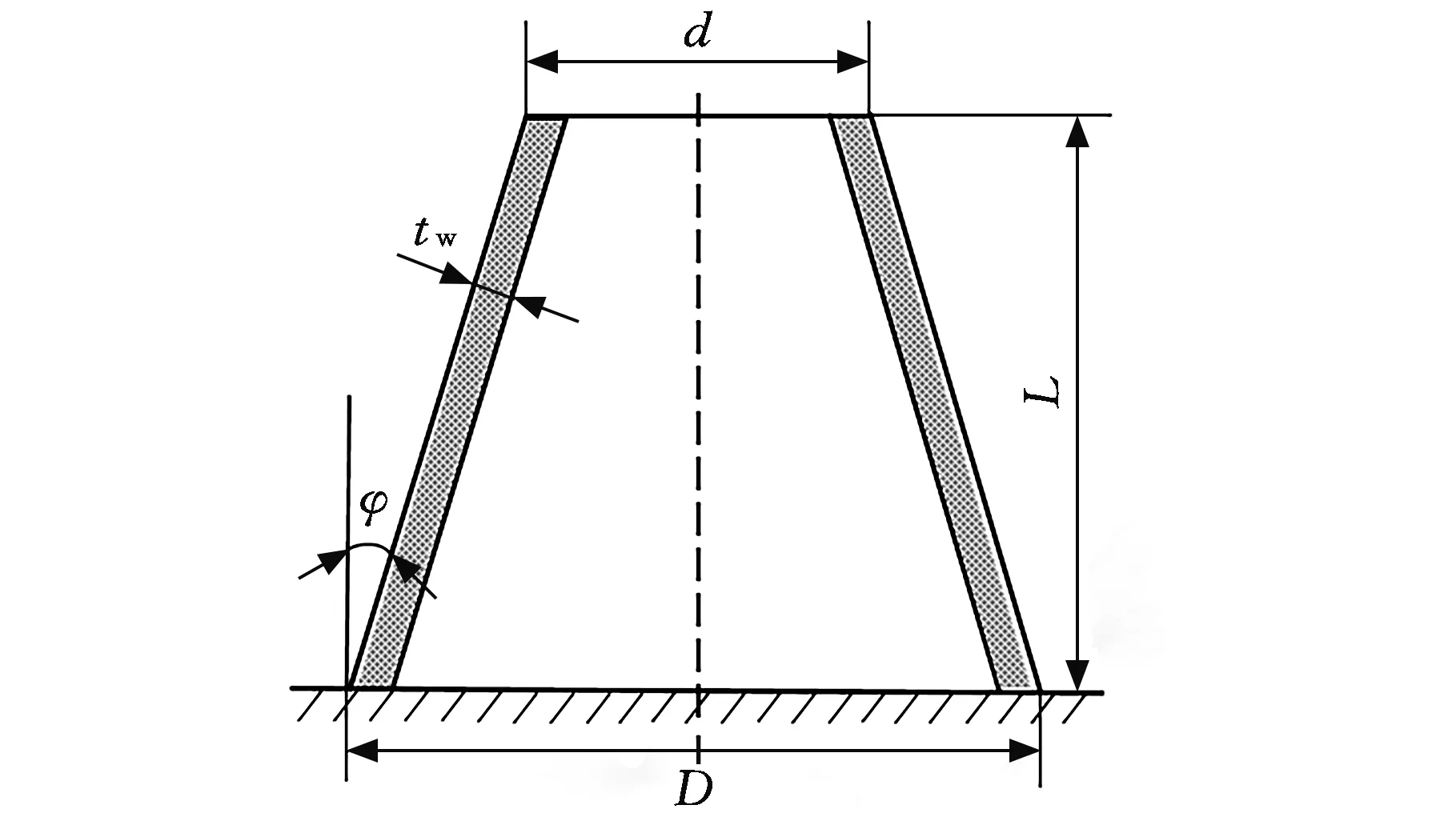
图1 模型尺寸示意图

表1 模型尺寸参数

如图2所示，按照GB/T 228-2010和GB/T 2975-1998的要求对试样铝合金A6061材料进行单轴拉伸试验，获得应力-应变关系曲线，如图3所示。由于A6061对应变率不敏感，故本研究不考虑应变率对材料参数的影响。A6061的材料性能参数见表2。

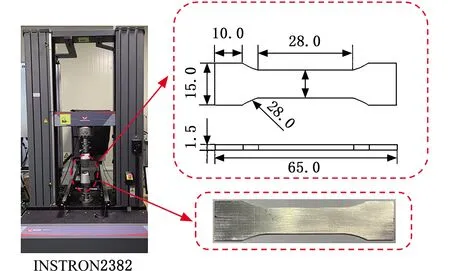
图2 A6061试样拉伸试验

图3 A6061材料应力-应变曲线

表2 A6061材料性能参数

采用有限元软件ANSYS/LS-DYNA模块进行数值计算。模型包含圆锥管、冲头及固定面板；薄壁管与冲头，以及固定面板间的静摩擦因数、动摩擦因数均设为0.2；三个部件间的接触方式设为“自动单面接触”。

在压缩过程中固定面板不动，冲头以1 m/s恒速向下压缩,如图4所示。在实际情况中，由于冲头和固定面板相对于薄壁管件而言，其抗变形刚度要大很多，因此，模型中的冲头和固定面板均设为刚性板，选用刚性材料Mate20#来模拟。此外，薄壁圆锥管壁厚小，采用Belytschko-Tsay壳单元，选用Mate24#来模拟。

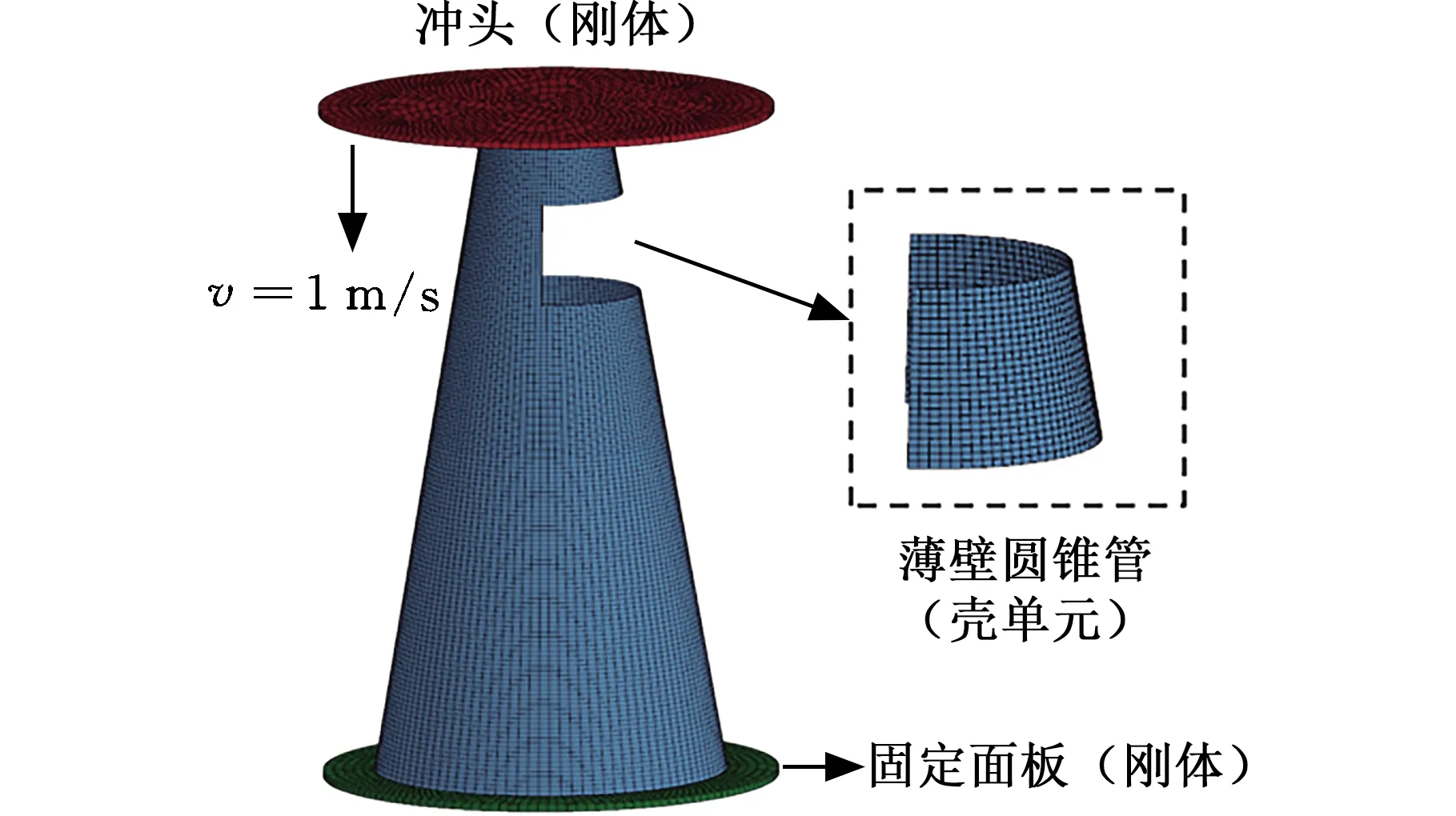
图4 有限元模型示意图

2.2 有限元模型验证

为了验证有限元模型的准确性和可靠性，本文进行了与文献[3]一致的有限元模型分析，将仿真结果的载荷-位移曲线与变形模式进行对比，发现本文结果与文献[3]结果十分吻合(图5、图6)，从而证明了本文仿真模型准确、可靠。

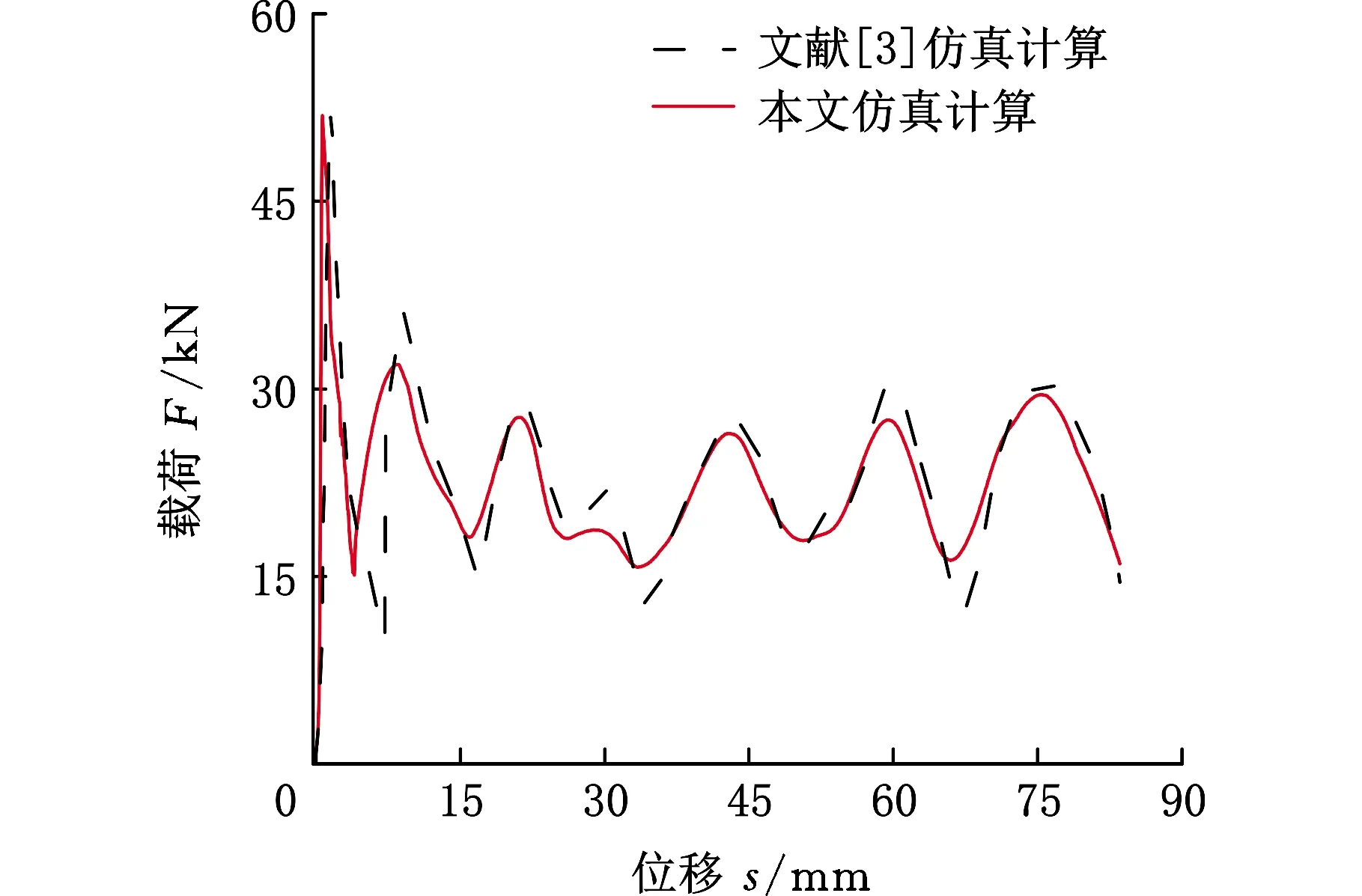
图5 本文仿真计算与文献[3]的载荷-位移曲线对比图

(a)文献[3]试验的变形模式

2.3 网格尺寸的影响

网格尺寸对仿真结果和计算成本有重要影响。本文对锥倾角为5°的薄壁圆锥管1.0～3.0 mm的不同单元尺寸模型进行了模拟计算。如图7所示，不同单元尺寸下，圆锥管小端端口处的应力-时间曲线在弹性阶段(初始波峰)的趋势一致，但在渐进屈曲阶段有较大的差异，原因是粗网格不能正确地表示折叠现象[12]，且粗网格模型的变形模式会出现畸变，更快达到压实期，因此，粗网格不适用于仿真计算。由图7可知，当网格尺寸小于2.0 mm时，应力-时间曲线显得更加平坦(波峰数少)，即计算结果更加贴近实际压溃模式。单元尺寸为1.5 mm时具有最佳计算效率且满足计算精度要求。

图7 网格灵敏度分析结果

3 仿真结果与分析

3.1 准静态轴压下圆锥管的屈曲行为

图8为φ=10°、tw=2 mm圆锥管的载荷-位移曲线。在压溃初期，圆锥管的压溃载荷急剧增大到最大值(A点)，此时圆锥管处于弹性阶段；随着外力的持续作用，圆锥管由弹性阶段过渡到塑性阶段，压溃载荷迅速降低；之后，压溃载荷在小范围内呈现有规律的波动起伏(CF段)，直到结构被压至密实化阶段(F点之后)，压溃载荷迅速增大到极大值点。

图8 φ=10°、tw=2 mm模型的载荷-位移曲线

其中，稳定渐进屈曲阶段即为稳定的应力平台区；每次波动代表一次局部折叠过程，如BD段与DF段，分别为压缩过程中形成的褶皱，绝大部分有效的能量耗散均在此阶段完成。

3.2 锥倾角与壁厚对薄壁圆锥管吸能特性的影响

3.2.1初始峰值载荷

几何参数对圆锥管吸能特性的影响规律如图9所示。由图9a可知，不同壁厚下的初始峰值载荷均随着圆锥管锥倾角的增大而减小，且壁厚越大，初始峰值载荷也越大。这是由于随着锥倾角的增大，初始压缩截面积减小，结构刚度减小，使得初始峰值载荷减小。壁厚的增大导致初始压缩截面积增大，则结构刚度增大，进而导致峰值载荷增大。

3.2.2平均载荷

由图9b可知，圆锥管锥倾角小于15°时，不同壁厚下圆锥管的平均载荷基本不变或略微减小；在15°～30°时，减小幅度较大；在30°～40°时，平均载荷趋于平稳。这是因为：

(1)锥倾角小于15°时，圆锥管变形模式为堆叠模式(与圆直管相似)，对圆锥管整体吸能效率影响小。

(2)锥倾角15°～30°时，变形模式由堆叠模式转变为嵌套模式，导致吸能效率降低。

(3)锥倾角大于30°时，以φ=35°、tw=2.5 mm的圆锥管为例展开研究，其载荷-位移曲线见图10。在压缩距离111 mm时，图10中1、2处(褶皱处)会触及底部面板(即直接受到底部面板的反作用力)，从而使得载荷骤增。该现象产生的原因是本文选用A6061材料的屈服强度低，在锥倾角大于30°时，圆锥管更易出现整体塌陷的压溃现象。

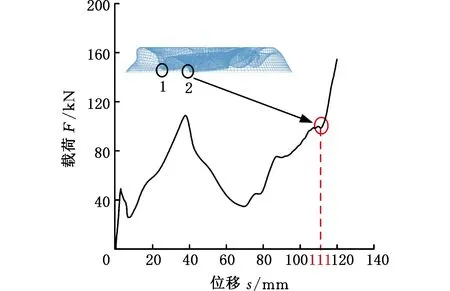
图10 φ=35°、tw=2.5 mm模型的载荷-位移曲线

3.2.3比吸能

如图9c所示，不同壁厚下的圆锥管比吸能在锥倾角0°～40°范围内均呈减小趋势，且壁厚越大，比吸能也越大。这是由于随着锥倾角的增大，用于吸收能量的压缩截面积减小，导致圆锥管比吸能减小。而壁厚的增大使得压缩截面积增大，用于塑性变形的吸能材料增多，从而使得比吸能增大。

(a)初始峰值载荷

3.3 锥倾角和壁厚对薄壁圆锥管变形模式的影响

φ=0°～40°、tw=2 mm的圆锥管的变形模式如图11所示。锥倾角15°为变形模式的临界角。当锥倾角小于15°时，变形模式为堆叠模式，吸能效率高；当锥倾角大于15°之后，变形模式由堆叠模式转为嵌套模式，易发生塌陷现象，从而导致吸能效率降低。

(a)堆叠模式

φ=5°、tw=1～2.5 mm的圆锥管的变形模式如图12所示。壁厚的增大使得轴向压缩下的圆锥管压溃变形更为规整，由钻石模式转为环形对称模式。

(a)钻石模式 (b)环形对称模式

4 理论分析

根据本文仿真分析结果，探讨Mamalis公式在锥倾角范围15°～40°的适用性，并采用皮尔逊相关系数分析法提出修正表达式。

4.1 Mamalis瞬时载荷公式[10]的适用性

目前用于分析圆锥管轴向压缩下吸能特性的理论研究情况如表3所示。由表3可知，相关研究在适用性上存在一定的局限性。本文依据Mamalis瞬时载荷公式[10]计算薄壁圆锥管轴向压缩的瞬时载荷，并展开分析。

表3 薄壁圆锥管现有理论研究

圆锥管的理论公式是基于圆直管理论模型，并结合圆锥管压缩时的几何关系(图13)推导而来。MAMALIS等[10]的瞬时载荷公式如下：

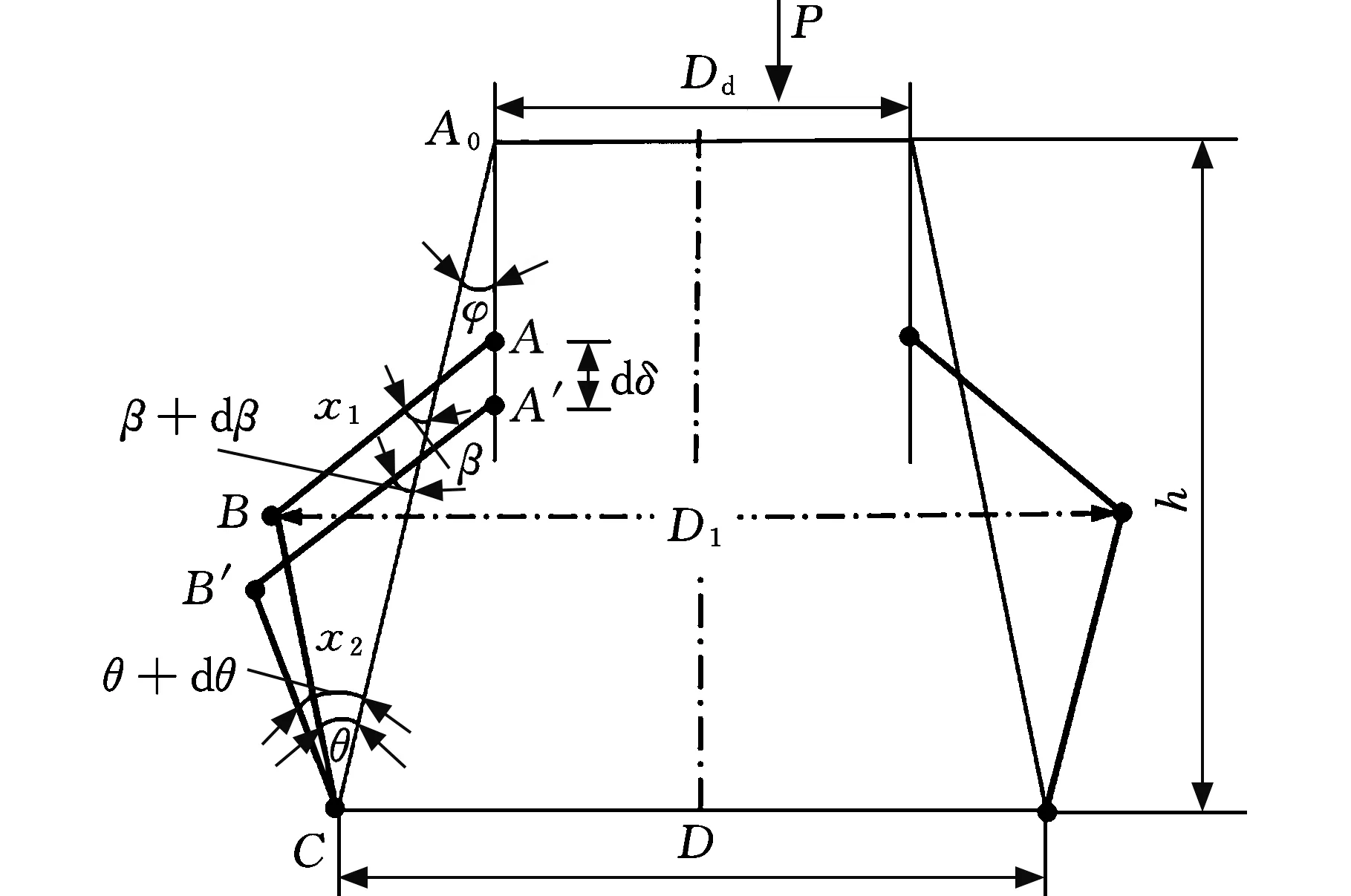
P：施加的轴向载荷 φ：圆锥管锥倾角 d：圆锥管小端直径 dδ：轴向压缩距离 D：圆锥管大端直径 θ：铰链BC与圆锥管壁的夹角 β：铰链AB与圆锥管壁的夹角 x1：铰链AB的长度 h：单个褶皱的垂直高度 x2：铰链BC的长度

(3)

其中

(4)

(5)

(6)

ψ′(θ)=θ-φ

(7)

(8)

(9)

由式(3)、式(7)和式(8)可知，存在唯一变量θ,因此，本文取θ=10°对圆锥管进行分析，如图14所示。

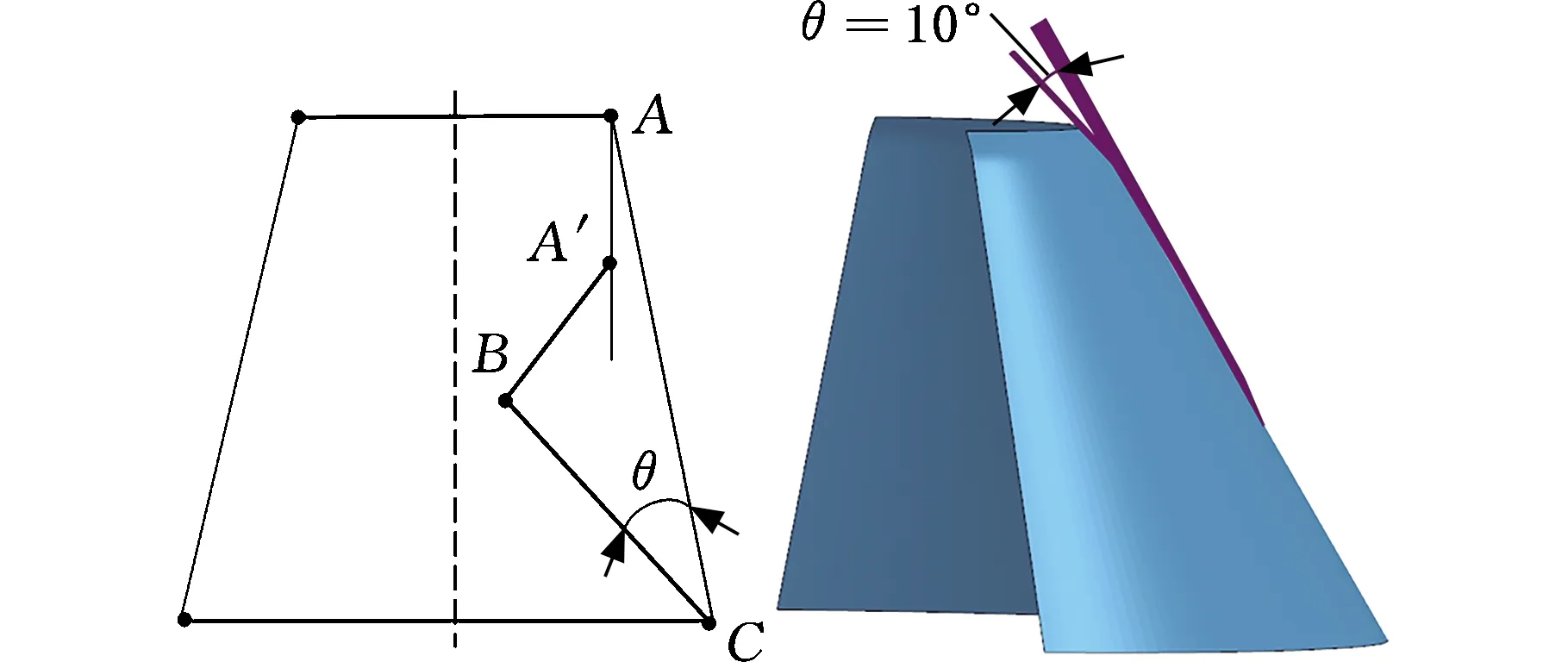
图14 φ=30°、tw=2 mm圆锥管叠缩示意图

图15为φ=30°、tw=2 mm圆锥管有限元计算的载荷-位移曲线图。图15显示，圆锥管在将要形成第一个褶皱时(θ=10°，以下计算相同)的载荷为43.09 kN，远小于理论计算结果150.87 kN。

图15 φ=30°、tw=2 mm圆锥管的载荷-位移曲线

表4和表5分别为φ=15°、θ=10°、tw=2 mm和φ=30°、θ=10°、tw=2 mm模型第一个褶皱形成时载荷仿真值与理论值的对比数据。由表4、表5可知，在锥倾角为15°时理论值与仿真值误差(以理论值为基准)在10%以内，而锥倾角为30°时误差骤增至50%以上。

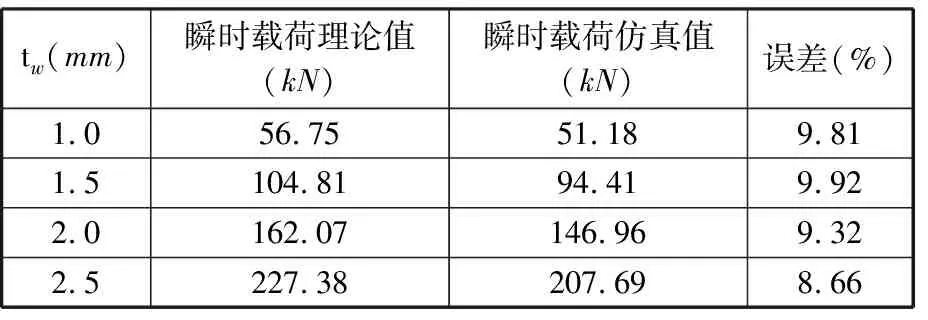
表4 φ=15°、θ=10°时瞬时载荷理论值与仿真值对比

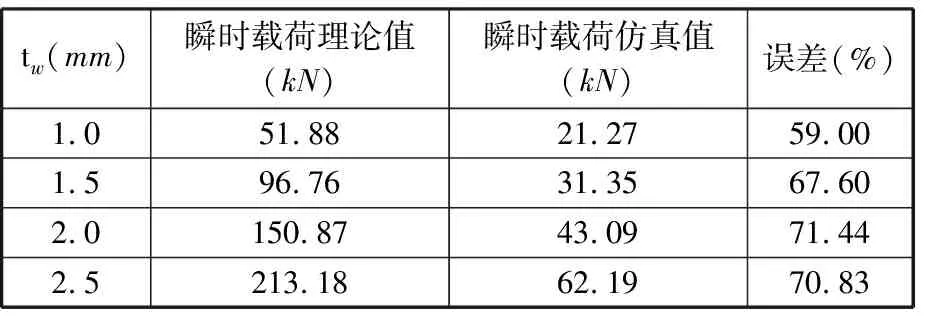
表5 φ=30°、θ=10°时瞬时载荷理论值与仿真值对比

通过仿真值与理论值的对比，验证了Mamalis瞬时载荷公式不适用于大锥倾角(>15°)的圆锥管,因此，本文将对Mamalis小倾角范围的瞬时载荷表达式进行修正，使其适用于15°～40°的大倾角圆锥管压溃机理。

4.2 大范围锥倾角(15°～40°)瞬时载荷修正模型

为使经典理论公式适用于大范围锥倾角，本文提出一种适用于薄壁圆锥管瞬时载荷理论模型的修正方法。考虑到理论公式与仿真模型的几何关联性，在已有圆锥管理论模型基础上，通过增设修正函数，采用皮尔逊相关系数分析法，获得瞬时载荷修正公式，使得理论值逼近仿真值，误差控制在10%以内。

4.2.1建立修正函数模型

在分析过程中，基于15°～40°锥倾角的圆锥管仿真结果和Mamalis瞬时载荷公式，增设包含主要敏感参数壁厚tw和锥倾角φ的修正函数，建立瞬时载荷修正公式：

Pf=f(φ,tw)P

(10)

其中，f(φ,tw)为增设的修正函数。

图16为φ=20°、tw=1.5 mm圆锥管有限元计算的载荷-位移曲线图。图16显示，曲线的初始阶段为直线段(Ⅰ处)，之后为一段弯曲段(Ⅱ处)。在直线段(Ⅰ处)增设一次项，在弯曲段(Ⅱ处)增设二次项。得到以下修正函数：

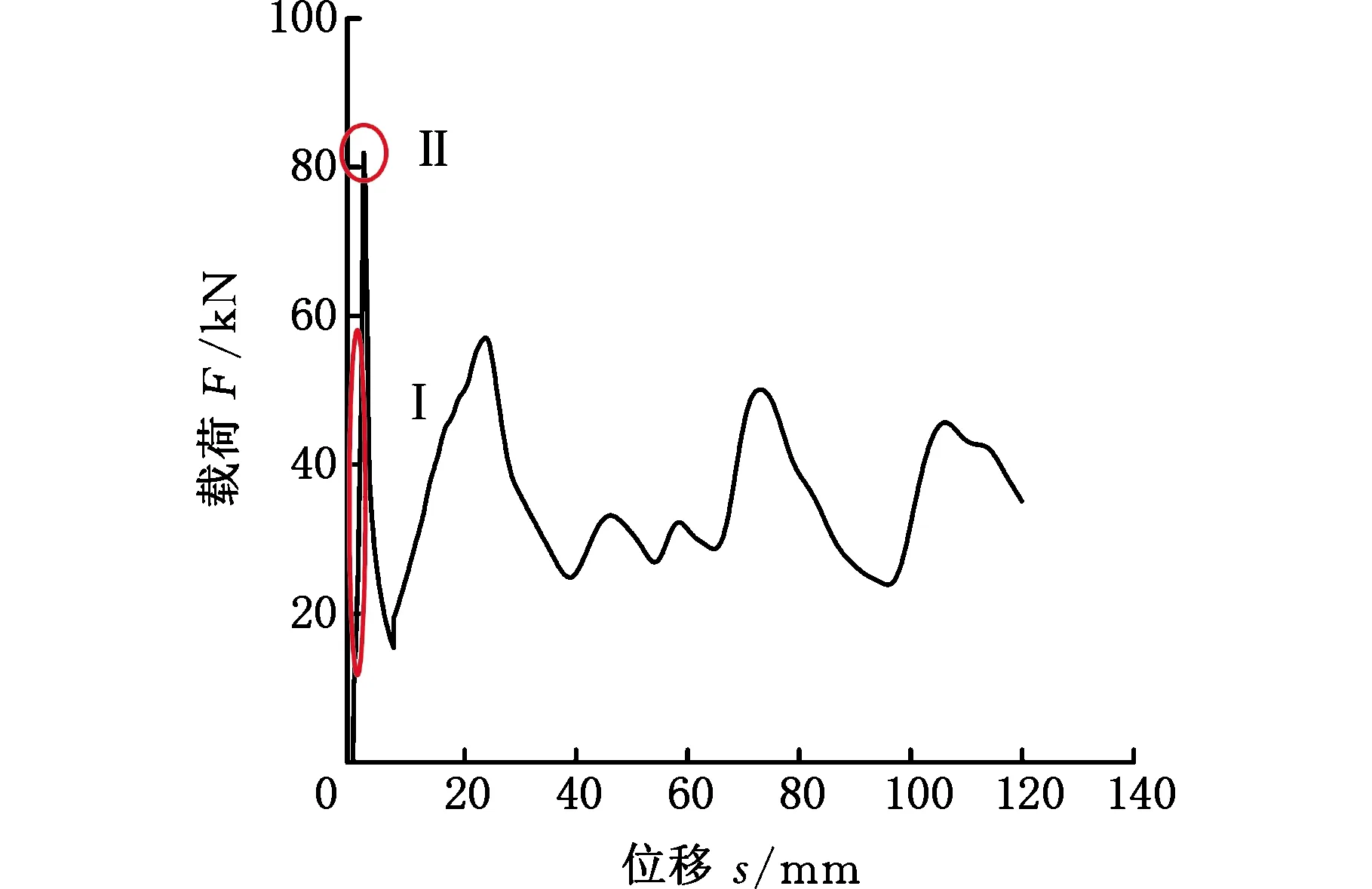
图16 φ=20°、tw=1.5 mm圆锥管的载荷-位移曲线

(11)

式中，a、b、c、e、g、h为待定参数。

4.2.2模型相关系数分析

采用皮尔逊相关系数分析法对拟定的修正函数进行相关性分析。皮尔逊相关系数的指标通常用r表示，取值范围为[-1,1]，表达式为

(12)

表6 r的取值范围与相关性的关系

表7 相关系数取值

f(φ,tw)=a+bφ+cφ2+etw

(13)

根据以下步骤对式(12)中a、b、c和e进行规划性求解：

(1)计算15°～40°锥倾角圆锥管的理论值和仿真值。

(2)确定修正函数模型f(φ,tw)。

实际做法：划分为男生、女生各四个组，其中每四组两个小组相对2～3 m之间进行站立，开展传接球的竞赛，同时也可以选择男女生之间进行分组竞赛。

(3)设定目标值(仿真值与修正理论值f(φ,tw)P的绝对值差值)最小。因为式(13)中有4个未知参数a、b、c、e，每次规划性求解可得一个值，多次计算确定最大值与最小值。

(4)对得到的极值进行加权平均计算，得到最终值，见表8。

表8 参数取值

得到修正函数：

f(φ,tw)=2.632 373 695-0.119 927 229φ+

0.001 653 464φ2-0.100 338 830tw

(14)

得到瞬时载荷修正表达式如下：

Pf=[2.632 373 695-0.119 927 229φ+

0.001 653 464φ2-0.100 338 830tw]P

(15)

表9 为修正结果值与仿真值的对比,可以看出，修正后的模型计算值(选取θ=10°)与仿真值之间最大误差为9.91%。

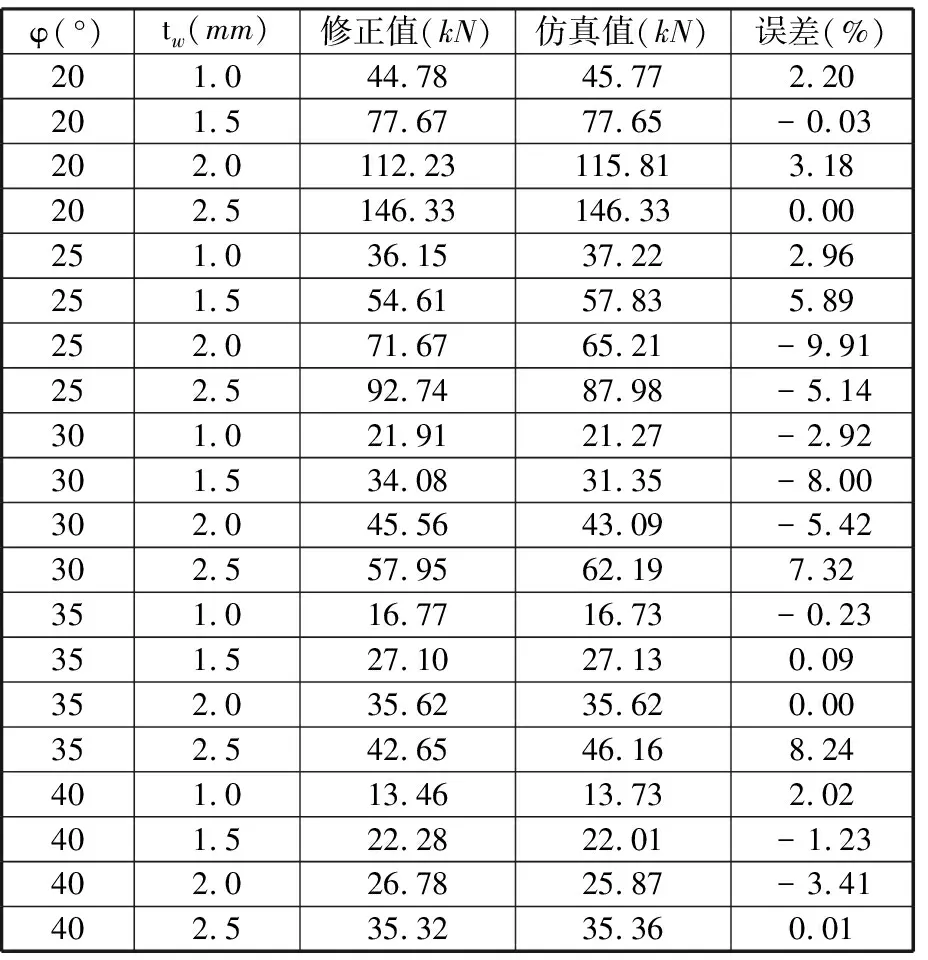
表9 瞬时载荷仿真值与修正值对比

综上所述，本文提出的瞬时载荷修正公式在15°～40°范围内具有良好的修正精度。

4.3 试验验证

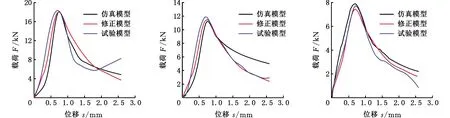
为了验证修正理论公式的准确性，基于相似律理论，按原模型尺寸1∶3进行缩放，通过DNS300电子万能材料试验机对缩放模型(φ=15°～40°、tw=0.87 mm)进行准静态压缩试验，将采集的试验值与缩放修正值和缩放仿真值进行对比，结果如图17所示。由图17可知，试验模型得到的载荷-位移曲线与缩放修正理论模型和缩放仿真模型的曲线均能较好地吻合。图18为试验模型和缩放仿真模型变形模式对比图，可以看出两者的变形模式吻合程度高。表10所示为试验值与缩放修正值和缩放仿真值的对比，可以看出，试验值与缩放修正值(选取θ=10°)之间最大误差为6.12%，与缩放仿真值(选取θ=10°)之间最大误差为5.90%。

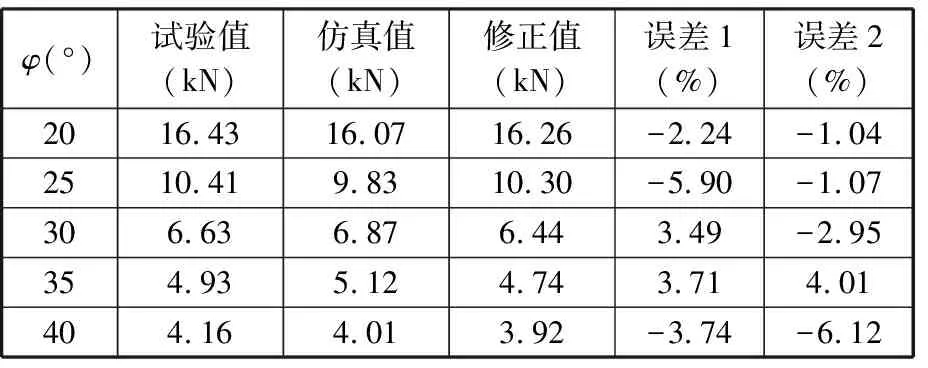
表10 试验值与缩放仿真值、缩放修正值对比

(a)φ=20° (b)φ=25° (c)φ=30°

图18 试验模型和缩放仿真模型变形模式

综上可知，试验结果验证了本文提出的修正理论模型的准确性，该修正理论模型能较好地对圆锥管的瞬时载荷进行预测。

4.4 0°～40°瞬时载荷表达式

MAMALIS等[10]基于锥倾角0°～14.35°圆锥管静态轴压试验，通过研究发现理论值与实验值较吻合；基于本文锥倾角0°～15°圆锥管静态轴向压缩的仿真结果与式(3)计算所得结果对比，发现最大误差在10%左右。

基于文献[10]的瞬时载荷表达式，结合本文锥倾角0°～15°圆锥管静态轴向压缩的仿真结果，提出了瞬时载荷修正表达式，修正值与仿真值对比，最大误差为9.91%，低于10%，如式(15)所示。

综上所述，锥倾角在0°～40°的瞬时载荷表达式如下：

(16)

5 结论

(1)锥倾角15°为变形模式的临界角，当锥倾角小于15°时结构的变形模式为堆叠模式，吸能效率高；大于15°时结构的变形模式复杂，由堆叠模式转为嵌套模式，更易发生塌陷现象，从而导致吸能效率低；而当锥倾角相同时，随着壁厚的增加，圆锥管的结构变形由不规整的钻石模式转为环形模式。

(2)随着锥倾角的增大，初始压缩截面积减小，结构刚度减小，使得初始峰值载荷变小；随着锥倾角的增大，用于吸收能量的压缩截面积减小，导致圆锥管比吸能减小。平均载荷在锥倾角小于15°时，由于变形模式为堆叠模式，与圆直管相似，故吸能效率基本不变；15°～30°时为嵌套模式，吸能效率低，导致平均载荷呈线性减小；锥倾角大于30°时，由于圆锥管易出现整体塌陷的压溃现象，使得平均载荷趋于平缓；而随着壁厚的增大，用于吸能的压缩截面积增大，结构刚度增大，导致圆锥管的初始峰值载荷、比吸能和平均载荷均显著增加。

(3)基于Mamalis瞬时载荷公式，提出了适用于锥倾角15°～40°圆锥管的瞬时载荷修正公式，修正结果与仿真模拟结果吻合良好，最大误差为9.91%。

(4)通过试验验证了修正理论模型的准确性，试验结果与修正结果和仿真模拟结果吻合良好，最大误差为6.12%。