计及横向剪切效应的环形谐振子理论研究

裴永乐，高立民，徐 亮，李 华，李晓辉，李录贤

(1.中国科学院西安光学精密机械研究所，西安 710119；2.西安交通大学航天航空学院，机械结构强度与振动国家重点实验室,飞行器环境与控制陕西省重点实验室，西安 710049)

0 引言

环形谐振子是谐振陀螺的一种典型谐振子结构类型，由于环形谐振子与旋转薄壳型谐振子(如半球谐振子)具有相似的动力学特性，因此可用环形谐振子的模型来简化研究半球谐振子唇缘的动态特性。经典的环形谐振子理论是在不考虑横向剪切变形的条件下，基于弹性力学基本原理以及几何中心线(或称几何中性轴)不可拉伸假设建立的，因此，该经典理论只适用于高径比(即结构高度与几何中心线曲率半径之比)较小的薄环结构。

在实践过程中，特别是在高过载条件下，如导弹的发射过程、弹体的侵彻过程等工况下，过小的高径比容易造成谐振子局部刚度不足，进而引起谐振子结构失效，因此，需要使用高径比较大的谐振子。在这种情况下，若仍使用忽略横向剪切效应的经典环形谐振子理论来设计谐振子，可能会造成很多问题，例如计算的弯曲挠度偏小、临界屈曲载荷偏大等。因此，目前亟需建立考虑横向剪切效应的环形谐振子理论及动态响应问题的求解方法，这对于高精度谐振陀螺的研究具有重要的工程意义和学术价值。

本文主要根据梁板理论的研究方法，从能量原理角度分析环结构的动态问题。基于横向剪切效应的梁板理论主要包括基于线性位移模式的低阶理论(如Timoshenko理论)和基于高次位移模式的高阶理论等。考虑到基于高次位移模式的高阶理论边界条件复杂、物理意义不明确，很难获得理论解。因此，为了便于工程计算，本文拟从经典Timoshenko理论的位移模式出发，根据经典环形谐振子理论的基本假设和能量原理，建立考虑横向剪切效应的环形谐振子新理论，并研究环形谐振子在缓慢、匀速转动过程中的动态响应问题。

1 环形谐振子结构的数学描述

(1)

图1 圆环结构及坐标系示意图Fig.1 The ring-shaped structure and its coordinate system

并且

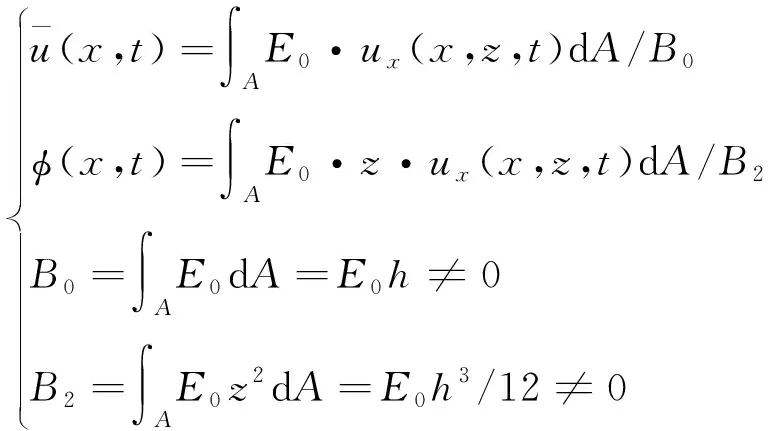
(2)

环形结构的几何关系可以表示为

(3)

其中，和分别为截面上的正应变和剪应变。

对于均质材料的环结构，其本构关系可以表示为

(4)

其中，和分别为截面上的正应力和剪应力；=[2(1+)]表示材料的剪切模量。

对于环结构问题，其广义应力的定义如下

(5)

其中，、和分别为周向拉力、弯矩和剪力。

因此，根据几何关系式(3)和本构关系式(4)，可得环结构的广义本构关系为

(6)

(7)

并且,“′”表示物理量对周向坐标的一阶偏导数。

2 环形谐振子结构的数学描述

对于一个缓慢、匀速转动的环形谐振子，其动态响应问题的求解一直是谐振陀螺领域的重要研究内容，特别是进动系数、二阶弯曲角频率等参数。因此，本节利用上述位移模式式(1)、广义应力式(5)、应变式(7)以及本构关系式(6)，根据哈密顿原理，对环形谐振子动态响应问题进行系统地研究和求解。

根据环结构的哈密顿原理，可得

(8)

并且

(9)

(10)

其中

(11)

将本构关系式(6)代入平衡方程式(10)中，从而有

(12)

至此，建立了考虑横向剪切效应的环结构理论，此外，环形结构的连续性(周期性)条件可表述为

(13)

3 动态问题的求解方法

进动系数及二阶弯曲角频率是谐振陀螺设计领域的重要参数，为了获得环形结构动态响应问题的理论解，同样引入几何中心线不可拉伸假设，从而有

(14)

即

(15)

(16)

其中，()和()为位移分布函数。

根据式(6)、式(7)和式(16)，对于动态问题，剪力(,)可表示为

(17)

为了评估横向剪切变形对结构动态响应的影响，考虑到式(16)，假设

()sin(2)]

(18)

其中，为待定系数，表征截面剪力大小，其值与、等物理量有关(见第4节)。

将式(14)和式(16)代入平衡方程式(12)，利用布勃诺夫-伽辽金法整理可得

(19)

其中

(20)

进而，进动系数和二阶角频率为

(21)

根据式(21)，基于本文理论获得环形谐振子的进动系数不再恒为2/5，其值会随着高径比等物理量的变化而改变；另一方面，由于待定常数的存在，利用经典的几何中心线不可拉伸假设及布勃诺夫-伽辽金法求解谐振子动态响应问题时，存在一个待定常数难以直接确定的问题。

4 待定常数的求解

为了确定待定常数，考虑到进动系数和二阶角频率的解析表达式中有相同的待求参数，并且很难通过其他方法获得进动系数的准确值。因此，本文拟利用二阶弯曲角频率值推导值，最终获得进动系数的精确值。对于环结构，在考虑横向剪切效应的条件下，获得环结构二阶弯曲角频率的最有效方法是有限元分析法。

在实践过程中，为了提高谐振子的品质因数，环形谐振子一般选取熔融石英材料，力学性能如下：密度=2201kg/m，弹性模量=727GPa及泊松比=016。此外，为了便于求解，这里取无量纲参数=，式(21)可转化为

(22)

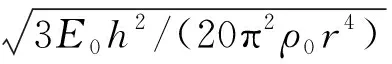
(a)有限元模型

(b) 二阶弯曲振型

图3 环结构二阶无量纲弯曲角频率ω2随h/r变化的规律Fig.3 The variation of the second-order dimensionless bending angular frequency for the ring structure with h/r increasing

同时，根据图3以及式(22)之二式，可获得曲率半径=20mm，50mm及100mm条件下值随的变化规律，如图4所示。根据图4可知，在不同的曲率半径条件下，参数随着的增加而单调增大：在较小时(如=002时)，趋近于零；在较大时(如=02时)，可达0.082左右。并且当曲率半径取不同值时，随着的增加，随着变化曲线的一致性很好，最大相对误差小于0.02%。

图4 参数s1随h/r变化的规律Fig.4 The distribution of parameter s1 with h/r increasing

为了准确获得()函数的具体形式，取的几何平均值进行分析(在相同条件下)。根据最小二乘法，最终拟合的()函数具体形式为

(23)

其中

(24)

并且，拟合函数的相关系数为0.9997，如图4中曲线()所示。因此，最终获得了函数的具体形式如下

=()

(25)

5 结果分析与讨论

(26)

其中

(27)

图5 无量纲弯曲角频率ω2随h/r的变化规律Fig.5 The variation of the second-order dimensionless bending angular frequency ω2 with h/r increasing

图6 进动系数K随h/r的变化规律Fig.6 The distribution of the precession coefficient K with h/r increasing

此外，考虑到拟合()的复杂性，为了便于工程应用，本文还研究了=0的特殊情况(即=0时)，获得了二阶弯曲角频率及进动系数的简化理论解，如图5及图6所示。此时，根据式(16)、式(17)和式(18)，从而有截面剪力(,)=0，截面转角(,)≠0，即环结构剪力为零时，仍存在截面转角的变化。根据图5和图6可知，对于二阶弯曲角频率，简化理论解较本文标准理论解大，较经典环理论解小，如当=0.2时，简化理论解较本文标准理论解大1.39%，较经典理论解小0.30%；对于进动系数，简化理论解略小于本文对应的标准理论解，明显小于经典理论解，如=0.2时，简化理论解较本文理论解小0.02%，较经典理论解小0.42%。需要强调的是,虽然基于本文理论的进动系数与经典理论结果的相对误差在0.4%左右，但是这对于高精度谐振陀螺的设计及模型误差分析仍具有重要的指导意义。

通过分析本文理论解中各项所对应的物理内涵，特别是与广义应变的对应关系，发现造成上述差异的根本原因在于，本文的环形谐振子理论不仅可以准确描述结构弯曲变形的能量(特别是广义弯曲应变)，而且可以准确描述结构横向剪切变形的能量(特别是广义剪切应变)：横向剪切变形的大小对于二阶弯曲角频率的理论解有重要影响，弯曲变形的大小对于进动系数的理论解有重要影响。此外，尽管本文简化理论解不能精确表征环结构的横向剪切变形，但可以描述结构的弯曲变形。令人遗憾的是，经典环形谐振子理论由于无法精确表征环形结构的横向剪切变形及弯曲变形，因此对应的二阶弯曲角频率和进动系数理论解都不够准确。

6 结论

本文从环形谐振子结构的线性位移模式出发，基于Timoshenko理论，获得了环形结构的广义应力、应变及本构关系，根据哈密顿原理，建立了考虑横向剪切效应的环形谐振子理论，包括广义本构关系、平衡方程和周期性边界条件等。然后根据布勃诺夫-伽辽金法，推导出包含待求参数的环形谐振子二阶弯曲角频率和进动系数的理论解。接着根据有限元法及最小二乘法，利用获得的二阶弯曲角频率来拟合待求参数()的函数形式。在此基础上，忽略项，获得了简化理论解。最后，对比和分析了本文标准理论解与简化理论解各自的优缺点(即=()与=0时)，并揭示了经典环形谐振子理论的不足。

本文的工作表明：1)本文的环形谐振子理论不仅可以描述环结构的弯曲变形，而且可以描述结构的横向剪切变形；2)环结构横向剪切变形和弯曲变形的大小对于二阶弯曲角频率和进动系数的理论解取值具有重要的影响；3)环形谐振子的进动系数不是恒定的，它会随着的增大而缓慢地减小；4)本文的简化理论解不仅求解方法简单，而且可以准确描述进动系数的大小。此外，本文建立的谐振子新理论不仅可以为高精度谐振陀螺的设计提供理论支撑，而且可以为谐振子误差分析模型提供新的视角，特别是在密度和品质因数的不均性、加工误差及高过载等因素引起的误差分析方面。因此，本文的研究工作具有重要的工程意义和学术价值。