基于离散切比雪夫变换及LT编码的水印算法

石红芹， 孙 丹

(1.华东交通大学 软件学院，南昌 330013； 2.江西省计算中心，南昌 330003;3.江西省科技基础条件平台中心，南昌 330003)

0 引 言

互联网发展极大地促进了网络多媒体作品传播的时效性和范围，数字水印正是为保护版权人的利益不受到侵害，应运而生的一种版权保护技术。数字水印技术是将作者或者版权人独有的标识信息或者序列号嵌入其数字作品当中，既不影响原作品的使用价值也不容易被探知和修改[1]。一旦发生版权纠纷，可通过提取其中的水印信息来验证作品的所有权，也可通过水印比对证明作品是否遭受了恶意篡改，达到版权保护和验证的目的。如何有效地对数字多媒体作品进行版权认证和对被恶意篡改的多媒体作品进行检测，一直是当今研究的热点问题[2-4]。

Tirkel[5]率先提出数字水印的概念，Van-Schyndel等[6]给出数字水印的基本模型，根据信息隐藏方式的不同，数字水印技术主要分为空间域和变换域两类方法[7-8]。由于变换域算法对各类几何攻击具有很好地健壮性，对图像的噪声、旋转、压缩的抗攻击力比较强，故此类算法研究比较多。常见的变换域水印算法有：Cox等[9]提出的将水印信息嵌入到载体图像离散余弦变换(discrete cosine transform, DCT)域的低频分量上；Hsieh等[10]研究了一种基于离散小波(discrete wavelet transform, DWT)域的数字水印算法，对载体进行DWT变换，控制变换后频域分量系数的熵自适应地嵌入水印信息；Liu等[11]将宿主数据分块后分解为幅值信息和相位信息，将水印数据嵌入到分解所得的相位信息中的离散傅里叶变换(discrete fourier transform, DFT) ，算法具有很好地防篡改性能；离散切比雪夫变换(discrete tchebichef transform, DTT)基函数[12]的特性与离散余弦变换类似，故此DTT也广泛应用在数字图像重建领域。

变换域水印算法的缺陷就是嵌入信息量比较小，为解决这一问题，本文提出一种基于离散切比雪夫变换的水印算法，文中水印信息使用了载体图像的QR码， QR码的特点就是纠错能力强且自身容量大[13]，将其作为水印嵌入到载体中，既能增强水印算法的鲁棒性又能提高水印信息的嵌入量。在水印信息提取阶段，通过将提取水印信息与发送到可靠第3方保存的原始水印信息的阈值比对可以实现算法的篡改检测。

1 背景研究

1.1 离散切比雪夫变换

切比雪夫矩是2001年由Mukundan等[14]提出的。而切比雪夫多项式[15]则是以递归方式定义的序列。该序列具有快速迭代的特点，被广泛地应用于图像处理和分析领域。归一化离散切比雪夫多项式：

(1)

n=2,3,…,N-1

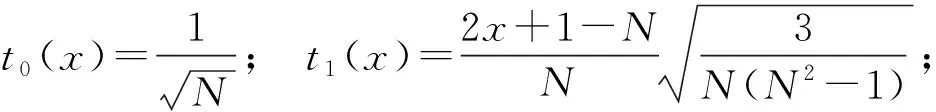
图1所示为0～5阶离散切比雪夫多项式归一化后的曲线。

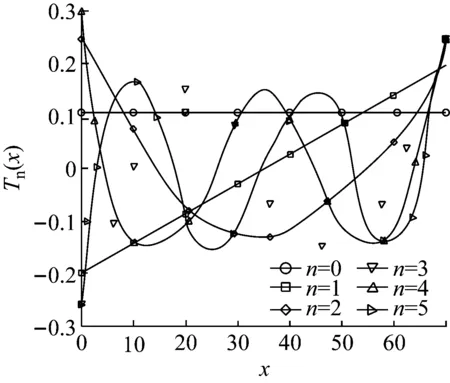
图1 归一化的0～5阶离散切比雪夫多项式曲线

图像f(x,y)切比雪夫变换多项式：

(2)

式中：m=0,1,…,M-1；n=0,1,…,N-1。在实际应用过程，数字图像的DTT变换与反变换矩阵

(3)

式中：F为变换到DTT域的图像；f为空间域的图像；C1与C2皆为正交可逆矩阵。若M=N，则有C1=C2=C，且满足CT=C-1

1.2 LT编码

LT码是由Luby[16]提出的一种实用型喷泉码，具有良好的纠删性能。在码率为m/n的情况下，传输一个包含mbit的信息用LT编码器可以生成nbit编码。

由m个待编码信号(水印数据bit)Y=[y1,y2,…,ym]T生成n个编码信号Z=[z1,z2,…,zn]T的过程如图2所示。

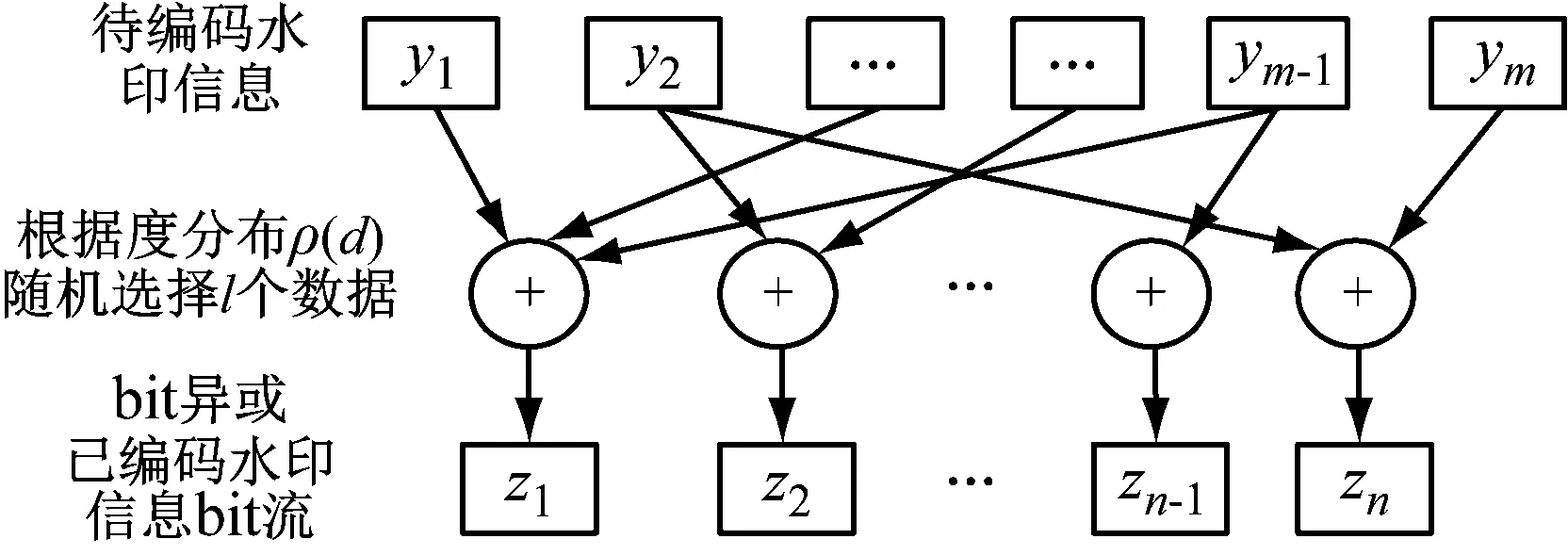
图2 LT码编码示意图

(1) 根据选定的度分布函数ρ(d)(d=1,2,…,m)随机选择一个数据bitdi(1≤di≤m)的度为l。

(2) 从m个待编码的数据bit中等概率选取l个不同的待编码数据bit并将其进行异或得到一个已编码数据bit。

(3) 重复(2)的操作即可得到n个已编码数据

bitZ=[z1,z2,…,zn]T

2 算法描述

2.1 水印嵌入算法

本文算法水印嵌入及提取过程示意如图3所示。

(1) 对大小为M×M的灰度载体图像O进行n×n非重叠分块，随机选取不同行不同列的n个分块作为嵌入块，构成嵌入数组Q(保存嵌入数组中所有分块的坐标值为密钥key1作为水印提取的依据)。

(2) 对嵌入数组中的所有分块Qi做2级离散小波变换，提取其低频系数矩阵fiLL2(x,y)。

(3) 对每个嵌入块的低频系数矩阵fiLL2(x,y)进行离散切比雪夫变换(DTT)

(4)

对DTT的变换矩阵Ci进行奇异值分解

(5)

(4) 提取载体图像O的QR码作为待嵌入水印w，将QR码发往可靠第3方保存，再对QR码图像进行Arnold变换

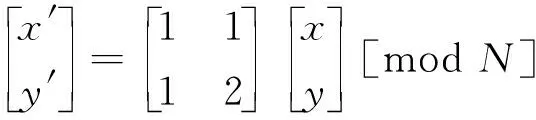
(6)

式中：(x,y)为QR码图像矩阵的某个像素点未变换时的位置；(x′,y′)为Arnold变换后的新位置，变换次数作为密钥key2保存。

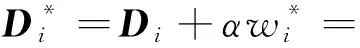
(7)

式中,α为水印的嵌入强度，依据经验值α=0.28。

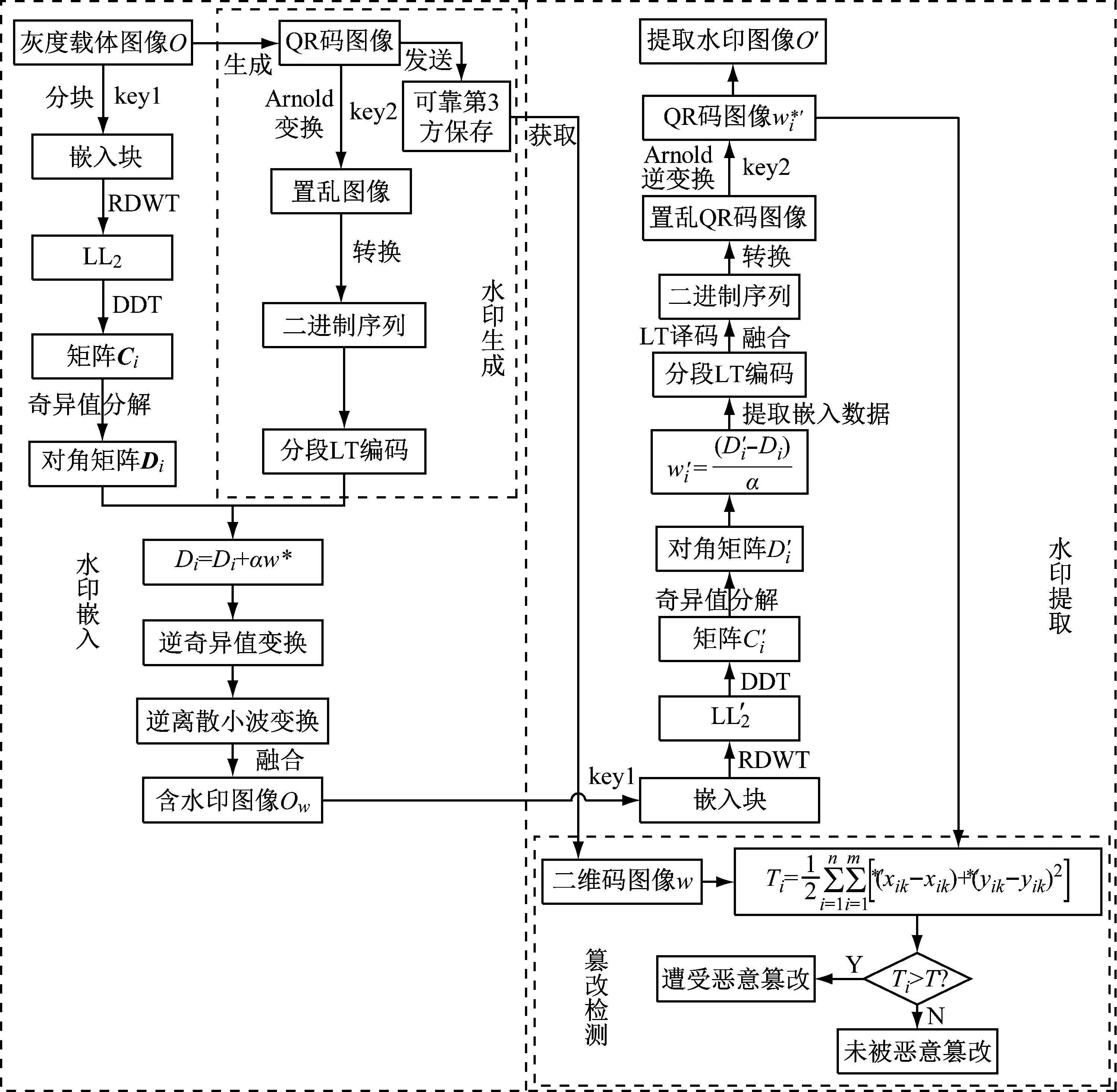
图3 水印嵌入及提取流程图

经过奇异值逆变换后得到新的DTT变换矩阵

(8)

经过逆DTT变换后得到含水印图像的低频分量

(9)

(10)

再经过一系列的逆奇异值变换、逆离散切比雪夫变换及逆离散小波变换后得到含水印图像Ow。

2.2 水印提取算法

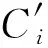
(11)

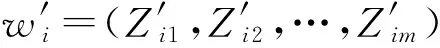
(12)

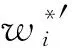
(13)

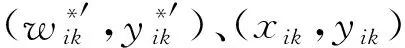
T=t1+γt2

(14)

式中：t1为合法操作强度；t2为非法篡改引起的最小扰动；γ为与扰动相关的系数。

3 仿真结果与分析

本文通过仿真对算法的鲁棒性和透明性进行验证。如图4所示，载体图像选用了256×256的灰度图像Cameraman。图5为载体图像Cameraman的QR码作为水印图像，图6为水印的置乱图像。

使用归一化相关系数NC作为算法性能验证的客观依据，由经验可知NC的值越大说明算法的鲁棒性能越好；而峰值信噪比PSNR被用来衡量图像视觉特性即嵌入水印后图像的失真情况，一般PSNR值越大说明水印的透明性越好即失真度越小。

3.1 算法透明性检测

实验分为3组，对大小为256×256载体图像Cameraman进行等面积非重叠分块，如图7所示载体图像被分割成n×n分块的3组(n值分别取4、8、16)，每组都随机选取不同行不同列的n个分块构成一个嵌入数组Q，将分段编码后的水印信息按照文中2.1所述算法嵌入到数组Q的每个嵌入块中。图8所示为含水印载体图像，从视觉上看不出载体图像的变化。

(a) 4×4分块

(a) 4×4分块

表1所示为不同分块情况下含水印图像在未受攻击时PSNR和NC值，由表1可知，所有分组的PSNR均大于40 dB，这说明算法的失真度很小具有很好地透明性。

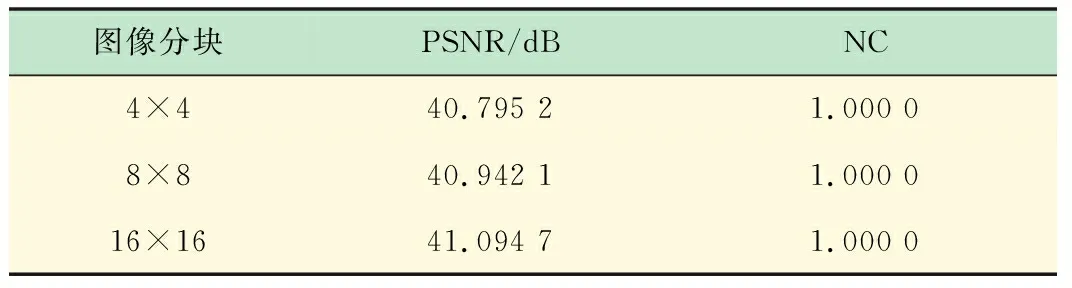
表1 图像嵌入水印的测试结果

3.2 水印算法的鲁棒性检测

图中仿真实验以对载体图像进行8×8分块为例，对含水印图像进行不同的几何攻击后提取水印图像并测算其NC值。

图9所示为含水印图像在受到不同类型攻击后提取并恢复的水印图像，从视觉上都可以清晰地分辨出水印图像，根据仿真数据可以判断出本文算法具有很好的鲁棒性。

表2给出了算法对载体Cameraman进行不同比例分割的情况下，含水印图像受到各类几何攻击时分别提取的水印图像的NC值与文献[17]提取的水印图像NC值对比。由表中数值可见，本文算法在高斯低通滤波、中值滤波、缩放，剪切等方面的性能都优于文献[17]。

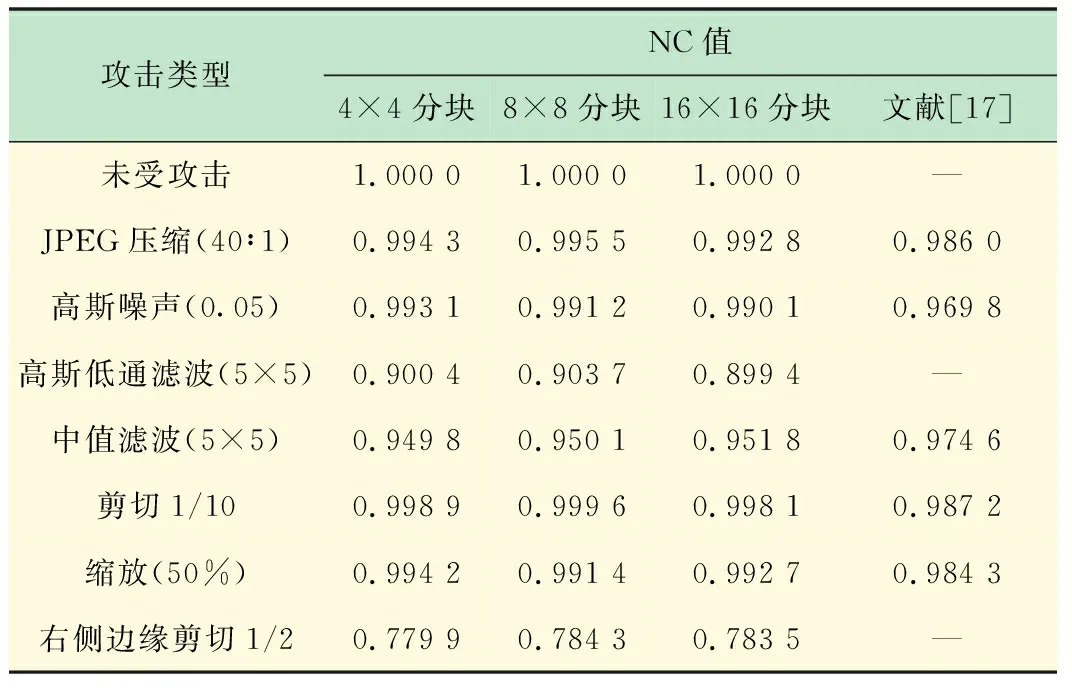
表2 本文算法与文献[17]NC值对比

4 结 语

本文结合QR码、LT编码及切比雪夫变换技术提出了一种防篡改的数字水印算法。首先因为LT编码具有良好的纠删性能极大地提高算法抗剪切能力，由于嵌入数组选择了不同行不同列的分块构成，使得载体受到剪切攻击时的损失最小化，通过原始载体QR码和提取QR码信息的比对，可进一步印证图像是否遭受过篡改攻击，仿真实验的数据也印证了算法对剪切、噪声、滤波、JPEG压缩等攻击都具有良好的鲁棒性，同时含水印图像的PSNR值也说明了算法具有很好的透明性。下一步研究的重点是如何更好地降低算法的时间复杂度。