VR 全景视频时空切片传输的流量评估与建模

韩圣千，娄函，王君来

（北京航空航天大学电子信息工程学院，北京 100191）

0 引言

虚拟现实（VR,virtual reality）全景视频被认为是未来移动通信系统高带宽需求的主要应用场景之一[1-2]。为了满足良好的用户观看体验，VR 全景视频具有很高的画质要求，对未来移动通信系统的传输性能提出了严峻挑战[3]。

基于时空切片的VR 全景视频传输是一种减轻通信系统传输压力的有效手段之一[4]。图1 给出了VR全景视频时空切片传输示意，其中，空间切块参数t=3，时间分段长度d=3。其基本思想如下。1) 在空间维，考虑到用户只会观看全景画面的一部分，而未被观看的部分可以不传输，为此将每帧画面空间切分为视频块（Tile），然后根据用户当前的视点，只传输视域（FoV,field of vision）范围内的切块[5]。2) 在时间维，为了适应通信系统传输速率的动态变化，视频通常被切分为多个视频段，每一段进行独立的压缩编码，作为一个独立单元进行传输，例如基于HTTP的动态自适应流（DASH,dynamic adaptive streaming over HTTP）技术。基于时空切片传输，系统只需在每个时间分段里传输视域范围内的空间切块，可以大大减轻系统传输负担[6]。

针对空间切块传输，文献[7]研究了切块数量对画面质量的影响，比较了不同切块数量下的画面峰值信噪比（PSNR,peak signal to noise ratio）。文献[8]观察到用户在观看VR 视频时很少关注画面的上方和下方，提出了非均匀空间切块方式，结果表明非均匀空间切块可以节省更多的带宽，但会降低视频压缩的性能。文献[9]基于观众对视频画面不同区域的访问概率以及画面内容，提出了一种自适应空间切块方式，可以有效降低系统的带宽需求，但实现复杂度较高。文献[10]考虑用户视点的非理想预测，评估了空间切块传输相对于非切块传输对视角内PSNR的提升作用。针对时间分段传输，文献[11]研究了在给定压缩编码率条件下，时间分段的长度对全景视频画面质量的影响。文献[12]针对空间切块传输，对每个时间分段的视频编码率进行了优化。文献[13]在每个时间分段内为视点中心和边缘的空间切块设置不同的视频编码率，从而降低传输流量。针对传统二维视频，文献[14-15]研究了在给定时间分段方式时如何根据通信条件的动态变化来自适应地选择每个分段的视频质量。

现有文献在研究时空切片传输方式如何影响VR 全景视频传输流量时，主要考虑了传输画面减少带来的流量节省[16-17]。然而，空间切块和时间分段的方式对传输流量有着复杂的影响。首先，空间切块并不一定越多越好。一方面，切块数量越多，实际传输的画面面积越小，这有利于节省流量；另一方面，每个空间切块都是独立压缩编码的，画面切分得越小，则利用画面空间相关性进行视频压缩的效率越低，导致每个切块的压缩率下降。综合考虑两方面因素可知，增加切块数量并不一定导致传输流量下降。其次，时间分段也不一定越长越好。一方面，分段越长，则利用画面时间相关性进行视频压缩的效率越高，有利于降低视频传输流量；另一方面，对于时空切片传输而言，增加时间分段长度可能会导致传输更多的切块，从而增加传输流量。例如，在图1 中，每个时间分段长度包含3 帧画面，如果用户在观看整个分段时视点保持不变，如时间分段1，则只需传输FoV 包含的{4,5,7,8}这4 个空间切块即可；但是如果用户在观看过程中发生了头动，如时间分段 2，则此时需要传输{4,5,6,7,8,9}这6 个空间切块。时间分段越长，那么用户在一个时间分段内发生头动的概率越大，可见时间分段长度并不一定越大越好。

图1 VR 全景视频时空切片传输示意

为了分析和刻画VR 全景视频的传输流量需求与时空切片方式之间的复杂关系，首先，基于实际的VR 全景视频观看数据集，通过仿真来分析和评估时空切片方式对传输流量需求的影响。然后，基于仿真结果，对传输流量需求进行统计建模，建立统计模型参数与时空切片方式之间的函数关系。最后，基于建立的模型，提出一种时空切片方式的优化方法，最小化VR 全景视频的传输流量。仿真结果表明，基于所建立的模型得到的时空切片方式可以获得接近最优的性能。

1 VR 全景视频的传输流量需求评估

本文采用开源VR 全景视频观看数据集进行仿真分析，文献[18]对相关数据集进行了总结和对比。通过比较各个数据集的规模（定义为用户数×视频数×时间长度），本文选用其中规模较大的数据集[19]。该数据集在各研究中得到广泛应用，例如文献[20]使用该数据集进行VR 用户的头动和视点预测；文献[21]利用该数据集中不同用户观看相同视频的头动相关性来预测用户视点；文献[22]基于该数据集分析了不同用户观看视频时的头动相关性，并对提出的头动预测方法进行了性能评估；文献[23]采用该数据集对提出的基于深度强化学习的全景视频传输策略进行训练和用户体验质量（QoE,quality of experience）评估；文献[24]提取该数据集中的用户头动信息来训练神经网络预测用户视点。

该数据集包含3 个表演类视频（编号1、4、7）、3 个运动类视频（编号2、5、8）、一个电影类视频（编号3）和2 个纪录类视频（编号6、9）。所有视频均未进行时空切片，投影方式为等距柱状投影（ERP,equi-rectangular projection），分辨率为2 560 像素×1 440 像素，帧率为30 帧/秒，视频时长范围为120～160 s。每个视频包含48 个用户的观看头动记录，每条记录由时间戳、描述头盔显示设备旋转的四元数，以及描述头盔显示设备平移的空间坐标等元素组成。

为了评估传输流量，需要对数据集中的VR 全景视频进行时空切片，然后对每个时空视频块进行压缩编码，并在此基础上引入用户头动数据，最终获得在任意给定时空切片方式下的实际传输流量数据。为此，本文采用FFmpeg的裁剪（Crop）功能[25]来实现画面的空间切块。当空间切块参数为t时，画面横向和纵向分别被等分为t块，得到总切块数为t2。视频的时间分段采用H264 编码器来实现，当分段长度为d帧时，则指定H264 编码器[26]的画面组（GoP,group of picture）参数为其中，对于VR 全景视频，为了降低解码时延，在进行压缩编码时通常不采用B 帧，而只采用I 帧和P 帧，因此每个GoP 由一个I 帧和d− 1个P 帧组成。完成编码的时空视频块经过MP4 Dash 工具[27]处理后，转换为流媒体格式进行存储。对于用户观看每个视频的视点数据，采用数据集中头盔显示设备的四元数换算得到。首先，由数据集的四元数换算为空间三维坐标系中的用户视点方向向量；然后，根据ERP 格式全景视频的映射规则得到平面二维坐标系中的用户视点坐标。最后，根据所得的视点坐标，从画面中提取对应的空间切块，用于后续的仿真评估。

1.1 空间切块对全景视频压缩率的影响

如前文所述，增加空间切块数量会减小每个切块画面的大小，导致利用画面空间相关性进行视频压缩的效率降低。对于任一视频，给定空间切块参数t，分别设置时间分段长度d为30 帧，对该视频进行时空切片并进行压缩编码，得到压缩后的视频大小。计算该视频在30 帧分段长度d下的视频大小的均值，记为Qt。表1 给出了运动类和表演类视频切块后（t>1）视频大小相对于未切块（t=1）视频大小的增长百分比，即

从表1 可知，切块后视频的大小相对于未切块视频均有不同程度的增加。当切块参数为t=6时，视频大小增幅最高接近12%。可以发现，随着切块数的增加，视频大小并非单调增加。这是因为不同的切块数下，每个空间切块包含的画面内容会发生变化。例如，t=4时的切块画面不一定包含在t=3时的切块画面里。但是，由于t=4时的切块是对t=2时的切块的二等分，可知t=4时的切块画面一定包含在t=2时的切块画面里，导致t=4时的视频大小一定比t=2时大。同理，t=6时的视频大小一定比t=3时大。

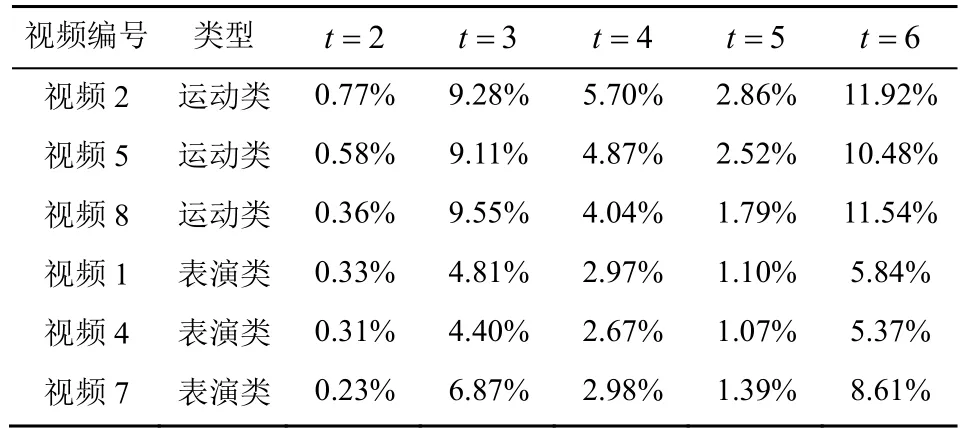
表1 切块视频相对于未切块视频大小的增长百分比

1.2 时间分段对视频压缩率和头动次数的影响

通过分析图1 可知，增大时间分段有助于提高视频的压缩效率。图2 给出了不同时间分段长度（即GoP 长度）的归一化视频大小，其中归一化因子是分段长度为1 帧时的视频大小。从图2 中可以看出，随着分段长度的增加，视频的压缩率首先会快速提升，然后逐渐放缓。

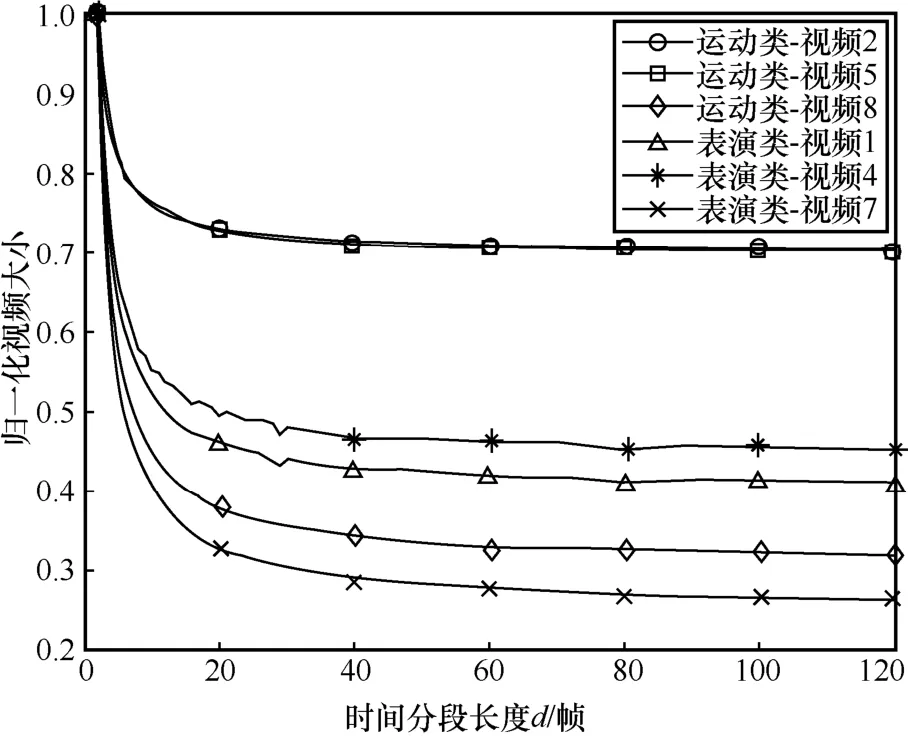
图2 不同时间分段长度的归一化视频大小

时间分段长度增加的另一方面影响是增加用户在观看一个分段过程中发生头动的概率，进而导致需要传输的空间切块增多。图3 对此进行了评估。首先，在评估中，头动发生的定义是用户在1 ms内视点偏移大于1°。在此定义下，给定时间分段长度，针对每个视频包含的所有时间分段，提取对应的48 个用户的观看头动记录，分别统计所有分段内头动发生的次数，进而计算头动次数的均值并作为该视频在当前分段长度下的头动次数。

图3 不同时间分段长度内的平均头动次数

从图3 可以看出，对于所有的视频，一个时间分段内的平均头动次数随着时间分段长度的增加线性增长，说明需要传输的空间切块数随着时间分段长度的增加相应增长。对于表演类视频，用户视点主要集中在舞台上的表演，用户发生头动的频次较少。相比而言，用户在观看运动类视频时，由于拍摄画面切换得更加频繁，用户头动次数明显增多。

1.3 时空切片下全景视频传输流量的评估

从以上的评估分析可以看出，空间切块虽然可以减少传输的画面内容（仅传输视域内的画面），但会导致视频压缩效率降低，而增大时间分段长度虽然可以提高视频压缩效率，但同时也会增加需要传输的空间切块数。下面对全景视频在时空切片模式下的传输流量进行仿真评估。

考虑到用户在观看不同类型的视频时具有不同的头动响应，而用户头动直接影响时空切片模式下传输的切片数量，因此在仿真中使用4 个不同类型的视频，即运动类视频2、表演类视频7、电影类视频3和纪录类视频6。

图4 给出了数据集中48 个用户在观看运动类视频2 时，视频采用不同的空间切块参数（t=1～11）和不同的时间分段长度（d=1～60）进行时空切片时的平均传输流量。从图4 中可知，随着t的增加，传输流量并非一致增加。这与第1.1 节的分析一致，说明当t较小时，空间切块带来的传输画面减少起主导作用，而当t较大时，空间切块导致的压缩率下降起主导作用。对于时间分段，可以看出当空间切块参数较大（如t≥ 2）时，传输流量随着时间分段长度的增加先下降后上升。这是因为当分段较短时，分段长度对压缩率的影响显著，如图2 所示；而当分段较长时，分段长度增加导致的传输切块数增多的影响起主导作用。从图4 中可以看出，运动类视频2 在t=10，d=11时可以获得最低的平均传输流量，相比于未进行时空切片（t=1,d=1）的传输流量节省77.1%。

图4 运动类视频2的平均传输流量

图5 给出了表演类视频7的平均传输流量。根据对图3的分析结果，用户在观看表演类视频时的头动频率低于运动类视频。这直接导致在给定时间分段长度内，表演类视频需要传输更少的空间切块，带来比表演类视频更低的传输流量。从图5 中可以看出，表演类视频在t=10，d=27时可以获得最低的平均传输流量，相比于未进行时空切片（t=1,d=1）的传输流量节省90.5%。

图5 表演类视频7的平均传输流量

图6和图7 给出了电影类视频3和纪录类视频6的平均传输流量，从图6和图7 中可以看出与表演类和运动类视频相似的规律，即t和d并非越大越好。例如，纪录类视频6的最优时空切片参数是t=9，d=17。

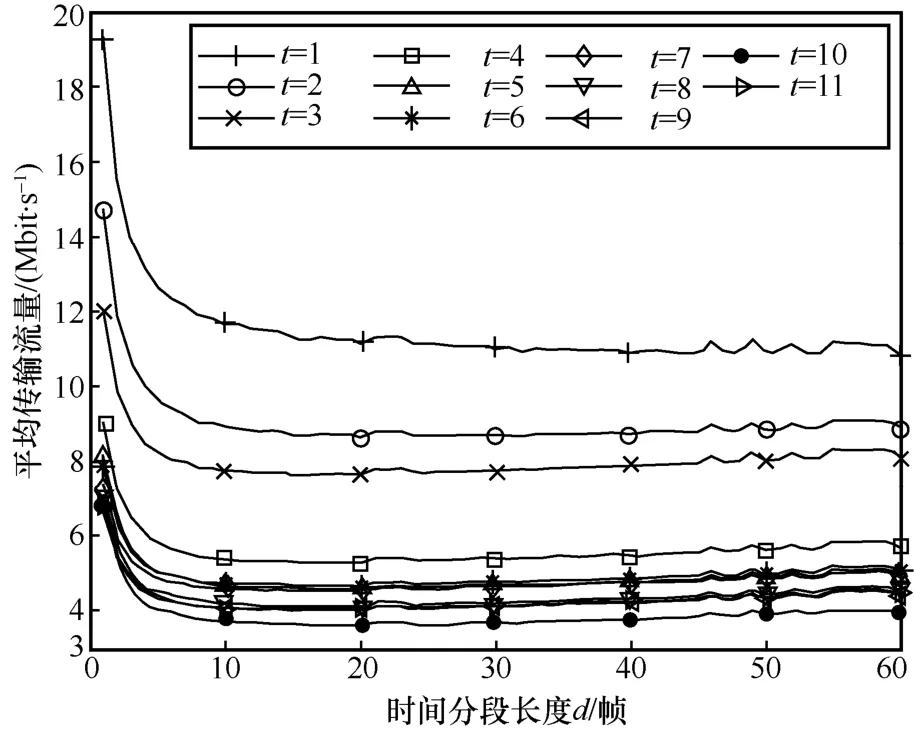
图6 电影类视频3的平均传输流量

图7 纪录类视频6的平均传输流量

2 时空切片传输下的流量建模

基于1.3 节的传输流量仿真评估，本节研究全景视频时空切片传输模式下的流量统计建模。传输流量的建模对象是实际传输给用户的视角范围内的时空切块大小，例如图1 左上方的视频帧只需传输4、5、7、8 切块。可以观察到，传输的切块总大小与2 个因素有关，一是完整视频的大小，二是传输给用户的视角内切块大小占完整视频的比例；两者的乘积即实际传输给用户的业务流量。基于这一观察，下面采用2 个步骤进行建模。首先，针对不同的空间切块数量和时间分段长度，对压缩编码之后的完整视频文件大小进行建模。其次，针对不同的空间切块数量和时间分段长度，根据用户的头动数据，得到用户在实际观看过程中视域范围内的切块大小占完整视频文件大小的比例，并对比例进行统计建模。最后，把完整视频文件大小的模型与视域内切块大小占比的模型相乘，即可得到实际传输给用户的视频切块大小的模型，即传输流量模型。

需要说明的是，根据1.3 节的评估结果，不同类型的视频具有不同的用户头动规律以及不同的最优时空切片方式，因此在进行传输流量建模时有必要针对每类视频单独进行建模。本节提出的传输流量建模方法适用于任意类型的视频，在应用时只需根据不同类型视频的流量样本数据拟合出对应的模型参数。为了评估提出的建模方法的合理性，本节将以运动类视频（其数据集规模大）为例对模型的准确性进行评估。

2.1 视频大小建模

考虑数据集中的某一类视频，在上述仿真过程中已经采用了不同的时空切片方式对这些视频进行了切分、编码、存储，由此可以得到任一时空切片方式下I 帧和P 帧的平均大小。这里的平均是指对所有同类视频的所有I 帧或所有P 帧进行平均。

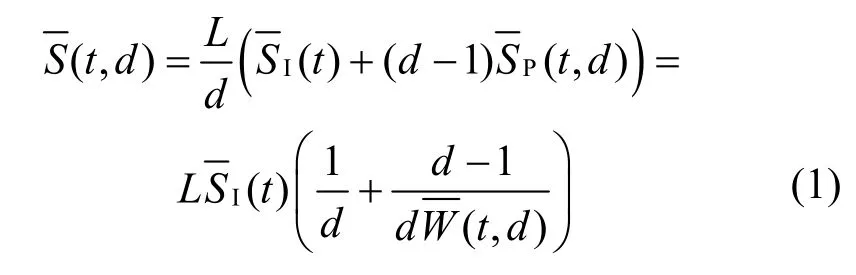
其中，L表示视频包含的总帧数表示视频包含的时间分段数表示I-P 帧平均压缩比，定义为

其中，系数p0和p1可以由现有的线性拟合算法得到。表2 给出了运动类视频的拟合系数。

图8 不同时空切片方式运动类视频的平均压缩比

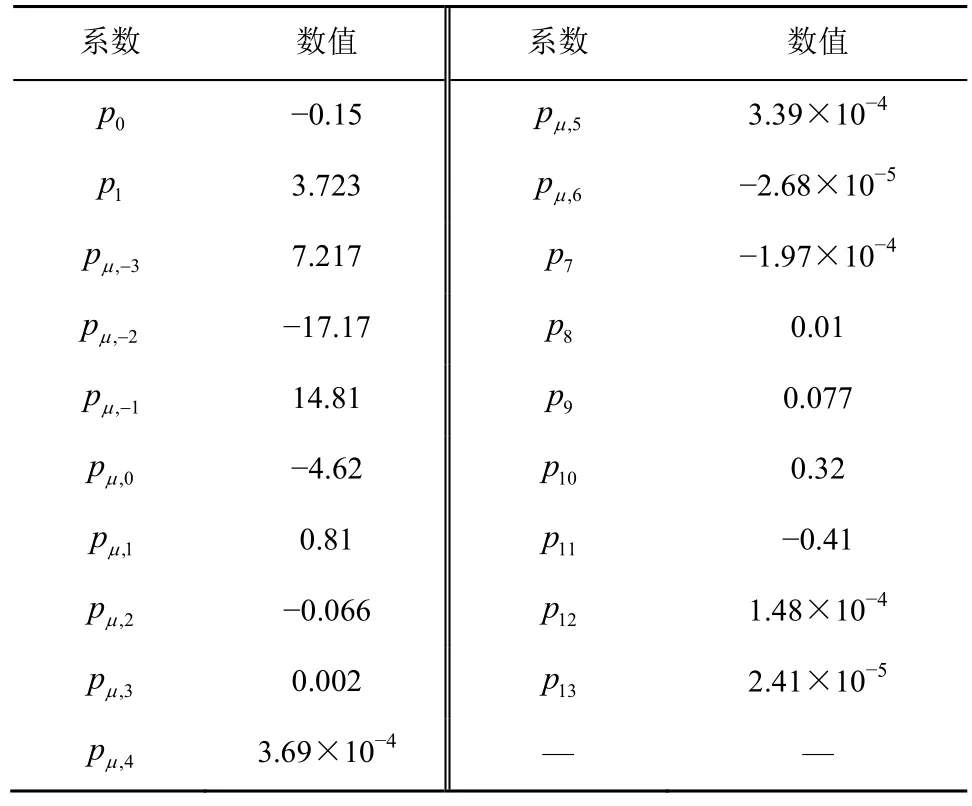
表2 运动类视频的拟合系数

将式(3)代入式(1)，可得视频的平均大小为

表3 不同空间切块参数下I 帧平均大小

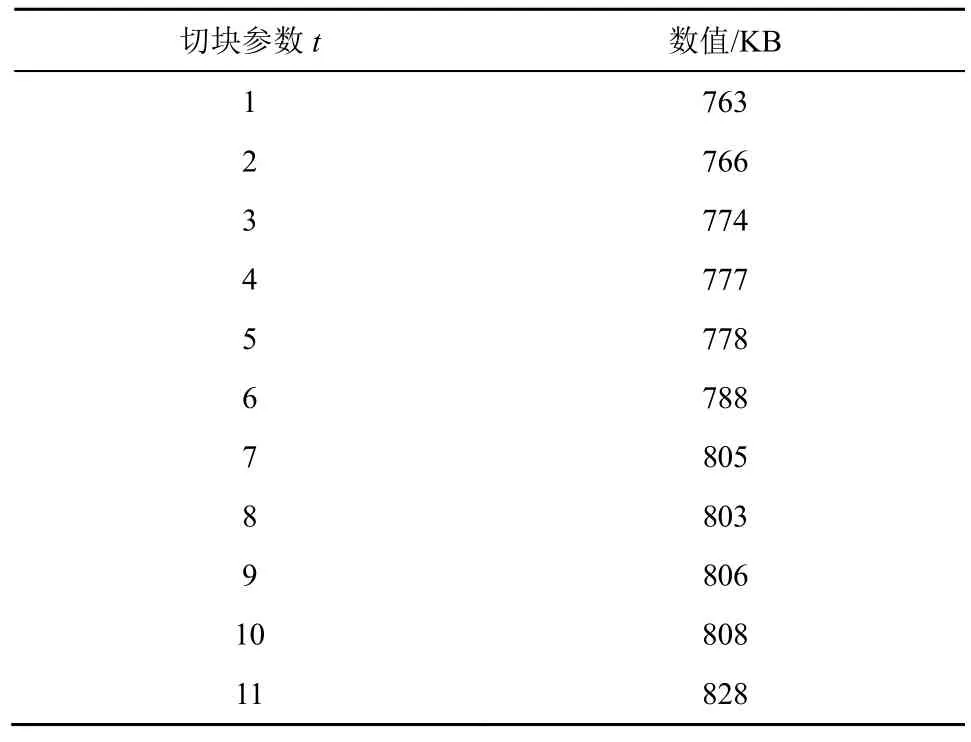
表3 不同空间切块参数下I 帧平均大小

为了验证所建立模型的准确性，图9 比较了式(4)中括号部分的理论计算结果和实际仿真结果。括号部分可以理解为归一化平均视频大小，其中归一化因子是即当所有帧均为I 帧时的视频大小。从图9 中可以看出，对于所有的切块参数t，当分段长度d较大时（例如d>15），由式(4)得到的计算结果与仿真结果很接近，说明了模型的有效性。

图9 归一化视频平均大小的模型准确性

2.2 传输的切块大小占比建模

在前述仿真中，通过引入用户的头动数据，得到了在任一时空切片方式下，用户在观看每个视频时，在每个时间分段内传输的视域内空间切块的大小。由此，可以得到任一用户在观看所有同类视频时，传输的空间切块大小与视频文件总大小之间的平均比例，记为η(t,d)，可以表示为

其中，V表示同类视频的个数表示视频v的第i个时间分段内第j个空间切块是否位于用户的视域内，Sv,ij表示视频v的第i个时间分段内第j个空间切块的大小，因此等号右侧分子项表示需要传输给用户的视域内所有切块的总大小，分母项表示视频文件的总大小。

图10和图11 给出了数据集中48 个用户的平均传输比例η(t,d)的频率直方图和拟合结果，其中前者固定d=15而考虑不同的t，后者固定t=3而考虑不同的d。从图10和图11 中可以看出，η(t,d)的统计分布接近正态分布。因此，采用如下的正态分布对η(t,d)进行建模

图10 传输比例 η(t,d)的频率直方图和拟合结果（d=15）

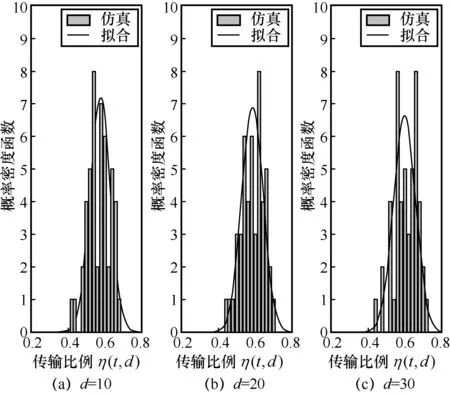
图11 传输比例 η(t,d)的频率直方图和拟合结果（t=3）

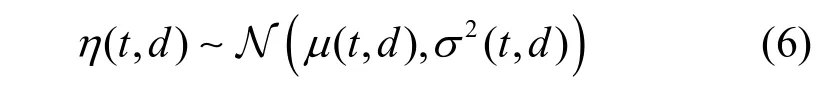
其中，均值和方差均与时空切片方式有关。

为了刻画均值和标准差与时空切片方式的函数关系，针对t和d的不同取值，通过正态分布拟合找到对应的均值和标准差。均值拟合结果如图12所示，标准差拟合结果如图13 所示。其中，黑点代表数据集的仿真结果，曲面代表拟合结果。

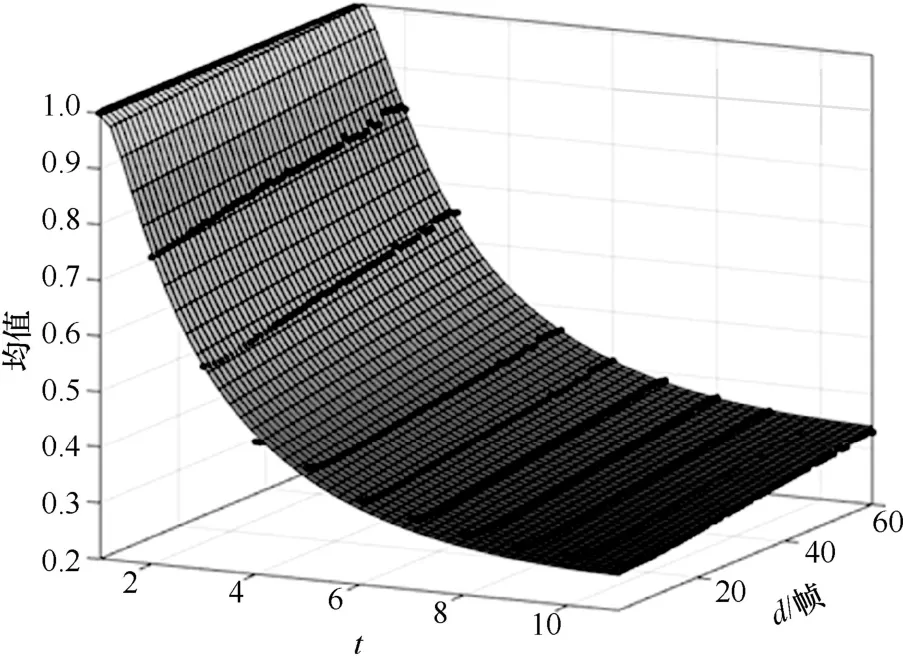
图12 均值拟合结果

图13 标准差拟合结果

通过对图12和图13 进行二维函数拟合，得到均值和标准差与时空切片方式可以近似表示为

式(9)～式(12)中的拟合系数可以使用MATLAB曲线拟合工具得到，具体内容如表2 所示。

将式(7)和式(8)代入式(6)，可以得到传输比例η(t,d)的统计分布。从图10和图11 中可以看出，所建立的统计模型的拟合结果与频率直方图之间具有较高的匹配度，验证了模型的准确性。

将视频平均大小模型式(4)和切块大小占比模型式(6)相乘，最终得到时空切片模式下全景视频传输流量的统计模型。

本文采用统计建模方法建立了所有用户观看所有同类视频时的传输流量模型。考虑到近期深度学习在VR 全景视频的用户头动和视点预测[28]、QoE建模[29]、传输策略优化[30]等方面的成功应用，未来本文将研究基于深度学习的传输流量建模方法，采用神经网络挖掘用户的视频观看偏好和视频画面内容的特征，有望更加准确地预测特定用户在观看特定视频时的传输流量。

3 基于传输流量模型的时空切片优化

本节考虑一个未进行时空切片的VR 全景视频，研究如何利用建立的传输流量统计模型，对其时空切片方式（即空间切块参数t和时间分段长度d）进行优化。

3.1 时空切片方式优化

根据待切分视频的类别，找到对应类别或接近类别的传输流量模型参数。在“流量建模”和“时空切片优化”过程中需要已知视频类别，其中前者可直接从数据集中获取视频类别，而后者通常可以从视频的元数据中获取，例如典型视频网站在发布视频或用户在上传视频时通常会被要求标注类型等信息。如果待切分视频是未经压缩的原始视频，则可以直接使用已建立的同类视频模型。如果待切分视频已经在未进行空间切块（t=1）的情况下进行了压缩编码，则可以统计出当前视频的I-P 帧压缩比，记为W。据此，可以对统计模型中的I-P 帧平均压缩比进行修正，以确保当t=1时等于W。修正后的可以表示为

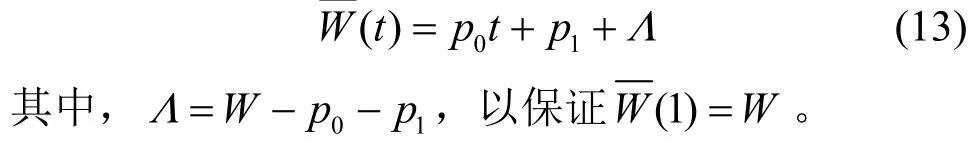
将式(13)代入式(1)，可得待切分视频在时空切片后的大小进而乘以传输的切块大小占比η(t,d)，可得用户观看该视频时需要传输的流量满足如下正态分布

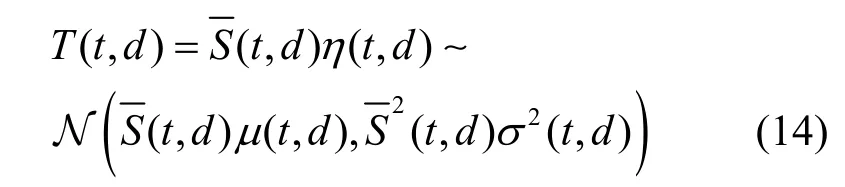
为了区分空间切块参数t和时间分段长度d的影响，将式(1)给出的表示为

从式(16)和式(17)可以看出，首先，空间切块参数t对模型参数有着复杂的影响，体现在等多个函数上；然后，在给定空间切块参数t时，时间分段长度d与模型参数的关系式相对简单，均值和标准差都具有的形式，其中系数θ1～θ3可由式(16)和式(17)得到；最后，均值和标准差都与空间切块参数t和时间分段长度d的交叉项有关（即式(16)和式(17)等号右侧的前两项），因此它们对模型参数的影响不是简单的叠加，而存在相互耦合的关系。

对于随机传输流量T(t,d)，其置信度为ρ∈ [ 0,1]的上界（记为Tρ(t,d)），定义为

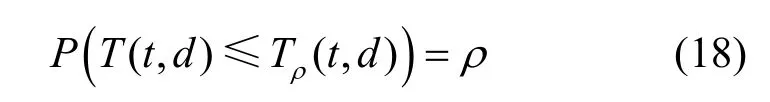
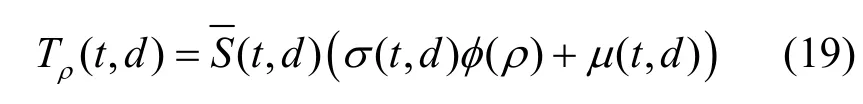
其中，φ(ρ)是标准正态分布的ρ分位点，其数值可以通过查表或数值计算等方式得到。

将式(16)和式(17)代入式(19)，并进行同类项合并，则Tρ(t,d)可以表示为

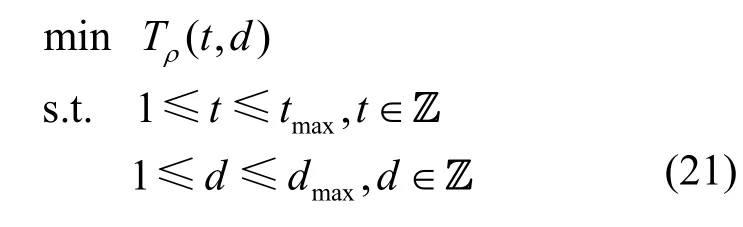
其中，tmax和dmax是系统允许的空间切块和时间分段数的最大值。

由于Tρ(t,d)与优化变量t的关系式很复杂，同时考虑到空间切块参数t的取值范围一般不会太大，因此可以采用遍历的方式对t进行搜索寻优。对于任意给定的参数t，下面计算最优的参数d。

由式(20)可得Tρ(t,d)关于参数d的二阶导数为其正负号在定义域 1≤d≤dmax内只与系数Δ1(t)有关。下面针对Δ1(t)，分3 种情况讨论参数d的最优解。

1)Δ1(t)=0。此时是d的单调函数。如果Δ2(t) ≥ 0，则d的最优解为1，否则为dmax。

综上所述，可以采用内外嵌套方法来求解优化问题式(21)。在外层，对空间切块参数t进行遍历搜索；在内层，针对给定的外层参数t，采用上述优化方法直接计算参数d的最优值，进而得到在当前外层参数t下的函数值，用于遍历寻优。

3.2 仿真结果

本节对所提出的时空切片优化方法的性能进行评估，采用第2 节提出的建模方法，分别使用数据集中的运动类视频和表演类视频来建立传输流量统计模型，针对四类视频分别进行性能评估，包括运动类视频2、电影类视频3、纪录类视频6和表演类视频7。评估中，令tmax=11，dmax=60；置信度选择为ρ=0.9，通过数值计算可得 分位点φ(ρ)=1.28。

为了评估由模型优化得到的时空切片方式与实际最优方式的差距，本节通过仿真得到待切分视频的最优切片方式。具体地，首先，把待切分视频分别按照t=1,2,…,11，d=1,2,…,60的配置进行切片和压缩编码；然后，导入用户的头动数据，获得每一种切片配置下48 个用户观看时的传输流量；最后，绘制48 个用户的传输流量的累积分布函数曲线，找到ρ=0.9时的分位点，即Tρ(t,d)。通过遍历所有的t和d组合，找到使Tρ(t,d)最小的最优时空切片方式。最终得到运动类视频2的最优方式是t=10，d=11；电影类视频3的最优方式是t=10，d=15；纪录类视频6的最优方式是t=9，d=15；表演类视频7的最优方式是t=10、d=27。

在图14 中，本节采用基于运动类视频类建立传输流量统计模型，使用所提出的优化方法求解问题式(21)，得到使目标函数最小的时空切片方式为t=10，d=14。图14 中虚线给出了4 个视频在模型优化方式下的归一化传输流量的累积概率分布，实线给出了4 个视频通过仿真搜索得到的最优切片方式的结果。可以看出，对于运动类视频2和电影类视频3，模型优化的结果与仿真搜索的最优结果很接近。这是因为本文使用了由运动类视频建立的传输流量统计模型，而电影类视频与运动类视频具有类似的用户头动规律。对于纪录类视频6和表演类视频7，由于其视频类型与传输流量统计模型失配，可以看出模型优化的结果与仿真搜索的最优结果存在一定的差距。表演类视频7的差距比较明显，其原因是用户在观看表演类视频时，视线主要集中在舞台上的表演，发生头动的频次较少，这与观看运动类视频时的头动规律差别很大，如图3 所示。这一结果说明对于用户头动规律差别较大的视频类型有必要进行单独的传输流量统计建模。

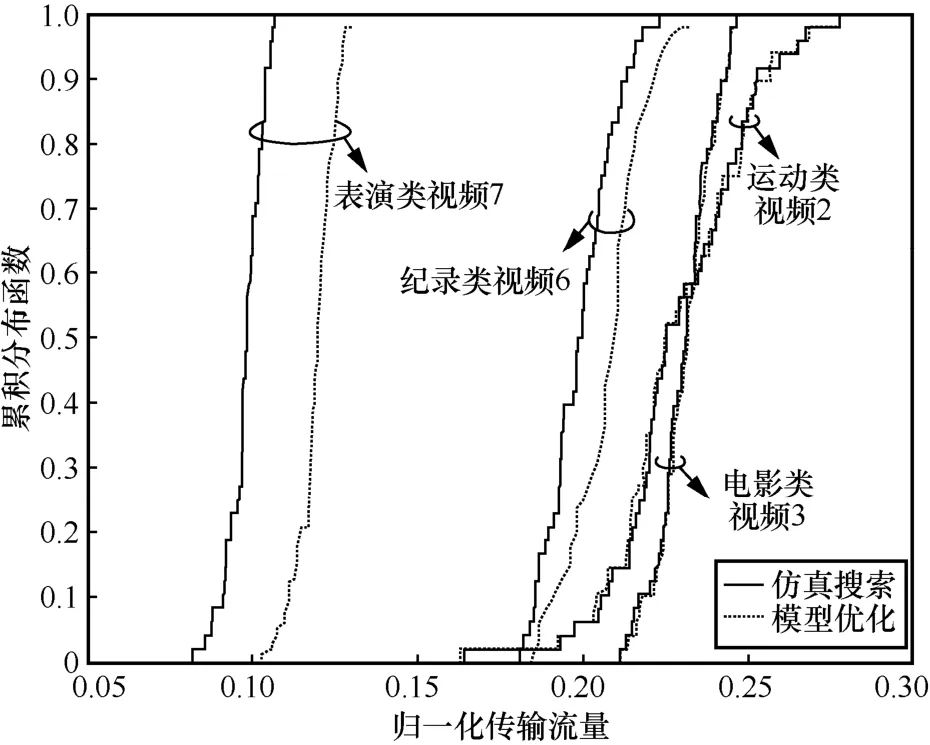
图14 基于运动类视频模型优化的时空切片方式的性能

在图15 中，本节采用表演类视频来建立传输流量统计模型，进而基于此模型求解优化问题式(21)，得到使目标函数最小的时空切片方式为t=10，d=24。通过对比图14和图15 中的表演类视频7，可以看出模型优化的结果与仿真搜索的最优结果之间的差距减小。其他3 类视频由于与传输流量模型失配，导致模型优化的结果与仿真搜索的最优结果之间的差距变大。

图15 基于表演类视频模型优化的时空切片方式的性能

4 结束语

本文针对VR 全景视频传输，研究了时空切片方式对传输流量的影响。首先，基于实际的VR 全景视频观看数据集，通过仿真分析了空间切块数量和时间分段长度对视频大小的影响，并通过引入用户观看头动数据，评估了时空切片方式对全景视频传输流量的影响。然后，基于仿真数据，对时空切片模式下的传输流量进行了统计建模，结果表明传输流量服从正态分布，并建立了均值和标准差与时空切片方式之间的函数关系。最后，基于所建立的统计模型，提出了一种时空切片方式的嵌套优化方法，外层对空间切块数量进行遍历寻优，内层可直接计算最优的时间分段长度。评估结果表明，通过对不同类型的视频分别进行传输流量统计建模，基于所建立的流量模型优化得到的时空切片方式与通过仿真搜索得到的最优切片方式性能接近。