面向调控信息新鲜度保障的电力至简物联网资源优化

廖海君，贾泽晗，周振宇，刘念，王飞，甘忠，姚贤炯

（1.华北电力大学河北省电力物联网技术重点实验室，河北 保定 071003；2.国网上海市电力公司电力调度控制中心，上海 200122）

0 引言

随着整县光伏的大力推进，以及新型电力系统的建设，屋顶分布式光伏建设规模急速扩大，分布式能源迎来爆发式增长。然而，由于光伏等分布式能源具有间歇性、随机性、波动性等特点，高比例分布式能源的并网会对电力系统的潮流分布、电能质量、网络损耗及调节能力造成巨大的影响[1]。因此，需要根据负荷动态调控分布式能源，从而提高新型电力系统的稳定性，实现有功/无功功率的平衡，使光伏等分布式能源得到更好的消纳，避免因消纳困难而出现弃光等现象[2]。

面向分布式能源调控系统，文献[3]建立了兼容需求侧可调控资源的冷热电三联供分布式能源系统经济优化调控模型，并提出了基于量子烟花算法的分布式能源调度方法来降低系统发电成本、环境成本与备用成本。文献[4]考虑高通信时延导致分布式单元状态波动大与调度决策迭代次数增加的难题，设计了基于标准差判断的优化一致性算法，在满足系统有功功率平衡条件下实现了分布式能源调控经济最优化。文献[5]考虑光伏出力不确定性以及规模化调度带来的优化计算压力，提出了一种基于交替方向乘子法的云边协同能源调控方法，能够大幅降低分布式能源调控一致性解的计算复杂度。然而随着分布式能源种类和规模的不断扩大以及源网荷储协同互动参与电网低碳运行需求的提出，传统基于优化理论的分布式能源调度方法面临维数灾难问题，难以通过量化大维度状态空间与调控决策的映射关系获得调控决策模型。

基于机器学习的分布式能源调控模型训练凭借其优越的非线性复杂函数拟合能力与数据挖掘能力，能够通过海量信息来构建和训练负荷需求、光伏出力、气象信息与调控策略之间的模型。信息年龄（AoI,age of information）是衡量信息新鲜度的有效指标，表示信息自产生以来到用于调控模型训练所经历的时延[6]。能源调控信息的新鲜度对模型训练的精度具有重要的影响。当信息年龄较大时，信息的新鲜度、时效性较差，会导致训练模型损失函数大，即模型输出与真实输出之间存在较大偏差，从而降低分布式能源调控的可靠性、经济性、准确性。

借鉴6G 至简无线接入网架构，电力至简物联网具有控制面−数据面分离[7]、融合多模态通信接入的统一架构、跨域资源协同、支持即插即用等优点，可为分布式能源调控决策模型训练所需要数据的采集和传输提供强有力的通信网络支撑，允许物联终端更广泛、灵活、实时地接入网络，并参与分布式能源调控决策模型的训练，提高分布式能源调控决策模型的精度。其中，面对微气象监测、电压/电流/有功/无功全量采集、柔性负荷调控等差异化业务，电力至简网络通过统一的接口设计，支持光照传感器、电压采集器、电动汽车充电桩等终端无差别地接入电力线通信（PLC,power line communication）、无线局域网（WLAN,wireless local area network）、5G 等多模态通信媒介，并充分协同通信、计算、存储等跨域资源实现网络功能按需定制。然而，面向分布式能源调控的电力至简物联网还需要解决如下技术挑战。首先，模型训练与数据传输的耦合导致模型训练过程中需要将大量原始数据上传至中心训练节点，造成网络拥塞、通信资源浪费、本地数据隐私泄露。其次，通信、计算、存储等跨域资源的优化与模型训练的适配性差，导致模型损失函数大，分布式能源调控的准确性与可靠性降低。而跨域资源协同优化涉及大维空间[8]，难以获得精确的概率统计模型与闭式解。最后，调控现场中存在多模态异构网络，终端计算资源与多模态信道质量差异性导致信息年龄增大，难以保障分布式能源调控信息新鲜度长期约束。

目前，针对至简网络的研究主要集中在架构设计[9]、标准化[10]等方面，但是，面向分布式能源调控的电力至简网络模型训练架构，以及保障调控信息新鲜度的跨域资源优化研究还较少涉及。联邦学习是实现智能决策与原始数据传输解耦的一种半分布式学习方法[11]，能够保护本地数据隐私性，已被应用于数字孪生、机器学习等模型训练。文献[12]构建基于联邦学习的数字孪生架构，并提出一种基于多智能体深度强化学习的低时延资源分配（MDRL3RA,multiagent deep reinforcement learning based low-latency resource allocation）算法，通过联合优化信道分配与批量规模策略，在满足学习精度的情况下最小化训练时延。文献[13]提出自适应联邦学习批量规模优化（AFLBSO,adaptive federated learning based batch size optimization）算法，基于近端策略优化，通过优化批量规模最小化全局损失函数。然而，这些文献没有考虑分布式能源调控场景与信息新鲜度保障需求，难以实现跨域资源分配与调控模型损失函数最小化之间的灵活适配。在信息年龄方面，文献[14]提出基于公平的年龄最小化更新卸载策略，通过维持多状态信息新鲜度，实现接收端精准决策。文献[15]提出基于贪婪信道资源编排的全局信息年龄最小化算法，实现信息物理融合系统中各类设备的差异化性能质量保障。但是，上述文献没有考虑时隙间跨域资源分配策略的耦合，不能实现分布式能源调控信息新鲜度长期保障。例如，增加样本批量规模可降低当前模型损失函数，但是也会减少终端可用能量，导致未来信息新鲜度偏差较大。

针对上述挑战，本文提出面向调控信息新鲜度保障的电力至简物联网跨域资源协同优化算法。首先，建立基于联邦学习的半分布式调控模型训练架构，通过数据层本地模型训练与控制层全局模型训练，实现决策优化与原始数据传输解耦，避免大规模数据交互导致的通信资源浪费与网络拥塞。其次，提出基于调控信息新鲜度感知的通信与计算资源协同优化（IFAC3O,information freshness aware-based communication-and-computation collaborative optimization）算法，基于伸缩和与李雅普诺夫优化定理对长期调控模型损失函数最小化问题进行迭代间解耦，利用深度Q 网络（DQN,deep Q network）提高高维优化空间下状态−动作价值拟合精度，通过学习信道分配与批量规模联合优化策略实现通信与计算资源分配协同，基于终端Q 值比较解决多模态信道竞争冲突。最后，所提算法具备信息新鲜度感知能力，能够在缺乏未来信息的情况下通过赤字虚拟队列演进感知每个时隙调控信息新鲜度与规定约束的偏差，并根据偏差动态调整信道分配与批量规模优化策略，降低调控信息年龄，实现调控信息新鲜度长期保障。

1 系统模型与问题构建

面向分布式能源调控的电力至简物联网如图1所示，基于分布式人工智能、控制−数据解耦、统一信令交互、跨域资源融合等技术，实现多模态物联终端异构融合，支撑分布式能源调控决策模型训练。电力至简物联网从下至上可分为数据层、网络层、控制层和业务层。其中，数据层通过在分布式光伏、可控负荷、充电桩等电气设备上部署物联终端，为分布式能源调控决策模型训练提供样本数据和本地模型。网络层包含PLC、WLAN和5G 等多种通信媒介，为数据层和控制层的交互提供通道。控制层通过控制器协调各终端参与决策模型训练，为业务层调控优化提供模型支撑。

图1 面向分布式能源调控的电力至简物联网

本文采用联邦学习架构[16]迭代训练分布式能源调控决策模型，假设共需要T次迭代，集合表示为T={1,…,t,…,T}。每次迭代包括全局模型下发、本地模型训练、本地模型上传和全局模型聚合4 个步骤，如图1 所示。由于下行传输能力强，全局模型下发时延可忽略不计[16]。因此，本文重点考虑本地模型训练、本地模型上传、全局模型聚合3 个步骤。

1.1 本地模型训练

假设存在N个物联终端，集合表示为N={1,⋅⋅⋅,n,⋅⋅⋅N}。第t次迭代中，终端n首先用第t− 1次迭代后的全局模型ωt−1更新本地模型ωn,t−1，即ωn,t−1=ωt−1。随后，终端n利用本地数据集 Dn的部分样本训练本地模型。定义终端n在第t次迭代中用于本地模型训练的样本数量为批量规模βn,t，采用损失函数[17]来量化模型的真实输出与目标输出之间的偏差。定义终端n在第t次迭代的本地损失函数为本地样本的平均损失，即

其中，样本损失函数f(ωn,t−1,xn,m)量化了本地模型ωn,t−1在本地数据集 Dn中第m个样本的输出与最优输出之间的性能差异反映了本地模型ωn,t−1的精度，可用于本地模型更新。基于梯度下降法，终端n的本地模型更新为为损失函数

其中，γ>0为学习步长关于本地模型ωn,t−1的梯度。

定义终端n在第t次迭代的可用计算资源为fn,t，则本地模型训练的时延与能耗分别为

其中，en为能耗系数（单位为 W ⋅ s3/cycle3）[18]，ξn为训练单个样本所需要的CPU 周期数（单位为cycle/sample）。

1.2 本地模型上传

假设存在J个多模态信道，包括J1个5G 信道、J2个 WLAN 信道和J3个 PLC 信道，即。信道集合表示为 J={1,…,J1,…,其中j=1,…,J1为 5G 信道，j=J1+1,…,J1+J2为 WLAN 信道，为PLC 信道。定义信道分配变量为αn,j,t∈ {0,1}，其中，αn,j,t=1表示在第t次迭代中控制器分配信道j给终端n用于上传本地模型，否则αn,j,t=0。在第t次迭代，终端n通过信道j上传模型的传输速率为

其中，η为常数，αn、βn、υn和μn分别为电磁干扰的特征因子、偏斜参数、尺度参数和位置参数。

定义|ωn,t|为本地模型ωn,t的大小（单位为bit），终端n上传本地模型的时延和能耗分别为

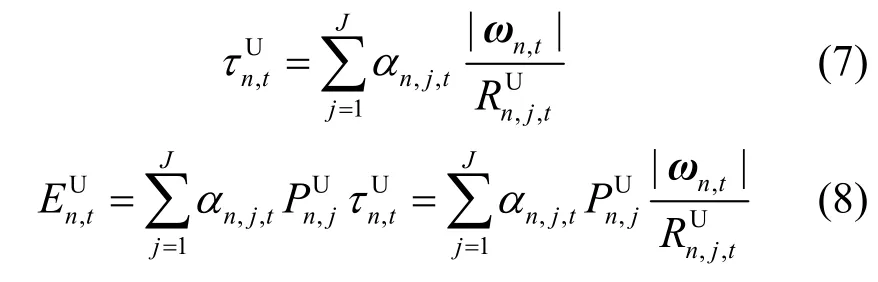
终端n在第t次迭代的总能耗为本地模型训练与上传的能耗之和，表示为

在第t次迭代中，控制器接收到终端n的本地模型所经历的时延为

1.3 全局模型训练

当控制器收到N个终端的本地模型后，基于本地模型加权聚合[20]训练全局模型，表示为

采用全局损失函数[21]来量化全局模型真实输出与目标输出之间的差异，定义为N个终端本地损失函数的加权和，即

1.4 调控信息新鲜度约束模型

调控信息新鲜度是一种信息时效性度量指标，对分布式能源调控的准确性与实时性具有重要影响。调控模型训练时采用的信息新鲜度越高，所生成的调控策略与最优策略之间的性能差距越小。由于控制器在接收到所有终端本地模型后才能开始全局模型训练，调控信息新鲜度与控制器接收到各个终端本地模型所经历的时延密切相关。定义终端n在第t次迭代训练得到的本地模型AoI 为该模型离开终端n到参加全局模型训练的时延，主要包括传输时延和等待时延表示为

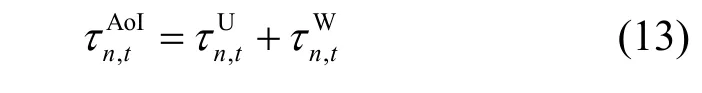
如图2(a)所示，由于终端可用计算资源和通信媒介的差异性，先到达的模型需等待控制器接收到所有终端的本地模型后才能参加全局模型训练，导致调控信息年龄增加与信息新鲜度下降。因此，终端n的本地模型等待时延取决于控制器接收到最后一个终端本地模型所经历时延，即

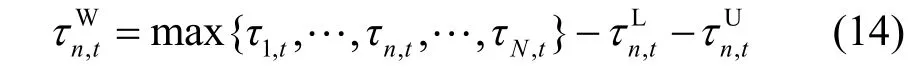
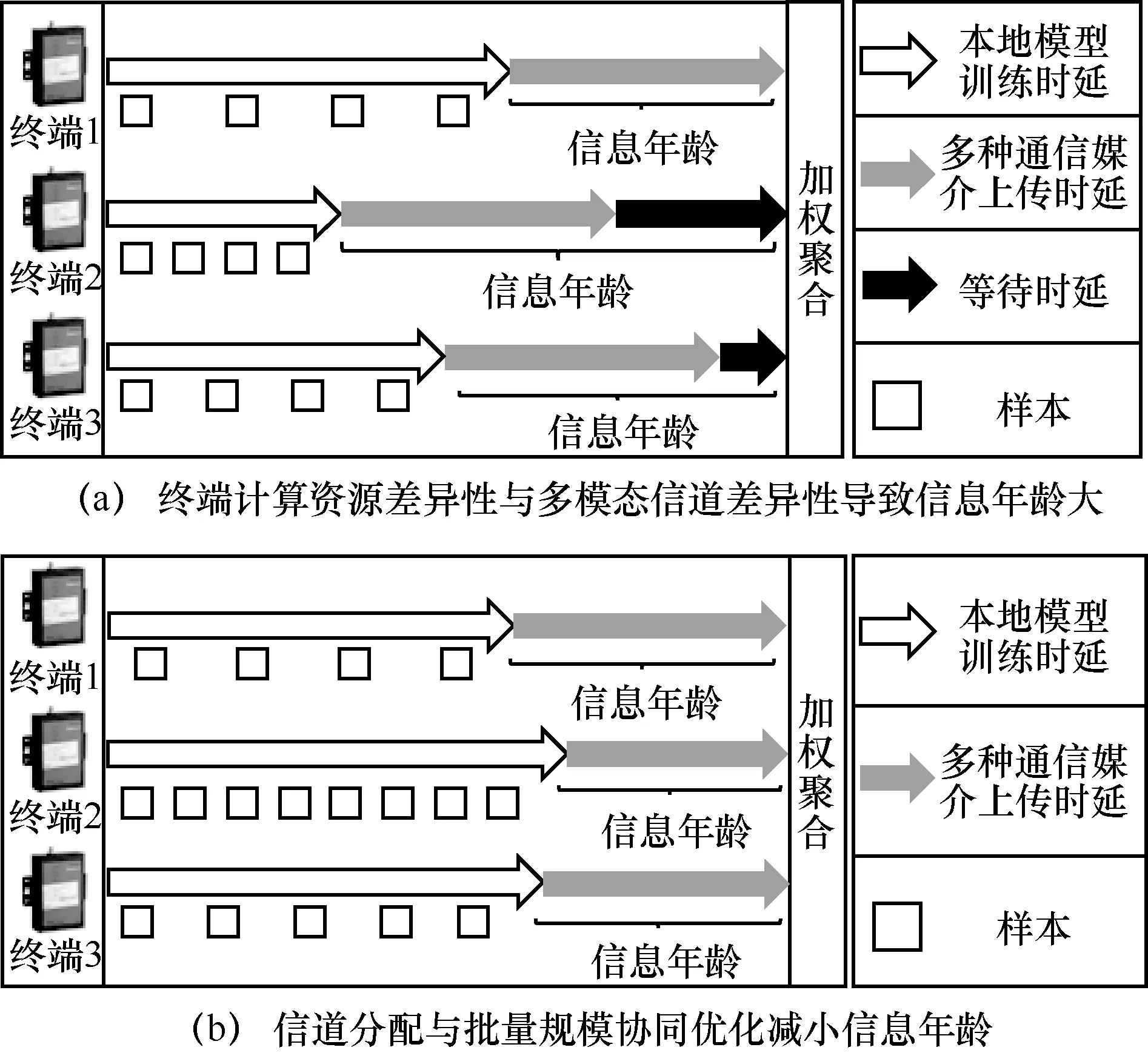
图2 本地训练模型信息年龄示意

定义第t次迭代中终端n的调控信息新鲜度为信息年龄的倒数[22]，即

通过对信息年龄最大的模型进行约束，保障调控信息新鲜度。定义所有终端调控信息新鲜度的集合为ht={h1,t,…,hn,t,…,hN,t}，T次迭代调控信息新鲜度长期约束模型可构建为

其中，hmin为信息新鲜度约束阈值。

对比图2(a)与图2(b)可知，终端差异化计算资源和批量规模导致本地模型训练时延各异，PLC、WLAN和5G等多模态通信方式导致本地模型上传时延不同，通过动态调整多模态信道分配与批量规模策略能够减小信息年龄、提高信息新鲜度。如图2(a)所示，由于终端1 计算性能较差，终端2和终端3 上传的本地模型需要等待终端1 完成本地模型上传后才能被聚合，导致终端2和终端3 信息年龄增大，信息新鲜度低。如图2(b)所示，通过协同信道分配与批量规模，增加终端2和终端3的批量规模并为其分配信道质量更好的5G和WLAN 信道，在消除等待时延、提高全局模型信息新鲜度的同时能够利用更多样本训练全局模型、减小全局损失函数，保障分布式能源调控的准确性与可靠性。

1.5 问题构建

本文旨在解决分布式能源调控决策模型损失函数最小化问题。一方面，增加终端本地批量规模将使本地模型训练更充分，进而降低调控模型全局损失函数，但同时将增大本地模型训练时延和能耗，影响调控信息新鲜度。另一方面，改变信道分配策略会影响终端本地模型上传时延，进而使调控信息新鲜度和传输能耗变化。因此，本文优化目标为在保障调控信息新鲜度等长期约束的同时，通过电力至简物联网通信与计算资源的协同优化，最小化T次迭代后调控模型的全局损失函数F(ωT)。定义多模态信道分配优化变量的集合为αn,t={αn,1,t,…,αn,j,t,…,αn,J,t}，批量规模优化变量的集合为βn,t={1,2,…,|Dn|}，优化问题构建为

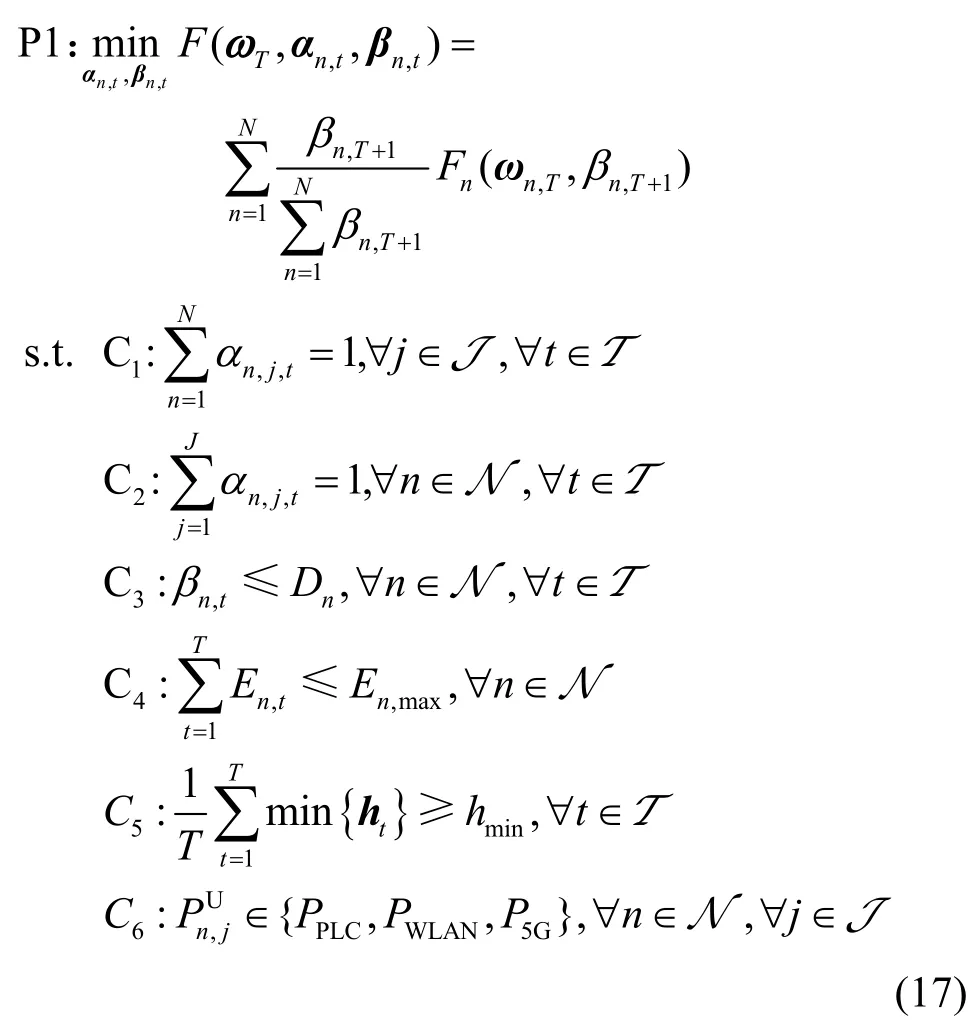
其中，C1表示每个信道只能分配给一个终端；C2表示每个终端只能被分配一个信道；C3表示终端n本地模型训练批量规模约束，|Dn|表示终端n本地数据集 Dn的大小；C4表示终端n的能耗长期约束，En,max表示终端n的长期能量预算；C5表示T次迭代调控信息新鲜度长期约束模型；C6表示终端传输功率约束，PPLC、PWLAN和P5G分别表示PLC、WLAN和5G 信道传输功率。

2 问题转化与算法设计

由于每次迭代的优化策略不仅与T次迭代后的全局损失函数F(ωT)耦合，而且与信息新鲜度等长期约束耦合，导致优化问题P1 难以直接求解，因此需要进行迭代间优化问题解耦。本文首先利用伸缩和定理将长期优化目标解耦为各次迭代中的短期优化目标，并基于李雅普诺夫优化理论将长期约束与短期优化决策解耦，从而将长期随机优化问题解耦为短期确定性优化问题，大幅降低问题优化复杂度。其次，由于解耦后优化问题在第t+1次迭代的状态仅与第t次迭代的状态以及动作有关，而与前t− 1次迭代的状态与动作无关，因此将解耦后的短期优化问题建模为马尔可夫决策过程（MDP,Markov decision process）优化问题。最后，介绍本文提出的算法。

2.1 问题转化

针对第一种耦合，基于伸缩和定理[13]将F(ωT)解耦为

其中，F(ωt−1)在第t次迭代优化时是已知参量。因此，F(ωT)只与第t次迭代的全局损失函数F(ωt)相关，即将F(ωT)的优化转化为对第t次迭代的损失函数F(ωt)优化。

针对第二种耦合，分别构造对应于约束C4和C5的终端能耗赤字虚拟队列Gn(t)与调控信息新鲜度赤字虚拟队列H(t)，其队列积压更新为

其中，Gn(t)表示第t次迭代后终端n的能耗与能量预算之间的偏差，H(t)表示第t次迭代后调控信息新鲜度与信息新鲜度约束hmin之间的偏差。基于虚拟队列理论[23]，当虚拟队列Gn(t)和H(t)稳定时，所对应的长期约束 C4和C5自动成立。进一步地，根据李雅普诺夫优化理论[23]，定义向量ψ(t)=[{Gn(t)},H(t)]，并将李雅普诺夫函数表示为

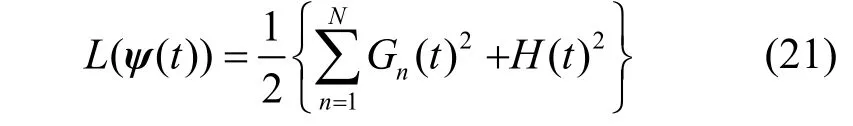
定义李雅普诺夫漂移 ΔL(ψ(t))为L(ψ(t))在连续2 个时隙变化的期望值，因此漂移加惩罚可表示为

将式(21)和式(22)代入式(23)并化简，可得漂移加惩罚的上界为

其中，C为与优化变量无关的常数。因此，问题P1解耦为各次迭代的短期优化问题，优化目标为最大化漂移加惩罚上界的相反数。第t次迭代的联合优化问题表示为

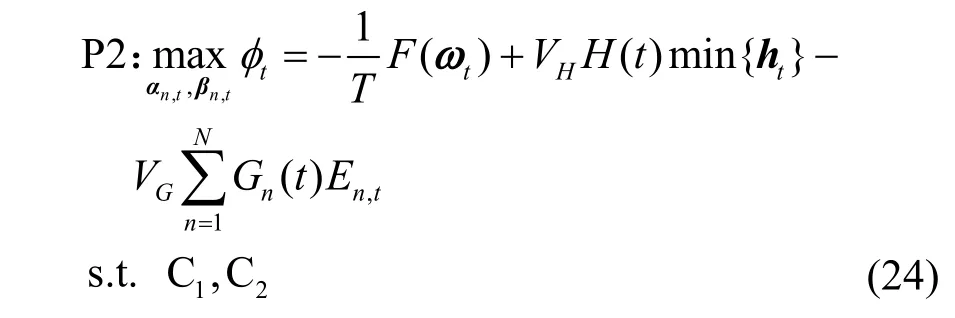
其中，VH和VG分别为对应调控信息新鲜度长期约束和终端能耗长期约束的权重。

进一步将转化后的问题P2 建模为MDP 优化问题，具体介绍如下。

1) 状态空间。定义终端能耗赤字集合为G(t)={G1(t),…,Gn(t),…,GN(t)}，终端能量预算集合为Emax={E1,max,…E2,max,…,EN,max}。状态空间表示为St=G(t) ⊗H(t)⊗Emax⊗hmin，其中⊗表示笛卡儿积。

2) 动作空间。动作空间定义为At={A1,t,…,An,t,…,AN,t}，其中An,t=αn,t⊗βn,t为终端n对应的动作空间。

3) 回报函数。回报函数定义为P2的优化目标，即φt。

2.2 电力至简物联网通信与计算资源协同优化算法

本文提出的算法可以求解2.1 节中构建的MDP优化问题，其核心思想是利用DQN 量化与拟合高维状态空间下的状态−动作价值，即表征动作累积奖励值的Q 值，并以此为依据优化信道分配与批量规模决策。本文算法结构如图3 所示，包括主网络、目标网络、经验池、多模态信道分配冲突解决模块、调控信息新鲜度赤字更新模块等。

图3 本文算法结构

IFAC3O 算法的执行主体为控制器。控制器基于终端Q 值比较解决多模态信道竞争冲突，其机理是将信道分配给能获得最大Q 值的终端，进而更有效地降低调控模型全局损失函数、调控信息新鲜度赤字与终端能耗赤字。IFAC3O 算法实现调控信息新鲜度感知和终端能耗感知的机理是在DQN的状态空间、回报函数值与Q 值中引入信息新鲜度感知和终端能耗性能赤字，使DQN 在基于性能偏差的迭代优化中能够不断拟合与感知动作价值与虚拟赤字队列演进之间的非线性复杂关联，并动态调整多模态信道分配与批量规模联合优化策略，实现通信与计算资源协同。

一次调控决策模型训练迭代可分为以下3 个步骤。首先，控制器基于主网络估计的Q 值优化信道分配和批量规模决策，并通过比较Q 值解决多模态信道分配冲突，其核心思想是将信道分配给能获得最大状态−动作价值的终端。其次，控制器下发信道分配和批量规模决策，所有终端执行本地模型训练和模型上传，并将能耗信息反馈至控制器。最后，基于终端上传的信息，控制器更新调控信息新鲜度赤字、终端能耗赤字，计算回报函数，更新经验池，并转移至下一状态。控制器计算DQN 损失函数，以此为依据更新主网络参数，并周期性更新目标网络参数。

IFAC3O 算法执行流程如算法1 所示，包括3个阶段，分别为初始化（步骤1)～步骤3)）、动作选择及多模态信道分配冲突解决（步骤5)～步骤16)）以及学习（步骤17)～步骤25)）。

初始化阶段。初始化Gn(t)=0，H(t)=0，αn,j,t=0，βn,t=0，∀n∈N，∀j∈J，∀t∈T。定义未被分配信道的终端集合为Nt，并初始化Nt=N。定义终端n∈Nt的可分配信道集合为Jn,t，并初始化Jn,t=J。

动作选择及多模态信道分配冲突解决阶段。首先，控制器基于ε-贪婪算法为每个终端选择动作。其次，当存在信道分配冲突时，例如同时为终端n和m分配信道j且控制器通过比较终端n和m的Q 值，将信道j分配给Q 值较大的终端n并拒绝终端m。随后，控制器将终端n移出未被分配信道的终端集合，即并设置被拒绝终端m的 Q 值为，其中，为终端m动作空间Am,t中对应于信道j的动作集合。基于更新的Q 值，重复上述动作选择及多模态信道分配冲突解决过程直到所有终端被分配信道。最后，控制器下发信道分配和批量规模决策，终端n∈N按照决策执行本地模型训练和本地模型上传，并将能耗信息En,t上传至控制器。

学习阶段。在学习阶段，控制器通过计算终端执行动作后的回报函数来更新DQN 参数，以提高DQN 对状态−动作价值的拟合精度，使DQN 输出最佳策略，实现信道分配和批量规模的优化，提高全局模型的精度，保障调控信息新鲜度，降低终端能耗。首先，基于终端上传的能耗信息，控制器根据式(19)更新终端能耗赤字Gn(t+1)。同时，控制器根据接收到的本地模型时间戳、模型下发时间以及式(10)、式(14)、式(15)计算获得第t次迭代的信息新鲜度，并根据式(20)更新调控信息新鲜度赤字H(t+1)。控制器根据式(24)计算回报函数φt。

其中，λ为折扣因子。

最后，基于υn更新主网络参数

其中，κ为学习步长。每T0次迭代更新目标网络为

本文所提IFAC3O 算法不需要专家经验，能够实现调控信息新鲜度感知和终端能耗感知，通过赤字虚拟队列演进感知每个时隙调控信息新鲜度与规定约束的偏差，并根据偏差自适应动态优化信道分配和批量规模，实现通信与计算资源的协同优化，从而提高电力至简物联网的资源编排管理水平和网络自治水平。具体而言，由式(20)可以看出，当调控信息新鲜度与规定约束偏离严重时，H(t)逐渐增加，导致回报函数值降低，迫使控制器调整信道分配和批量规模决策以降低调控信息年龄，提高调控信息新鲜度，保证控制器所接收本地终端模型的时效性，从而实现调控信息新鲜度感知，提高控制器分布式能源调控决策的准确性和可靠性。

3 仿真分析

3.1 仿真参数设置

本文通过对比不同的仿真算法来验证所提IFAC3O 算法的性能。考虑200 m×500 m 范围低压配电网，包含12 个部署于电力设备上的物联终端。本文应用MINST 数据集[24]验证所提IFAC3O 算法性能。MINST 数据集包含 6 ×104个训练样本，本文假设每个终端从中随机抽取50 个样本作为本地数据集Dn训练本地模型。DQN 采用四层神经网络结构，包含输入层、隐藏层1、隐藏层2和输出层，各层神经元数量分别为状态空间元素个数、128、128和动作空间元素个数。DQN 经验池大小设置为50。

具体参数设置如表1 所示[17,19]。对比算法设置为MDRL3RA 算法[12]和AFLBSO 算法[13]。其中，MDRL3RA 不具有能耗感知与调控信息新鲜度感知能力；AFLBSO 算法无法实现信道分配优化和解决信道分配冲突，不具有调控信息新鲜度感知能力。除此之外，文献[25]提出了一种最大干扰信道消除（MICD,maximum interference channel deletion）算法，通过优化信道分配，以最大化信息新鲜度。但是MICD 无法实现批量规模优化与能耗感知。

表1 仿真参数

3.2 仿真结果分析

图4 描述了全局损失函数随迭代次数的变化情况。随着迭代次数增加，全局损失函数先下降后稳定。当迭代次数为200 时，相比于MDRL3RA和AFLBSO，IFAC3O的全局损失函数分别降低了57.19%和24.60%。IFAC3O 在保障终端能耗与调控信息新鲜度长期约束的前提下，能够最大化参与本地模型训练的批量规模，从而降低全局损失函数。相关仿真结果在图5 中进一步阐述。

图4 全局损失函数随迭代次数变化情况

图5 平均调控信息新鲜度和平均批量规模对比

图5 对比了不同算法的平均调控信息新鲜度和平均批量规模。其中，平均调控信息新鲜度和平均批量规模分别定义为与MDRL3RA和AFLBSO 相比，IFAC3O的平均调控信息新鲜度分别提高了35.34%和49.05%，平均批量规模分别提高了31.72%和19.39%。针对计算能力较差的终端，IFAC3O 通过为其分配质量更好的信道降低了传输时延。针对等待时延较大的终端，IFAC3O通过增加其本地训练的批量规模，降低了等待时延，提高了调控信息新鲜度。

图6 描述了IFAC3O 算法训练时延、传输时延、等待时延和批量规模随迭代次数的变化情况。与第1 次迭代相比，IFAC3O 在经过199 次迭代后，批量规模增加了41.75%，训练时延增加了50.48%，传输时延下降了42.74%，等待时延下降了69.51%，总时延下降了24.64%。IFAC3O 调整了训练时延与等待时延占比，即通过优化信道分配降低传输时延，通过增加批量规模增大训练时延，从而使等待时延与总时延显著下降。

图6 IFAC3O 算法训练时延、传输时延、等待时延和批量规模随迭代次数的变化情况

图7 描述了传输时延随终端数量的变化情况。随着终端数量增加，信道分配冲突加剧导致传输时延逐渐增加，但IFAC3O 通过比较Q 值解决多模态信道分配冲突，其传输时延性能始终优于MDRL3RA和AFLBSO。虽然MDRL3RA 考虑了信道分配优化，但其无法解决信道分配冲突，因此其传输时延高于IFAC3O。当终端数量为15时，IFAC3O的传输时延比MDRL3RA和AFLBSO 分别降低了14.42%和23.11%。

图7 传输时延随终端数量的变化情况

图8 对比了不同算法200 次迭代终端能耗赤字与调控信息新鲜度赤字分布情况。由图8 仿真结果可以看出，IFAC3O 具有最低终端能耗赤字中位数与调控信息新鲜度赤字中位数。与MDRL3RA和AFLBSO 相比，IFAC3O的终端能耗赤字分别降低了20.07%和22.34%，调控信息新鲜度赤字分别降低了23.45%和26.77%。MDRL3RA和AFLBSO 无法保障调控信息新鲜度长期约束，导致调控信息新鲜度赤字波动范围较大。

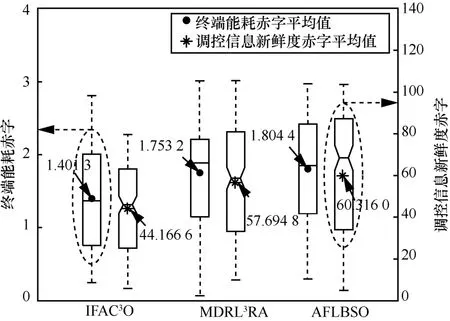
图8 不同算法200 次迭代终端能耗赤字与调控信息新鲜度赤字分布情况

图9 描述了平均调控信息新鲜度和平均信息年龄随调控信息新鲜度权重VH的变化情况。随着VH增大，平均信息年龄逐渐减小，平均调控信息新鲜度逐渐增加，同时等待时延显著下降。当VH从50增加至100 时，平均调控信息新鲜度提高了13.13%，平均信息年龄下降了24.72%，等待时延降低了32.09%。仿真结果表明，IFAC3O 主要通过减少等待时延降低信息年龄，进而提高调控信息新鲜度。

图9 平均调控信息新鲜度和平均信息年龄随调控信息新鲜度权重VH的变化情况

图10 显示了全局损失函数与平均调控信息新鲜度随迭代次数的变化情况。其中，柱状图表示全局损失函数的变化情况，折线图表示平均调控信息新鲜度的变化情况。由于MICD 通过不断迭代的方式在每次迭代中寻找最优信道分配结果，当迭代次数小于60 时，MICD的平均调控信息新鲜度高于IFAC3O。然而，IFAC3O 通过联合优化信道分配和批量规模，进一步提高了平均调控信息新鲜度。仿真结果表明，当迭代次数达到200 时，相较于MICD，IFAC3O的全局损失函数降低了39.22%，平均调控信息新鲜度提高了7.15%。

图10 全局损失函数与平均调控信息新鲜度随迭代次数的变化情况

本文通过MATLAB 验证所提IFAC3O 性能。表2 显示了IFAC3O 计算耗时随终端数量的变化，其中计算耗时定义为IFAC3O在MATLAB上单次执行所需要的时间。仿真结果表明，终端数量增多会导致DQN 输入状态和信道分配冲突概率增加，因此IFAC3O 耗时增长速度逐渐变大。由于仿真平台硬件配置限制，目前仿真计算耗时整体在秒级。当采用专用计算硬件模块，实际计算时延可以进一步降低至毫秒级甚至微秒级。

表2 IFAC3O 计算耗时随终端数量的变化

4 结束语

本文针对分布式能源调控决策模型损失函数最小化问题，提出基于调控信息新鲜度感知的电力至简物联网通信与计算资源协同优化算法，通过信道分配与批量规模的协同优化，在长期调控信息新鲜度约束下实现损失函数最小化。仿真结果表明，相较于MDRL3RA和AFLBSO，IFAC3O的全局损失函数分别降低了57.19%和24.60%，信息新鲜度分别提高了35.34%和49.05%，终端能耗波动分别降低了61.21%和11.80%。本文研究成果可运用于整县光伏、新型电力系统分布式能源并网工程中，为分布式能源调控模型训练提供信息新鲜度保障。在未来研究中，还需要进一步考虑多终端数据异构性对分布式能源调控模型训练的影响。