土工格栅加筋边坡最小势能稳定性分析方法
刘炜奇,温树杰,刘浚基,景彬余
(1.江西理工大学 土木与测绘工程学院,江西 赣州 341000;2. 江西理工大学 江西省环境岩土与工程灾害控制重点实验室,江西 赣州 341000)
1 概述
自然界中广泛地分布着许多自然边坡和人工边坡,作为一种最常见的工程地质环境,其稳定性分析已成为岩土界学者们关注的重点。为了避免边坡失稳的情况发生,对于一些安全系数较低的边坡,需对其进行加筋处理。土工格栅作为一种高强度结构材料,因具有抗拉强度高、延伸率低等特点而被选作为目前主流的边坡加固材料。
对于有加筋和无加筋边坡的稳定性分析,目前采用最广泛的方法仍是极限平衡法与有限元强度折减法[1-3]。LOW[4]等基于极限平衡原理,认为加筋的作用在于减小滑动体的力矩,将其等效于一个附加的抗滑力矩;WOODS[5]等基于LOW等人的研究,提出了加筋作用于不同的滑裂面时,其加筋效果会有差异,并推导了加筋边坡中临界滑裂面方程;介玉新[6]等基于有限元理论,提出将加筋土中的筋对土的力等效于附加应力作用与筋的方向上,只考虑土微元而忽略筋材微元,简化了分析。极限平衡法需划分条块、计算迭代并且作出一些限制滑动面的假设;有限元数值分析法作为目前岩土界运用最广泛的方法,该方法物理概念明确,适用性强,但由于加筋土中筋土作用关系复杂,很难确定模型参数与本构模型。目前每种方法仍存在一定的局限与不足之处,岩土界的学者们仍然在不断探寻着新的加筋边坡稳定性分析方法。
MAULDON[7]等基于能量的角度提出了最小势能法,近年来一些学者对最小势能法进行了完善和发展[8-11],但尚未有人开展最小势能法方面的土工格栅加筋边坡稳定性分析。因此笔者基于最小势能原理,提出了一种土工格栅加筋边坡的安全系数计算方法,该方法具有无需划分条块、无需迭代,计算简便等优点,便于在工程中运用。
2 滑体势能函数的构建
2.1 模型构建
边坡中的土工格栅布置见图1,边坡土体重度为γ,黏聚力为c,内摩擦角为φ。认为边坡的滑裂面形状可为任意形状,将其表示为y=f(x)。力学模型还需作如下假定:
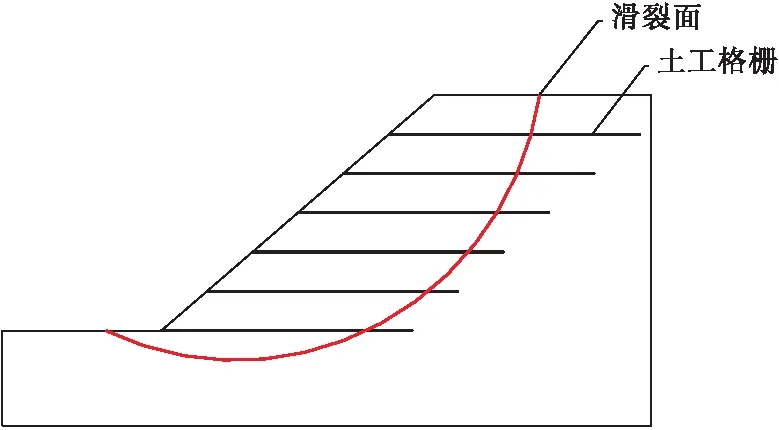
图1 土工格栅加筋边坡简图
a.将滑块视为刚体,用刚度为k的弹簧来模拟滑面上的弹性压缩变形。滑面上任意微段的长度为dl,且k与dl成正比,即k=mdl,其中m是地基系数。
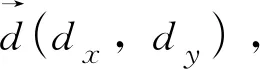
c.滑体发生微小位移时,整个系统因摩擦阻力的作用而储存了摩擦势能。
2.2 土工格栅势能的构建
土工格栅的势能包含了格栅摩擦势能和格栅弹性变形势能。
a.格栅摩擦势能的构建。
欲求得格栅的摩擦势能,须先求出土体与格栅的摩擦阻力。将格栅受摩擦阻力方向分为2种:一是朝滑块方向,二是朝滑床方向,如图2所示。

图2 摩擦阻力分布示意图
在滑体发生位移时,土工格栅发挥作用的部分只有埋置于滑床内的部分长度,将其称为有效长度,为了求解得到每层格栅的有效长度,建立如图3所示的坐标系。土工格栅水平埋设于边坡中,格栅编号从下到上依次是1,2,3,4,…,n。格栅垂直间距为hy。

图3 格栅有效长度计算简图
第i层土工格栅的y坐标可以表示为:
(1)
将式(1)与滑动面方程y=f(x)联立且取x>0时的情况,便可求出第i层土工格栅与滑动面的交点的x坐标xi,xi如式(2)所示:
xi=f-1(yi),x>0
(2)
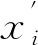
(3)
根据式(2)和式(3)可以求得第i层土工格栅的有效长度Li为:
(4)
通过式(4)求得格栅的有效长度Li,将其换算成有效表面积,即:
Si=2Liw
(5)
式中:Si为埋设于滑床内第i层土工格栅的部分表面积;w为土工格栅宽度。
由参考文献[12]可得知,第i层土工格栅的摩擦阻力Ti可由式(6)得到:
Ti=λ1λ2σiSif/nx
(6)
式中:σi为第i层土工格栅所受的上覆垂直应力;λ1是土工格栅面积影响系数;λ2是上覆压力的影响系数;nx为层间水平距离;f是摩擦系数。其中λ1,λ2,f为土工格栅相关参数,查阅资料获得。
通过式(6)计算所得格栅摩擦阻力并不一定为实际摩擦阻力,因为土工格栅拥有其极限抗拉力Tp,在边坡稳定性分析中,计算过程中格栅与土体间最大摩擦阻力不应超过其极限抗拉力。所以实际摩擦阻力应取二者较小值:
Tki=min(Ti,Tpi)
(7)
利用上述的推导,可以求得土工格栅的摩擦势能。由于摩擦阻力与位移夹角超过了直角,故其对系统做的功为负值,因此,摩擦势能Va为:
(8)

b.格栅弹性变形势能的构建。
推导格栅的弹性势能,格栅所受摩擦阻力Tki与自身纵向拉伸变形产生的拉力pi平衡,即pi=Tki。因此土工格栅弹性变形势能Vb为:
(9)

2.3 弹性压缩势能的构建
当滑面上发生弹性压缩变形时,在滑裂面上的微面可近似看作是刚度为k的弹簧,则微面上的弹性势能为:
(10)

(11)
上述推导得到了微面弹性势能为:
(12)
然后利用微面弹性势能对整个滑面积分,求得系统整体弹性势能为:
(13)
2.4 剪切势能的构建


图4 微单元受力分析图
根据微小单元受力平衡,可得:
Nicosα+τidlcosβ+Tkicosψ+
Ricosθ=0
(14)

由式(14)解得微面剪应力为:

(15)
当滑面处发生剪切变形时,参考文献[13]中关于微元剪切势能推导至系统剪切势能的推导公式,可得:
(16)
2.5 整个系统的势能
系统总势能由滑面上的弹性势能Vf、剪切势能Vτ和土工格栅摩擦、变形势能Va、Vb四者和减去外力R所做的功组成,即:
(17)
3 安全系数的求解
3.1 位移的求解
根据稳定平衡系统总势能最小的原理,有:
(18)
根据式(18)可解得虚位移dx、dy的值。
3.2 抗滑力的推导
将作用于滑体上的力中,与虚位移方向相反的力视为抗滑力。系统抗滑力包括:极限抗剪力提供的抗滑力dTd、法向力提供的抗滑力dNd、土工格栅提供的拉力pi(拉力pi的大小等于摩阻力Tki)。因此抗滑力分为以下3个部分:
a.剪切力提供的的抗滑力Td。
(19)
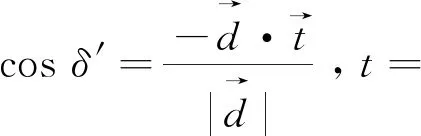

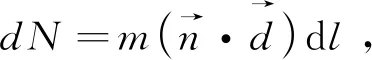
(20)

则法向力所能够提供的抗滑力为:
(21)

(22)
F抗滑力=Td+Nd+Pd=
(23)
3.3 下滑力的推导

(24)
3.4 安全系数的求解
(25)
通过上述的推导,我们可以发现安全系数的计算过程较为繁杂,为了方便工程运用,笔者利用matlab编写了一个针对上述安全系数的计算程序来辅助计算,程序界面如图5所示。

图5 程序界面
4 对比验证分析
边坡示意图见图6,该边坡为匀质边坡,且滑动面为圆弧形,其滑面方程为:
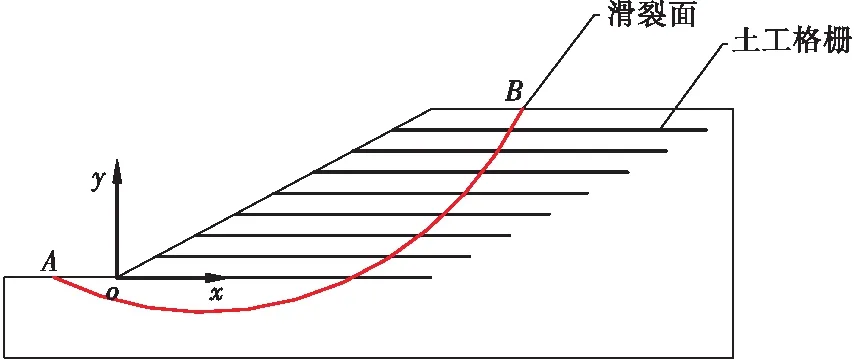
图6 加筋算例示意图
(x-5.2)2+(y-19.5)2=23.52
(26)
边坡参数为:坡高为14 m,斜率0.5,土体的重度γ=18.7 kN/m3。滑动面半径为23.5 m,内摩擦角φ=29°,黏聚力c=27.7 kPa。采用的土工格栅型号是PET25-25双向聚酯焊接土工格栅,设计埋设7层,间距为2 m,长度为16 m。具体物理力学参数可查阅规范。
上述算例通过文中方法计算得该边坡的安全系数是Fs=1.878,为了验证该安全系数的准确性和可靠性,用传统极限平衡法分析该边坡,并将其结果与本文结果进行对比,对比结果如下:本文方法1.878,瑞典条分法1.981,Janbu法1.924,Bishop法2.096。
本文方法计算结果与其他极限平衡方法的结果较为接近但偏安全。笔者考虑导致相差的主要原因为:①求解法向力时,传统极限平衡法通过划分条块,依据力的平衡原理求解法向力;而本文方法通过求解虚位移,利用力与位移的关系得到法向力的显式解,且整个过程无需划分条块,计算量小。②本文方法对安全系数的定义为抗滑力与下滑力的矢量和的比值,而且此过程无需迭代。
由于格栅尺寸和加筋层数的取值对边坡的安全系数有影响,为了分析格栅参数对边坡安全系数的影响规律,同时为了进一步验证文中方法的合理性,选定5组不同的格栅长度与加筋层数,利用文中方法分析其安全系数的变化,见图7、图8。当格栅长度为12 m时安全系数为1.838 9,14 m时为1.857 1,16 m时为1.878,18 m时为1.901 5,20 m时为1.927 7。当加筋层数为4层时安全系数为1.413,5层时为1.518 9,6层时为1.670 4,7层时为1.878,8层时为2.052 4。
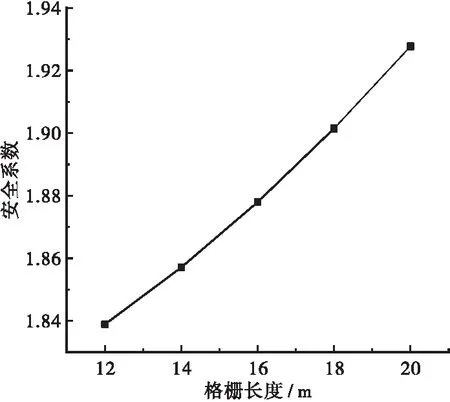
图7 不同格栅长度下的安全系数

图8 不同加筋层数下的安全系数
从图7可以看出:安全系数与格栅长度近似成正比关系,这是由于随着格栅长度的增加,其有效表面积随之增大,进而增大筋土摩擦阻力,提高安全系数。由图8可以看出:安全系数同时也随着加筋层数的增大近似成正比,且加筋层数的改变对安全系数带来的影响大于格栅长度的改变。上述安全系数随格栅长度与加筋层数变化的规律特点与文献[14-15]中的研究结果是一致的。
5 结论与建议
文中分析方法是建立于最小势能原理上的,安全系数的求解方式异于传统极限平衡法。通过对同一边坡算例进行验证与分析,得到的主要结论为:
a.通过推导土工格栅的摩擦和变形势能,建立了加筋边坡的系统势能函数,并且基于最小势能原理提出了一种土工格栅加筋边坡的稳定性分析方法。与算例对比验证了文中方法的合理性,且文中方法无需划分条块和无需迭代,相较于传统极限平衡法具有一定的优势。
b.加筋边坡安全系数与格栅长度和加筋层数近似呈正比关系,格栅长度的改变对安全系数影响较小,而格栅层数的改变对安全系数的影响较大。
c.笔者仅推导了任意形状滑裂面的加筋边坡安全系数计算方法,对于加筋边坡滑裂面的构造和临界滑裂面的搜索,还需进行更深入的研究。

