大跨度悬臂浇筑钢筋混凝土拱桥多目标索力优化研究
曹检云,刘国坤,孙剑峰
(1.长沙市规划设计院有限责任公司,湖南 长沙 410007;2.湖南省交通科学研究院有限公司,湖南 长沙 410015)
0 引言
随着我国交通基础设施在内陆山区的不断建设,钢筋混凝土拱桥以其跨越能力大、受力条件合理、一体性强和对河流通航能力影响较小等特点成为了众多桥型方案中的优选方案[1]。与普通跨高山峡谷钢筋混凝土拱桥不同,跨水库区钢筋混凝土拱桥由于受库区蓄水的影响,环境条件更为复杂,水库对地应力场的重分布作用会改变桥梁结构的动力特性[2],因此需要对库区钢筋混凝土拱桥进行优化设计,使其受力达到最佳状态具有必要性。
跨库区钢筋混凝土拱桥一般采用悬臂浇筑的施工方案,与斜拉桥悬臂浇筑施工不同,钢筋混凝土拱桥悬浇施工过程中的扣索力大小对拱圈结构的内力和线形影响都更为显著,基于此,众多学者对大跨度悬浇拱桥的扣索力优化展开了深入研究。孙波[3]等基于模拟退火算法对某悬浇钢筋混凝土拱桥进行了索力优化,有效降低了扣塔高应力区的应力集中现象,保证了施工安全;刘增武[4]等采用“未知荷载系数法”获取了算例的最大悬臂状态索力初值,通过正装分析对扣索力展开了优化,确保施工过程中的拱圈截面拉应力满足设计值要求;熊兴兵[5]等利用Matlab求解了索力、临时预应力和拱圈应力间的影响系数,并采用线性规划理论实现了对扣索力的重分配,达到了对扣塔应力的合理调整;何畏[6]等建立了新密地大桥的ANSYS参数化模型,并采用ANSYS一阶优化的方法分施工阶段和成桥阶段对扣索力进行了优化研究,实现了拱桥在施工阶段和运营阶段的合理受力。
以上研究多以单一目标对悬浇钢筋混凝土拱桥进行索力优化,输出的索力组合往往存在一定的局限性,本文基于多目标优化的思想,以各拱圈节段顶底板拉应力峰值、主拱恒载下的内力分布和松索后的拱桥线形为目标函数,联合ANSYS参数化模型,采用改进后的多目标粒子群优化算法对库区大跨度钢筋混凝土拱桥实现了索力优化,并验证了输出的最优索力组合对拱桥内力分布与变形状态的改善,可为今后类似的工程提供一定参考。
1 工程概况
本文以某跨水库区大跨度悬臂浇筑钢筋混凝土拱桥为工程背景,主桥拱圈为等高悬链线钢筋混凝土箱型梁结构,跨径240 m,净高40 m,拱轴系数m=1.85。拱圈采用悬臂浇筑工艺建造,截面为单箱双室,基本截面数据如下:宽×高为(10×4.5)m,拱脚底板厚0.8 m、腹板厚0.65 m,L/4截面顶板厚0.35 m、腹板厚0.4 m,拱顶L/2截面顶板厚0.5 m、腹板厚0.5 m、底板厚0.35 m。拱圈沿纵向分为37个节段,包括34个斜拉扣挂挂篮悬浇段和1个吊架现浇合龙段。拱圈悬浇节段达到设计强度后,利用扣索进行锚固,临时扣塔采用Q345a钢材,扣索采用预应力钢绞线,扣锚索施工布置图如图1所示。
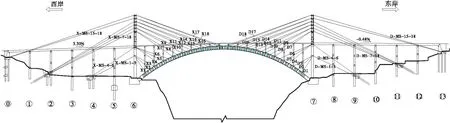
图1 扣锚索施工布置图
2 基于多目标的索力优化模型建立
2.1 ANSYS有限元模型
为实现对拱桥施工阶段和成桥阶段的索力模拟和内力调优,编写ANSYSAPDL命令流建立全桥的参数化有限元模型。采用Solid65八节点三维混凝土实体单元模拟混凝土主拱圈和交界墩;Beam188梁单元模拟钢结构扣塔;Link10自建单元模拟扣、锚索。利用ELIVE命令和EKILL命令模拟主拱圈实际的施工阶段,首先使用EKILL命令“杀死”所有单元,从第一节段拱圈施工开始,使用ELIVE命令逐渐激活各施工阶段实际浇筑完成的拱圈节段单元,由于拱圈采用实体单元进行模拟,无法通过施加节点荷载的方式模拟各拱圈节段所受的自重和挂篮荷载,本文采取在每个浇筑阶段设置MASS21质量节点的方式进行施工荷载的模拟。考虑计算结果精度的要求,采用映射分网技术对ANSYS模型进行网格划分,混凝土拱圈实体单元使用六面扫略分网,建立ANSYS有限元模型如图2所示。
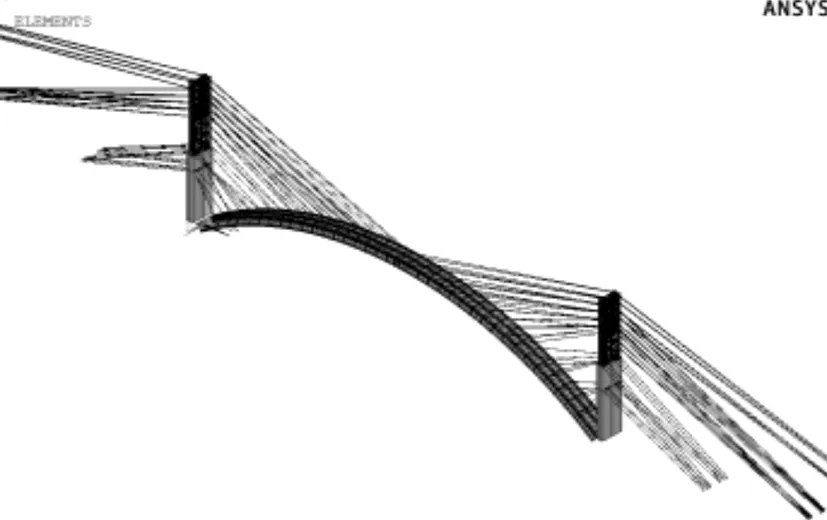
图2 ANSYS有限元模型
2.2 多目标索力优化数学模型建立
大跨度悬浇钢筋混凝土拱桥施工阶段合理索力的确定,既需要考虑施工阶段扣索体系与悬臂拱圈相互耦合的受力安全,又需要保证成桥后的拱圈结构应力分布满足要求,还需要满足变形控制条件,本文引入多目标优化的基本思想对合理索力进行寻优,设置的优化控制目标如下:
对于悬臂浇筑施工阶段,混凝土拱圈顶板与底板拉压应力交替转化,处于复合受力状态,由于混凝土抗拉强度较低,为防止扣索张拉过程中因拉应力超标而引起的顶底板裂缝,需要对扣索索力进行控制,保证拱圈截面的拉应力处于安全界限内。以各施工阶段拱圈控制截面上顶、底部拉应力之和的平均值作为施工阶段为控制指标,建立拱桥索力优化的第1目标函数,如式(1)所示:
(1)
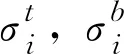
在混凝土拱桥主跨拱圈合龙前对扣索索力进行重调可以有效改善成桥后的内力分布,降低由恒载产生的弯矩。选择主拱偏心矩作为混凝土拱桥成桥内力的控制指标,建立拱桥索力优化的第2目标函数,如式(2)所示:
(2)
式中:ei为优化后成桥恒载状态下的偏心矩,ei=Mi/Ni,其中,Mi和Ni分别为优化后成桥恒载状态下的弯矩和轴力。
考虑悬浇施工阶段扣索力对拱圈结构线形的影响,选取松索后各拱圈节段控制截面的设计竖向位移和计算竖向位移差的平方和为变形控制指标,建立拱桥索力优化的第3目标函数,如式(3)所示:
(3)
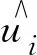
综上所述,基于多目标优化思想建立大跨度悬浇钢筋混凝土拱桥的索力优化模型,选取扣索索力作为设计变量,数学模型如式(4)所示:
Min(Obj1,Obj2,Obj3)=
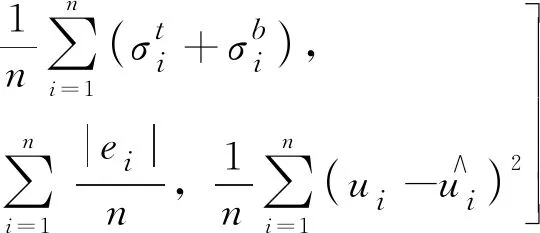
(4)
xi,min≤xi≤xi,max,i=1,2,…,n
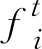
3 多目标粒子群算法寻优模型
3.1 改进的多目标粒子群优化算法
多目标粒子群优化算法(MOPSO)以粒子群优化算法(PSO)为基础,由于多目标优化问题的特殊性,当出现非支配解集时,无法对个体极值和全局极值进行准确定义和更新,因此MOPSO在进行多目标寻优时需要通过构造外部集的方式保存种群从寻优开始的所有非支配解,并采取引导非支配解的方式迅速接近Pareto最优前沿。
为适应大跨度悬浇拱桥索力优化模型的求解特性,实现施工阶段和成桥阶段的优化目标,同时确保算法不陷入局部最优解集,本文对MOPSO采取构建外部冗余集的改进策略精简寻优过程,保证Pareto最优前沿的分布性能 ̄[7]。具体改进方式如下:
对外部集A中的粒子排序后随机选择,再进行变异操作,构建冗余集R,变异过程如式(5)、式(6)所示:
(5)
(6)
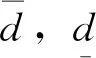
定义种群速度V作为种群扰动的判断条件,当种群速度V小于初始速度限制时,在冗余集R中随机选择一定规模的粒子迁入种群,替换同等规模适应度最差的粒子;当种群速度V大于初始速度限制时,更新外部集并清空冗余集。种群速度V如式(7)所示:
(7)
式中:D为目标空间的维数;N为决策变量的维数;vi为解集中粒子的速度。
采用构建外部冗余集的方式改进MOPSO算法对本文悬浇拱桥索力优化模型的求解有如下2个作用:①对种群形成干扰,防止以全局最优粒子为搜索中心的寻优方式导致算法出现“早熟”或陷入单一目标最优解的情况;②精简寻优过程,随着迭代次数的增加,多目标优化问题会出现规模巨大的外部非支配解集,对外部集进行排序并清空一定比例适应度差的粒子可以大大减少ANSYS模型计算量,达到快速寻优的效果。
3.2 优化模型求解步骤
采用MATLAB编写多目标索力优化程序,与ANSYS进行联合求解,优化流程如图3所示,优化步骤如下:
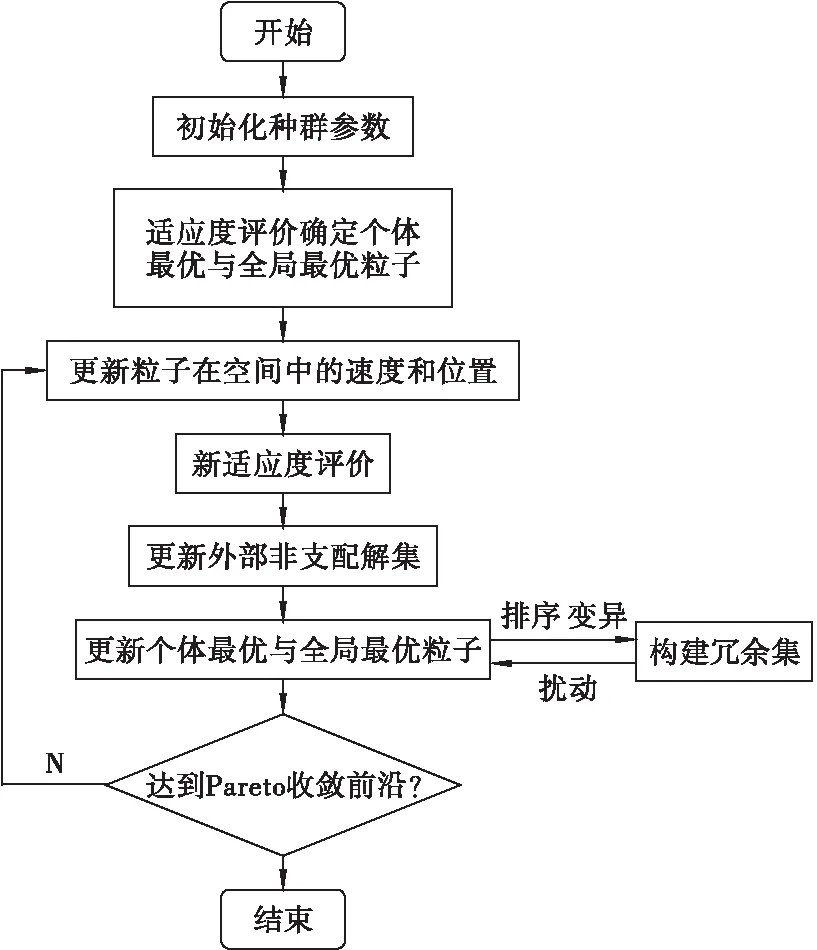
图3 多目标粒子群算法索力优化流程
步骤1:初始化粒子群种群参数。本文粒子群个体数量为20,Pareto最优解集数量为50,迭代次数为50次。
步骤2:适应度评价。将粒子群描述的索力值x代入ANSYS模型进行求解,返回Obj1,Obj2,Obj3目标函数值作为适应度评价指标,确定当前迭代轮次的个体最优与全局最优粒子。
步骤3:通过学习函数更新粒子群在空间中的速度和位置,确定更新前后粒子的支配关系,保留非支配外部解集。
步骤4:对外部集进行排序后随机选择一定规模的粒子进行变异操作,构建冗余集,根据种群扰动条件判断是否扰动,替换同等规模适应度最差的粒子后更新外部集。
步骤5:更新个体最优与全局最优粒子,并判断是否达到Pareto收敛前沿,若达到则终止迭代,反编译得到索力优化值并代入ANSYS模型进行正装计算,若未达到则返回步骤2进入新的迭代轮次。
3.3 Pareto最优解集
本文以大跨度悬浇拱桥施工阶段顶底板拉应力峰值Obj1、成桥阶段拱圈内力分布Obj2和拱圈位移控制Obj3为多目标进行优化,对迭代过程中的Pareto最优解集前沿分布进行分析,图4给出了多目标粒子群优化算法执行过程中的Pareto前沿分布情况。由图可知,本文优化模型的Pareto前沿呈三维空间曲面分布,且Pareto前沿随着各轮迭代不断向Obj1、Obj2和Obj3的最小值逼近,并于第50轮迭代基本收敛至极值附近。
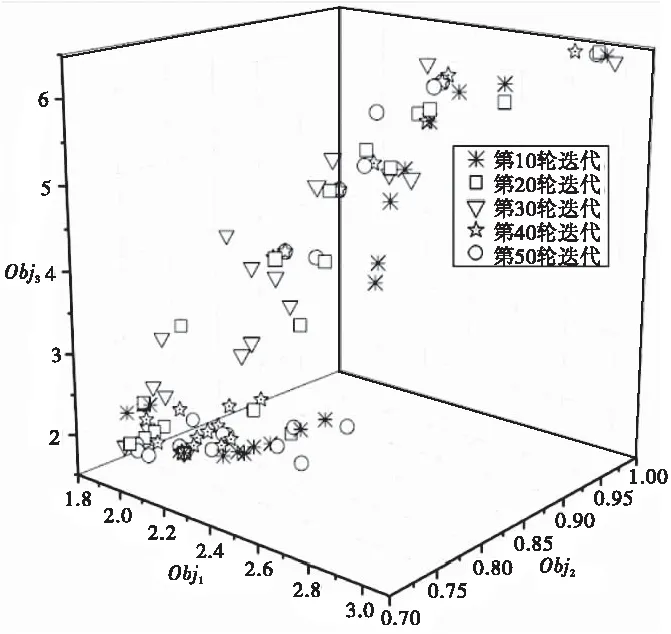
图4 Pareto 前沿分布
4 优化结果分析
基于东西两岸悬浇工程的对称性,本文以西岸18根扣索为例对索力优化结果进行分析。图5给出了西岸18根扣索索力优化前后的对比图,由图可知,原设计方案中扣索索力初值较为保守,在改进的多目标粒子群算法优化后,各扣索力均有不同程度的增幅。优化后的索力分布与原设计方案基本保持一致趋势,即拱顶、拱脚处索力较小,拱腰处索力较大,其中拱脚至拱腰段扣索力优化后平均增幅较小,约为10%左右,拱腰至拱顶段扣索力优化后平均增幅较大,约为20%左右。分析原因可知,随着拱圈悬浇过程的进行,扣索与拱圈节段的夹角不断减小,扣索提供的索力在垂直于拱圈节段方向越来越小,平行于拱圈节段方向越来越大,因此优化后的扣索力在拱腰至拱顶段可以提供更大的垂直分量,保证悬浇扣挂体系的稳定性。
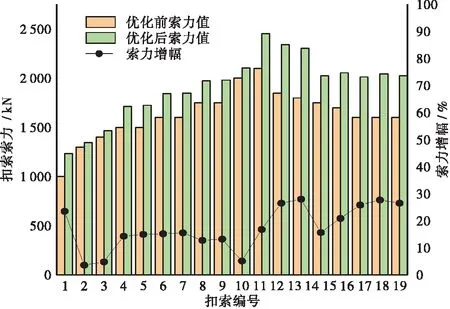
图5 优化前后索力值对比
图6分别给出了索力优化前后各拱圈节段顶、底板峰值拉应力的对比图。由图可知,索力重调后,拱圈顶、底板拉应力峰值均大幅度下降,拱腰处各拱圈拉应力峰值降幅最大,均为50%左右,拱顶处各拱圈节段拉应力峰值降幅最小,均为10%左右,优化后的拉应力峰值均小于C60混凝土抗拉强度设计值,且留有一定富余,达到优化目的。
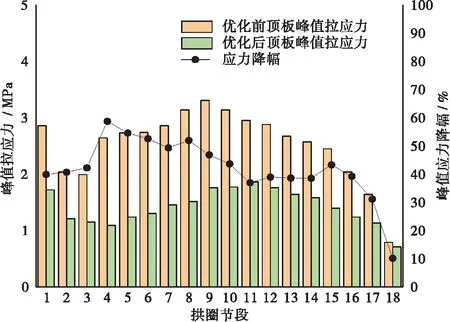
(a) 顶板峰值拉应力
表1给出了优化前后成桥状态下拱脚与拱顶的弯矩值。由表可知,索力重调后,拱脚弯矩由83 373.53 kN·m降低至69 487.67 kN·m,降幅为16.7%;拱顶弯矩由9 543.24 kN·m降低至6 421.43 kN,降幅为22.2%,可见对索力重调后,恒载作用下主梁内力分布更加合理,峰值弯矩均得到一定程度的减小,拱腰部分弯矩分布更加均匀,达到优化目的。
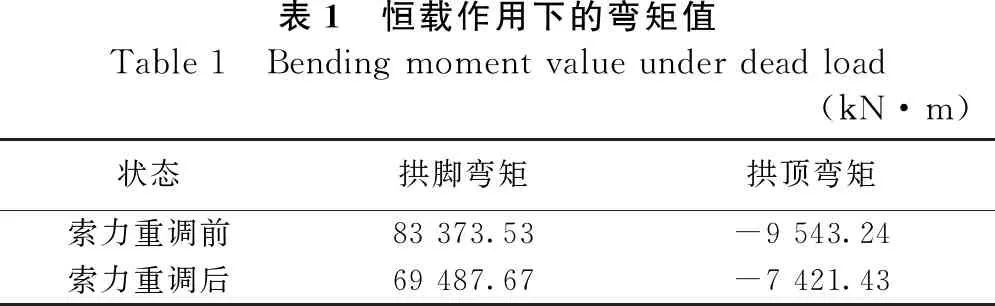
表1 恒载作用下的弯矩值Table 1 Bending moment value under dead load(kN·m)状态拱脚弯矩拱顶弯矩索力重调前83 373.53-9 543.24索力重调后69 487.67-7 421.43
图7给出了拱圈松索后各节段悬臂端竖向位移曲线。由图可知,拱脚处拱圈悬臂端竖向位移较小,拱顶处较大,松索后拱圈线形良好。随着扣索长度的增加,从东西两岸第9节段开始,扣索平均索力逐渐增大,合龙段扣索水平倾角减至最小,达到下挠峰值。索力优化后拱圈的线性基本保持与优化前一致,拱腰至拱顶段竖向位移均有不同幅度的降低,拱圈整体变形受到一定程度的控制,达到优化目的。
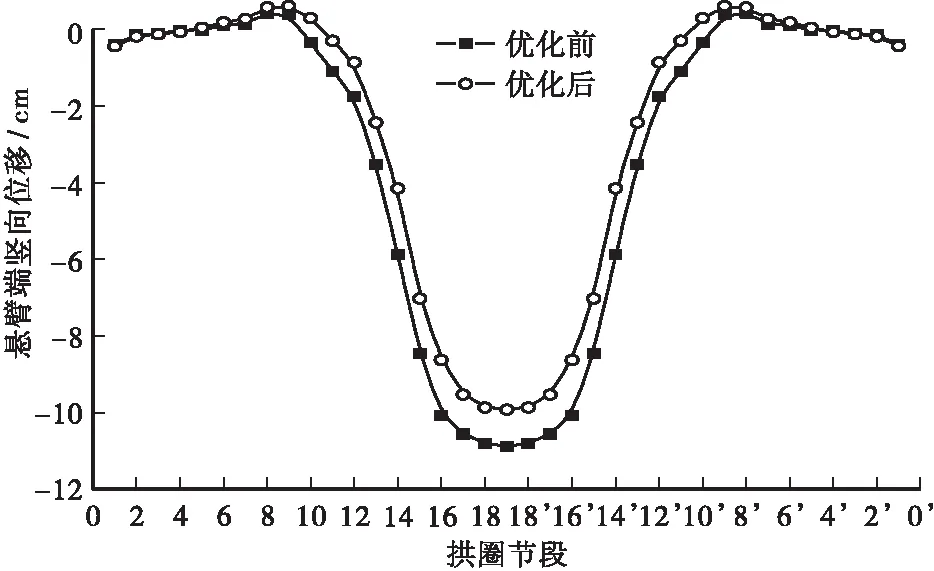
图7 拱圈各节段竖向位移
5 结论
本文以某水库区大跨度悬浇钢筋混凝土拱桥为工程背景,基于多目标优化理论与改进的粒子群优化算法,联合ANSYS有限元模型对拱桥扣索力进行了全局寻优,达到了对拱圈顶底板拉应力、成桥内力分布和松索后变形控制的优化目标,得到结论如下:
a.库区大跨度悬臂浇筑钢筋混凝土拱桥可以基于多目标优化思想建立数学优化模型,同时达到对施工阶段和成桥阶段的控制目标。
b.改进的多目标粒子群算法在保证寻优精度的前提下大幅度降低了计算量,提高了粒子群的寻优速度。冗余集的构建减少了大量非最优索力解的输出,且由于变异粒子对适应度差粒子的等规模替换,改进多目标粒子群算法可以防止输出的索力组合陷入某个目标函数的局部最优解,迅速到达Pareto收敛前沿。
c.由优化结果可知本文工程中扣索力设计初值偏于保守,留有较大安全富余度,优化后不同扣索的索力均有一定幅度的提升,充分利用了扣索的抗拉承载力。基于多目标粒子群优化算法重调的索力组合使各拱圈顶底板峰值拉应力得到大幅度改善,拱腰处部分节段拉应力峰值降幅最大达50%左右;成桥恒载作用下,拱顶负弯矩与拱脚正弯矩均有20%左右的降低,主拱内力分布更加均匀合理;松索后的拱圈线形基本保持与优化前一致,拱腰至拱顶段的竖向位移幅值均有一定程度的降低。

