混凝土键齿胶接缝承载力计算方法研究

丰锦铭,王祺顺,刘国坤

(湖南省交通科学研究院有限公司，湖南 长沙 410015)

1 概述

随着装配式结构和快速化施工技术的蓬勃发展，节段预制拼装混凝土桥梁开始广泛应用于公路桥梁、铁路桥梁和城市高架桥等各种桥梁工程。标准化生产的预制拼装节段不仅可以达到桥梁快速化施工的要求，而且具有经济性好、安全、交通干扰小、环境污染少、施工周期短等优点。节段桥梁内的纵向钢筋在键齿接缝截面截断，采用预应力钢束把各个分离的预制节段连接为一个整体。接缝具有复杂的受力特征，同时作为不连续的薄弱位置，其受力性能是节段桥梁结构性能的一个关键问题[1]。

目前，常见接缝构造有干、湿和胶接缝3种处理方式。干接缝施工过程最为简单，无须额外接缝处理，其缺点则是接缝表面局部缺陷可能会影响结构拼装精度，另外在接缝位置预应力筋受腐蚀可能性较高，会影响结构耐久性。湿接缝则是通过现场浇筑接缝位置混凝土来将结构连接起来，其缺点就是施工周期长，与快速化预制拼装理念冲突。胶接缝一般是通过环氧树脂将节段间连接起来，有利于结构拼装精度，且接缝处有环氧树脂填充，不会使体内预应力钢筋暴露在外，耐久性相对较好。因此，胶接缝在3种接缝处理方式中应用较多且性能更好，因此本文以此为对象展开混凝土键齿胶接缝研究。

国内外多所高校的学者对节段预制拼装桥梁键齿胶接缝的受力性能展开过研究，完成了大量的试验加载和理论分析。1983年，KOSEKI和BREEN[2]对接缝的抗剪性能进行了较为系统的研究，分别完成了平接、单键齿和多键齿干/胶接缝的试验研究，结果发现胶接缝的破坏主要表现为混凝土的压碎，而且胶接缝抗剪强度接近于整体浇筑试件。1989年到1991年之间，BAKHOUM[3]完成了一大批混凝土接缝的直剪试验，研究发现环氧树脂胶接缝的直接剪切承载力要高于干接缝，然而胶接缝试件表现为更为突然且明显的脆性失效，侧向应力的增大会增加接缝的承载力，但是对接缝试件的刚度影响很小；接缝处施加的胶层厚度大小对接缝的抗剪承载力影响不大，但是厚度增大会使接缝刚度降低。2002年，ROMBACH[4]对节段梁预制拼装技术的构造和制作方法等进行了全面总结，并给出与传统AASHTO规范公式不同的干、胶接缝的承载力计算公式，ROMBACH对接触面摩擦的贡献考虑是采用全截面面积而非摩擦接触面面积计算。2004年，卢文良[5]综合已有试验资料提出胶接缝试件破坏基本是全截面剪切破坏，而且多键齿试件键齿几乎同时剪切失效，对多键齿试件引入多键不均匀性降低系数，从而给出了不同接缝类型的抗剪强度计算公式。之后，东南大学刘钊[6]、宋守坛[7]、王建超[8]对常规混凝土接缝直剪性能进行了一系列试验研究，并各自考虑不同影响因素给出了一些接缝的抗剪强度计算公式。袁爱民[9]等完成了多个胶键齿直剪试验，对剪力键的键齿宽高比与宽间比进行研究，发现试件荷载滑移曲线无明显的稳定屈服段，整个加载过程可以描述为弹性与错动滑移2个阶段，错动滑移持续增加，构件发生脆性破坏。

综上可知，目前已开展的针对节段预制桥梁胶接缝的直接剪切试验较多，但是针对已有试验研究和计算公式的总结分析较少。因此本文收集国内外试验数据和计算公式，进一步分析总结了4种键齿胶接缝的直剪计算模型，拟合得到了4个计算公式。同时对已有公式和本文公式基于试验结果进行了适用性和准确性评价。本文公式可以为完善节段桥梁键齿胶接缝的设计、计算提供参考。

2 试验研究与数据

2.1 典型试验方法

针对键齿胶接缝的直接剪切性能，国内外学者进行了大量的接缝加载试验[2-10]。其中推出试验作为典型的试验方法被广泛应用，而推出试验采用的试件主要分为2种，如图1所示。Z字形键齿则由一阴一阳2个键齿组成，直接在接缝的正上方加载，相对而言，采用Z字形试件的研究更多；ABA试件由2个阴键齿夹住中间的阳键组成，在阳键齿中上部加载，左右两个键齿可以互相对照。然而，这2种试验方法都难以实现完全的直接剪切状态，具有一定的局限性。

(a)Z字形试件

2.2 试验数据库

已有研究表明：混凝土强度、键齿、接缝面积、侧向应力大小、胶层厚度和侧向刚度等因素均会对键齿胶接缝的抗剪性能产生影响。其中，最重要的影响因素主要包括键齿尺寸、接缝面积、侧向应力和混凝土强度，其他因素影响较小，本文不予考虑。表1给出了国内外一共53组试验参数。

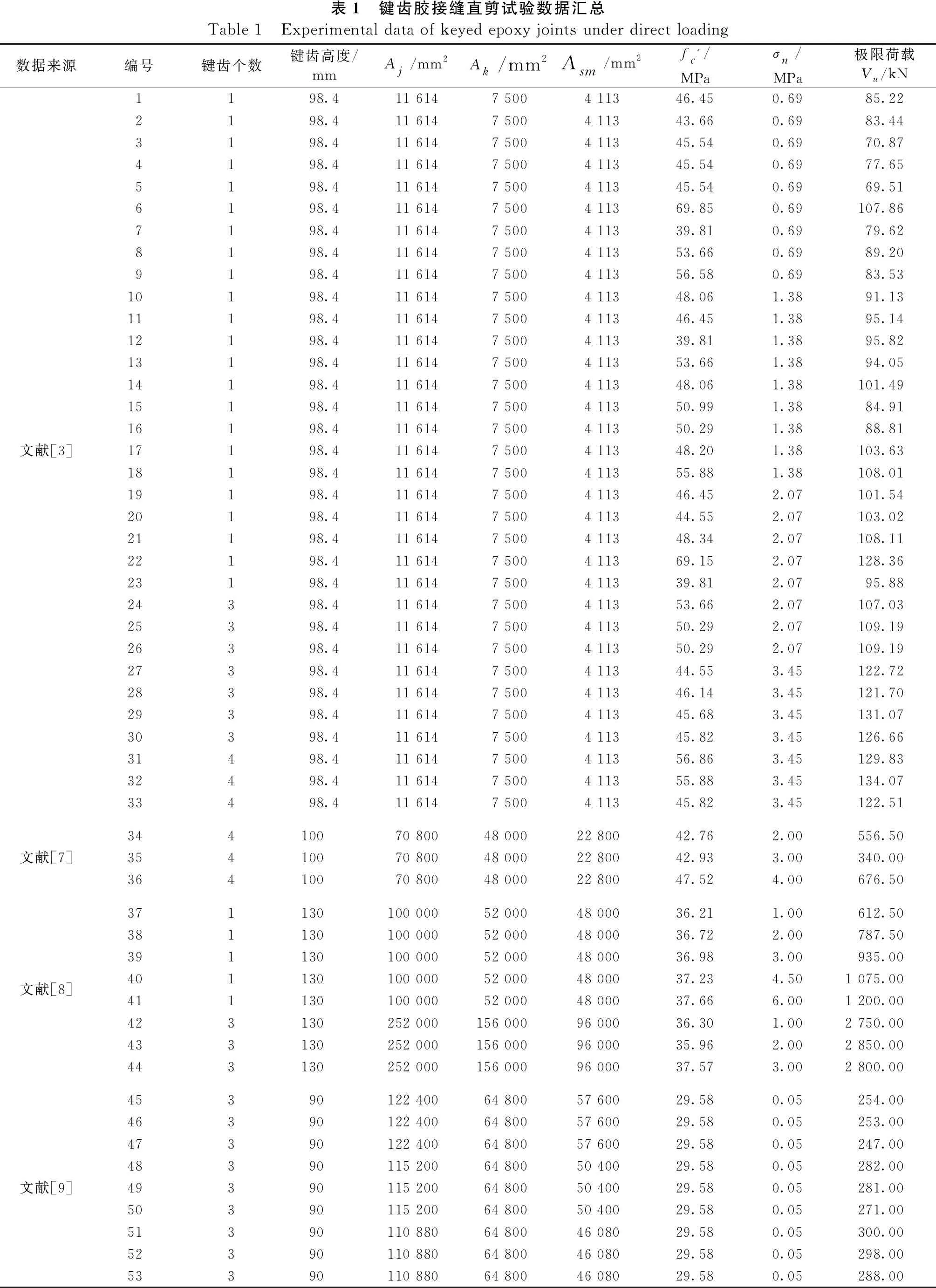
表1 键齿胶接缝直剪试验数据汇总Table 1 Experimental data of keyed epoxy joints under direct loading数据来源编号键齿个数键齿高度/mmAj/mm2Ak/mm2Asm/mm2fc'/MPaσn/MPa极限荷载Vu/kN1198.411 6147 5004 11346.450.6985.222198.411 6147 5004 11343.660.6983.443198.411 6147 5004 11345.540.6970.874198.411 6147 5004 11345.540.6977.655198.411 6147 5004 11345.540.6969.516198.411 6147 5004 11369.850.69107.867198.411 6147 5004 11339.810.6979.628198.411 6147 5004 11353.660.6989.209198.411 6147 5004 11356.580.6983.5310198.411 6147 5004 11348.061.3891.1311198.411 6147 5004 11346.451.3895.1412198.411 6147 5004 11339.811.3895.8213198.411 6147 5004 11353.661.3894.0514198.411 6147 5004 11348.061.38101.4915198.411 6147 5004 11350.991.3884.9116198.411 6147 5004 11350.291.3888.81文献[3]17198.411 6147 5004 11348.201.38103.6318198.411 6147 5004 11355.881.38108.0119198.411 6147 5004 11346.452.07101.5420198.411 6147 5004 11344.552.07103.0221198.411 6147 5004 11348.342.07108.1122198.411 6147 5004 11369.152.07128.3623198.411 6147 5004 11339.812.0795.8824398.411 6147 5004 11353.662.07107.0325398.411 6147 5004 11350.292.07109.1926398.411 6147 5004 11350.292.07109.1927398.411 6147 5004 11344.553.45122.7228398.411 6147 5004 11346.143.45121.7029398.411 6147 5004 11345.683.45131.0730398.411 6147 5004 11345.823.45126.6631498.411 6147 5004 11356.863.45129.8332498.411 6147 5004 11355.883.45134.0733498.411 6147 5004 11345.823.45122.5134410070 80048 00022 80042.762.00556.50文献[7]35410070 80048 00022 80042.933.00340.0036410070 80048 00022 80047.524.00676.50371130100 00052 00048 00036.21 1.00612.50 381130100 00052 00048 00036.72 2.00787.50 391130100 00052 00048 00036.98 3.00935.00 文献[8]401130100 00052 00048 00037.23 4.501 075.00 411130100 00052 00048 00037.66 6.001 200.00 423130252 000156 00096 00036.30 1.002 750.00 433130252 000156 00096 00035.96 2.002 850.00 443130252 000156 00096 00037.57 3.002 800.00 45390122 40064 80057 60029.580.05254.00 46390122 40064 80057 60029.580.05253.00 47390122 40064 80057 60029.580.05247.00 48390115 20064 80050 40029.580.05282.00 文献[9]49390115 20064 80050 40029.580.05281.00 50390115 20064 80050 40029.580.05271.00 51390110 88064 80046 08029.580.05300.00 52390110 88064 80046 08029.580.05298.00 53390110 88064 80046 08029.580.05288.00

3 胶接缝承载力计算公式

3.1 美国AASHTO节段桥梁设计规范

美国AASHTO节段桥梁设计规范(1989)[11]中给出键齿胶接缝的抗剪承载力计算公式如下：

Vj=Aj(4.17+1.06σn)

(1)

式中:Aj为接缝面总面积；σn为侧向应力。

3.2 Bakhoum公式

1991年，Bakhoum[3]通过试验研究和理论分析，给出键齿胶接缝的抗剪强度公式如下：

(2)

式中:fc'是混凝土圆柱体抗压强度；其余参数含义同上。

3.3 Rombach and Specker公式

2002年，Rombach[4]通过试验研究和理论推导得到键齿胶接缝的直剪承载力计算公式如下：

Vj=0.14fckAk+μAjσn

(3)

式中:Ak为胶接缝键齿根部面积；μ为摩擦系数，取0.65；fck为混凝土抗压强度标准值；其余参数意义同上。

3.4 卢文良公式

21世纪后，我国学者逐渐展开对节段桥梁的研究，卢文良[5]提出键齿胶接缝的抗剪承载力计算公式如下：

(4)

式中：参数意义同上。

3.5 刘钊公式

刘钊[6]将键齿胶接缝承载力由混凝土立方体抗压强度表示，具体形式如下：

(5)

式中:α为键齿接缝折减系数，取0.85～0.9，本文计算时取0.85；fcu，k为混凝土立方体抗压强度；其余参数意义同上。

3.6 王建超公式

王建超[8]在计算公式中考虑了键齿数和应力梯度的影响，公式如下：

(6)

式中:ν为开裂混凝土抗压强度软化系数，建议取0.6；其余参数意义同上。

3.7 宋守坛公式

宋守坛[7]在计算公式中引入来了键齿高度修正系数，公式表示如下：

(7)

(8)

式中:ζ为键齿高度修正系数；Asm为接缝面摩擦面积；H为键齿高度；其余参数意义同上。

3.8 袁爱民公式

河海大学袁爱民[12]提出键齿胶接缝承载力计算如下：

(9)

式中:各参数意义同上。

4 胶接缝承载力计算公式分析

4.1 计算结果对比

本节根据国内外学者所提出的上述计算公式和本文所收集的试验数据，首先计算得到各个试件的抗剪承载力，进而得到试验值与理论值的比值，同时对计算结果加以分析，结果对比见表2。另外各公式预测值与试验数据的关系见图2。

(a)AASHTO

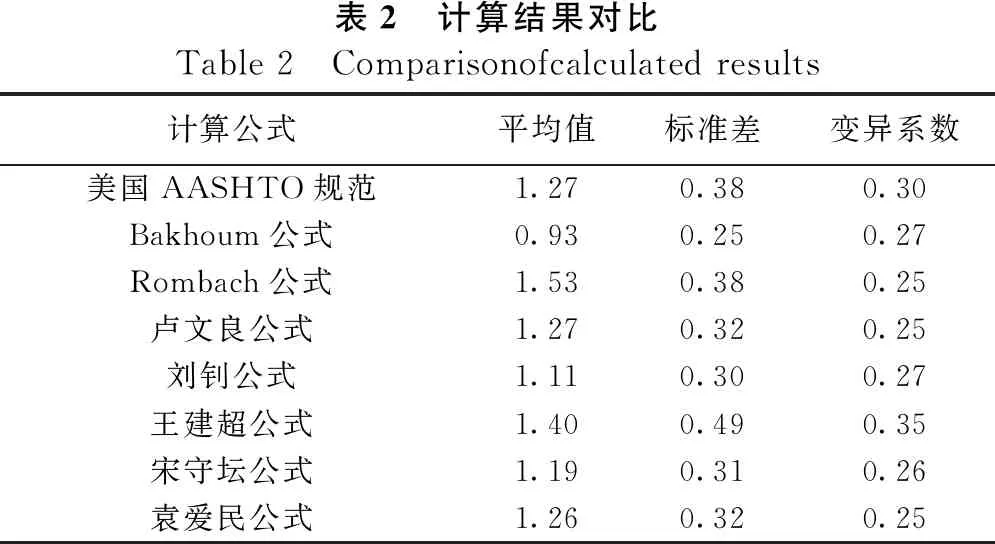
表2 计算结果对比Table 2 Comparisonofcalculated results计算公式平均值标准差变异系数美国AASHTO规范1.270.380.30Bakhoum公式0.930.250.27Rombach公式1.530.380.25卢文良公式1.270.320.25刘钊公式1.110.300.27王建超公式1.400.490.35宋守坛公式1.190.310.26袁爱民公式1.260.320.25

从表2可知：除了试验值与Bakhoum公式的预测值的比值小于1，偏不安全外，试验结果与其余公式的预测值的比值都大于1，可以保证计算结果的安全性；试验值与Rombach公式的比值达到1.53，结果最为保守；其他公式中要属Bakhoum预测的抗剪承载力最为准确，平均值达到0.93；其次是Rombach、卢文良和袁爱民公式预测较稳定，变异系数为0.25；其他公式预测平均值在1.11～1.40，变异系数在0.25～0.35。

从图2可知：王建超公式和Rombach公式预测结果拟合直线的相关系数分别为0.91和0.917，拟合结果最好；袁爱民公式和AASHTO公式拟合的相关系数为0.855和0.868，相对而言拟合差于其他公式。

4.2 键齿胶接缝剪切破坏分析

针对键齿胶接缝的受力性能，国内外学者进行了大量的键齿胶接缝试件的直接剪切试验。键齿胶接缝的直剪破坏一般具有以下特征：与干接缝不同的是，胶接缝试件发生直剪破坏时，几乎是多个键齿同时剪断，破坏面几乎贯穿整个接触面，因此可以理解为整个剪切面的破坏；胶接缝的剪切破坏主要发生于胶层附近的混凝土，即胶层与混凝土的接合面为受力薄弱点。

典型的荷载-竖向相对滑移曲线和键齿接缝破坏模式见图3，加载过程为：荷载-位移在加载初期基本呈线性关系，随后裂缝开展导致试件刚度略微下降，曲线斜率也随着斜裂缝的发展开始明显下降，最后键齿混凝土压碎，达到试件的极限承载力。胶接缝的破坏面并不明显，但混凝土内部微小裂缝充分开展，基本贯通整个剪切面，胶层的作用使键齿裂缝的发展和破坏发生间隔时间很短。

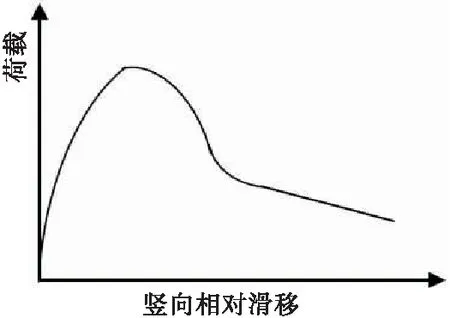
(a) 荷载-滑移曲线

4.3 计算模型

已有一些的胶接缝承载力计算公式表示形式说明：绝大部分的计算公式将承载力表示为与整个接缝总面积Aj成正比，无法明确键齿部分和竖直剪切面的贡献，缺乏明确的物理含义，而且忽略了键齿个数的影响，因此有必要提出更为合理的表示形式。本节根据接缝的受力特征和上述承载力计算公式的形式，将胶接缝直剪承载力模型可表示如下：

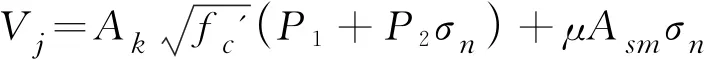
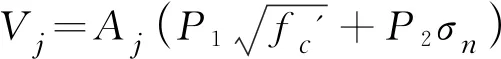
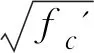
基于上述计算模型和已收集的试验数据，通过数学拟合可以得到不同模型的参数值，各模型参数分别列于表3，同时试验值与各个模型预测值的比值与变异系数也列于表3。4种计算模型的预测值与试验结果的关系见图4。

(a) 模型一

表3 计算模型对比Table 3 Comparisonofcalculatedmodes模型P1P2μ平均值标准差变异系数模型一1.178 30.273 91.41.000.230.23模型二1.189 31.739 91.41.000.230.23模型三0.731 70.250 2—1.000.250.25模型四0.747 61.615 4—1.000.250.25Bakhoum0.6471.36—0.930.250.27卢文良0.551.4—1.270.320.25袁爱民0.561.2—1.260.320.25

由表3可知：对比模型一和模型二，模型一的参数P1较为接近，而参数P2较模型二小，说明模型二较模型一更大程度考虑了侧向应力的抗剪贡献，模型三和模型四也有类似的差异。模型一、二较模型三、四的预测变异系数更小，说明了这种公式形式比目前应用较多的公式形式更好，可以更好地反应键齿的作用，同时明确了各部分的抗剪贡献。Bakhoum公式、卢文良和袁爱民公式与模型四具有相同的结构形式，仅参数取值有一定差异。

对比已有规范公式或其他学者给出的计算公式，本文基于大量试验数据所提出的4种计算模型可以更为准确地预测键齿胶接缝的抗剪承载力。

4.4 接缝抗剪强度影响因素分析

显然，当混凝土梁设置接缝时，其抗剪承载力会小于整体浇筑截面的抗剪承载力，因此有必要量化键齿胶接缝相对于整体浇筑截面的抗剪折减系数，从而进一步指导节段预制拼装桥梁的接缝设计。对于整体浇筑截面而言，其直剪承载力计算公式如下[7]：

(10)

式中：参数意义同上。

a.侧向应力的影响。

随着接缝形式(这里指键齿面积Ak与接缝面积Aj的比值)和侧向应力σn的变化，这里以Ak与Aj的比值为0.3为例，给出本文所提出的4种计算模型的接缝抗剪承载力与整体浇筑截面抗剪承载力的比值变化，如图5所示。

图5 不同应力状态下各模型抗剪承载力比值

由图5可知：4种计算模型对于接缝抗剪承载力的预测具有一定差异，模型四相对而言计算的直剪承载力较大；当侧向应力超过10 MPa后，接缝的抗剪承载力趋于稳定，因此设计时应合理选择接缝所承受的侧向应力，从而最大程度减少接缝的抗剪折减系数。

b.接缝形式的影响。

以模型一为例，这里给出不同的接缝形式(Ak与Aj的比值为0.2～0.5)，在不同侧向应力下接缝抗剪承载力与整体浇筑截面抗剪承载力的比值变化，如图6所示。

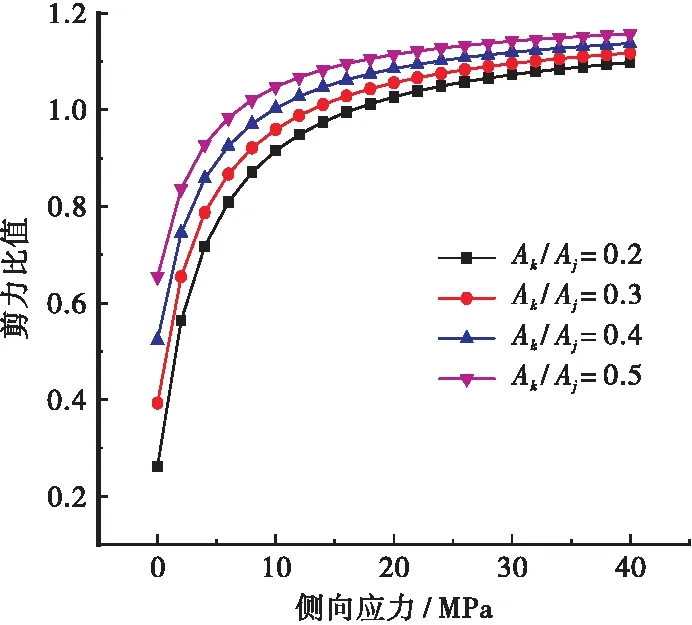
图6 不同接缝形式抗剪承载力比值

由图6可知：随着键齿与接缝面积比值的增大，相应的抗剪承载力与整体浇筑截面的抗剪承载力之比也越来越大；设计时在满足相应要求的前提下应尽量增加键齿的面积以提高接缝的抗剪承载力。

c.混凝土强度的影响。

以模型一为例，这里给出不同强度的混凝土接缝在不同侧向应力下接缝抗剪承载力与整体浇筑截面抗剪承载力的比值变化，如图7所示。

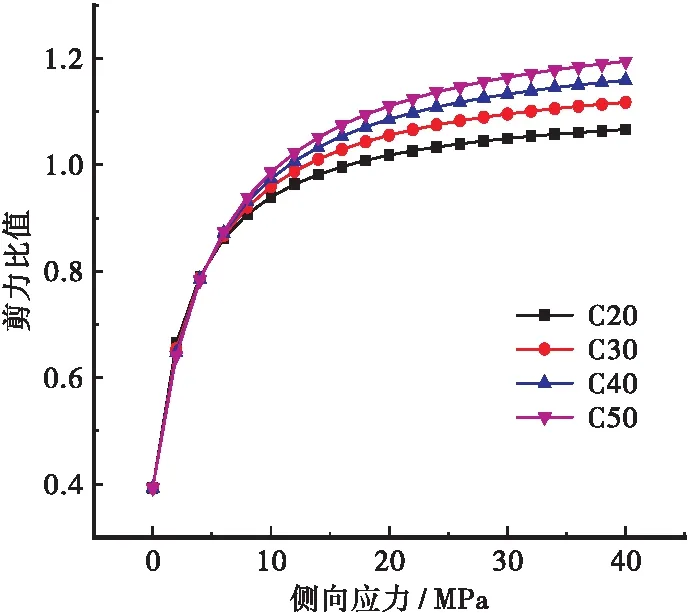
图7 不同混凝土强度抗剪承载力比值

由图7可以看出：当侧向应力较小时，接缝相对整体浇筑截面的抗剪影响程度基本相同；随着侧向应力的增大，混凝土强度越高，接缝对直剪承载力的削弱越小。

5 结论

本文将节段预制拼装桥梁的键齿胶接缝作为研究对象，收集了国内外共53组试验数据与试验参数，对已有键齿胶接缝的抗剪承载力计算公式的适用性和准确性进行了评价和分析。根据已有研究理论和试验数据总结提出了4种抗剪承载力计算模型，并拟合得到相应的计算公式。得到主要结论如下：

a.本文评价的公式中，除Bakhoum公式的预测结果偏不安全外，试验结果与其余公式的预测值的比值都大于1，可以保证计算结果的安全性，但是Bakhoum公式预测结果平均值最接近1，准确性最高。

b.本文评价的公式中，Rombach、卢文良和袁爱民提出的公式预测最为稳定，变异系数为0.25；其他公式预测平均值在1.11～1.40，变异系数在0.25～0.35。

c.本文提出的4种计算模型反映了已有计算公式的基本模型，模型四与已有公式之间仅有参数取值差异。本文提出公式可以准确预测键齿胶接缝的直剪承载力，试验数据与4个公式预测的比值均为1，模型一、二的变异系数为0.23，模型三、四的变异系数为0.25。

d.侧向应力、接缝形式和混凝土强度是影响键齿接缝抗剪的主要因素，设计时建议在合理范围内选用较大的侧向应力和混凝土强度，同时尽量增大键齿面积。