圆砾地层中深基坑双排桩支护结构受力变形计算分析
欧孝夺,白 露,江 杰,罗方正
(1. 广西大学 土木建筑工程学院,广西 南宁 530004;2. 工程防灾与结构安全教育部重点实验室,广西 南宁 530004;3. 广西金属尾矿安全防控工程技术研究中心,广西 南宁 530004;4. 中国建筑第八工程局有限公司,广西 南宁 530028)
0 引言
我国华南、西南等地区广泛分布有上覆于泥岩的一套河流相冲积地层——圆砾地层,其粒径大,强度高,有强透水性,埋深一般为8~15 m。近年来,城市地下工程建设不断发展,大量圆砾层地区深基坑工程也随之涌现。然而城市建设对基坑变形控制有着严格要求,大量的工程事故与经验教训表明,基坑支护选择要坚持安全、合理、经济的基本原则。双排桩支护是由前、后排桩与连系梁组成的悬臂式超静定空间门架结构,它能有效地限制侧向变形,不需要内支撑,受力均匀且发挥了整体空间效应作用;以其变形小、施工方便、建设速度快等优点获得了工程设计人员的青睐,在深基坑工程中广泛应用。但目前在圆砾地层中应用双排桩支护较少,其有关机理和计算模型仍有待研究[1-2]。
目前对双排桩的理论计算已有大量研究,主要可分为基于经典土压力的计算模型、基于Winkler弹性地基梁的计算模型和基于土拱理论的计算模型。张弘[3]等提出了修正系数法,基于经典土压力理论,对前、后桩的桩间土压力采用经验系数的方法分配,桩后土压力使用朗肯土压力与经验折减进行计算;何颐华[4]等提出体积比例系数法,按双排桩桩间滑动土体与桩后土体体积比例关系来确定桩体所受的土压力;熊巨华[5]等提出等效刚度法,把前后排桩和桩间加固土体刚度进行等效叠加;经典土压力模型计算简单,但没有考虑桩土相互作用,与实际工程存在一定偏差。刘钊[6]等提出Winkler弹性地基梁计算模型,将双排桩假定为竖向放置的弹性地基梁,桩体所受水平荷载采用土弹簧进行模拟,该法考虑了桩土相互作用,但计算较为复杂,不适用侧向变形较大的支护结构;郑刚[7]等基于Winkler弹性地基梁,把土压力作用与约束都用弹簧来模拟,利用杆系有限元法计算其变形和内力;季伟[8]等在总结前人的基础上,改进了一种传统的剪切滑移面,采用体积比例系数法分配桩间土对前、后排桩的土压力;张玲[2]等充分考虑桩桩相互作用,把桩间与前排桩前土压力全部看做弹性地基梁建立微分方程进行求解,得出相关结论。戴智敏[9]等基于土拱理论于桩间土对前、后排桩的作用进行研究,采用一个假定的滑裂面将坑外被支挡土体划分为两部分,在假定的滑裂面以上土体采用土拱理论分析,以下部分采用土抗力法分析。该法虽然考虑了桩土的相互影响与空间效应,但对于土拱效应而引起的桩侧土压力与实际仍有一定误差。
由于圆砾地层中土黏聚力为零,随着基坑开挖颗粒松动较大,而以上学者对双排桩的研究未能充分考虑随着基坑开挖桩体发生变形时土压力的作用形式变化,不适用于的圆砾地层深基坑双排桩的分析与计算。为能够更合理体现出原砾地层中深基坑双排桩的受力变形情况,根据一类适用于圆砾地层开挖破坏滑移面,将匡飞[10]等提出能量法计算桩间土压力,以及黄忠铭[11]等提出用弹性附加应力对后排桩底土压力计算模型进行结合,对规程中双排桩桩间和桩侧土压力作用进行改进,应用Winkler假定计算模型对圆砾地层中深基坑双排桩支护结构内力与其变形展开研究。
1 计算模型
1.1 现行规程中的计算模型
《建筑基坑支护技术规程》JGJ120-2012[12](本文简称规程)双排桩计算模型如图1所示。
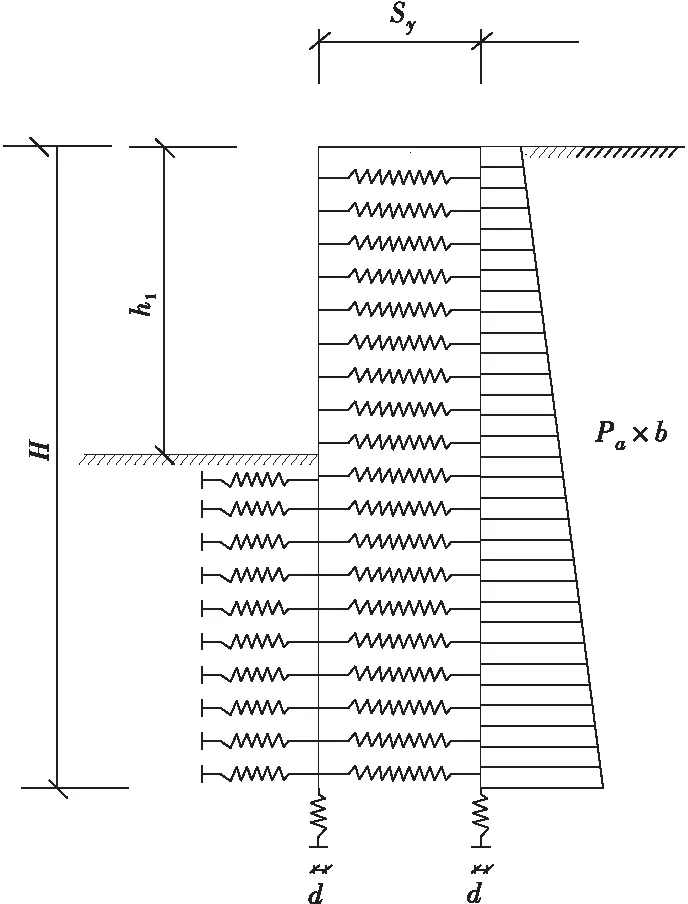
图1 规程中双排桩的计算模型
规程中桩前土体对前排桩采用弹簧来模拟土抗力,其所受土体作用反力强度ps为:
ps=ksν+ps 0
(1)
式中:ν为前排桩土反力计算点的土体水平压缩位移值,m;ks为土体水平反力系数,kN/m3;ps 0为初始土反力强度,kPa,可按朗肯被动土压力计算,其中:
(2)
ks=m(z-h1)
(3)
式中:z为土体深度;h1为基坑开挖深度;γ、c分别为土的重度、黏聚力;Kp为被动土压力系数,Kp=tan2(45°+φ/2),其中φ为土体摩擦角;m为土的水平反力系数的比例系数,可按当地的规范取值,当没有试验和经验取值时,按下式进行计算:
(4)
式中:νb为支护结构在坑底的水平位移量,mm,若底部水平位移不大于10 mm,可按νb=10 mm取值。图1中pa为朗肯主动土压力,Sy为双排桩排距,d为桩径,b为双排桩计算宽度,可按规程[12]进行相应取值。
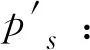
(5)
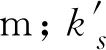
可以看出,规程计算模型存在以下不足[11,13]:
a.规程计算模型认为桩间土对前、后排桩作用力相等,采取朗肯土压力计算。而当双排桩发生水平变形时,桩间土对前排桩作用为主动土压力形式,对后排桩作用为被动土压力形式且作用极小,可见这二者并不相等,与实际情况较为不符。
b.规程中桩间土水平刚度系数采取桩间土压缩模量与其宽度的比值,为一常量;而随着基坑开挖桩间土水平刚度系数与土层深度、土层性质等是有关的。
c.规程中桩后土压力计算模型容易发生后排桩踢脚的现象,不适用于深基坑或支护结构嵌固深度较深的情况。
1.2 计算模型的改进
a.圆砾地层破坏滑移面。
基坑开挖后,对于嵌固深度较大的支护结构,嵌固部分侧移较小,而开挖面以上的变形相对较大。因此假想存在一剪切滑移面,在滑移面以上桩体主要抵抗土的滑动作用;滑移面以下桩体主要承受桩周土的挤压作用,采用弹性土抗力法来求解。由于圆砾土层粒径大,黏聚力为零,当桩体变形后,圆砾间有较强粒间锁固效应,因地层松动而形成的松动区比黏性土和砂土更为显著。根据吕玺琳[14]等对饱和圆砾地层盾构隧道开挖面稳定性进行物理模型试验,通过研究饱和圆砾地层开挖支护压力变化与地层变形过程,得出采用宽楔形体模型预测圆砾地层开挖形成的滑移区更为合理。本文认为圆砾地层中开挖面破坏模式为楔体加筒仓结构,倾角约为45°+φ/2。
b.桩间土压力计算。
计算模型如图2所示,基坑开挖深度为h1,前、后排桩嵌固深度h2,双排桩间距为s,θ为滑裂面与水平的夹角,可知θ=45°+φ/2。由于存在滑裂面的影响,当双排桩桩间土体处于塑性流动或剪切滑动状态时,假定滑裂土体ABFD在滑裂面上应变的速率为v,其矢量与滑裂面BD成φ角。前排桩对滑裂面土体的反力PC与前排桩的法线成η角[10]。
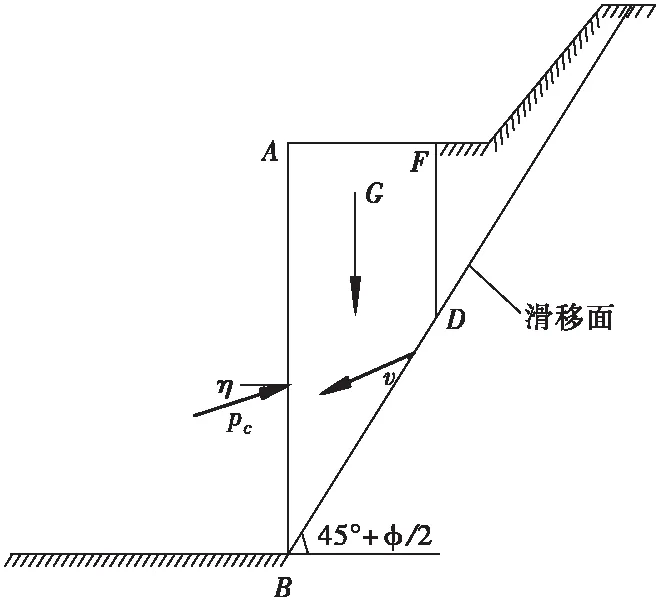
图2 桩间土压力计算模型
滑裂面以上桩间土体ABDF的自重G为:
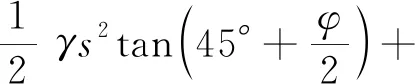
(6)
自重力G所做的功为:
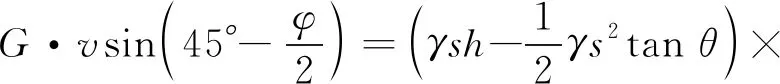
(7)
外力Pc在水平方向所做的功为:
(8)
外力Pc在竖直方向所做的功为:
(9)
故外力所做的功为以上3个部分之和,即:
(10)
在滑裂面BF任一点处消耗的能量(内功)为:
(11)
根据外力所做的功与内部消耗的能量相等的原理,即W=M,消去v可得:
(12)
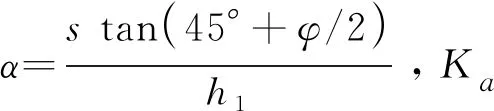
(13)
若不考虑土体表面荷载,假定桩间土压力强度按线性分布,则任意深度处前排桩所受的主动土压力强度大小为:
(14)
c.桩后土压力计算。
当基坑尚未开挖时,双排桩在静止土压力作用下处于平衡状态。随着基坑逐步开挖,双排桩受到卸荷而引起的附加应力作用。由于在深基坑中,双排桩嵌固深度较大,在滑移面以下,土体侧向水平变形较小,近似受静止土压力作用,若按照规程计算土压力,后排桩容易产生踢脚现象。根据地基附加应力的原理,桩端底部受到土压力作用沿滑移面以下深度减小至q/2,其中q为开挖深度位置土压力中的竖向应力[12]。
这种土压力作用模式计算方法是根据弹性地基附加应力确定的,基坑开挖实际上是地基荷载释放的过程,可根据两阶段法看做开挖面以上基坑外侧荷载对坑底产生附加应力,应用弹性力学中半无限体在边界上均布荷载作用对基坑底部的应力求解。半无限体在边界上受法向均布力为微小段集中荷载在0到+∞的积分,即:
(15)
积分后得:
(16)
当y=0时,由式(16)可得σy=-q/2,即认为地基水平方向附加应力大小均为q/2。
后排桩土压力计算模型如图3所示:
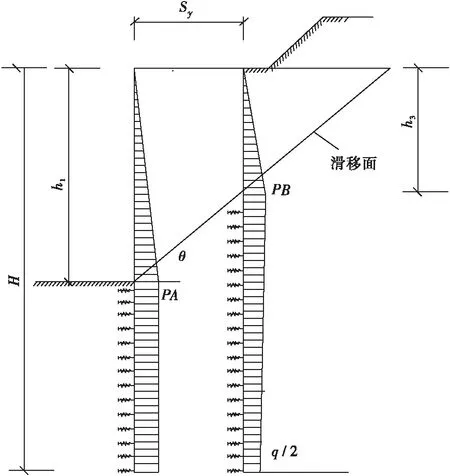
图3 本文计算模型
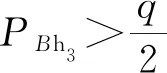
(17)
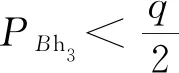
(18)
式中:q为开挖深度位置土压力中的竖向应力,q=γh3+q0,其中,γ计算点以上土体的重度当量值,q0为地面超载。
2 微分方程的建立与求解
2.1 微分方程的建立
a.前排桩挠曲变形微分方程。
滑移面以上:
(19)
滑移面以下:
(20)
b.后排桩挠曲变形方程。
滑移面以上:
(21)
滑移面以下:
(22)
2.2 微分方程的求解
2.2.1滑移面以上微分方程求解
假设前排桩桩顶的水平位移、转角、弯矩、剪力y0、φ0、M0、Q0,对式(19)和式(21)进行积分求解,可得:
a.前排桩滑移面以上挠曲变形方程。
(23)
则转角、弯矩、剪力分别为:
φ=y′,M=EIy″,Q=EIy‴
(24)
b.后排桩滑移面以上挠曲变形方程。
对于排距较小且连系梁刚度较大的双排桩结构,可假设连系梁为刚体,因此根据前、后排桩协调关系,可得后排桩桩顶处水平位移、转角、剪力、弯矩分别为y0、φ0、-M0、-Q0,可得:
(25)
2.2.2滑移面以下微分方程求解
对滑移面以下式(20)和式(22)求解时利用幂级数计算方法来求解,假设曲线方程为:
y=a0+a1x+a2x2+a3x3+…+anxn=
(26)
那么:
将式(26)代入式(20)可得:
(27)
根据式(27)可确定所有系数之间的关系,即用a0,a1,a2,a3之间的关系来表示a4,a5,a6…an,式(26)为:
y=a0f0(z)+a1f1(z)+a2f2(z)+a3f3(z)
(28)
由式(23)、式(24)可求得前排桩在滑移面处(z=h1)的位移、转角、弯矩、剪力分别为yh1、φh2、Mh1、Qh1,可得滑移面以下曲线变形方程:
(29)
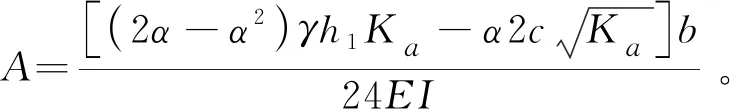
(30)
引入:
[r(k-2)-n]…{r[k-(k-1)]-n}
(31)
式中:n=0,1,2,3…;r=5,10,15,20…(r>n)。
由式(24)、式(25)可求得后排桩在滑移面处(z=h3)的位移、转角、弯矩、剪力分别yh3、φh3、Mh3、Qh3,即可得滑移面以下曲线变形方程:
(32)
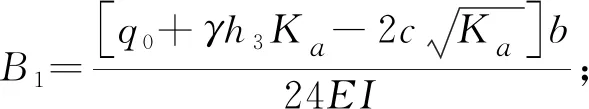
(33)
根据式(24)求得前、后排桩滑移面以下的转角、弯矩和剪力方程。
2.3 引入边界条件
目前对于桩底的约束条件考虑有铰接约束、竖向约束和自由端,当嵌固深度较深时,桩体底部所受土压力较小,假定受到铰接约束作用,即弯矩和位移为零0。
a.由于前排桩桩底位移为零:
y12(z=H)=0
(34)
即:
y12(z=H)=yh1f0(z)+φh1f1(z)+
(35)
b.由于前排桩桩底弯矩为零:
(36)
即:
(37)
c.由于后排桩桩底位移为零:
y22(z=H)=0
(38)
即:
y22(z=H)=yh3f0(z)+φh3f1(z)+
B2f5(z)=0
(39)
d.由于后排桩桩底弯矩为零:
(40)
即:
(41)
e.由于前后排桩在滑裂面处位移y,转角φ,弯矩M,剪力Q具有连续性,即在滑裂面处位移、转角、弯矩、剪力应是相等的。
由式(35)、 式(37)、 式(39)、 式(41)联合解方程组可以求得桩顶水平位移、转角、弯矩和剪力y0、φ0、M0、Q0的值,将其代入式(23)、 式(25)、 式(29)、 式(32)、 式(28),可得前、后排桩水平位移和弯矩关于深度的曲线方程,再代入z值可得双排桩沿深度各点处的内力和变形。
3 工程实例验证
3.1 工程概况
南宁市轨道交通4号线那洪立交站位于南宁市那洪大道与壮锦大道交叉路口。选取其中一个剖面3-3进行计算,采用φ800@1 200双排桩+止水帷幕+坑内疏干井的支护形式。基坑开挖深度14.05 m,围护桩桩顶位置设置有1∶1放坡段,坡高2.8 m,坡脚距围护桩顶设置1.3 m宽平台。围护桩采用抗渗等级为P8的水下C35混凝土、连系梁厚度为450 mm,连系梁和冠梁均采用C35混凝土。基坑范围内无重要管线,该基坑围合区部分如图4所示。
图4 围合区部分基坑平面图
基坑开挖过程中在冠梁顶端布设监测点,对基坑相应位置处进行水平位移监测和沉降观测,针对双排桩沿围合区共布置有11个监测测点,每个测点的监测内容包括:桩顶沉降、桩体弯矩、前排桩体水平位移、地下水位和地表沉降的监测。
工程地质勘察对各土层特征与工程性质指标如表1所示。该剖面地层圆砾填土层厚为2 m,含黏性圆砾层厚为7.6 m。圆砾土层的主要特征为密实度高,骨架构成主要为中粗砂颗粒;承载力较高,施工特性介于砂土和岩石之间;具有强透水性,粒径变化较大,一般5~40 mm,地层较多空隙,渗透系数较大。双排桩支护剖面如图5所示。
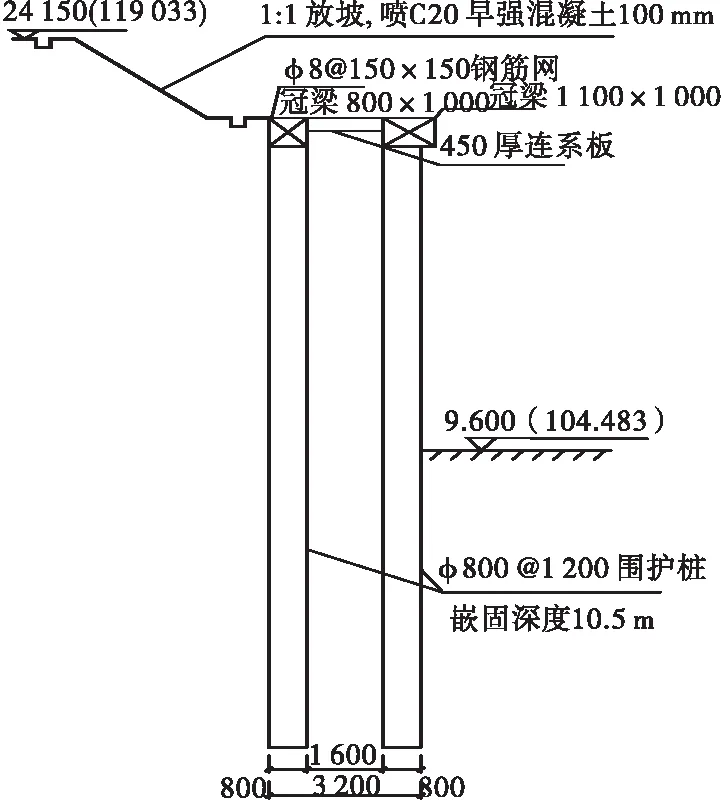
图5 双排桩支护结构剖面图
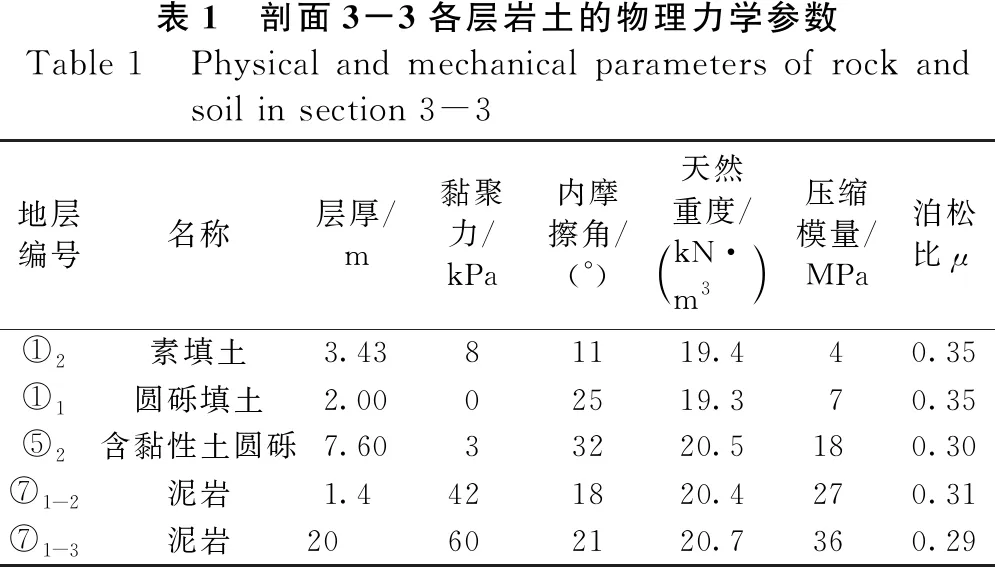
表1 剖面3-3各层岩土的物理力学参数Table 1 Physical and mechanical parameters of rock and soil in section 3-3地层编号名称层厚/m黏聚力/kPa内摩擦角/(°)天然重度/kN·m3 压缩模量/MPa泊松比μ①2素填土3.4381119.440.35①1圆砾填土2.0002519.370.35⑤2含黏性土圆砾7.6033220.5180.30⑦1-2泥岩1.4421820.4270.31⑦1-3泥岩20602120.7360.29
3.2 计算结果分析
3.2.1内力计算对比分析
本文改进模型双排桩弯矩对比图如图6所示,可以看出对于前排桩弯矩最大值,本文改进模型计算为1 668 kN·m,监测结果为1 483 kN·m,规程计算为2 634 kN·m;对于后排桩弯矩最大值,本文改进模型计算为1 648 kN·m,监测结果为1 530 kN·m,规程计算为1 016 kN·m。与规程计算结果相比,本文改进模型计算结果与监测数据更为接近,其弯矩变化规律、反弯点与其数值大小跟监测数据更加吻合,可见本文改进模型相比规程算法其准确性有很大的提高。
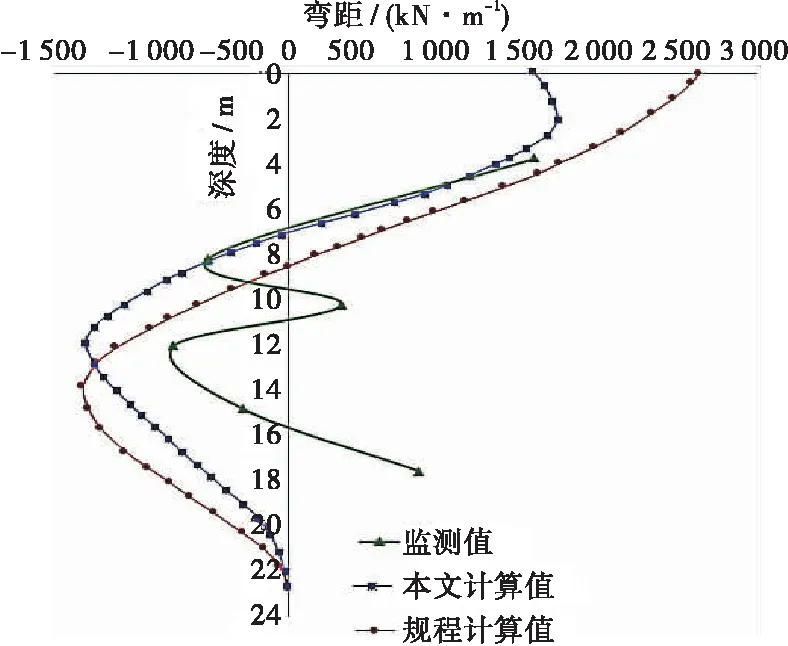
(a) 前排桩弯距图
3.2.2水平位移计算对比分析
本文改进模型水平位移计算结果同规程算法和监测数据如图7所示,本文计算时双排桩结构类似于悬臂梁,因此前、后排桩最大位移均发生在桩顶,大小为42.29 mm,规程计算桩顶位移为59.23 mm,而实际监测桩身最大位移发生在桩深5.5 m处,为21.32 mm,桩顶位移为17.91 mm。由于本文忽略连系梁的作用,在桩顶部位计算结果偏于保守,但在6 m以下桩体变形大小与监测数据基本吻合,而规程计算位移值偏大。因此本文改进模型计算的侧移大小与变化规律比规程算法对于基坑变形控制更具有借鉴性。
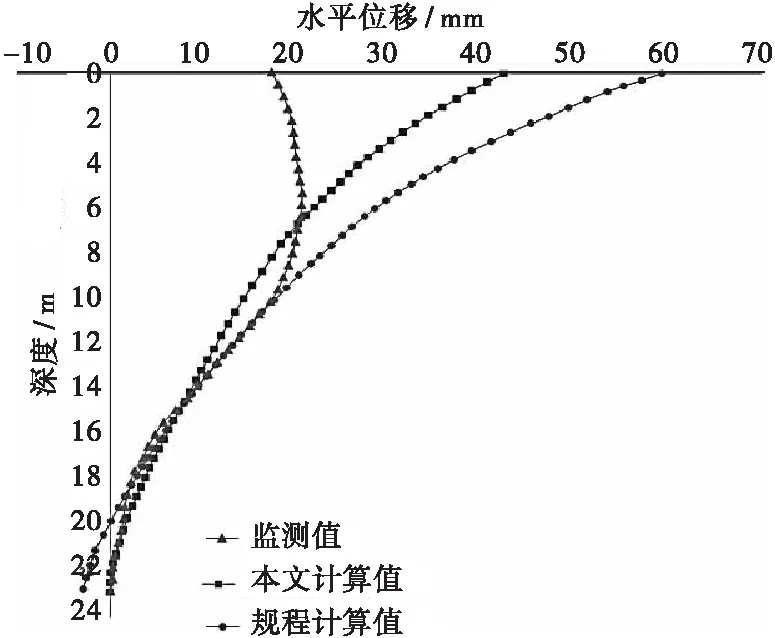
(a) 前排桩位移图
4 结论
本文对一种富水圆砾地层中深基坑双排桩支护结构内力和变形进行理论研究。结合南宁市轨道交通4号线那洪立交站附属围合区深基坑双排桩支护工程实例验证改进模型的合理性,得出以下结论:
a.本文充分考虑了基坑变形后的桩土相互作用,应用能量法原理计算桩间土体对前排桩的土压力作用,同时考虑了对于嵌固深度较大的双排桩支护,使用弹性地基附加应力对规程中后排桩滑移面以下土压力进行改进,避免了后排桩出现踢脚的现象,可见该法更符合实际受力情况,在针对圆砾地层深基坑双排桩支护结构计算与变形控制方面具有一定的参考价值。
b.相对于规程算法,本文模型计算的桩体内力和变形在数值与变化规律方面更接近监测数据,因此本文改进计算模型准确性有很大的提高,能有效的改善规程中存在的问题。
c.实际工程中土层分布较为复杂,而在计算时,土体水平抗力系数k和土体相关力学参数取值相对简单,使得部分桩体计算的弯矩和侧移变化规律与监测数据存在一定误差;此外,对于超大基坑存在尺寸效应、土体开挖分段施工对土压力造成的影响等问题还需今后进一步深入研究。

