多部件非均匀锈蚀对钢混组合梁承载力退化的影响研究

陈 冠

(湖南路桥建设集团有限责任公司，湖南 长沙 410018)

0 引言

钢混组合梁桥由于其充分发挥了钢材、混凝土的材料特性，具有良好的力学性能，可以采用工厂化预制生产等特点，近年来广泛应用于大中小桥梁的建设。而钢材与混凝土材料的良好黏结，是保证二者协同工作的前提，当钢混组合结构中栓钉、钢筋等材料由于环境因素发生锈蚀时，会显著降低结构承载力，降低其耐久性和安全性[1-3]。

针对构件锈蚀问题，国内外学者进行了大量研究工作：LI[4]通过对混凝土构件预留孔洞并加压的方式模拟了钢筋均匀锈蚀产生的锈胀力，并对锈胀力与混凝土开裂的关系进行了分析；张猛[5]等采用有限元法(FEM)建立了未锈蚀钢筋混凝土简支梁静力计算模型，分析了钢筋不同锈蚀率与简支梁的承载力退化的关系；ALONSO[6]等利用电化学加速的方式实现了钢筋加速锈蚀，定量分析了保护层开裂与钢筋锈蚀率之间的关系；徐亦冬[7]等通过蒙特卡洛方法建立了随机骨料模型，实现了钢筋锈胀细观FEM模拟，分析了锈蚀层厚度与裂缝分布的关系；MARK[8]等根据理论计算，提出了栓钉锈蚀后的钢混组合梁抗弯承载力简化计算方法，并利用相关文献试验结果，验证了该简化算法的正确性；LIU[9]等通过试验，对栓钉锈蚀类型进行了归纳，并对栓钉锈蚀后组合梁力学性能进行了分析。上述试验中，部分学者采用电化学加速试验的方式实现钢筋的快速锈蚀，但此方法与实际结构中钢筋的锈蚀层分布存在差异，且难以对锈蚀后的结构进行参数测量；而采用有限元法模拟钢筋锈蚀则往往以均匀锈蚀进行简化，而实际结构中锈蚀往往是非均匀的，二者在锈胀力上存在显著差异。对钢混组合梁栓钉的锈蚀研究目前也存在着上述问题，且对于实际结构，如若其普通钢筋存在锈蚀，则往往栓钉也会发生锈蚀，而目前尚未见到考虑2种部件锈蚀对结构性能耦合影响的研究。

为了明确钢混组合梁桥栓钉、钢筋等部件非均匀锈蚀产生的锈胀力对结构性能的影响，并考虑2种部件发生锈蚀下的效应耦合，本文通过理论推导，对FEM法计算均匀、非均匀锈蚀构件模型的正确性进行了验证，并利用通过验证的模型分析了单部件、多部件非均匀锈蚀耦合和不同锈蚀率对结构承载力的影响，为计算锈蚀后钢混组合梁承载力提供参考，为定量评估锈蚀后钢混组合梁安全和耐久性提供依据。

1 锈胀应力场理论分析

当栓钉、钢筋发生锈蚀后，其锈蚀产物相较于自身未锈蚀体积发生膨胀，从而产生结构细部锈胀力[10]，而目前对于锈胀力的计算大致包括试验、理论计算、FEM模拟3种方式，而采用试验的方式最终需落脚于相关理论的提出，同时锈胀力计算理论也是指导FEM模拟的关键。为此，现对均匀锈蚀与非均匀锈蚀下混凝土锈胀应力场进行分析，并结合理论建立FEM模型，为下文定量分析奠定基础。

1.1 均匀锈蚀

如图1、图2所示参考系建立平面内钢筋/栓钉与混凝土结构力学模型，将混凝土视为均匀无限大板，当距离钢筋/栓钉周围存在保护层时，通过该保护层将板切割为2个轴对称半无限大板，此时保护层存在面力q，通过反向叠加-q即可消除面力q对锈胀应力场的影响(图1中，Δ表示锈胀位移，R为钢筋/栓钉半径，c为保护层厚度，d为钢筋中心距保护层的距离)。

图1 钢筋/栓钉与混凝土均匀锈蚀平面力学模型

图2 钢筋/栓钉与混凝土非均匀锈蚀平面力学模型

由弹性力学，轴对称问题在极坐标系下的应力解与位移解为：

(1)

式中:σr为径向应力；σθ为环向应力；τrθ为剪应力；ur为径向位移；uθ为环向位移；A、B为待求常数；E为弹性模量；v为泊松比。

考虑到图1中无限远处径向应力为0，且在r=R处位移为Δ，则有：

(2)

将式(2)代入式(1)并转化为直角坐标系，有：

(3)

当x=-d时，参考文献[11]给出了考虑保护层边界处面力q的混凝土保护层表面应力分量表达式：

(4)

1.2 非均匀锈蚀

根据文献[11]对自然条件锈蚀钢筋锈蚀层厚度的电镜观测结果，椭圆曲线能较好地拟合锈蚀层厚度分布情况，对极坐标系下椭圆曲线公式a2ρ2sin2θ+b2ρ2cos2θ=a2b2(a为长半轴长，b为短半轴长)，其上半圆径向位移为：

(5)

式中:e为椭圆离心率。

根据文献[12]，弹性力学平面问题位移型解答为：

(6)

其相容方程为：

(7)

参考文献[13]给出的位移函数形式φ=f(t)(θ+sin 2θ)，将其代入相容方程，并考虑位移函数的有界性，则有：

φ=(A+Bt)e-tθ+(Ce-t+De-3t)sin 2θ

(8)

式中:A、B、C、D为待定系数。

(9)

1.3 解析解与FEM结果验证

现根据1.1节和1.2节推导应力分量表达式，采用FEM方法进行验证。分别建立考虑均匀锈胀力的平面应变模型(Model-1)和考虑非均匀锈胀力的平面应变模型(Model-2)， 主要几何参数见图3(a)，其中混凝土强度等级为C25，弹性模量取28 000 MPa，泊松比为0.2，钢筋/栓钉直径为16 mm，弹性模量取200 GPa，泊松比为0.3，锈蚀层厚度Δ=0.001 mm，采用二阶八节点四边形平面应变单元CPE8划分网格，全局种子尺寸为2 mm，局部种子尺寸为0.25 mm，并对钢筋/栓钉和靠近该处的混凝土网格进行加密，以使计算结果更为精确，网格划分见图3(b)。

通过定义以钢筋/栓钉中心为原点的局部极坐标系，在Model-1钢筋/栓钉与混凝土的环向接触面施加相同均匀径向位移以模拟均匀锈胀力[如图3(c)所示]， 在Model-2中按式(5)建立以局部坐标系为变量的解析表达式场，并对钢筋/栓钉与混凝土的环向接触面施加以该解析场为分布的径向位移以模拟非均匀锈胀力[如图3(d)所示]。此外，对两种模型远离钢筋/栓钉的左侧约束所有自由度。

(a)几何尺寸

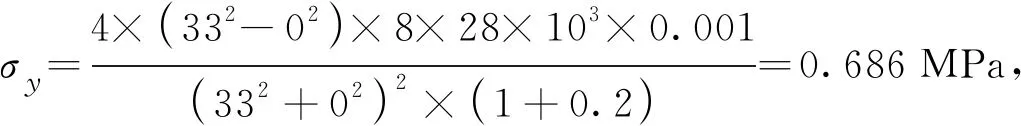
由图4可知，均匀锈胀力与非均匀锈胀力作用下剪应力分量τrθ=0，但环向、径向应力分量随角度的分布存在一定差异，均匀锈胀力作用下环向、径向应力分量绝对值基本保持不变，且互为相反数，而非均匀锈胀力作用下环向、径向应力分量分布形式相同，二者相差约为一常数，且应力分量绝对最大值相等。对比均匀锈胀力与非均匀锈胀力，可以发现非均匀锈胀力作用应力分量显著大于均匀锈胀力作用，对于本例，非均匀锈胀力下环向、径向应力峰值约为均匀锈胀力下的1.75倍，因此，对于钢混组合梁钢材锈蚀的考虑，采用均匀锈蚀的形式则计算结果偏不保守，采用非均匀锈蚀的形式更为贴合实际，且计算结果更能反映锈胀力对结构性能退化的影响。

(a) Model-1环向应力σθ云图

2 锈蚀深度与有效截面的归一化表达

第1节中以锈蚀层厚度(Δ)体现了钢筋/栓钉锈蚀程度，并对指定锈蚀层厚度的混凝土保护层锈胀应力场进行了理论分析与FEM验证。但在目前相关研究中，多以钢材部件锈蚀率对部件的锈蚀程度进行描述[14]，因此，需对锈蚀层厚度与锈蚀率建立数学关系，以更为直观地表达钢筋/栓钉的锈蚀程度对结构承载力的退化影响；此外，当钢筋/栓钉发生锈蚀后，其有效截面受到削弱，可对锈蚀后的有效截面与锈蚀率建立数学关系，以更为准确考虑钢筋/栓钉的锈蚀程度对结构承载力退化影响。现分别建立锈蚀率与锈蚀深度、有效截面的关系。

对于非均匀锈蚀，其钢筋/栓钉的锈蚀深度δ与锈蚀层厚度Δ的关系[15]为：

(10)

式中:n为钢筋/栓钉的锈蚀产物膨胀系数，取2～4。 而钢筋/栓钉的锈蚀率λ可写为锈蚀产物的质量m′与其初始质量m之比：

(11)

且对于等截面钢筋/栓钉，可将质量转化为面积的关系，锈蚀后钢筋/栓钉截面被削弱，对于全圆周发生不均匀锈蚀的情况，其轮廓线由圆曲线变位长半轴为b，短半轴为b-δ的椭圆曲线[图5(a)]，对于半圆周发生不均匀锈蚀的情况，其上半部分轮廓线由半圆曲线变位长半轴为b，短半轴为b-δ的半椭圆曲线[图5(b)]，对于其他更为复杂的不均匀锈蚀，也可按类似方法，利用面积比例关系建立锈蚀层厚度与锈蚀率的关系。全圆周、半圆周发生不均匀锈蚀的情况，锈蚀产物的截面积为初始面积与锈蚀后有效面积之差，则锈蚀率以面积之比可分别表示为：

(a) 全圆周不均匀锈蚀

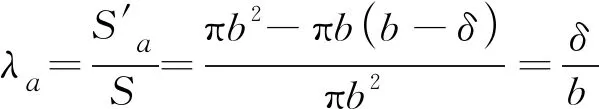
(12)

(半圆周)

(13)

因此，通过式(10)、 式(12)、 式(13)即可建立锈蚀率与锈蚀层厚度之间的关系，且式(12)同时给出了锈蚀率与锈蚀削弱后钢筋/栓钉有效截面的关系，可在后续计算中直观地体现部件锈蚀率对结构承载能力的影响。

3 部件锈蚀对结构承载力退化的影响

当结构中钢筋/栓钉发生锈蚀后，一方面其锈胀力增大了混凝土保护层界面的应力，可能引发结构开裂等病害；另一方面削弱了钢筋、栓钉的有效截面，降低了结构自身的抗力。对此，现以某高架桥为工程背景，分析部件锈蚀对结构承载力退化的影响。

3.1 工程概况

某高架桥第二联采用3×29.6 m钢混组合梁，梁体以路线中心为轴，双向1.5%横坡。主梁采用“工字型钢主梁+预制混凝土桥面板+现浇桥面板”组合结构。桥面板上未设置桥面现浇层，采用9 cm沥青混凝土铺装。桥梁的双向横坡为1.5%。钢梁下翼缘按横向按平坡布置。桥梁全宽24 m，横向布置8片工字钢主梁，工字钢主梁间距3 m，外侧桥面板挑臂1.5 m。钢板组合梁全高150 cm，高跨比为1/19.7，主要几何参数见图6。

图6 钢混组合梁标准截面几何参数(单位：mm)

3.2 FEM模型

以上述工程背景，基于第1节理论验证的FEM建模方法建立仿真模型，考虑到结构尺度较大，且多部件锈蚀发生区域为工字钢梁顶部混凝土板，为简化计算提高效率，对相关尺寸进行简化，取单片工字钢梁与其上部桥面板宽1 m部分，采用ABAQUS建立跨度为5 m的三点弯曲梁FEM模型，其中钢梁采用SR4壳单元，其余采用C3D8R体单元，对包含栓钉的混凝土区域进行网格加密，全模型共结点314 033个，单元215 456个，建立参考点，将其与顶部加载块耦合，并建立全局通用接触，设置接触法向与切向接触行为，底部垫块底面约束所有自由度。全局网格划分如图7所示。

图7 FEM模型网格划分

模型包含C50混凝土和Q345钢2种材料，对于钢筋，采用理想弹塑性双线性本构：

(3)

对于剪力钉和钢板，采用三折线弹塑性强化本构：

(4)

式中：Es为钢筋弹模，取2.06×105MPa；fy为钢材屈服强度；εy为屈服应变；fu为钢材极限强度，取fu/fy=1.2；εu为极限应变，取εu/εy=21。

对于混凝土，采用混凝土损伤塑性本构，依据《混凝土结构设计规范GB 50010-2010》[15]给出的混凝土单轴受压应力应变曲线，分别定义材料的受拉和受压行为[图8(a)、 图8(b)]，其余CDP参数如下：φ为35°，ε0为0.1，σb0/σc0为1.16，Kc为0.67，μ为0.005。

(a) 混凝土单轴受拉应力应变

3.3 单部件锈蚀对承载力退化的影响

对上述FEM模型采用位移加载模式，对参考点施加竖直向下位移，在自重作用和顶部加载块位移加载作用考虑如下7种工况:①W1为无锈蚀;②W2为钢筋全圆周非均匀锈蚀;③W3为钢筋上半圆周非均匀锈蚀;④W4为钢筋下半圆周非均匀锈蚀;⑤W5为栓钉全圆周非均匀锈蚀;⑥W6为栓钉顺桥向半圆周非均匀锈蚀;⑦W7为栓钉横桥向半圆周非均匀锈蚀。栓钉锈蚀率按5%计，钢筋锈蚀率按5%计，利用式(10)～式(13)将锈蚀率换算为锈蚀层厚度Δ对模型施加锈胀力。

各工况下三点弯曲梁荷载的位移曲线见图9。

图9 单部件锈蚀工况荷载-位移曲线对比

由图9可知，W2～W7曲线均在W1的下方，说明钢筋和栓钉锈蚀对钢混组合梁承载能力存在削弱作用，W2曲线在W3、W4下方，W5曲线在W6、W7下方，说明全圆周非均匀锈蚀的削弱作用要强于半圆周非均匀锈蚀，而W3、W4和W6、W7曲线较为接近，说明单独对钢筋或栓钉半圆周锈蚀而言，其锈蚀面为上下半圆周或横桥向、顺桥向半圆周对结构承载能力的影响较小。钢筋全圆周非均匀锈蚀工况下，峰值荷载为2 161.6 kN，栓钉全圆周非均匀锈蚀工况下，峰值荷载为2 396.4 kN，以无锈蚀时峰值荷载2 522.7 kN为基准，则2类全圆周非均匀锈蚀工况峰值荷载分别下降了14.3%、5.0%。

3.4 多部件锈蚀对承载力退化的影响

3.3节中对单个部件锈蚀与承载力退化的关系进行了研究，现考虑多部件锈蚀的影响，即将3.3节中工况进行组合，由于多部件锈蚀对结构承载力影响为一非线性效应，故上述各个工况的组合并非简单的线性叠加。考虑到单部件锈蚀工况中W3、W4和W6、W7荷载的位移曲线较为接近，故组合工况分别为：①W2+W5(钢筋、栓钉全圆周非均匀锈蚀)；②W2+W6(钢筋全圆周非均匀锈蚀，栓钉顺桥向半圆周非均匀锈蚀)：③W3+W5(钢筋上半圆周非均匀锈蚀，栓钉全圆周非均匀锈蚀)。

各工况下三点弯曲梁荷载的位移曲线见图10，各工况峰值荷载见表1。

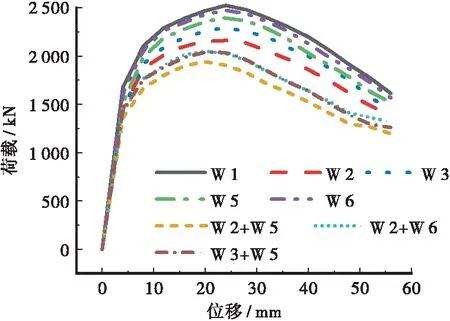
图10 多部件锈蚀工况荷载-位移曲线对比

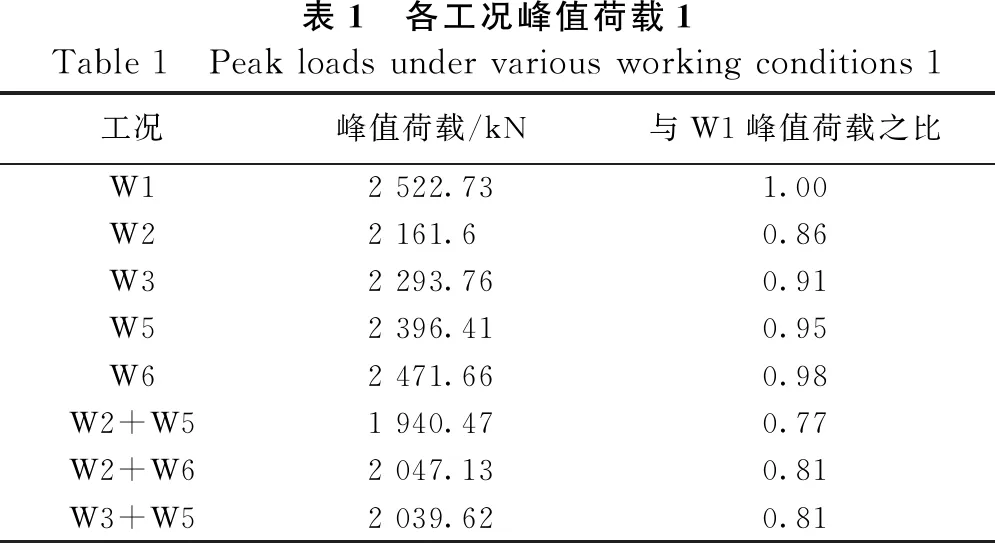
表1 各工况峰值荷载1Table 1 Peak loads under various working conditions 1工况峰值荷载/kN与W1峰值荷载之比W12 522.731.00W22 161.60.86W32 293.760.91W52 396.410.95W62 471.660.98W2+W51 940.470.77 W2+W62 047.130.81 W3+W52 039.620.81

由图10、表1可知，相较于单部件锈蚀工况W2、W3、W5、W6，多部件组合锈蚀工况下峰值荷载进一步降低，其中峰值荷载下降最大工况为W2+W5，1 940.47 kN，下降最小为W2+W6，2 047.13 kN，相较于W1峰值荷载2 522.7 kN，分别降低了23.0%、18.9%，且多部件组合工况下峰值荷载下降幅度要大于单部件工况峰值荷载下降幅度之和，体现了多部件同时发生锈蚀时结构承载力进一步非线性退化的特点。

3.5 锈蚀率的影响

3.3节和3.4节中按5%的锈蚀率对单部件锈蚀、多部件锈蚀下组合梁承载力退化进行了量化分析，现分析钢筋、栓钉在不同锈蚀率1%、2.5%、5%、10%下钢筋、栓钉全圆周非均匀锈蚀时钢混组合梁的承载力退化，工况如下：①G1+S1(钢筋锈蚀率1%，栓钉锈蚀率1%)；②G2+S2(钢筋锈蚀率2.5%，栓钉锈蚀率2.5%)；③G3+S3(钢筋锈蚀率5%，栓钉锈蚀率5%)；④G4+S4(钢筋锈蚀率10%，栓钉锈蚀率10%)；⑤G1+S4(钢筋锈蚀率1%，栓钉锈蚀率10%)；⑥G2+S3(钢筋锈蚀率2.5%，栓钉锈蚀率5%)；⑦G3+S2(钢筋锈蚀率5%，栓钉锈蚀率2.5%)；⑧G4+S1(钢筋锈蚀率10%，栓钉锈蚀率1%)。

注：G1～G4分别表示钢筋不同锈蚀率1%、2.5%、5%、10%的情况，S1～S4分别表示栓钉不同锈蚀率1%、2.5%、5%、10%的情况。

各工况下三点弯曲梁荷载-位移曲线见图11，各工况峰值荷载见表2。

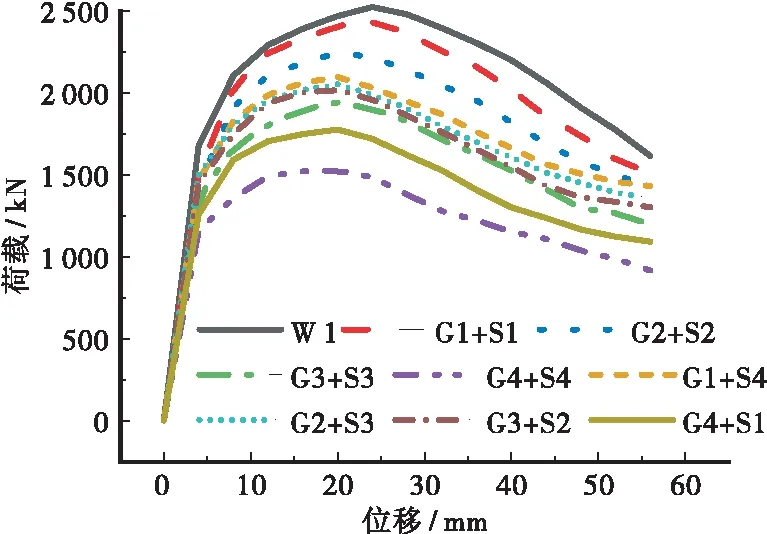
图11 不同锈蚀率多部件锈蚀工况荷载-位移曲线对比

表2 各工况峰值荷载2Table 2 Peak loads under various working conditions 2工况峰值荷载/kN与W1峰值荷载之比W12 522.731.00 G1+S12 428.980.96 G2+S22 244.320.89 G3+S31 940.470.77 G4+S41 526.990.61 G1+S42 095.170.83 G2+S32 052.560.81 G3+S22 015.740.80 G4+S11 775.570.70

由图11、表2可知，相较于无锈蚀的组合梁，各部件发生锈蚀后承载力随锈蚀率不同而发生了相应程度的退化，当钢筋、栓钉锈蚀率相等时，锈蚀率越大峰值荷载越低，其中当钢筋、栓钉锈蚀率均为10%时峰值荷载下降程度最大，相较于W1工况降低约39%；而当钢筋、栓钉锈蚀率不同时，G1+S4工况下(钢筋锈蚀率1%，栓钉锈蚀率10%)峰值荷载为2 095.17 kN，而G4+S1工况下(钢筋锈蚀率10%，栓钉锈蚀率1%)峰值荷载为1 775.57 kN，即钢筋锈蚀对峰值荷载的影响更为显著。

4 结论

本文根据锈胀应力场理论，推导了均匀锈蚀、非均匀锈蚀混凝土保护层应力分量解析表达式，并以此为基础，建立某钢混组合梁桥简化FEM模型，定量分析了钢筋、栓钉在单部件锈蚀、多部件锈蚀情况下的承载力，研究了多部件不同锈蚀率组合对承载力退化的影响，得出以下结论：

a.平面应变FEM模型计算结果与均匀锈蚀、非均匀锈蚀解析解吻合良好，非均匀锈胀力作用下混凝土保护层环向、径向应力分布与均匀锈胀力作用不同，其随角度的分布是正弦函数形式，且峰值更高，约为均匀锈胀力作用下环向、径向应力峰值的1.75倍。

b.建立了全圆周、半圆周非均匀锈蚀下锈蚀率与锈蚀层厚度、钢筋/栓钉有效截面的关系，通过指定锈蚀率可计算锈蚀层厚度、有效截面积，从而实现了FEM模型中对指定锈蚀率下锈胀力的加载。

c.单部件全圆周、半圆周5%锈蚀率下，全圆周非均匀锈蚀工况承载力下降幅度较大，以无锈蚀时峰值荷载2 522.7 kN为基准，则钢筋、栓钉全圆周非均匀锈蚀工况峰值荷载分别下降了14.3%、5.0%；多部件组合锈蚀工况下承载力进一步降低，最大工况W2+W5峰值荷载降低了23.0%，且组合工况下降幅度大于单部件工况下降幅度之和，体现了多部件同时发生锈蚀时结构承载力进一步非线性退化的特点。

d.承载力退化程度与锈蚀率呈正相关，且钢筋锈蚀对结构承载力的影响更为显著。