sl(2,)到其单模V(3)和V(4)的局部导子

李赵鑫, 王淑娟

(黑龙江大学 数学科学学院, 哈尔滨 150080)

自Kadison[1]和Larson等[2]引入局部导子的概念以及Crist[3]研究了算子代数的局部导子以来, 关于局部导子的结构和性质研究得到广泛关注[4-8]. Ayupov等[9-10]证明了特征零代数闭域上的非交换Arens代数与半单李代数到伴随模的局部导子都是导子. 但对于可解李代数的局部导子结论相对复杂, 既存在一族可解李代数具有非导子的局部导子, 也存在一族可解李代数的局部导子都是导子的结论[11].

本文将李代数到伴随模的局部导子的概念推广到李代数到任意有限维模, 并且决定了A型单李代数sl(2,)到其两类单模的局部导子空间.sl(2,)是一类很重要的单李代数, 其表示理论决定了半单李代数的结构.本文将sl(2,)到其任意单模V(n)的局部导子问题等价地转化为线性方程组求解, 进而转化为系数矩阵与增广矩阵的秩恒等, 得到了sl(2,)到V(4)的局部导子都是导子,sl(2,)到V(3)有非导子的局部导子的结论.

1 预备知识

本文约定L为复数域上的有限维李代数,V为有限维L-模.令Hom(L,V)表示L到V的线性映射全体.

定义1设D∈Hom(L,V), 若

D([x,y])=xD(y)-yD(x), ∀x,y∈L,

则称D是L到V的导子.

令Der(L,V)为L到V的导子全体.易证明Der(L,V)为有限维向量空间.

定义2设Δ∈Hom(L,V), 若对于任意x∈L, 均存在与x有关的D∈Der(L,V), 使得Δ(x)=D(x), 则称Δ为L到V的局部导子.

令Lder(L,V)为L到V的局部导子全体.易证明Lder(L,V)为有限维向量空间.

定义3设D∈Hom(L,V), 若存在v∈V, 使得对于任意x∈L, 均有D(x)=xv, 则称D为由v决定的内导子, 将其记为Dv.易知Dv∈Der(L,V).

令Ider(L,V)={Dv|v∈V}.易证明Ider(L,V)为有限维向量空间, 且

Ider(L,V)≤Der(L,V)≤Lder(L,V)≤Hom(L,V).

考虑迹为0的线性变换组成的特殊线性李代数sl(2,), 具有标准基e,h,f.则sl(2,)的(n+1)维单模V(n)具有标准基v0,v1,…,vn, 其模作用为

evi=i(n+1-i)vi-1,hvi=(n-2i)vi,fvi=vi+1,

其中i=0,1,…,n,v-1=vn+1=0.于是关于有序基v0,v1,…,vn,sl(2,)中每个元素均对应一个矩阵.为方便, 引入矩阵E,H,F, 使得

引理1[12]设x=xee+xhh+xff∈sl(2,){0}, 其中xe,xh,xf∈.令

(xv0,xv1,…,xvn)=(v0,v1,…,vn)X.

则X=xeE+xhH+xfF, 且:

1) 当n为偶数时, rankX=n;

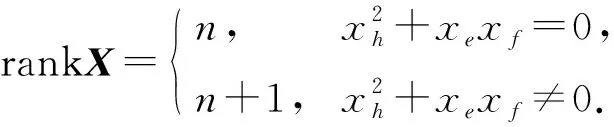
引理1确定了sl(2,)中任意元素对应矩阵的秩.

2 局部导子

令VL={v∈V|xv=0, ∀x∈L}.

引理2若V为非平凡的单L-模, 则

a1Dv1+a2Dv2+…+akDvk=0 ⟺a1v1+a2v2+…+akvk=0,

其中v1,v2,…,vk∈V,a1,a2,…,ak∈.特别地,v1,v2,…,vk为V的基 ⟺Dv1,Dv2,…,Dvk为Ider(L,V)的基.

证明: 任取x∈L, 则

即a1Dv1+a2Dv2+…+akDvk=Da1v1+a2v2+…+akvk.于是充分性显然成立.下面证明必要性.

设a1Dv1+a2Dv2+…+akDvk=0.对于任意的x∈L, 则

(a1Dv1+a2Dv2+…+akDvk)(x)=0,

从而

Da1v1+a2v2+…+akvk(x)=x(a1v1+a2v2+…+akvk),

于是a1v1+a2v2+…+akvk∈VL.注意到VL为V的平凡子模, 而V为非平凡的单模, 故VL=0, 进而

a1v1+a2v2+…+akvk=0.

证毕.

由引理2可知, Ider(sl(2,),V(n))具有基Dv0,Dv1,…,Dvn.此外, 由于sl(2,)到V(n)具有平凡的一阶上同调, 故sl(2,)到V(n)的导子均是内导子.于是Der(sl(2,),V(n))具有基Dv0,Dv1,…,Dvn.本文约定eij表示第i行第j列位置为1、 其余位置为0的(n+1)×3阶矩阵单位.为方便, 对于0≤i≤n, 引入矩阵Di, 使得

(Dvi(e)Dvi(h)Dvi(f))=(v0v1…vn)Di.

由于Dvi(x)=xvi, 则

D0=ne12+e23,Dn=nen1-nen+1,2,Dj=j(n+1-j)ej1+(n-2j)ej+1,2+ej+2,3,

其中1≤j≤n-1.注意到Hom(sl(2,),V(n))中每个元素φ关于有序基e,h,f和v0,v1,…,vn都对应一个(n+1)×3矩阵, 于是可设

(φ(e)φ(h)φ(f))=(v0v1…vn)Φ.

若φ∈Der(sl(2,),V(n))或Lder(sl(2,),V(n)), 则称矩阵Φ分别为sl(2,)到V(n)的导子或局部导子.

下面将局部导子的求解问题等价地转化为相关矩阵秩恒等的问题.

引理3设Φ是(n+1)×3矩阵, 则Φ∈Lder(sl(2,),V(n))的充要条件是对任意的y∈3, 恒有

rankM=rank(MΦy),

其中M=(D0yD1y…Dny).

证明: 设φ∈Hom(sl(2,),V(n))关于有序基e,h,f和v0,v1,…,vn对应的矩阵为Φ, 则Φ∈Lder(sl(2,),V(n))等价于对任意的x∈sl(2,), 均存在与x有关的a0,a1,…,an∈, 使得

φ(x)=(a0Dv0+a1Dv1+…+anDvn)(x).

(1)

令x=xee+xhh+xff,y=(xe,xh,xf)T.一方面, 有

φ(x)=φ(xee+xhh+xff)=(φ(e)φ(h)φ(f))y=(v0v1…vn)Φy;

另一方面, 有

aiDvi(x)=aiDvi(xee+xhh+xff)=ai(Dvi(e)Dvi(h)Dvi(f))y=ai(v0v1…vn)Diy.

由式(1)知

(a0D0+a1D1+…+anDn)y=Φy,

即

(D0yD1y…Dny)(a0,a1,…,an)T=Φy,

从而

M(a0,a1,…,an)T=Φy.

(2)

故Φ∈Lder(sl(2,),V(n))⟺对任意xe,xh,xf∈, 关于a0,…,an的线性方程组(2)有解⟺对任意y∈3, rankM=rank(MΦy)恒成立.证毕.

为方便, 引入一类(n+1)×3矩阵:

下面给出本文的主要结果:sl(2,)到V(3)的所有局部导子.

定理1Lder(sl(2,),V(3))具有基D0,D1,D2,D3,B1,B2, 即存在sl(2,)到V(3)的局部导子不是导子.

证明: 显然D0,D1,D2,D3,B1,B2线性无关, 且每个Di均为局部导子.下面说明每个Bi均为局部导子, 即证明对任意的y∈3, 恒有

rankM=rank(MBiy),

(3)

其中M沿用引理3中的记号.根据Di的定义可知,Di的第一列为Dvi(e)在有序基v0,v1,…,vn下的坐标.又由于Dvi(e)=evi, 于是Di的第一列为E的第(i+1)列.同理,Di的第二列为H的第(i+1)列,Di的第三列为F的第(i+1)列.设y=(xe,xh,xf)T, 于是M的第(i+1)列为xeE+xhH+xfF的第(i+1)列, 从而

M=xeE+xhH+xfF,

进而

下面分两种情形证明式(3).

rank(MBiy)=3,i=1,2,

于是式(3)成立.下面设xexf≠0, 此时必有xh≠0.将(MB1y)的第一行依次与第二行、 第三行、 第四行交换, 再利用xf将其化为行阶梯型, 得

同理将(MB2y)化为阶梯型, 得

故对于B1,B2均有式(3)成立.

任取φ∈Lder(sl(2,),V(3))， 设φ关于有序基e,h,f和v0,v1,v2,v3对应的矩阵为Φ.下面证明Φ为D0,D1,D2,D3,B1,B2的线性组合.不妨设则

① 取xh=xe=0,xf≠0, 则f0=0;

② 取xh=xf=0,xe≠0, 则e3=0;

其中

故

由xh,xf的任意性可知,

h0-3f1=0, -e0-3h1+6f2=0, -6e2-6h3=0, 3e1+6h2-6f3=0.

综合①～③可知

证毕.

下面给出本文的另一个主要结果,sl(2,)到V(4)的所有局部导子.

定理2Lder(sl(2,),V(4))具有基D0,D1,D2,D3,D4, 即sl(2,)到V(4)的局部导子均为导子.

证明: 显然D0,D1,D2,D3,D4线性无关, 且每个Di均为局部导子.下面说明Lder(sl(2,),V(4))的任意元素φ均为D0,D1,D2,D3,D4的线性组合.仍沿用上述符号M,y,Φ, 则

从而有以下结论：

① 取xh=xe=0,xf≠0, 则f0=0;

② 取xh=xf=0,xe≠0, 则e4=0;

③ 取xe=xf=0,xh≠0, 则h2=0;

其中

故

由xh,xe,xf的任意性知,

-4f1+h0=0, -4f2+e0=0, 24h3+8e2=0, -4e1+24f3=0,

-4e2+24f4=0, -4h1+8f2=0, 24e3+24h4=0.

综合①～④可知

证毕.