一类四阶非线性发展方程的整体吸引子
杨佳雪, 段 宁
(东北大学 理学院, 沈阳 110004)
1 引言与主要结果
在研究动力学控制晶体生长过程中小平面和角点的形成时, Golovin等[1]引入了如下四阶非线性发展方程:

(1)
该方程可用于刻画无表面生长时取向不稳定的晶体表面, 其中线性阻尼系数v>0描述了边缘附加能量的稳定作用, 且决定边缘的宽度, 系数m>0表征了热力学不稳定表面线性刻画的不稳定性, 正常数a,b,c是表征小平面稳定取向的系数.
Duan等[2]将方程(1)简化为如下的一维形式:

(2)
并为方程赋予了Neumann边值条件和初值条件, 考虑了其整体弱解的存在唯一性, 证明了当初值u0(x)∈Hk(0,1)(k∈(0,+∞))时, 方程(2)在Hk(0,1)空间存在一个整体吸引子.本文进一步研究方程(2)解的长时间行为.考虑到实际的物理背景, 对于u和阶数≤3的u的导数附加如下周期边值条件[3]:
φ|xi=0=φ|xi=li,i=1,2,3,
(3)
且假设方程的初值条件为
u(x,0)=u0(x),x∈(0,1).
(4)
本文仅假设初值所在的空间为H1(0,1), 证明方程(2)在更高阶空间H4(0,1)中存在整体吸引子.本文结果对初值正则性的要求较低, 因此可视为是对Duan等[2]结果的改进.
首先, 问题(2)-(4)的解满足质量守恒, 即
进一步, 可给出整体弱解的存在性:
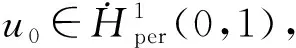

下面给出本文的主要结果.
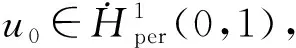
2 解的一致估计

引理2假设u0∈L2(0,1), 并且v充分大, 则
‖u(t)‖≤M0, ∀t≥T0,

其中M0是依赖m,a,v的正常数,T0是依赖m,a,v和R的正常数.
下面涉及的正常数Mi和Ti(i=1,2,…,6)均具有与M0和T0相同的要求.
证明: 将方程(2)两边同乘u, 并在(0,1)上积分, 可得

(5)
因为
所以有

(6)
利用质量守恒和Poincaré不等式[5], 可得
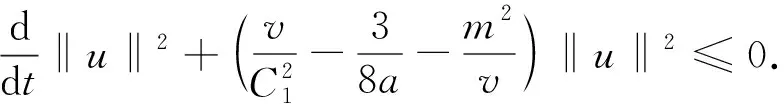
(7)


(8)


(9)
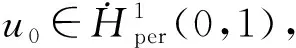
‖ux(t)‖≤M1, ∀t≥T1,

证明: 将方程(2)两边同乘-uxx, 并在(0,1)上积分, 可得
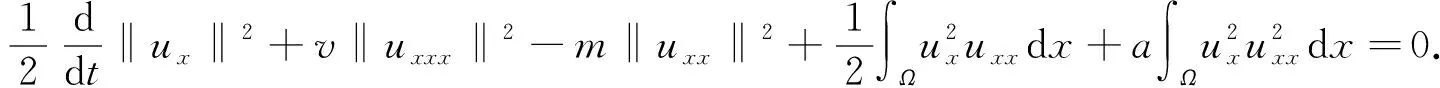
(10)
因为
所以有

(11)
从而有

(12)
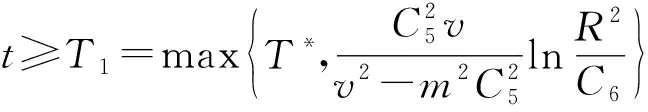

(13)
由积分中值定理知, 存在一个时间t0∈(T1,T1+1), 使得‖uxxx(t0)‖2≤C8.
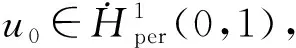
‖uxx(t)‖≤M2, ∀t≥T2,

证明: 将方程(2)两边同乘uxxxx, 并在(0,1)上积分, 可得
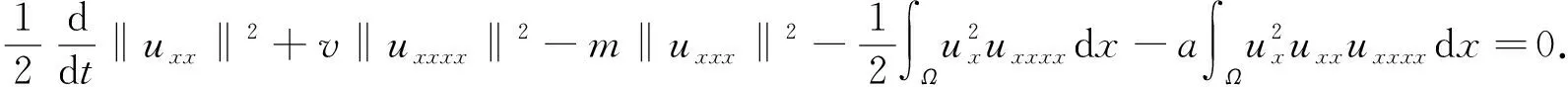
(14)
因为
所以由Nirenberg不等式知
整理得

(15)

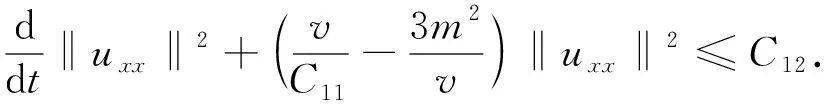
(16)
由Gronwall不等式知
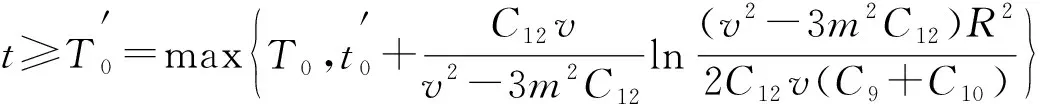
‖uxx(t+1)‖2≤C13+‖uxx(s)‖2.
(18)
在(t,t+1)上, 对式(18)中s积分再结合式(9), 可得

(19)
由Sobolev嵌入定理[7]、 引理2、 引理3和式(19)可得‖ux‖∞≤C15.
将方程(2)两边同乘ut, 并在(0,1)上积分, 可得
所以有

(21)
将式(21)在(t+1,t+2)积分, 并结合引理2、 引理3和式(17)有
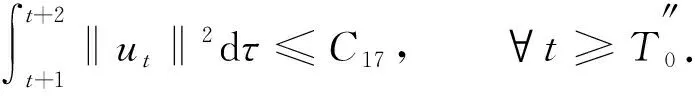
(22)
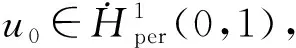
‖uxxx(t)‖≤M3, ∀t≥T3,

证明: 对方程(2)关于x求二阶导, 得

(23)
将方程(23)两边同乘uxxxx, 并在(0,1)上积分, 可得

(24)
由Nirenberg不等式可知
所以有
综上, 有
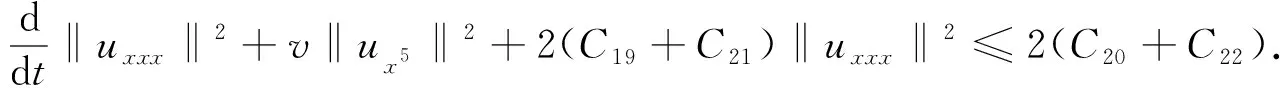
(25)
由Gronwall不等式, 得

‖uxx‖∞≤C23.
将方程(23)两边同乘ut, 并在(0,1)上积分, 可得
整理得

(26)
令t≥T1*,s∈(t,t+1), 在(s,t+1)上对式(26)积分, 可得
v‖uxxx(t+1)‖2≤C24+v‖uxxx(s)‖2+m‖uxx(t+1)‖2-m‖uxx(s)‖2,
对s积分, 有

(27)

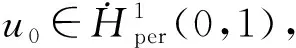
证明: 令w=ut, 将方程(2)对t微分, 得

(28)
注意到
‖wx‖≤‖w‖2/3‖wxxx‖1/3, ‖wxx‖≤‖w‖1/3‖wxxx‖2/3.
将方程(28)两边同乘w, 并在(0,1)上积分, 可得
即

(29)
由Poincaré不等式和质量守恒知


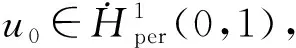
证明: 将方程(28)两边同乘Aw, 并在(0,1)上积分, 可得
由Poincaré不等式和质量守恒知
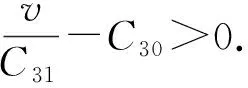
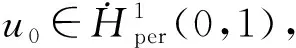
证明: 由方程(2)、 引理2~引理7, 可知∀t≥T6=max{T1,T2,…,T5}, 有
证毕.
3 定理1的证明
考虑问题(2)-(4), 首先证明{S(t)}t≥0存在一个(H1,H1)整体吸引子; 其次证明该吸引子也是问题(2)-(4)的一个(H1,H4)吸引子.
假设M1和M6分别是引理3和引理8中的常数, 且
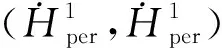
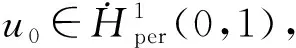
证明: 由方程(2)可知

‖wn‖D(A1/2)≤M5, ‖un‖D(A2)≤M6, ∀t≥T,n=1,2,….
(31)
因为tn→∞, 故存在N>0, 使得对于所有的n≥N, 均有tn≥T成立.因此, 由式(31)可得
‖wn(tn)‖D(A1/2)≤M5, ‖un(tn)‖D(A2)≤M6, ∀n≥N.
(32)

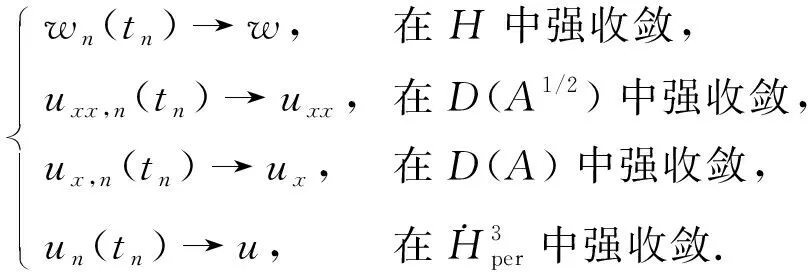
(33)
由式(31)和Sobolev嵌入定理, 可得‖un(tn)‖L∞≤C, ∀n≥N.从而可得
‖wn(tn)-w‖2→0, ‖un(tn)-u‖2→0, ‖uxx,n(tn)-uxx‖2→0,
并且有