F1格范畴的表现定理
张立国
(沈阳理工大学 理学院,辽宁 沈阳 110159)
0 引言
完全分配格是经典格论的重要研究对象,对其结构的讨论一直是热点问题.无论是连续的DCPO理论[1-5],还是Fuzzy拓扑学都对其做出过相关的研究[6-9].超分子作为完全分配格的刻划工具,文献[1]对超分子集SM(L)的结构进行讨论,发现当完全分配格的每个元素都具有唯一的极小集时,它的分子集M(L)的序是离散的.本文在此基础上研究这类完全分配格(即F1格)性质,构造F1格范畴CD*,讨论该范畴对象的结构与态射的性质,并证明它的表现定理,为连续格理论和Fuzzy拓扑学的后续研究奠定基础.
1 预备知识
设L是完全分配格,M(L)表示L的分子集.若a∈L,以β(a)表示a的最大极小集,β*(a)=β(a)∩M(L).可以证明a是分子当且仅当β*(a)是定向集.众所周知L是完全分配格,则M(L)是连续的DCPO.
2 范畴CD*的结构与性质
定义1 设L是完全分配格,若L的每个元素都有唯一的极小集,称L为F1格.
定义2[8]设L1,L2是完全分配格,映射f:L1→L2被称为广义序同态.如果f满足如下条件:
1)f(a)=0当且仅当a=0;
2)f有保并的右伴随.
定义3 以F1格为对象,以广义序同态为态射的范畴,称为F1格范畴,记作CD*.
命题1 设L为F1格,则M(L)的序是离散的,从而β*(a)={a}(其中a∈M(L))
证明只需证,若a、b∈M(L),且a≠b,则a与b不可比.
由于b∈M(L),则∀x∈β*(b),必有∨[β*(b)
若a
同理可证a≥/b,即a与b不可比,从而β*(a)={a}.
命题2 设L为F1格,则L≅2M(L).
证明设f是L到2M(L)的映射,即∀a∈L,f(a)=β*(a).由L的性质可知,f是映射,故只需证明f为同构映射.
若a、b∈L,且a≠b时,则β*(a)≠β*(b),从而f(a)≠f(b),即f为单射.
若A∈2M(L),则∨A∈L,从而f(∨A)=A.事实上,x∈A,则∨A>x.由前面证明可知x∈β*(∨A)=f(∨A),从而A⊆β*(∨A)=f(∨A),因此A是∨A的极小集.由于∨A有唯一的极小集,所以A=β*(∨A)=f(∨A),即f为满射.
若a、b∈L,且a 综上所述,L≅2X. 由命题1和命题2可得如下结论. 命题3 设L为F1格,则存在集合X使得L≅2X,且|M(L)|=|X|. 任给集合X,令2X={A|A⊆X}.按包含序2X是偏序集.由于其满足完全分配律,故2X为完全分配格,分子集为M(2X)={{x}|x∈X}.而2X的每个元素A都有唯一的极小集{{x}|x∈A},因此2X为F1格.显然有如下结论. 命题4 设X为集合,则2X是F1格,且X≅M(2X). 定义4 以集合X为对象,以单射为态射的范畴,称为集合范畴,记作Set*. 命题5 设L1、L2是F1格,若f:L1→L2是广义序同态,则T(f)=f|M(L1):M(L1)→M(L2)为单射(其中f把分子映射成分子). 证明设a∈M(L1),f(a)≤b∨c,则a≤g(b∨c)=g(b)∨g(c)(其中g为f的右伴随),从而a≤g(b)或a≤g(c),因此f(a)≤b或f(a)≤c.由于a≠0,可知f(a)≠0,所以f(a)∈M(L2),所以f(a)∈M(L2). 若x、y∈M(L1),f(x)≠f(y),则f(x)∧(y)=f(x∧y)=0.由于f是广义序同态,因而x∧y=0,从而x≠y,因此f为单射. 命题6 设L1、L2是F1格,若f:M(L1)→M(L2)是单射,若a∈L1,令L(f)(a)=∨L2{f(x)|x∈M(L1),且x≤a},则L(f):L1→L2是广义序同态,且L(f)|M(L1)=f. 证明(1)设a、b∈L1,a≤b.若x∈M(L1),x≤a,则x≤b,因而{f(x)|x∈M(L1),且x≤a}⊆{f(x)|x∈M(L1),且x≤b},从而∨L2{f(x)|x∈M(L1),且x≤a}≤∨L2{f(x)|x∈M(L1),且x≤b,即L(f)(a)≤L(f)(b),故L(f)为序同态. (2)设a、b∈L1,a≠b,则{x∈M(L1)|x≤a}≠{x∈M(L1)|x≤b}.由于f为单射,故{f(x)∈M(L2)|x≤a}≠{f(x)∈M(L2)|x≤b}.据命题1可知,∨L2{f(x)∈M(L2)|x≤a}≠∨L2{f(x)∈M(L2)|x≤b},即L(f)(a)≠L(f)(b),从而L(f)为单射,因此L(f)(a)=0当且仅当a=0. (3)令L(f)*(b)=∨L1{y∈M(L1)|f(y)≤b}.若L(f)(a)≤b,则∀x∈M(L1)且x≤a,都有f(x)≤b,从而x∈{y∈M(L1)|f(y)≤b},因而x≤L(f)*(b),故a≤L(f)*(b).反之,若a≤L(f)*(b),据L(f)的保序性可得L(f)(a)≤b.故L(f)*是L(f)的右伴随. (4)设L(f)*为L(f)的右伴随. (5)若a∈M(L1),据命题1可知,{x|x∈M(L1),且x≤a}={a},因而∨L2{f(x)|x∈M(L1),且x≤a}=f(a),因此L(f)|M(L1)(a)=f(a). 综上所述,L(f)为广义序同态,且L(f)|M(L1)=f. 命题7 设X、Y为集合,若f:X→Y是单射,若A⊆X,令L(f)(A)={f(x)|x∈A},则L(f):2X→2Y是广义序同态,且L(f)|X=f. 证明由命题3和命题6可证. 设L是F1格,令T(L)=M(L),由命题1可知,M(L)∈ob(Set*).设f:L1→L2是广义序同态,令T(f)=f|M(L1),已经证明f为广义序同态当且仅当T(f)为单射,所以T是从范畴CD*到范畴Set*的函子. 设X是集合,令E(X)=2X,由命题3可知,2X∈ob(CD*).设f:X→Y是单射,令E(f)=L(f):2X→2Y,即E(f)(A)=∪{f(x)|x∈A}(A∈2X),已经证明E(f)广义序同态当且仅当f为单射,所以E是从范畴Set*到范畴CD*的函子. 定理1 函子T是完全忠实函子. (2)任取h∈HomSet*(T(L1),T(L2)),由命题5可知存在L(h)∈HomCD*((L1,L2)),使得TL(h)=h,所以T为完全函子 定理2 函子E是完全忠实函子. 命题8[10]设C和D是范畴,F:C→D是函子,则下列条件等价: (1)范畴C和D等价; (2)函子F是完全忠实函子,并且任取B∈ob(D),都存在A∈ob(C),使得F(A)≅B. F1格范畴CD*的表现定理: 定理3 范畴CD*与范畴Set*等价. 证明由命题3、定理1和命题8可证. F1格是每个元素都有唯一的极小集的完全分配格,其结构相对简单.结合本文取得结论可以看到,F1格实为建立在经典集合上的幂集格(按包含序),而其上的广义序同态与经典集合之间单射相对应等.这为从集合论的角度研究完全分配格提供新想法,也带来新问题. 问题F1格上的广义序同态是否为经典集合之间单射所诱导.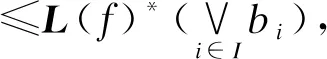
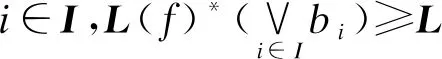
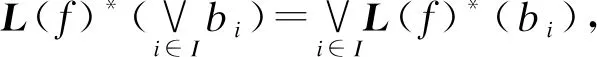
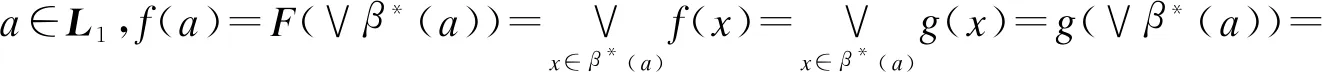
3 结束语

