基于ARIMA 模型的美元汇率预测

蒋 奇，刘永文

（贵州大学经济学院，贵阳 550025）

汇率的预测准确度对外汇的持有者、依赖进出口贸易的企业、个人和企业的外汇交易行为等都有很大的影响。在科技不断发展、统计分析技术不断提高的背景下，时间序列模型被广泛应用于经济领域中。基于时间序列模型，在短期内可以很好拟合真实值，因此时间序列模型经常被用来预测短期的数据走势。

一、模型的理论

（一）AR（p）模型

如果一个时间序列{X}的当前值与过去p 个时刻的序列值之间的关系是线性的，即可以用过去p个时刻的序列值来表示，则称这个线性过程为{X}的p 阶自回归方程用AR（p）表示。AR（p）模型的一般形式为：

其中，φ 为自回归系数，p 为阶数，ε为白噪声序列，满足零期望E（ε）=0，同方差Var（ε）=σε，且无自相关Cov（ε，ε）=0，t≠s。

与自回归模型常联系在一起的是平稳性问题，自回归的特征方程为：

如果特征方程的所有根的绝对值都大于1，则AR（p）是一个平稳的随机过程。由此，p 阶自回归序列的平稳性条件为：

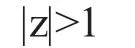
（二）MA（q）模型

如果序列{X}的当前值可以用现在干扰值和过去q阶干扰值线性表示，则称为q 阶移动平均过程MA（q）模型。MA（q）模型的一般形式为：

其中，θ 为回归系数，{ε}为白噪声序列。

MA（q）的特征方程为：

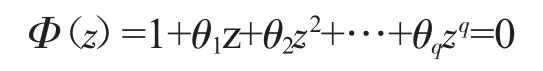
如果这个特征方程的全部根绝对值都大于1，即|z|＞1，这个条件成为移动平均过程的可逆性条件。

（三）ARIMA 模型

ARIMA 模型又称自回归积分移动平均模型，当时间序列本身不是平稳的时，考虑其差分ΔX=X-X=（1-L）X，可以将{X}看成是平稳的序列。

ARIMA（p，d，q）模型表示为：

以上模型就是最简单的ARIMA 模型，可视为经过d 阶差分后再把AR（p）和MA（q）两个模型综合而成。

二、实证分析

本文数据均选自于国家外汇管理局2020 年8 月20 日至2020 年12 月31 日的91 个日数据。

（一）平稳性检验

首先，我们对原序列进行ADF 检验，结果如表1。可以看出，原时间序列的t 统计量均大于1%、5%、10%水平下的临界值，因此，原时间序列为不平稳序列。

表1 原时间序列ADF检验结果

ARIMA 模型要求时间序列必须为平稳的时间序列，我们要运用差分的方法对原始数据进行处理。依然对差分后的序列进行ADF 检验，结果如表2。可以看出，差分后的时间序列的t 统计量均小于1%、5%、10%水平下的临界值，因此，差分后的时间序列为平稳序列。

表2 差分后时间序列的ADF结果

（二）模型识别

原数列经过一阶差分后，变成了平稳的时间序列，我们运用python 画出一阶差分序列的自相关图和偏自相关图（见图1）。

图1 自相关图（上）和偏自相关图（下）

具体的阶数我们要运用AIC 准则。我们必须知道，自由参数的种类越多，模型拟合的质量就会越优；AIC既要充分考虑到数据拟合的质量优劣性，又必须要有效地避免过分拟合。因而首先选择的模型必须是AIC值最小的。

本文使用python 中的pmdarima 库中auto_arima函数，由函数自动为我们推荐最优的预测模型。我们可以从表3 得出，AIC 值最低的是模型ARIMA（2，1，2），因此最好的模型为ARIMA（2，1，2）。

表3 模型阶数和对应的AIC值

运用ARIMA（2，1，2）模型进行参数估计，分别得出了自回归系数和移动平均系数（见表4）。

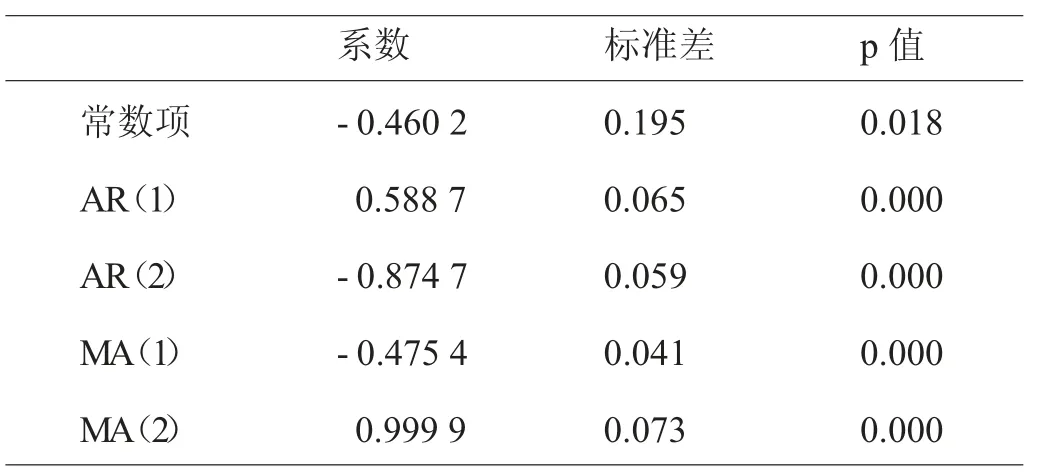
表4 参数估计结果

由表3 可以看出，常数项的p 值为0.018，在5%的水平下显著；AR（1）、AR（2）、MA（1）、MA（2）对应的p值均为0，均为显著性变量。因此我们建立的模型为：

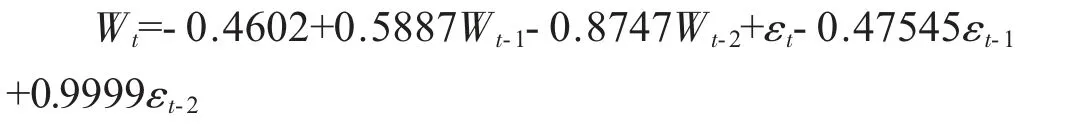
（三）残差检验

模型建立好后，需要进行残差相关性和拟合性检验，结果如图2。

由图2 可知，残差分布接近于正态分布，Q 检验接近于对角线，说明我们选取的模型拟合的较好，可以进行预测。

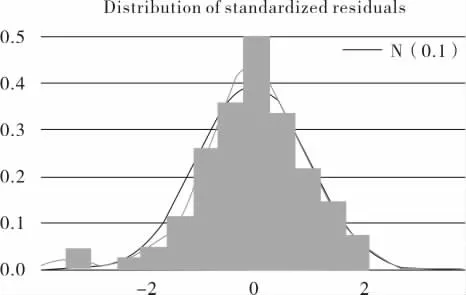
图2 残差直方密度分布（上）和残差Q检验（下）

如图3 所示，对时间序列的LB 检验可知，p 值均在0.05 以上，因此时间序列为白噪声序列。

（四）结果预测

使用ARIMA（2，1，2）模型对2020 年12 月18 日至12 月31 日的汇率进行预测，结果如表5。

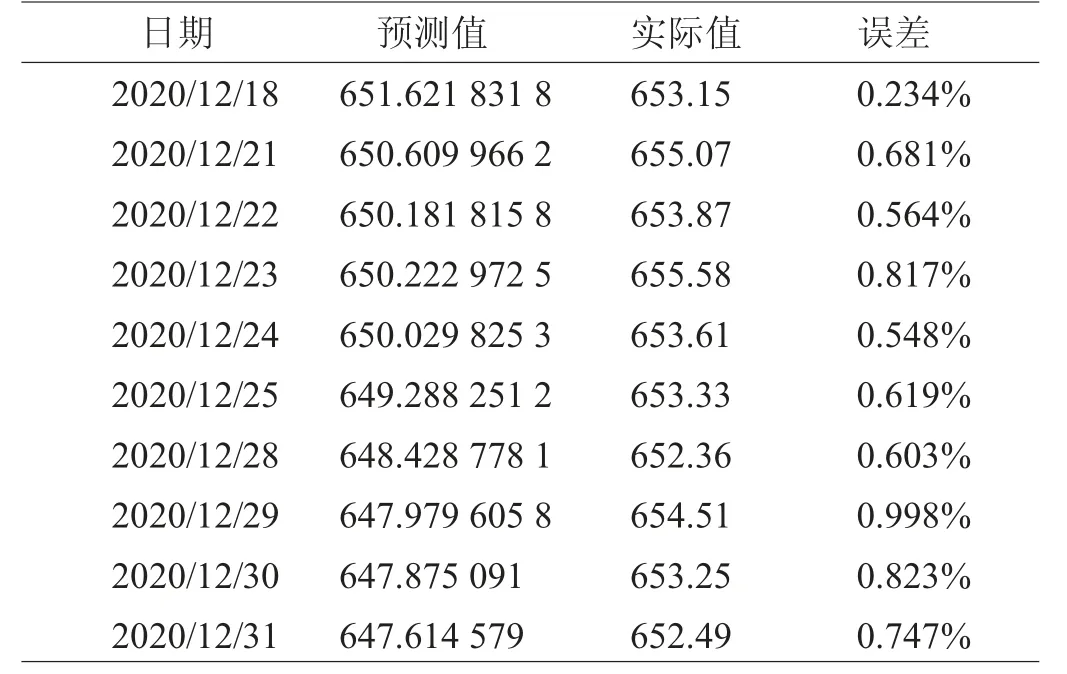
表5 模型预测结果

由表5 可以看出，模型预测值与实际值的误差均在1%以内，说明我们的模型拟合比较准确；再者，我们从表4 中可以看出，尽管误差均在1%以内，但是前五个工作日的误差均值为0.569%，后五个工作日的误差均值为0.758%，说明ARIMA 模型短期内预测误差偏小、长期预测误差偏大。

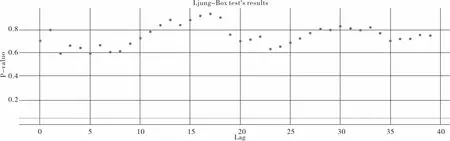
图3 LB检验

结语

时间序列模型是根据历史数据的波动特征来预测未来趋势的一种方法，这种方法要求数据必须是平稳的，对不平稳的数据可以采用差分或者对数差分来使数据平稳化。时间序列模型在金融领域上的应用十分广泛，这得益于它更加简便快捷，不需要太多的变量来刻画原始数据的特征。建模过程中，p 和q 的阶数是至关重要的，它们直接决定着最后预测的准确性。利用python中的pmdarima 库中auto_arima 函数就可以避免产生这个问题。auto_arima 函数可以直接给你提供最适合的阶数，本文的结论也验证了auto_arima 函数推荐的模型预测很准确。用时间序列模型对汇率进行短期预测，有利于进出口企业的贸易开展，也能为国际投资者提供投资依据。