考虑信息的企业合作动机研究——基于序贯博弈

崔思雯

（贵州大学经济学院，贵阳 550025）

引言

在社会发展的进程中，合作无处不在。商业环境下，企业合作有利于企业的创新行为及企业间的资源共享；企业合作能够拓宽单一企业的生产经营模式，通过合作帮助企业提供新的生产经营思路，实现更大利益。但基于合作形式的多样性，企业之间就什么方面产生合作，在合作过程中会面临什么挑战都是需要考虑的问题。面对现有的合作机遇和合作困境，如何进一步实现合作升级，从而创造更大的价值？

企业之间为达成合作协议，实现资源或信息的共享是需要花费成本的。企业为在合作时取得更多的谈判筹码，会尽可能多地去获取对方企业的信息，但过多的信息会造成信息拥堵，进而导致信息浪费，同时企业还需要为储存这些信息而花费更多成本，那么应该获取多少信息才是最佳状态？企业会选择为合作行为花费多少信息成本？

本文将市场上的企业简化为两种，即领导企业与跟随企业，并运用Stackelberg 模型进行序贯博弈分析，探讨两种企业之间在存在信息成本的情况下会如何进行合作决策。

一、文献综述

企业合作问题及不完全信息博弈问题一直以来受到国内外学界的广泛关注，国内外许多学者从宏微观角度对企业合作问题进行了大量理论或实证研究，本文主要参考其中企业合作及不完全信息博弈方面的文献。

首先，许多学者的研究引入不同的指标、基于不同研究对象，从不同角度来测算企业合作行为。例如，周晓晗、张江华、徐进（2021）基于序贯博弈研究了企业的研发合作动机，以溢出效应作为中心变量，在序贯博弈中，得到在溢出系数处于较低范围内时，领导企业和跟随企业才会建立研发合作。李婧、朱莹婷（2021）研究股权结构对于上市家族企业合作行为的影响，发现股权集中度对家族企业的影响存在一个边界，当股权集中度在该边界之下时，随着股权集中度的增加能够促进家族企业的合作行为，当突破该边界时则产生反向作用。刘宗沅、骆温平（2021）的研究认为，合作绩效对于合作演变产生重要的驱动力，即合作所能带来的收益是合作双方的重点考虑因素。杨珍增、郭晓翔（2021）从反方向进行探究，通过考察合作研发对于合作绩效的影响，发现合作研发对企业出口规模和出口选择有促进作用，且不同的合作对象所产生的促进作用存在明显差异。

其次，针对信息不对称问题，薛凤、陈光宇等（2021）研究两个寡头企业在成本信息不对称情况下的价格歧视问题，发现当寡头垄断企业采用较高成本时，它会倾向于隐藏自身成本信息，因为此时它虽具有信息优势，但也伴随着成本劣势。王君美、王巧玲等（2020）研究了单纯企业创新向外部转让先进技术的契约优化问题，发现信息不对称所带来的技术创新应用创造的利润空间由授权各方共享。彭运芳（2004）将寡头垄断竞争市场的Cournot 模型和Stackelberg 模型进行比较，验证了信息多的博弈方并不一定获益多这个事实。

与本文观点最接近的文献是周晓晗的研究。两者的区别主要体现在：周晓晗的研究基于序贯博弈，以溢出效应作为中心变量探讨溢出水平对于企业研发合作的影响；本文在序贯博弈的基础上，增加信息因素，从信息充分度的角度考虑企业合作的决策行为。

综上所述，虽然大多数学者已经从较多角度选取了不同指标对企业合作进行了讨论，但是大部分研究是基于序贯博弈而未考虑信息不对称问题，或者讨论信息不对称问题而没有考虑决策顺序，即博弈顺序与信息不对称的研究是分离的。本文将这两个研究角度结合起来，利用Stackelberg 模型，在对企业的生产成本的表达中加入对信息成本的考虑，分析信息对于跟随企业跟随行为的影响，体现信息在博弈过程中的重要性。本文的博弈分析主要分为三步：第一步在加入信息成本的条件下确定领导企业和跟随企业的产量；第二步求取企业在合作与不合作两种情况下的对应最优产量；第三步求取企业在选择合作的情况下所对应的信息成本所占总成本的比重。

二、模型构建

（一）模型的基本描述

假设市场上有两个厂商i=1，2 参与竞争，它们生产相同的产品，各自产量为q，故市场上的总产量为Q=q+q，企业j 的反需求函数为p=a-Q，a＞0 表示企业j 的市场容量，企业j 的固定成本为f，边际成本为c。在不完全信息的情况下，企业自身为经营会投入一定的信息成本x，除此之外，竞争企业所投入的信息成本会让企业自身存在“信息搭便车”现象，即获取到对手企业的信息能够帮助自身企业减少一定的生产成本。则企业j 的成本函数为：

其中，0≤θ≤1，θ越接近于0，则表明信息越不充分，θ 越接近与1，表明信息越充分。

假设企业1 为市场上的领导企业，企业2 为市场上的跟随企业。企业j 的利润函数为：

上式中第一项（a-q-q）q表示企业j 的销售收入，第二项Cq表示企业j 的总生产成本。

企业1 与企业2 之间是一个不完全信息动态博弈过程，该博弈过程基于Stackelberg 模型，包括三个阶段：阶段一，求取企业1 与企业2 的均衡产量；阶段二，求取企业1 和企业2 在合作与不合作两种情况下所投入的信息成本；阶段三，企业决策，判断企业是否选择进行合作。定义企业之间不合作为N，合作为Y。

（二）模型求解

1.基于Stackelberg 模型的产量均衡

将（10）式和（11）式分别代入（8）式和（9）式，得到

3.企业决策

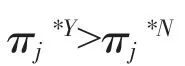
为简化计算过程，对相应参数进行赋值：由于企业应在市场上有利可图才会进行生产，故市场容量应相对较大，这里令a=5。规模大的企业其分摊到每件产品上的固定成本会更小些，故假定f=1，f=2。假定边际成本c=1。此时计算得到10.89%＜θ＜2.412%，即当自身企业对于获取信息所花费的成本占对手企业花费的信息成本的比例在（0.108 9，0.241 2）这个范围内时，企业会选择合作；当自身企业对于获取信息所花费的成本占对手企业花费的信息成本的比例在（0，0.108 9），（0.241 2，1）这个范围内时，企业选择独立经营。

以上结果是基于给定参数值得到的。由函数特征可以推知，当市场规模增大时θ 的值会上升，即若企业要进行合作，企业自身会愿意花费更多的成本去获取信息，因为在市场规模扩大的情况下，获取更多的信息更有利可图；生产产品边际成本的增加会使得θ 值增加，企业会增加对信息成本的投入，这可以理解为在生产产品的边际成本增加时，企业为不让所投入的资金浪费，会尽可能获取有用信息以促进合作的形成，以进一步推动产品销售，故而会增加对信息成本的投入。

三、结论及改进

本文通过对市场上企业类型进行简化并分类，将企业分为领导企业与跟随企业，在成本函数中加入对信息成本的考虑，认为企业的成本与企业自身所投入的信息成本及对手企业所投入的信息成本相关，企业自身所投入的信息成本会增加企业自己的总成本，而企业若能够获取对手企业的信息则能够帮助企业降低自身总成本。运用Stackelberg 模型，在所给的假定条件及参数值下，将企业在单独经营与达成合作之后的成本函数进行比较，发现当自身企业能够获取对方企业的信息在对方企业所投入的信息成本中占比在（0.108 9，0.241 2）水平时，两企业之间倾向于达成合作；否则，企业更愿意独立经营。另外，根据所构建的函数特征可以得到，市场规模与企业信息成本之间存在正向关系，生产产品的边际成本与信息成本之间存在正向关系。