基于逆向强化学习的纵向自动驾驶决策方法*

高振海，闫相同，高 菲

（吉林大学，汽车仿真与控制国家重点实验室，长春 130022）

前言

汽车纵向自动驾驶决策策略研究是现阶段自动驾驶研究领域的核心方向之一。如何学习人的行为规律从而建立决策与控制规则，提高自动驾驶车辆的乘坐体验是当前研究的热点。

在前期的纵向自动驾驶研究中，强化学习方法是主要研究方法之一。强化学习方法是一种用于描述和解决智能体（agent）在与环境的交互过程中通过学习策略达成回报最大化或实现特定目标的方法，与基于规则的系统相比，基于强化学习的系统不需要人为构建规则库，仅通过强化学习算法训练得到决策控制策略控制自动驾驶汽车。Charles 等在协同自适应定速巡航（cooperative adaptive cruise control，CACC）系统中使用强化学习方法，在仿真环境有效地实现CACC 的性能。高振海等在仿真场景中使用Q 学习算法建立纵向自动驾驶决策策略，在多个工况中进行了分析测试。Ye等将深度学习深度确定性策略梯度（deep deterministic policy gradient，DDPG）方法与车辆高保真模型结合起来，换道和跟车行为相结合，将训练模型扩展到更复杂的任务中。朱美欣等基于DDPG 算法考虑安全性、效率和舒适性定义奖励函数，建立了自适应巡航控制算法，其效果优于传统的模型预测控制（model predictive control，MPC）算法。

强化学习方法的奖励函数依然依靠专家的经验设计，拟人化程度不高，得到的策略与人类驾驶员仍然存在差距，使自动驾驶车辆存在乘员舒适性不足、道路上其他驾驶员难以预测自动驾驶车辆的行为等问题。因此，研究者们从不同的角度进行了拟人化自适应巡航控制算法设计。Zhu 等提出了一种模仿人类驾驶员跟车的DDPG 算法，通过比较驾驶员经验曲线和仿真输出的距离、速度定义奖励函数，最终得到了和人类驾驶行为相似的控制效果。Chen 等基于神经Q 学习算法开发了一种个性化自适应巡航制的学习模型，在线学习并模拟人类驾驶员的驾驶策略，具有比传统方法更好的驾驶舒适性。不过，以上研究的奖励函数依然需要人为设计，设计较为主观，需要大量的调试工作才能实现较好的控制效果。

逆向强化学习（inverse reinforcement learning，IRL）是一种能够从专家的演示数据中推断出奖励函数，并利用该奖励函数学习策略，使得在该奖励函数下学习得到的最优策略与专家的策略接近的方法。它与强化学习一样，也是在马尔科夫决策过程的框架内构建的。奖励函数在强化学习任务中起着至关重要的作用。的设置直接确定智能体将采用的策略。逆向强化学习使用逆向思维，假设专家在完成某项任务时，其决策往往是最优的或接近最优的，通过比较专家的交互样本和强化学习交互样本的差别，学习得到奖励函数。因此，逆向强化学习算法能更好地解决自动驾驶任务中奖励函数设计存在的问题，使自动驾驶车辆的行为更接近驾驶员驾驶的车辆。Gao 等使用逆向强化学习方法，对驾驶员的跟车决策行为进行了研究，得到了不同驾驶员各自的奖励函数。You 等使用逆向强化学习算法，通过专家驾驶员示例得到最佳的自动驾驶汽车策略，解决交通环境中自动驾驶汽车的规划问题，以提高通行效率。唐明弘等设计考虑安全性舒适性的奖励函数，通过逆向强化学习方法对奖励函数更新，得到拟人化的ACC决策策略。

本文中提出了一种逆向强化学习汽车纵向自动驾驶决策方法。使用驾驶员在驾驶模拟器上的轨迹数据，基于最大边际逆向强化学习算法并建立相应的奖励函数，得到仿驾驶员的纵向自动驾驶决策策略，最后通过仿真试验对决策策略进行测试，并与驾驶员数据和强化学习策略对比。

1 最大边际逆向强化学习驾驶员决策模型

最大边际逆向强化学习纵向自动驾驶决策模型的框架如图1所示。

图1 逆向强化学习纵向自动驾驶决策算法

首先使用驾驶模拟器采集驾驶员驾驶车辆跟随目标车辆行驶的轨迹数据；

然后对强化学习（Q 学习）方法的奖励函数和值函数进行初始化；

之后训练得到该奖励函数下的控制策略和行驶轨迹，通过计算车辆模型轨迹的特征期望和驾驶员数据的特征期望之间的差距（梯度），更新奖励函数，重新进行强化学习（Q 学习）训练，重复训练，直到梯度足够小，获得仿驾驶员的决策策略。

本文使用最大边际逆向强化学习方法，直接从驾驶员驾驶数据中学习寻找一个能够使强化学习得到的最优策略π控制的动作与驾驶员轨迹中的动作一致的奖励函数。假设奖励函数是特征值(，)与权重矩阵的线性组合：

特征值(，)间接地代表了环境的感知状态。因此，在策略下的动作值函数Q(，)可以表示为

其中：

式中：为折扣因子，本文中值为0.99。μ被称为策略的特征期望，它决定了根据该策略执行的动作的预期折扣奖励总和。

对于不同的两个策略和，如果它们拥有相同的特性期望，它们会拥有相同的动作值函数Q1和Q。

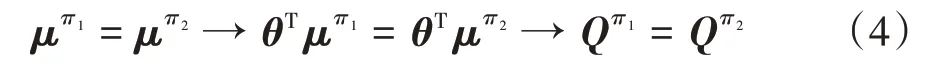
因此，为使逆向强化学习得到的决策策略与驾驶员的决策接近，可以通过最小化驾驶员数据的特征期望μ和学习模型策略的特征期望μ之间的差距方式来实现。

1.1 状态集和动作集设计

在进行自动驾驶的纵向决策任务时，需要考虑本车的行驶状态和本车与目标车的相互运动关系。同时，为了便于设计奖励函数、易于收敛，选择的状态集和动作集所包含的参数不能过多。本文选取的状态集和动作集包含的元素为={，，v}，={a}，如表1所示。

表1 状态集和动作集的设计

状态集大小为（即状态的总数），动作集大小为（即动作的总数）。

1.2 特征值选取和特征期望计算

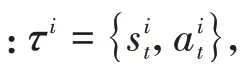
式中s为状态集中第个状态。

然后，我们可以在时刻通过状态-动作特征表示(s，a)来扩展该状态特征。它是大小为×的行向量：

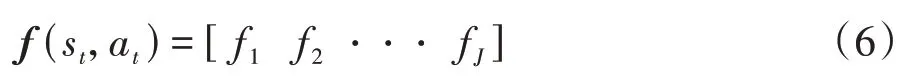
其中f（∈[1，]））为维行向量：

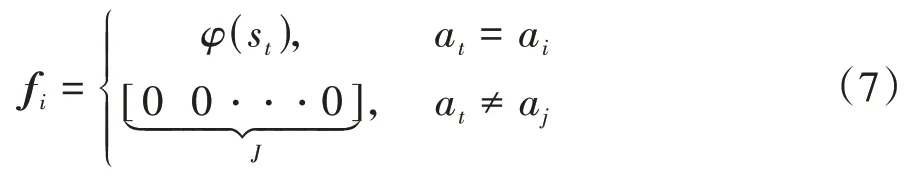
式中a为动作集中第个动作。

驾驶员数据特征期望即为平均每条采集到的驾驶员轨迹数据的特征值之和，如式（8）所示。

同理，学习模型策略的特征期望即为模型输出的轨迹特征值之和，如式（9）所示。

式中M为模型输出的轨迹状态动作对的数量。

1.3 奖励函数更新

在得到驾驶员数据特征期望和学习模型特征期望之后，就可以得到它们之间的差距（即梯度），如式（10）所示。

奖励函数如式（1）所示，奖励函数的更新实际上是更新权重矩阵（权重矩阵的初始值为0-1之间的随机数），本文通过梯度下降法更新权重矩阵：

式中为学习效率，本文中=0.05。

当梯度小于一定值时结束训练，得到权重矩阵和相应的奖励函数，进而可以使用该奖励函数进行强化学习训练获得仿驾驶员决策策略。

2 仿真测试和结果分析

2.1 典型工况驾驶员驾驶数据采集

城市快速路是自动驾驶汽车主要的行驶环境之一，本文使用驾驶模拟器采集熟练驾驶员在3 种常见的城市快速路工况下（如表2 所示）的驾驶数据（本车速度、本车加速度、相对距离、相对速度等）共120组。其中，采集驾驶员驾车以80 km/h（22.22 m/s）的初速度从相对距离40 m 处接近并跟随匀速行驶的目标车数据，目标车车速40 km/h（11.11 m/s）和60 km/h（16.67 m/s）各采集40 组；采集驾驶员跟随目标车40 km/h 匀速行驶，随后加速到60 km/h 匀速行驶，再减速至60 km/h 匀速行驶数据40 组。单组数据时长30-50 s。本实验中驾驶员为男性，27 岁，驾龄7年。

表2 工况设计

将采集到的真实驾驶员实验数据按照不同工况使用Matlab曲线拟合工具箱中的傅里叶曲线拟合法拟合相对距离时间曲线和本车速度时间曲线。如图2和图3所示，图中黑色粗线为拟合的具有统计规律的驾驶员曲线，其他曲线为采集的真实驾驶员实验数据曲线。

图2 接近匀速行驶目标车

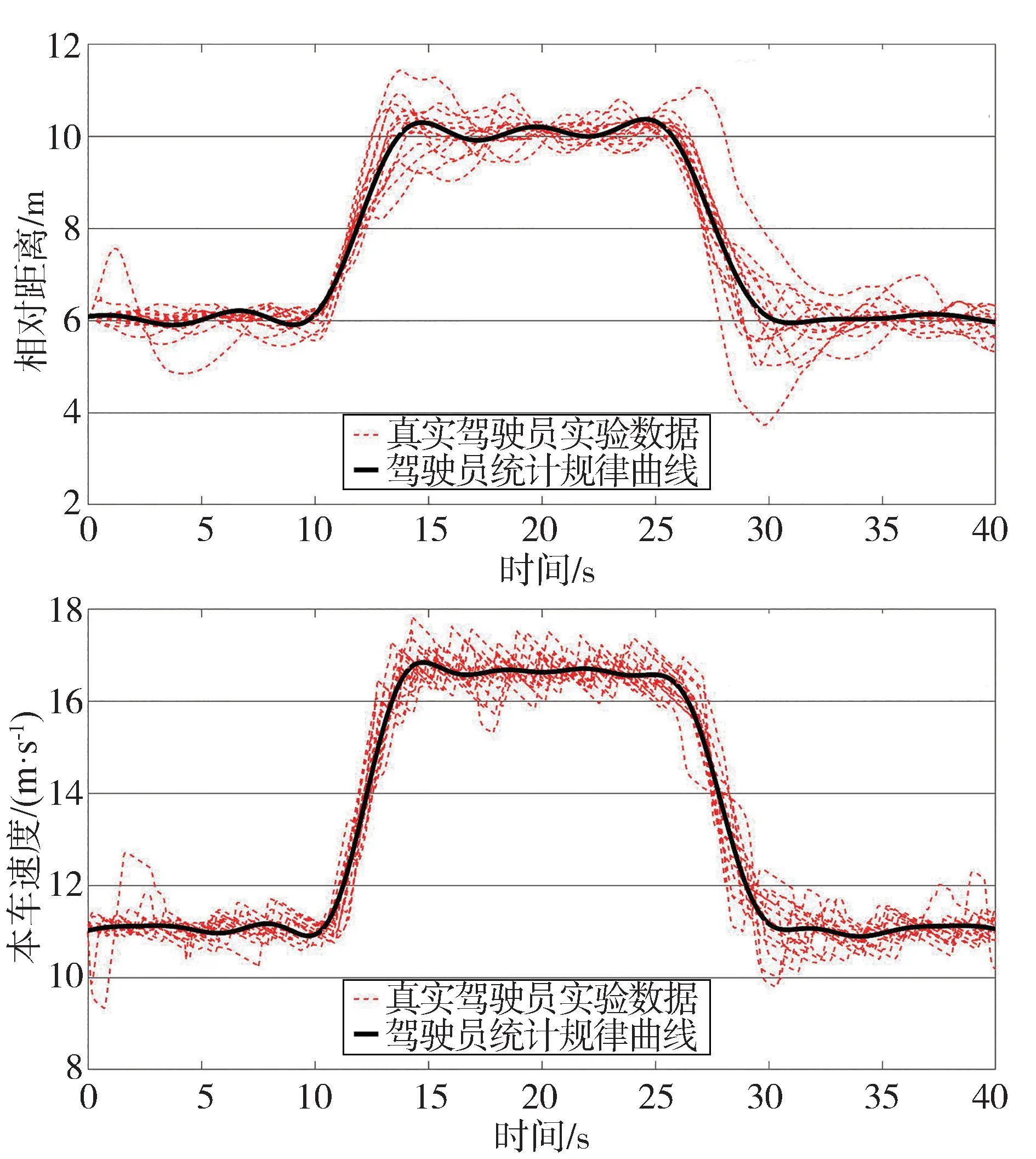
图3 跟随变速目标车

2.2 仿真测试工况与数据分析

为了与逆向强化学习算法的效果形成对比，本文使用前期研究中设计的奖励函数构建了强化学习（Q 学习）算法。使用CarSim&Simulink 联合仿真，搭建车辆动力学模型和仿真训练环境。分别设计3种仿真训练工况（即本车以80 km/h（22.22 m/s）的初速度接近40 km/h（11.11 m/s）匀速行驶的目标车；本车以80 km/h（22.22 m/s）的初速度接近60 km/h（16.67 m/s）匀速行驶的目标车；本车和目标车初速度均为40 km/h，目标车先加速至60 km/h 保持匀速行驶后减速至40 km/h保持匀速行驶）进行强化学习和逆向强化学习训练，并在训练完成后在相应的环境中执行得到的决策策略，测试实验结果。

2.2.1 目标车60 km/h匀速行驶

设置本车初始速度80 km/h（22.22 m/s），目标车以60 km/h（16.67 m/s）匀速行驶，目标车和本车初始相对距离40 m，仿真时长30 s，具有统计规律的驾驶员曲线、强化学习和逆向强化学习仿真结果如图4所示。

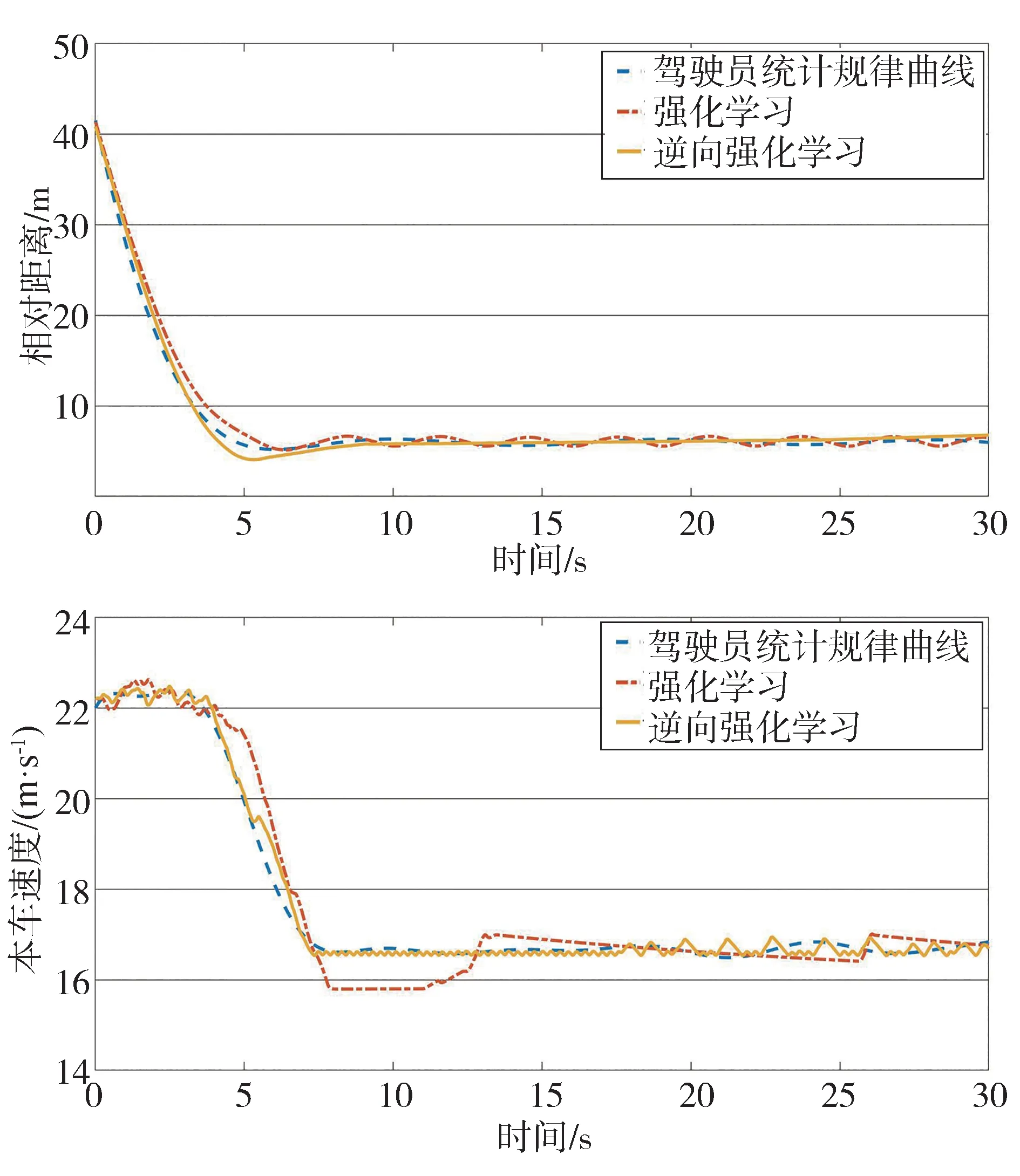
图4 本车接近60 km/h匀速目标车仿真结果

强化学习决策策略与驾驶员曲线的相对距离最大差值为2.79 m，均方根误差为6.96%，本车速度最大差值1.55 m/s，均方根误差2.81%；逆向强化学习决策策略与驾驶员曲线的相对距离最大差值为0.92 m，均方根误差为2.28%，本车速度最大差值为0.76 m/s，均方根误差为0.99%。

2.2.2 目标车40 km/h匀速行驶

设置本车初始速度80 km/h（22.22 m/s），目标车以40 km/h（11.11 m/s）匀速行驶，目标车和本车初始相对距离40 m，仿真时长30 s，具有统计规律的驾驶员曲线、强化学习和逆向强化学习仿真结果如图5所示。

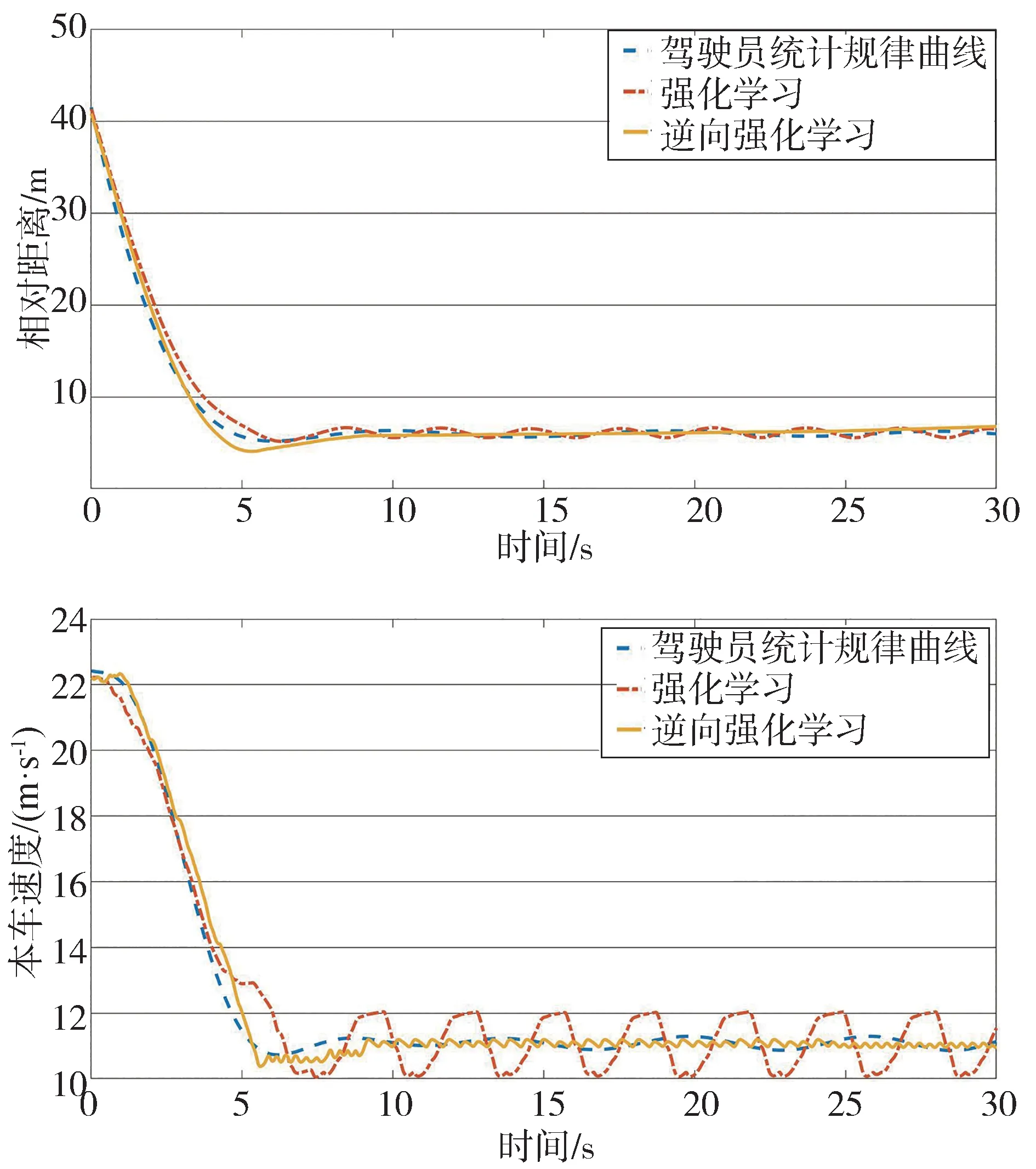
图5 本车接近40 km/h匀速目标车仿真结果

强化学习决策策略与驾驶员曲线的相对距离最大差值为2.74 m，均方根误差为9.75%，本车速度最大差值为1.87 m/s，均方根误差6.71%；逆向强化学习决策策略与驾驶员曲线的相对距离最大差值为1.66 m，均方根误差为6.00%，本车速度最大差值为1.26 m/s，均方根误差为2.80%。

2.2.3 目标车变速行驶

目标车初始速度为40 km/h（11.11 m/s），本车初始速度为40 km/h（11.11 m/s），初始相对距离为6 m，仿真时长40 s。目标车开始时保持40 km/h 匀速行驶，10 s 后目标车开始加速至60 km/h 并保持匀速行驶，25 s 后目标车减速至40 km/h 之后保持匀速行驶。具有统计规律的驾驶员曲线、强化学习和逆向强化学习仿真结果如图6所示。

图6 本车接近变速目标车仿真结果

强化学习决策策略与驾驶员曲线的相对距离最大差值为1.06 m，均方根误差为5.20%，本车速度最大差值为0.83 m/s，均方根误差2.24%；逆向强化学习决策策略与驾驶员曲线的相对距离最大差值为0.95 m，均方根误差为4.96%，本车速度最大差值为1.01 m/s，均方根误差为2.01%。

2.2.4 结果分析

强化学习决策策略、逆向强化学习决策策略的相对距离和本车速度与具有统计规律的驾驶员相对距离和本车速度曲线的最大差距如图7 所示，均方根误差如图8 所示。可以看出，与强化学习决策策略相比，逆向强化学习决策策略与驾驶员的接近程度更高，在完成仿驾驶员决策任务中表现更好。

图7 学习算法与驾驶员曲线的最大差距

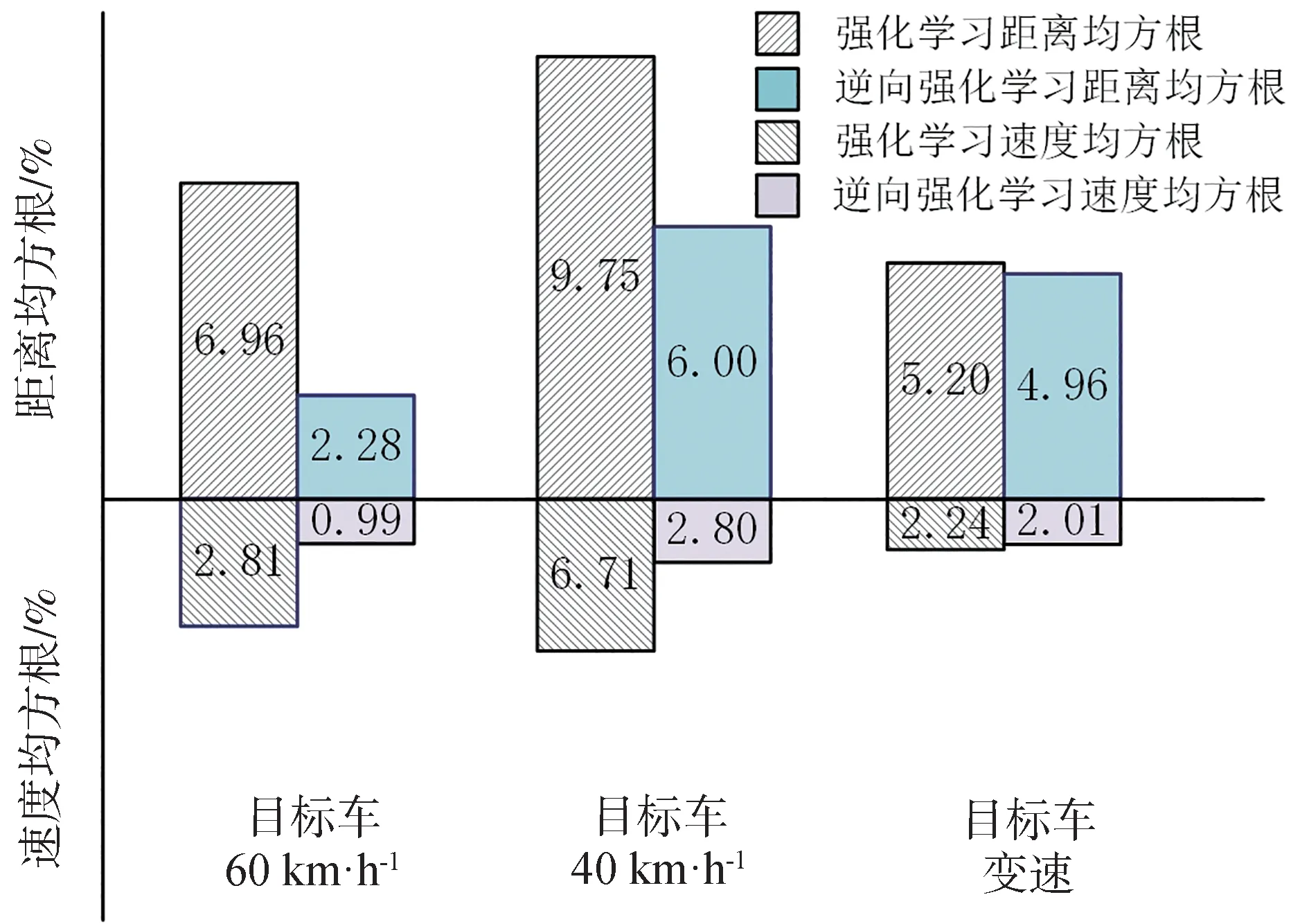
图8 学习算法与驾驶员曲线的均方根误差

3 结论

本文中提出了一种基于逆向强化学习的仿驾驶员纵向自动驾驶决策算法，并在仿真环境下进行了测试验证。

（1）建立了反应车辆状态-动作特征的特征矩阵并明确车辆状态-动作信息和特征值之间的映射关系，利用驾驶员轨迹数据的特征期望和执行模型输出的策略得到的轨迹的特征期望，通过梯度下降法学习得到奖励函数。

（2）从实验结果来看，与强化学习算法相比，逆向强化学习算法训练后得到的决策策略在各个工况下与人类驾驶员数据的均方根误差减小了0.23%～4.68%，差距更小，一致性更高。

（3）本文中将逆向强化学习算法应用于纵向自动驾驶决策任务中，直接输出期望加速度进而实现车辆纵向控制，实验结果表明逆向强化学习算法能够实现仿驾驶员纵向自动驾驶决策。在后续的研究中，针对现有的逆向强化学习算法存在的当状态空间包含的状态过多时算法不易收敛、速度和距离出现波动等问题，以神经网络代替连续状态空间的值函数，探索仿驾驶员深度逆向强化学习自动驾驶决策算法。