燃料电池气体扩散层纤维孔隙特性对液态水传输的影响分析*
刘青山,兰凤崇,陈吉清,王俊峰,曾常菁
(1. 华南理工大学机械与汽车工程学院,广州 510640;2. 华南理工大学,广东省汽车工程重点实验室,广州 510640)
前言
质子交换膜燃料电池(proton exchange membrane fuel cell,PEMFC)具有工作温度低、污染低、能量转换率高等优点,是作为车载动力的理想来源。车用PEMFC 动力系统的高功率输出特性导致电池的气体扩散层(gas diffusion layer,GDL)内部会有大量的液态水存在,见图1(a),而系统的连续变载工作特点又要求GDL 有较高的传质能力。GDL 的制造方法导致其纤维摆放具有随机性,见图1(b),这导致其纤维孔隙特性,包括孔隙率、孔隙分布导致的各向异性传质能力和孔径大小与分布不均等在一定范围内随机分布,无法对这些属性进行精确控制。由于GDL 的厚度有明确限制,各属性之间的相互影响增强,所以GDL 纤维孔隙特性对其传质能力的影响是综合且复杂的。在这种情况下,对GDL 传质能力的控制和优化比较困难。基于此而开发的新一代有序化GDL、金属GDL 能够准确控制内部的孔径大小和分布,从而准确控制其传质能力。理清、研究GDL 内部的液态水传递行为有助于找出影响液态水运动的关键因素,对其传质能力的设计和FC 水管理能力的增强有重要意义。

图1 PEMFC的结构组成和液态水从CL进入GDL的示意图
在GDL 和气体流道(gas flow channel,GC)的整体系统内描述液态水的运动方面,Niu 等使用流体体积(volume of fluid,VOF)方法研究了2 个相邻GC之间GDL 中的液态水-空气横向流动。Niblett 等使用VOF 方法进行了动态两相流模拟,研究了GDL孔隙形态、微孔层(microporous layer,MPL)缺陷和GDL 与GC 之间的相互作用对系统中水动力学的影响。
在GDL 内部的液态水运动描述方面,Jiao 等采用VOF 方法求解蒸汽/凝结水两相流问题,比较了在不同电流密度和环境温度下,GDL 中有/无肋的蒸汽凝结过程。Jiao 等研究了振动条件下GDL 中水分的输运,水入侵倾向于从GDL 的两侧开始,然后扩散到中心区域,与无振动情况相比,垂向和水平振动情况下的水饱和度均较高。
在GDL 内部湿润性对液态水运动的影响方面,Niu 等使 用VOF 方 法 研 究 了 不 同 聚 四 氟 乙 烯(polytetrafluoroethylene,PTFE)负荷量对混合润湿性GDL 中毛细压力()与含水饱和度()关系(-)的影响。Niu 等研究了PTFE 在干燥的碳纸上的加载效果和不同局部水剖面与孔隙度分布对穿过平面和平面内方向有效氧扩散率的影响。
在GDL 压缩对内部液态水运动的影响方面,Zhou等采用有限元方法对重建的GDL微结构进行了固体力学模拟,观察到压缩GDL 的各种孔隙形态和分布。采用VOF 模型模拟了GDL 的两相流。Zhou 等采用FEM 进行夹紧压力模拟,考虑了GDL变形,采用VOF 对不同表面润湿性分布方案的压缩GDL微结构中的两相流进行了模拟。
GDL 作为PEMFC 内部传热传质的关键部件,其结构特性对水传递性能有重要影响。目前的研究趋势表明,其材料金属化、孔隙结构有序化均有利于对内部的孔隙控制。研究针对有序化GDL 内部液态水传递的关键影响参数,GDL 纤维的形状对液态水运动状态的影响机理等,对有序化GDL 的设计和优化具有参考意义。本文中建立了能捕捉液态水在纤维间运动的两相VOF 模型来研究影响GDL 内液态水传递的关键因素,分析了不同孔隙率、纤维形状和接触角下GDL 内部液态水的运动过程。最后,给出了影响GDL内部水传递的关键参数。
1 纤维间液滴运动状态的捕捉
为捕捉GDL 内微孔间的液态水运动状态,基于燃料电池内部实际状态做了如下假设:由于FC内部的气体和液体流速均较低,雷诺数较小,可以假设其两相流是不可压缩的层流;FC 在稳态运行时,各项操作参数基本保持恒定,可以假设空气和水的物理性质是恒定的;研究过程的持续时间在ms 量级,纤维表面的疏水剂损耗很小,可以认为纤维表面的接触角保持恒定;由于FC 的工作温度为50-80 ℃,此时液态水的蒸发速率较低,且研究持续时间很短(ms 量级),可以认为流体的传递性质保持不变,过程中不发生相变。
1.1 计算方法
将VOF 模型的控制方程和描述液态水穿过纤维运动形态的方程通过用户自定义标量、内存、用户设定函数(user defined function,UDF)和修改源代码等方法整合至ANSYS Fluent软件进行模拟。为提高求解的稳定性,指定气体为主相,液体为次相。VOF模型具体见文献[2]~文献[9],这里着重于描述液态水穿过纤维运动形态的方程。
对于GDL 内部的多孔结构,表面张力与平面不同。两个圆形纤维之间的液体连接如图2 所示。半填充角为

弯月面主半径和半轴长分别为

式中诸参数见图2,其中为润湿角,也称接触角。

图2 圆形纤维间液滴运动的数学关系
和可以根据不同润湿性(接触角)壁面的情况简化为
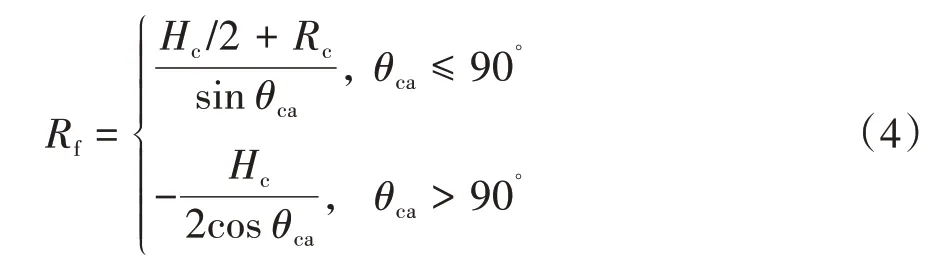

毛细力由两个力分量组成。一个是表面张力,与固体表面连接点处的外圆相切并作用在润湿圆周处,其方向的分量为
式中为与表面张力有关的参数。
另一个力来自于毛细压力,可以通过Laplace-Young 方程描述,对每根纤维的轴向投影润湿面积计算得到:

1.2 边界条件
用于本次仿真的物理性质是在温度为60 ℃下获取的,如表1 所示。从液态水入口以0.1 m/s 的速度注水,以模拟PEMFC 运行过程中的液态水渗透情况,这个速度在其他VOF 研究PEMFC-GDL的范围内(0.011~1 m/s)。与实际运行的PEMFC 内的水渗透速率相比,提高注水速率可以减少计算时间。仿真用到的属性列于表1 中,其他属性示于图3 中,进气速度和结构参数采用文献[3]中的取值。

图3 计算域及边界条件

表1 物理性质与结构参数
1.3 计算域
用于仿真的计算域和边界条件如图3 所示,代表纤维直径为20 μm的碳纸。因为真实MPL中的孔隙非常紧密,水一般通过其裂痕传递,这里假设裂痕处于GDL 中间位置。文献[3]中进行了网格敏感性分析研究,发现使用单元尺寸在1~2 μm 之间的网格足以保持质量守恒和界面形状精度,界面形状的差异小于1%。因此,本文中采用的网格尺寸为2 μm进行仿真,以确保网格的独立性。文献[3]中的研究表明,就平面内方向的扩展而言,3D 和2D 模拟之间的界面形状和拓扑之间具有较高的相似性。因此,采用2D 模拟有效且能降低计算成本。由于时间步长是影响瞬态求解结果的重要因素,采用UDF 对求解过程中的时间步长进行自适应调整,以保证在仿真过程中的全局Courant数始终<0.1,同时又能保持较高的求解效率。
1.4 模型有效性验证
采用Afra等的工作对液态水的运动状态进行验证,实验结果如图4(a)所示,图4(b)是本次模拟的结果,两者采用的计算域和各种条件相同。由于仿真中采用了自适应时间步长,故结果中的流体体积与实验的体积不相等,但是接近。在各自流体体积对应的状态图中,模拟结果能够捕捉流体在GDL内的各种实际运动状态。流体在GDL 底部的横向扩散(图4(a).2),在GDL 纤维间的爬升(图4(a).3)和在GDL 中部纤维间的横向扩散(图4(a). 4)等都能有效捕捉(见图中的圆圈标记)。经验证,本研究所开发的模型适用于研究从GDL 内部到GC 的完整液态水运动。

图4 非湿润流体在GDL内运动的实验与仿真结果对比
2 液态水运动影响因素分析
为找出影响GDL 内液态水运动状态的关键属性,提升FC 的水管理能力,考虑了GDL 的孔隙率、纤维形状和纤维接触角等因素。
2.1 孔隙率对GDL内水分布的影响
对圆形GDL 纤维形状的3 种孔隙率情况进行了研究,分别为0.6,0.7,0.8。= 0.6 时,FC 内液态水的运动状态如图5 所示(仅绘制一个周期,之后的轮廓图类似)。在=0-0.8 ms之间,液态水从MPL裂痕处进入GDL,沿着GDL 纤维间的通道爬升,在=0.8 ms 时到达GDL|GC 的交界面。在=0.9-1.9 ms 之间,液滴在GDL 表面的中心逐渐成长。在=2.0-4.8 ms之间,由于液滴的不断增大,其迎风面积的增加导致空气流动带来的拖曳力大于其表面附着力,因此液滴朝着出口方向蠕动前进。在=4.9-5.0 ms 之间,液滴接触亲水性的GC 底部壁面=90°,其形态迅速由液滴转换成液膜,加速了液态水的排出。在=5.1-6.0 ms之间,液态水到达出口,形成了稳定的排水流。在=6.1 ms 及之后,由于液态水的持续排出,水量的减少导致液滴向出口方向收缩,液滴的运动进入下一个循环,即收缩成液滴、生长、蠕动前进、排出。由于从图片即可清晰地分辨液态水的运动过程,后续液态水的运动状态不再赘述。
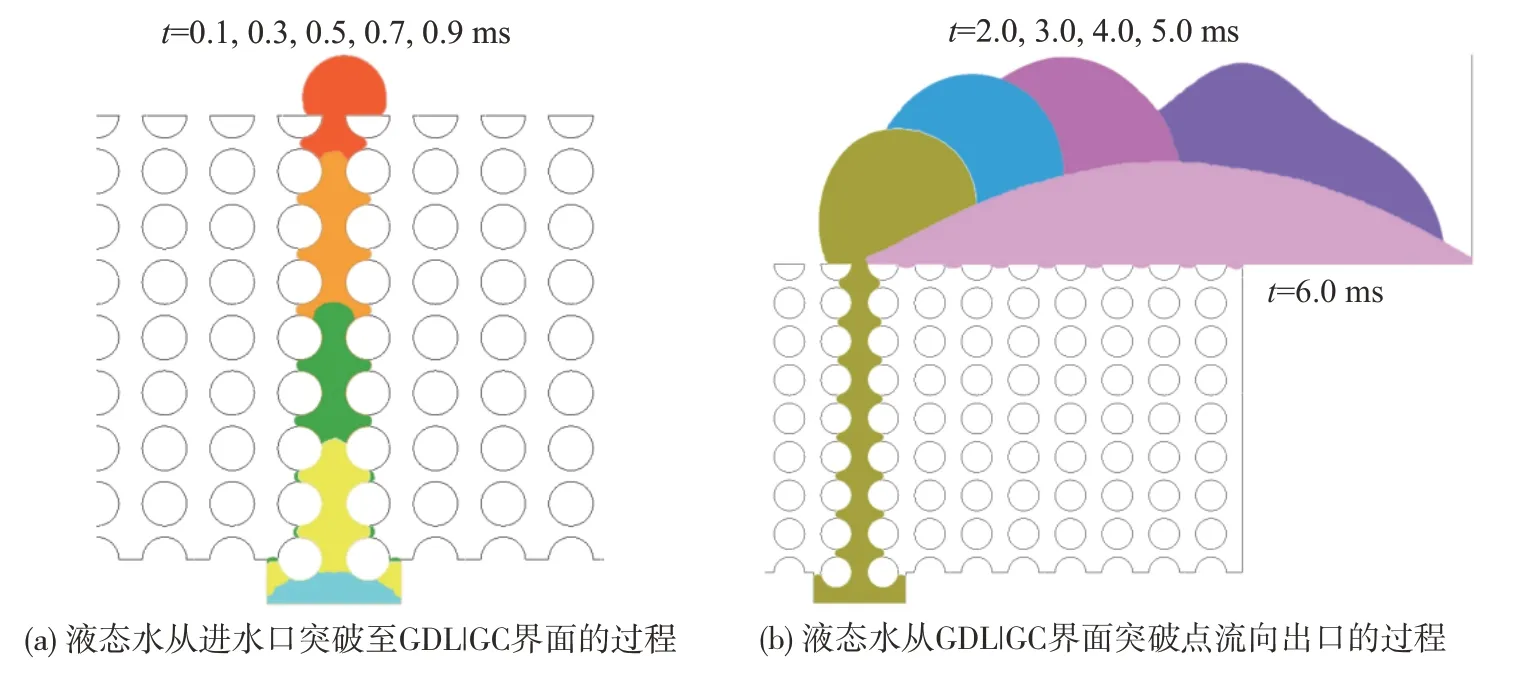
图5 ε = 0.6圆形纤维的电池内液态水运动状态图

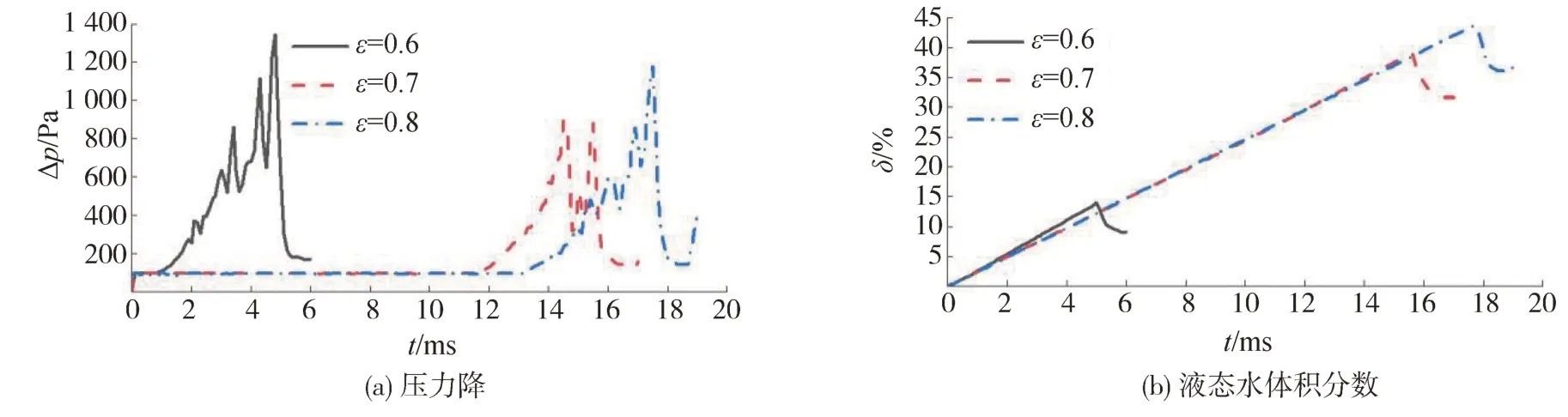
图6 不同ε下圆形纤维的压力降和液态水体积分数随时间变化图
2.2 GDL的纤维形状对其内部水分布的影响
为分析GDL 的纤维形状对液态水运动的影响,选取了3 种形状(圆形、正六边形和正方形)进行研究。由上一节的结论可知,= 0.6时FC排水能力最强。因此,以= 0.6 的情况进行研究,保持纤维的横截面积不变(以圆形纤维的横截面积为基准),使纤维均匀分布于GDL 尺寸范围内,同时使内部所有纤维的横向、纵向间距分别相等。纤维形状为正六边形、正方形情况下,FC 内的液态水运动状态分别如图7和图8所示。

图7 ε = 0.6正六边形纤维的电池内液态水运动状态图
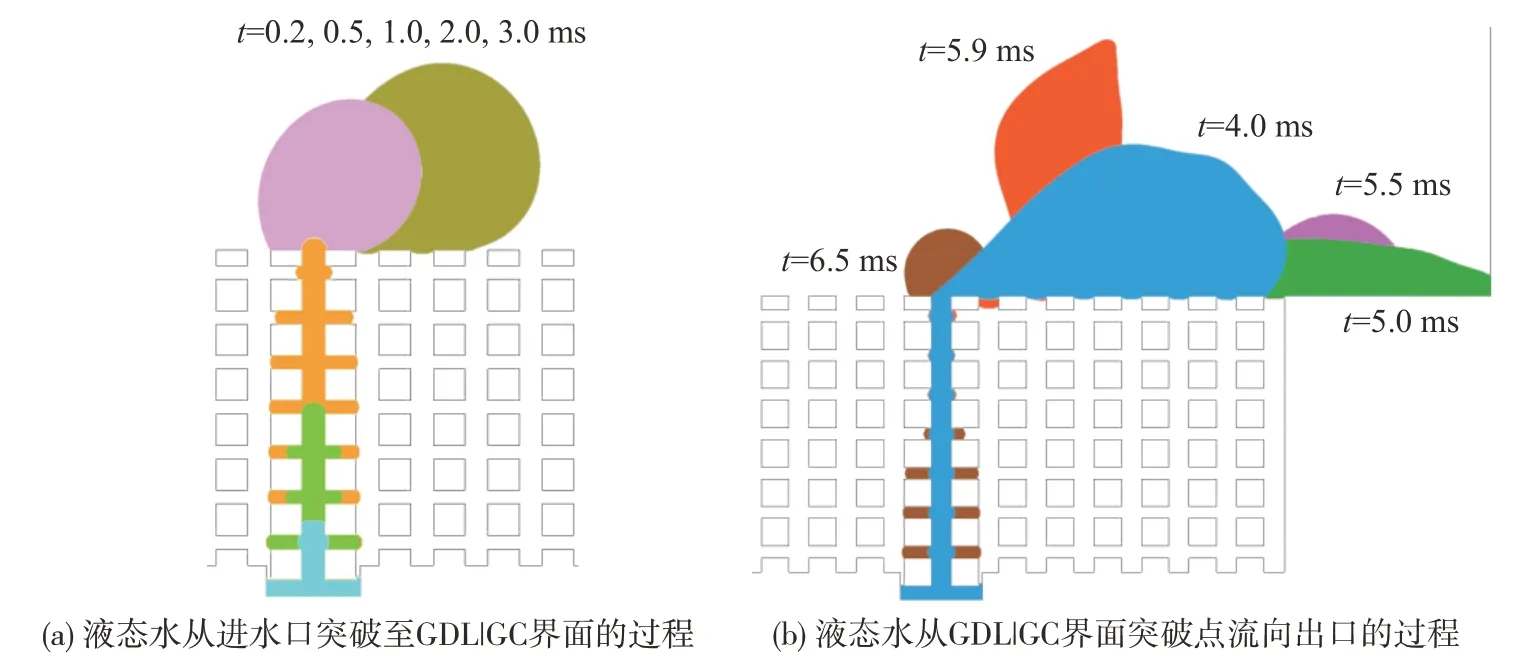
图8 ε = 0.6正方形纤维的电池内液态水运动状态图

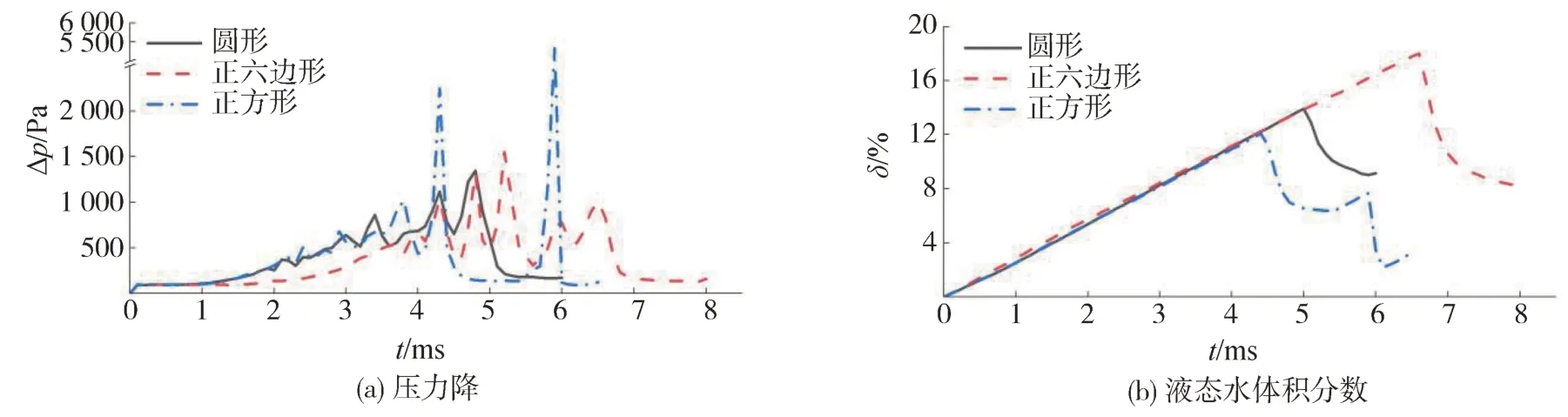
图9 在ε = 0.6时,不同GDL纤维形状下的压力降和液态水体积分数随时间变化图
2.3 GDL纤维间距纵横比对内部水分布的影响


图10 在不同ε下正六边形纤维的压力降和液态水体积分数随时间变化图


图11 在不同ε下正方形纤维的压力降和液态水体积分数随时间变化图
为此,对以上仿真使用的模型信息和结果进行了汇总,如表2所示。由于GDL 纤维的形状不同,在GDL 孔隙率变化时,纤维的排列状态和纤维之间的间距也会发生变化。纤维的横向间距和纵向间距的相对比值会影响液态水的突破方向。从表中可以看出:在GDL 内发生横向扩散的几个案例中,纤维间距的纵横比均高于125%;在未发生横向扩散的案例中,均低于74%。因此可以认为,GDL 的是决定内部液态水是否横向扩散的关键因素,且GDL 的临界在74%~125%之间。对在80%~120%情况进行了仿真,发现在为100%时,液态水在GDL 内部同时发生横向和纵向扩散。小于95%时只发生纵向扩散,大于105%时只发生横向扩散。因此,可以认为GDL 的临界为100%。为了使GDL 内的液态水尽快排出,应该使小于100%,以避免发生横向扩散。

表2 不同GDL孔隙率和纤维形状下的结构与液态水变化信息汇总

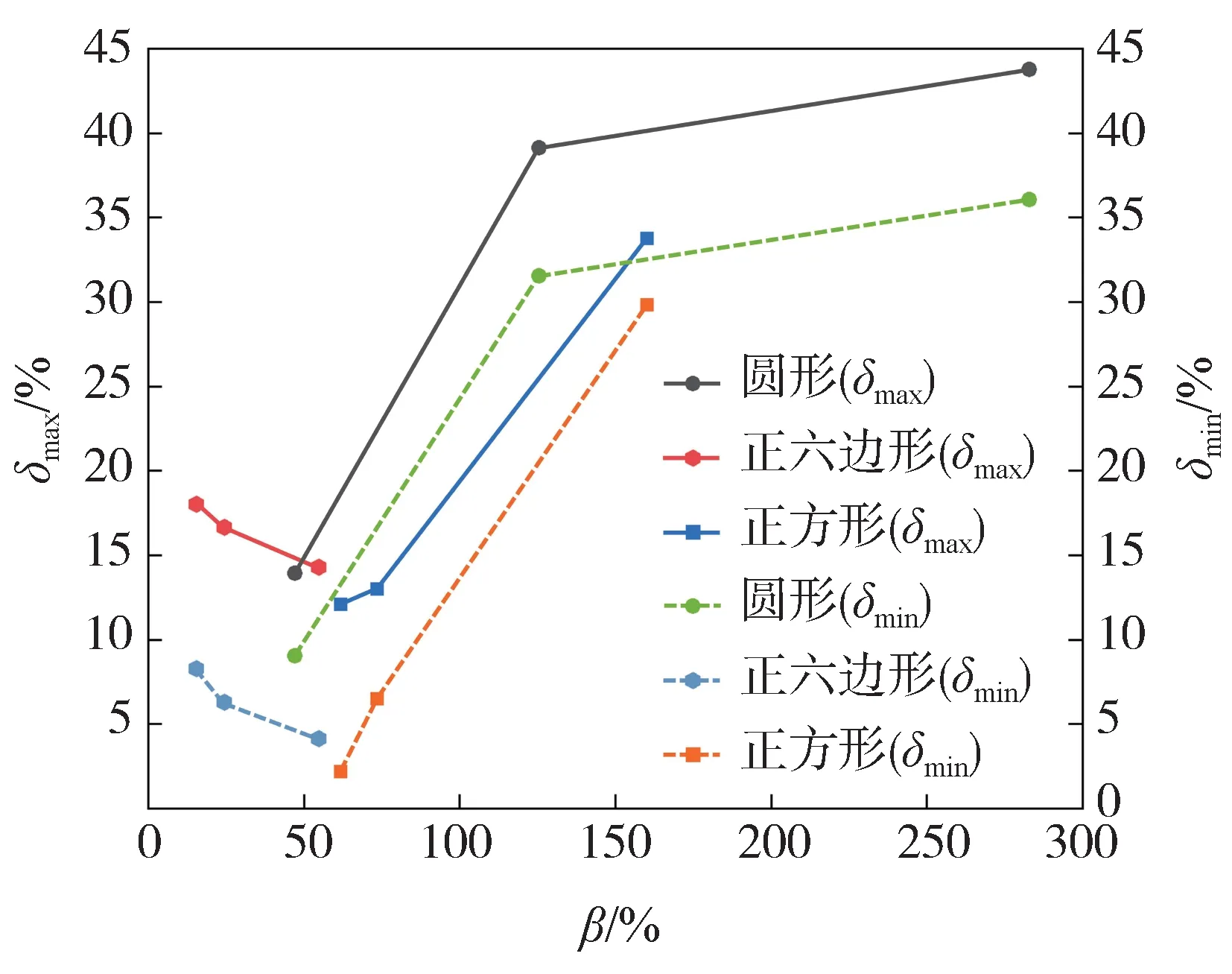
图12 β与各GDL纤维形状情况下的关系


图13 相同β下,不同纤维形状的液态水体积分数变化图
2.4 纤维表面接触角对GDL内水分布的影响
GDL纤维表面的润湿角会影响附着在其表面的液态水状态,因此对液态水的运动产生明显影响。接下来研究= 0.8时3种(= 110°,120°,130°)下液态水的运动状态。= 110°情况下的正方形纤维液态水运动状态如图14所示。
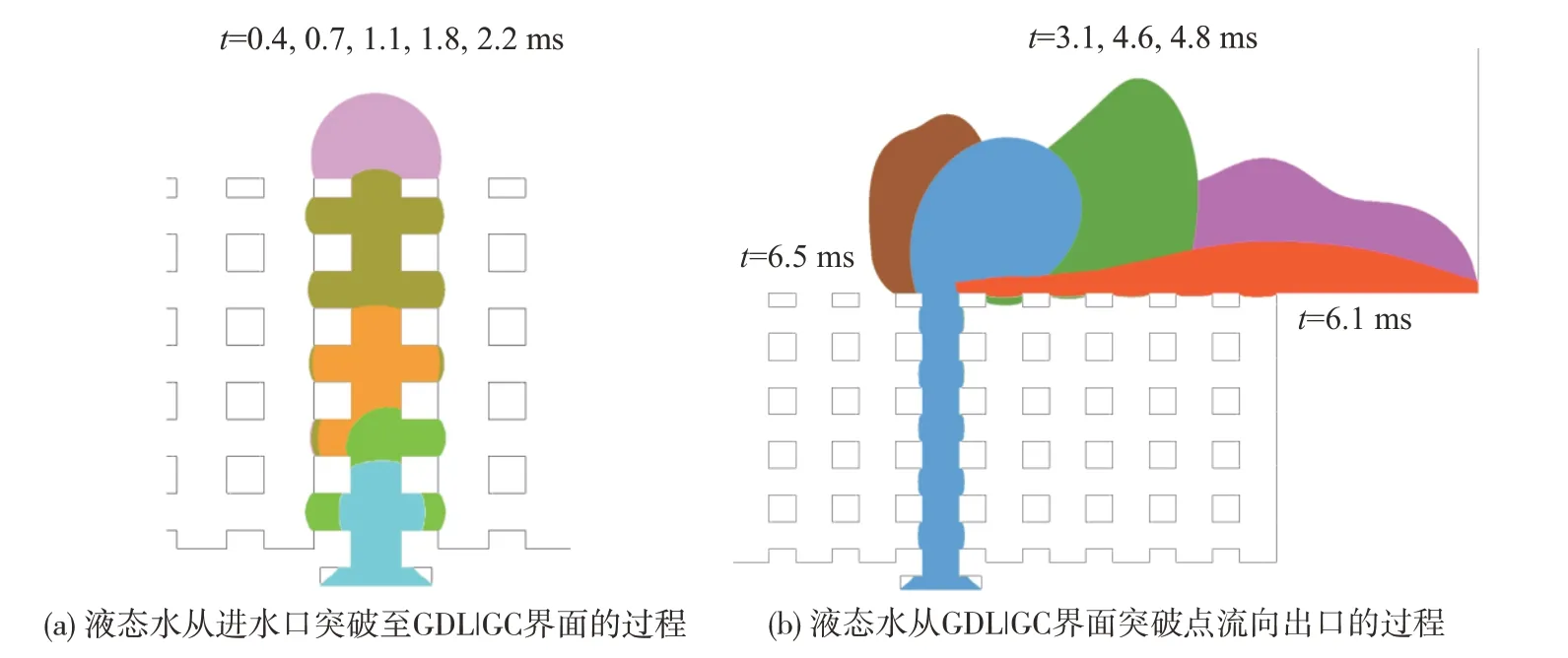
图14 在ε = 0.8,θca = 110°下的电池内液态水运动状态图


图15 在ε = 0.8时,不同θca下正方形纤维的压力降和液态水体积分数随时间变化图
2.5 接触角分布对GDL内水分布的影响
接下来研究空间分布对内部液态水传递的影响,分布可以分为沿GC(横向)和垂直GC(纵向)两个方向。将GDL 内纤维分成5 个部分,从130°持续变化到110°,间隔为5°,横向变化的示意图如图16所示。
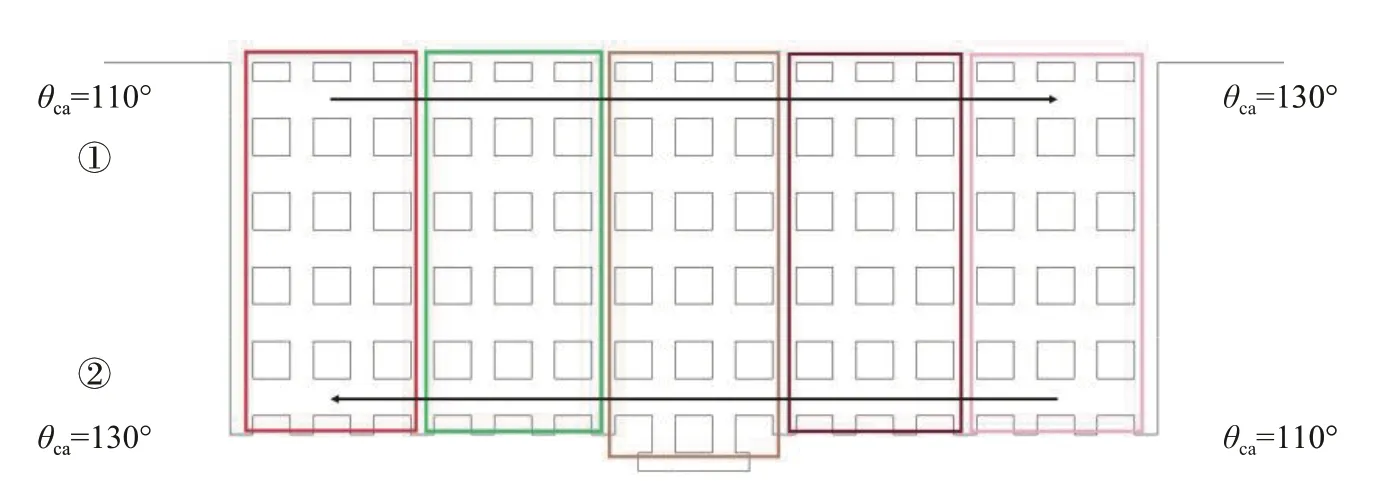
图16 GDL正方形纤维表面接触角横向变化示意图
接着对正方形纤维= 0.7 时,沿着GC 方向增大和减小两种情况下的液态水运动状态进行仿真。= 110° →130°横向变化情况下的FC 内液态水运动状态如图17所示。
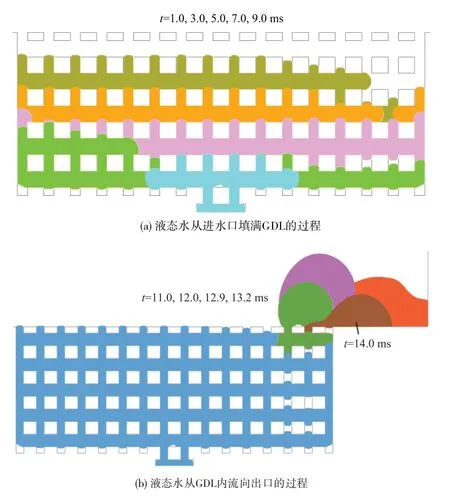
图17 正方形纤维ε = 0.7,θca = 110° →130°横向变化情况下的电池内液态水运动状态图

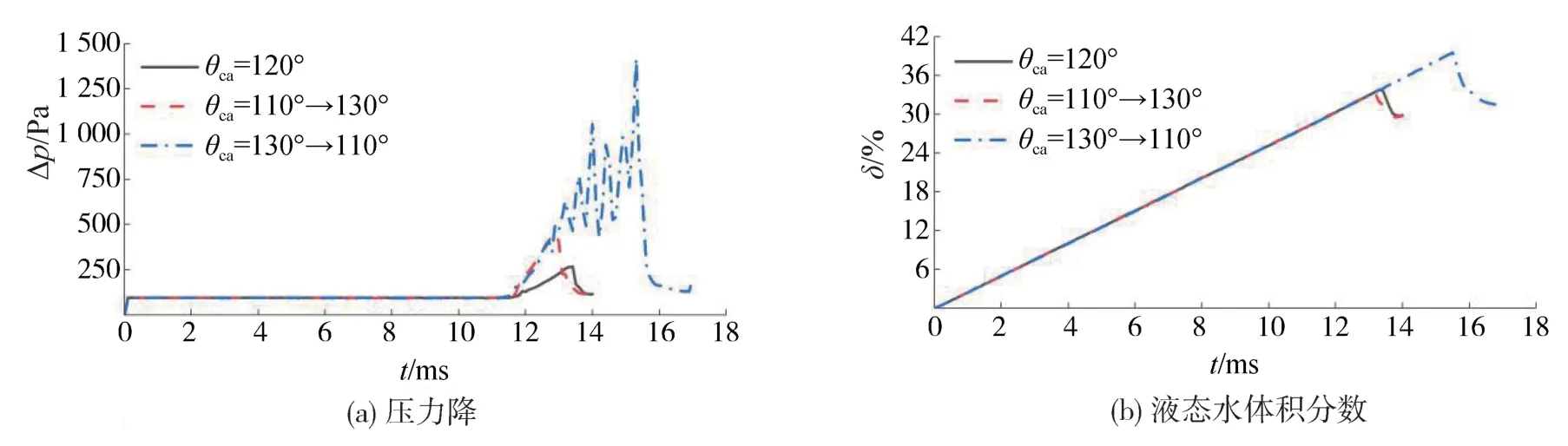
图18 正方形纤维ε = 0.7时,θca横向变化情况下的压力降和液态水体积分数随时间变化图
纵向变化的示意图如图19 所示,在这里,研究了= 0.8时沿着垂直GC方向减小和增大两种情况下的液态水运动状态。= 130° →110°纵向变化下的FC内液态水运动状态如图20所示。
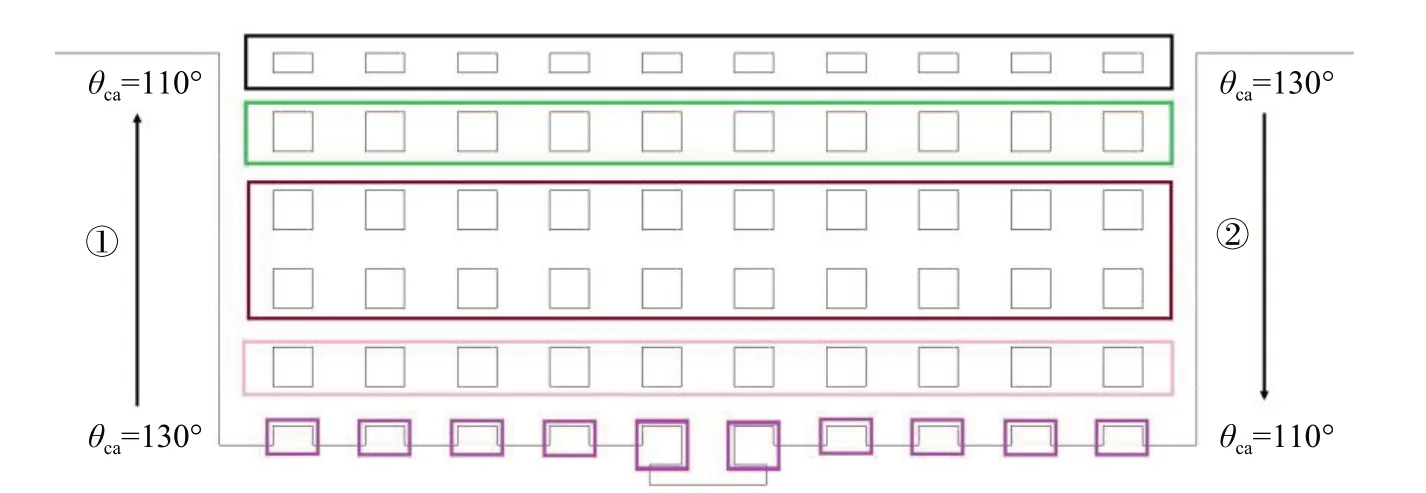
图19 GDL纤维表面接触角纵向变化示意图

图20 正方形纤维ε = 0.8时,θca = 130° →110°纵向变化情况下的电池内液态水运动状态图


图21 正方形纤维ε = 0.8时,θca纵向变化情况下的压力降和液态水体积分数随时间变化图
3 结论
(1)开发了一个两相的VOF 模型,分析了多孔结构与平面之间的表面张力差异,考虑了纤维孔隙间距、形状和结构尺寸对液态水运动的影响,能够有效地捕捉到GDL内部的液态水运动状态;
(2)GDL 的纤维间距纵横比决定了液态水是否在GDL 内横向扩散,对GDL 的排水能力有重大影响,纵横比应小于100%,这在随机结构GDL 内很难准确控制,有序化GDL应准确控制;
(3)随机结构GDL 孔隙率的变化会改变孔隙的大小和孔径分布,导致纤维间距纵横比的改变,从而影响内部液态水的运动状态,有序化结构GDL 可以在不同孔隙率保持相同的孔隙特性;
(4)GDL 的纤维形状会影响液态水穿过纤维间隙的运动状态,在相同纵横比情况下,以圆形为基准,液态水体积分数为标准,正六边形的排水能力约强10%,正方形约低10%;
(5)增大接触角能增强GDL 的排水能力,接触角横向分布对GDL 排水能力的影响不明显,接触角从GDL 的CL 侧向GC 侧逐渐增大的纵向分布能显著提升GDL 的排水能力,需要根据目标排水能力合理选取接触角及其分布。

