电磁场作用下金属凝固过程的建模方法

殷子豪 张 帆 仲红刚

（上海大学先进凝固技术中心，上海 200444）

金属的凝固是非常复杂的高温动态过程，金属在自然状态下的凝固组织往往由于温度梯度而存在凝固的先后次序，从而实现了固/液界面的推进。这一行为最终导致金属件心部产生缩松缩孔以及成分不均匀等各种缺陷。

由于高效、非接触的特点，施加电磁场改善金属凝固组织已成为凝固领域研究的重点。早在1922年，Mcneil就提出了电磁搅拌的专利；20世纪50年代初，Junghaus和Schaaber等在德国Hückingen连铸机上首次试验了电磁搅拌[1]，以改善铸坯质量。美国麻省理工学院Flemings等最早采用脉冲电流细化金属凝固组织[2]，之后大量学者展开了脉冲电流[3-6]与脉冲磁场[7-13]对金属凝固组织影响的一系列研究。上海大学翟启杰团队将脉冲磁致振荡凝固均质化技术成功运用于工业实践[14-17]。

电磁场的引入使凝固过程更加复杂，需要对熔体流动及组织演变行为进行更深入的研究。但由于受实际环境的限制，一般很难直接通过试验得到结果。近几年计算机模拟技术的飞速发展，使得数值模拟成为研究这一过程的重要手段之一。但数值模拟很难将所有的变量都考虑到模型中，因此合理的假设是建立数学模型的必要步骤。根据模型所求解的物理量，忽略一部分影响相对较小的变量，或者将其等效在其他物理量上，以便于方程的求解。通常，凝固过程数值模拟需要在建立几何模型后对不同的几何域定义不同的物理意义，并根据网格划分进行离散化处理，最终归结为多元代数方程组，求解后获得数值解。通过调整网格划分与求解方式的设置等可以提高数值解的可靠性，进一步通过实验室或者工业生产的数据进行校正拟合与验证，才能得到相对可靠的数值模型，进而从后续的参数化研究中得到接近真实的定量分析结论，以深刻理解金属熔体凝固过程。

本文综述了电磁场作用下金属凝固过程的数值模拟方法及应用，阐述了电磁场作用下流场与温度场的耦合模型，分析比较了不同模型的应用环境，并展望了未来的发展方向。

1 熔体内电磁场数值模拟

1.1 矢量势法

Fujisaki等[23]将电磁场视为准稳态场，通过A-φ变量有限元法计算电磁场，对比了旋转搅拌和平行搅拌的电磁效应，发现旋转磁场下的电磁力存在涡流分布特征，这有利于提高铸坯的表面质量及优化夹杂物。Kolesnichenko等[24]通过边界元法计算了圆形立式连铸机二冷区的二维电磁场分布，通过边界元法求解空气中的磁场分布，获得的表达式作为求解金属熔体内部电磁场的边界条件，再利用A-φ法的有限差分方程求解熔体内部电磁场分布。

Zhang等[10]基于ANSYS中的磁场模块通过磁矢量势法得到空间电磁场分布。在模拟引入谐波磁场时，将体积力分为时间相关分量和时间无关分量。通过时均体积力，解决电磁场周期与熔体动量响应时间尺度相差较大的问题。对电磁场和流场采用不同大小的网格，利用线性插值法将电磁力精确插入不同的网格中：

式中：FFLUENT为插值点的时均电磁力密度，该点为FLUENT单元格的质点；FiANSYS为ANSYS中第i个点的时均电磁力密度；di为插值点和第i个点的距离，如图1所示。

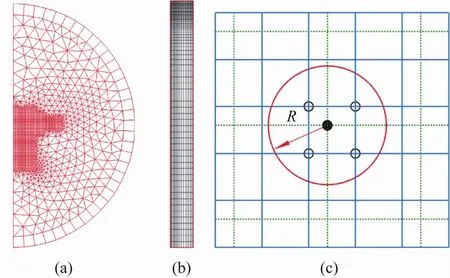
图1 ANSYS（a）和FLUENT 网格（b）及插值流程示意图（——ANSYS；···FLUENT）（c）Fig.1 Mesh in ANSYS（a）and FLUENT（b）and schematic diagram of interpolation procedure（——ANSYS；···FLUENT）（c）

1.2 直接求解法

通过直接法[25]也可求解空间磁场分布，即对磁场强度H直接求解，根据Biot-Savart定律，有：

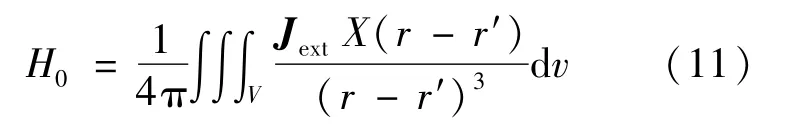
式中：V为材料体积的积分；r为离源点的距离；r′为积分用虚拟变量。

Meyer等[25]利用直接求解法对连铸方坯和板坯的电磁搅拌过程进行数值模拟，发现三维模型的模拟结果与二维模型的不同，即线圈上下边缘处铸坯横截面上电磁力明显衰减，纵截面上电磁力以轴向分量为主。

Räbiger等[26]通过OPERA 3D 程序模拟了脉冲电极从顶部导入GaInSn共晶合金中的电磁场与流场分布规律。针对电荷守恒和不同电导率材料界面处的电流密度J连续性，即Jn＝－σ1n×▽φ1＝ －σ2n×▽φ2，求解电势的Laplace方程▽2φ＝0。其中感应磁场利用Biot-Savart定律通过电流密度J＝σ（－▽φ）计算，即：

电势的边界条件通过电极末端的电流幅值定义：IDC＝∫Ads×J，其中A为电极横截面积。模拟发现感应磁场主要集中在电极附近，且最大值出现在电极表面。感应焦耳热主要分布在电极底部，电极底部的电流密度远大于其他区域。电磁力同样集中于电极底部，方向主要向下。Xu等[27]将电极从侧面导入工业纯铝中，脉冲电流的表达式可表示为i（t）＝ I0e－αtsin（2πft），其中I0为电流幅值，α为衰减系数，f为电流频率。为了研究电极位置对组织的影响，分别模拟了电极两端位于一侧和两侧的情况。

Zhang等[28]模拟了脉冲电流作用下定向凝固的铝硅合金熔体流动情况，熔体中洛伦兹力分布如图2所示。硅颗粒非对称时，洛伦兹力的变化主要出现在糊状区，且初生硅附近的糊状区受到的洛伦兹力减少，其余区域均增大；V型界面上方，洛伦兹力明显增强，洛伦兹力的总和将熔体从熔池边缘推向中心。

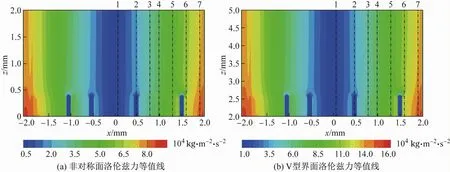
图2 脉冲电流作用下熔体中洛伦兹力分布Fig.2 Distributions of Lorentz force in melt under electric current pulse

式中：Ik和Φk分别为第k匝线圈多相电流的幅值与相移；dlk为线圈的单元长度；dV为熔体的单元体积；｜r－r′｜为熔体中某一点到各自积分单元的距离。

式（16）等号右边第一项表示磁场的旋转部分，第二和第三项则分别表示线圈与感应电流对磁场的影响，因此可以涵盖任意形式感应线圈的电磁场计算，并且不涉及自由空间的电磁场计算，大大节省了计算机的运算时间与存储空间。这是首次尝试在三维坐标系下进行方坯和板坯内的电磁场与流场耦合计算，也为今后对方坯和板坯内电磁场、流场和温度场的复杂建模提供了理论框架。

2 电磁场作用下流场与温度场耦合模型

由于电磁场、流场与温度场的时间尺度问题，往往先对电磁场单独求解，再对流场和温度场进行耦合求解。目前常用的流场数值法为雷诺平均纳维-斯托克斯模型（Reynolds-averaged Navier-Stokes equations，RANS）[30]，由于RANS 采用了经验壁面定律，可在粗大边界层上捕捉大速度梯度，因此这种方法具有很高的计算效率，且可精确估计稳态流型[31]。

描述熔体流动的基本方程如下：

不可压缩流体的质量守恒方程：

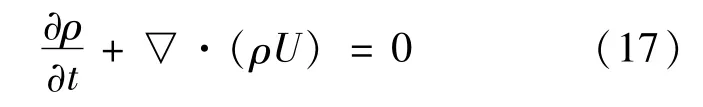
不可压缩流体的动量守恒方程：

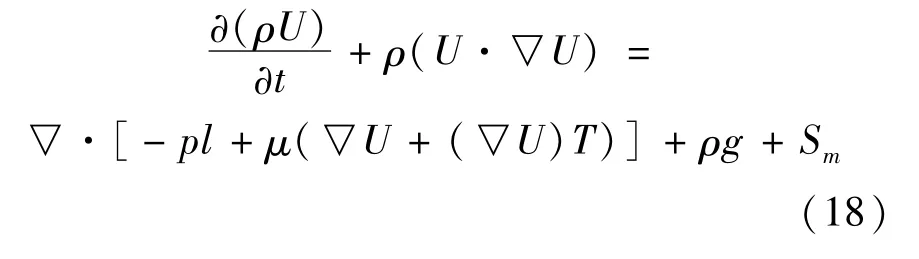
式中：Sm为电磁力、热浮力、流动阻尼力等体积源项。

熔体流动过程中往往伴随着热交换，使得熔体温度不断变化。因此研究流场的同时，必须考虑熔体的传热。根据傅里叶传热与能量守恒定律，可得到流体传热的能量守恒方程。

描述传热过程的基本方程：

式中：Q为热源项。

金属凝固传热通常分为单个域与多个域两种方法。焓-多孔介质模型[32-33]是一种能较好地模拟流动与凝固传热的单域模型，其考虑了糊状区内潜热释放与流动，收敛性较快，并且与试验结果[34]吻合较好。这与Bennon 的连续模型[35]和Beckermann的体积平均模型[36]内容基本一致，为后续电磁场作用下熔体内流场与温度场的耦合模拟奠定了基础。多域模型[37]由于复杂的界面域网格重构而使用较少。

金属凝固过程中，糊状区同时包含柱状晶、等轴晶和液相，而柱状晶和等轴晶会阻碍金属液在糊状区的流动，进而影响金属的传热与凝固过程。一般采用变黏度法[38-40]和达西源项法[41]处理糊状区的流动。

2.1 变黏度法

Roplekar等[42]基于体积平均模型，结合潜热回升-混合长度模型研究了旋转磁场下铝合金半连铸过程中的宏观偏析现象，并进行了试验验证。将式（18）中的熔体黏度μ写成涡流黏度μt与分子黏度μ0之和，其表达式分别为：

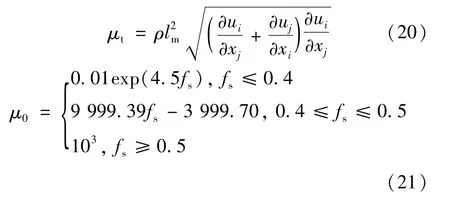
式中：lm表示湍流中液滴混合或碰撞的平均自由程，且lm＝ min（0.435ln，0.09lc），其中ln为距最近壁面的距离，lc为特征长度，本文取圆柱结晶器的半径；fs为固相率。μ0曲线如图3（a）所示。

Kumar等[38]在模拟电磁搅拌条件下铝合金半连铸凝固过程的相变时，采用Flemings[43]测定的黏度数据（图3（b））代入方程。研究发现，半固态熔体在结晶器内受电磁力影响，壁面处熔体沿外壁向上运动，中心处熔体沿中轴线向下运动。由于电磁搅拌的作用，结晶器内温度分布更加均匀。

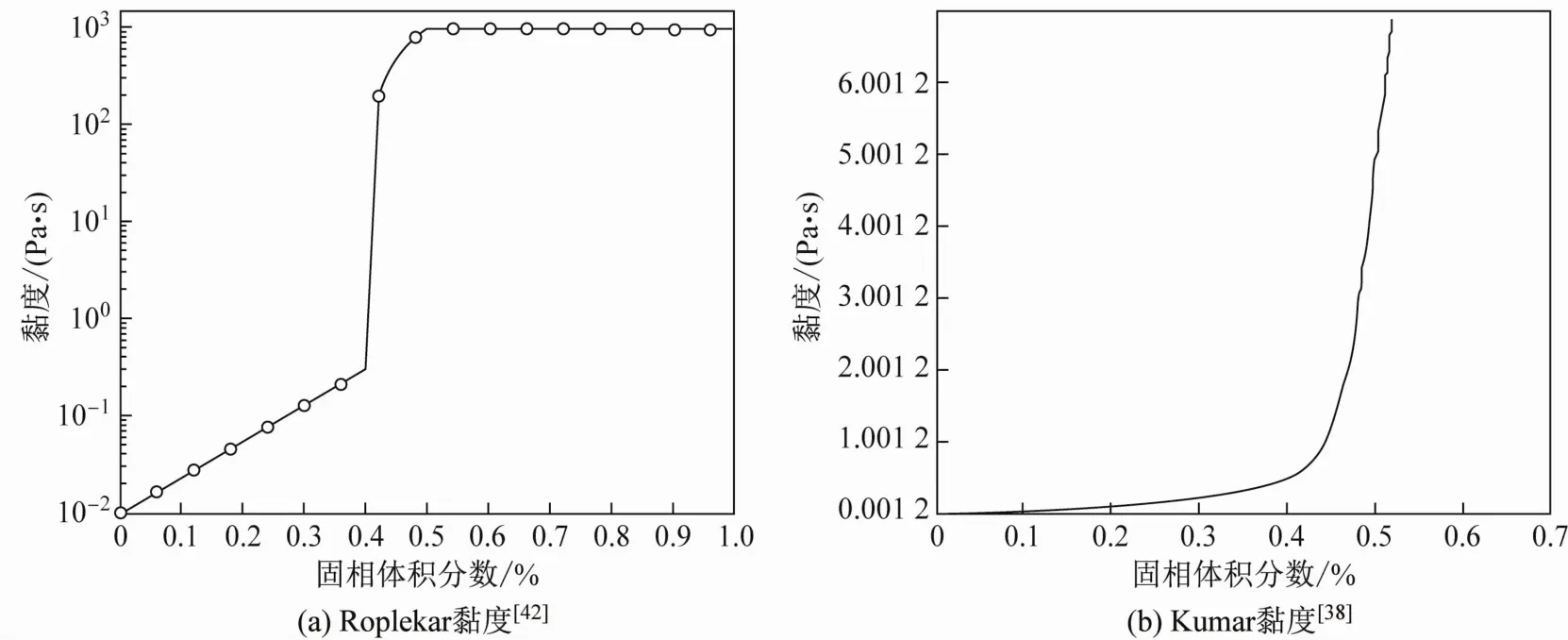
图3 黏度随固相率的变化Fig.3 Variation of viscosity with solid fraction

2.2 达西源项法

然而，黏度变化曲线往往很难获取，因此达西源项法的应用更为广泛。但学者对达西源项的表达式存在不同的意见[41，44-46]。目前常用的有一次枝晶臂间距法、二次枝晶臂间距法和经验值法。其中，大多数学者[36，47-49]依据Carman-Kozeny 方程通过枝晶臂间距确定多孔介质中的渗透率K，渗透率K与达西源项SD的关系为：

（1）一次枝晶臂间距法

Pfeiler等[50]根据Blake-Kozney 方程将达西源项写成如式（23）所示的形式，其中λ1为一次枝晶臂间距。在此基础上预测了结晶器内钢液的流动状况、凝固坯壳的生长和夹杂物在固/液界面的运动轨迹，并证明了直径大于一次枝晶臂间距的夹杂物难以被糊状区捕获。

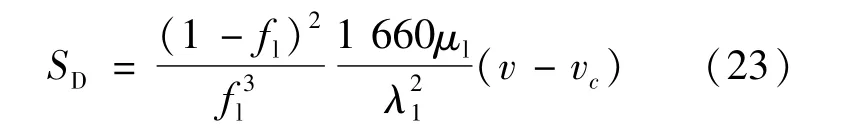
Ramirez等[47]分别对比了渗透率K两种不同计算方法的适用条件，如式（24）、（25）所示。而Gu等[51]则通过式（24）模拟研究了大型铸锭凝固过程中的流动、温度及物质浓度分布规律：

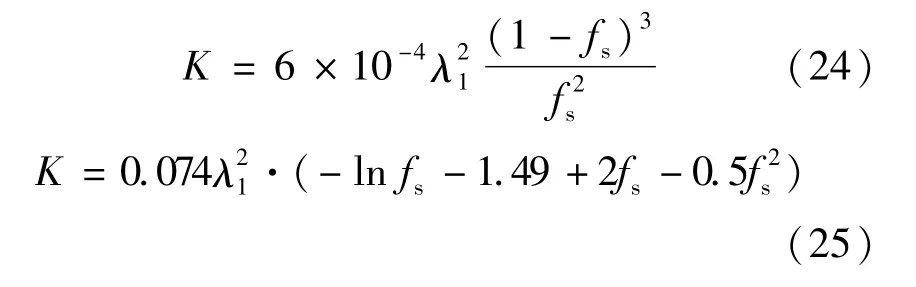
Aboutalebi等[52]利用式（26）模拟了拉速、钢种、水口结构对流型和凝固形态的影响，并与实测结果吻合较好。Willers等[49]根据该方法研究了旋转磁场下Al-Si合金在模铸条件下的凝固过程，发现提高变向频率能消除低频时熔体中磁场引起的温度波动现象。

（2）二次枝晶臂间距法

Zhang等[10]基于体积平均模型将焦耳热与凝固潜热加入能量守恒方程，利用达西源项处理糊状区流动问题。设为枝晶干涉临界固相率，令初始渗透率K0＝（dSDAS）2/180（dSDAS为二次枝晶臂间距）。表1为凝固不同阶段的黏度与渗透率。

表1 不同阶段的黏度与渗透率Table 1 Viscosity and permeability in the different stages

表1中，χ是使能量守恒方程收敛的较小正数；X为需要求解的变量；Xs表示固相中的对应变量。研究发现[53]，随着电磁场频率的增加，熔体流动强度先增大后减小，而温度场和熔池深度变化不大。

Jiang等[54]在多孔介质模型的基础上结合表观黏度模型，建立了电磁搅拌作用下连铸二冷区凝固行为与溶质传输模型；并对柱状晶区采用多孔介质模型，将等轴晶区视为浆体区，采用表观黏度模型模拟熔体流场。糊状区渗透系数K如式（27）所示。对等轴晶区内的钢液流动情况，采用μm替代式（18）中的μ，如式（28）所示：

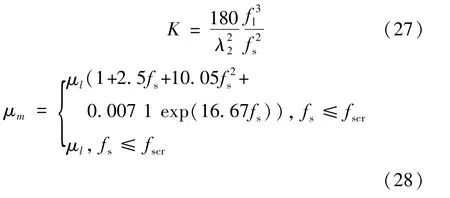
Sun 等[55]为了在式（27）的基础上增加一个较小的正数ξ，给出了二次枝晶臂与局部凝固时间的关系，如式（29）、（30）所示，并利用该方法模拟研究了M-EMS和F-EMS对高碳钢连铸方坯凝固过程与元素偏析的影响。通过连铸坯表面温度、EMS中心磁通量密度、铸坯形貌及溶质分布，验证了电磁场下连铸坯的凝固与偏析过程。

（3）经验值法

采用经验值处理达西源项时引入一个糊状区系数Amush：

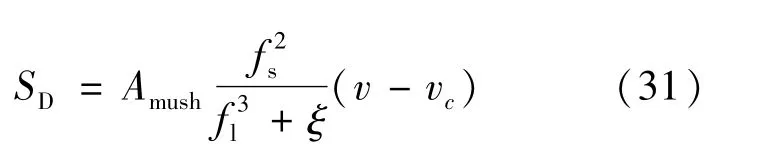
国内外学者[56-57]针对Amush对熔体流动的影响进行了探讨。Hietanen等[56]模拟大方坯连铸结晶器内钢液流动时发现，较小的Amush会导致钢液温度下降较快，而较大的Amush会导致模型计算不易收敛。而李少翔等[57]模拟大方坯连铸结晶器内的流动凝固行为时，发现随着糊状区系数的增大，糊状区宽度变窄，并给出了合理的糊状区范围为（1～5）×108。

Zhang等[58]利用式（31）结合拉格朗日法求解了小方坯结晶器内夹杂物的运动规律，该方法的计算结果与实测值基本吻合。Wang等[59]研究了板坯连铸中流动控制结晶器对坯壳生长的影响，并通过对比固液相线与实测坯壳厚度的变化曲线，验证了模型的可靠性。Sun等[60]研究了不同水口类型与M-EMS组合对结晶器内钢液流动及坯壳厚度的影响，其中Amush＝105。He等令Amush＝108，建立了3种类型的浸入式水口对结晶器内钢液流动的影响，并通过物理水模型验证了流场的可靠性。近几年将Amush代入达西源项模拟研究熔体的凝固过程[44，61-65]已成为一种趋势。

除了在连续铸钢中的模拟应用外，东北大学乐启炽团队利用该方法建立了脉冲磁场下镁合金半连续铸造的连续介质模型，其中Amush＝105。研究发现，差相脉冲磁场作用下的z向电磁力与z向流速均大于一般脉冲磁场下的，从而导致了更强的对流、更加均匀的温度分布以及更加细化的组织[66]；同时也分析了电磁力、电流峰值、电压占空比及频率对熔体的影响，发现电流增大，熔体流动性增强，导致熔体热量散失，熔体温度和熔池深度均降低；频率的增加则不会引起多大变化；占空比的增加仅对电磁力有所增益[67]。

3 总结与展望

本文介绍了电磁场数学模型、流场与温度场耦合模型在电磁场处理金属凝固过程中的建模与应用。总结了求解电磁场空间分布的部分算法模型，其中矢量势求解法主要应用于时变感应电磁场，可直接用于解决脉冲、谐波等瞬变电磁参数问题；直接求解法一般采用Biot-Savart定律对电流产生的磁场求解，适用于解决直流电等恒定电磁参数的问题，或者先将瞬变信号转化为等效的恒定信号再求解计算，具有一定的局限性。接着介绍了电磁场作用下流场与温度场的耦合模型，以基于单域模型的体积平均模型为主，阐述了不同的糊状区处理方法，其中添加达西源项的方法应用较为广泛，但对达西源项系数的取值仍存在不同意见；此外，将糊状区黏度处理为不同形式的函数也是解决方法之一。

目前已能够相对准确地预测电磁场作用下的熔体演变过程、温度分布、坯壳生长以及金属液受电磁力驱动的强制对流流场分布等，但大多仍是基于试验数据而展开的。将更多的物理场耦合在一起，建立不同空间尺度与时间尺度的数值模拟，并应用于实际工业环境，仍然是个巨大的挑战。