焊缝余高及缺陷对管道环焊缝漏磁检测的影响

郝大洋，饶连涛，刘觉非，苏 林，成文峰，徐 杰

(1.中国矿业大学 材料与物理学院，徐州 221116；2.管网集团(徐州)管道检验检测有限公司，徐州 221008)

管道运行安全是管道行业的立足之本，通过各类检测技术及时发现和修复管道缺陷是提升管道安全运行水平的重要手段。因此，提高长输管道的缺陷检测与评价水平对保证管道的安全运行尤为重要[1-4]。

在焊接过程中，受焊接参数调节不当等因素影响，焊缝处会出现凹坑、气孔、咬边、错边、未融合等表面缺陷，而这些缺陷正是导致管道开裂的主要原因。目前，常用的管道无损检测方法有涡流检测、磁粉检测、漏磁检测、超声检测等。由于漏磁检测具有检测灵敏度高、不需要耦合剂等特点，漏磁检测法已成为国内外应用最为普遍的管道无损检测技术之一[5-7]。

基于漏磁检测原理，借助COMSOL软件，采用轴向励磁方法对焊缝余高和凹坑缺陷处的漏磁场进行了三维仿真，得到了不同参数下的磁通密度径向分量和轴向分量分布曲线，着重探讨了管道环焊缝因余高存在导致的增厚型信号特征与不同余高时缺陷存在导致的减薄型信号特征，以及缺陷位置(管壁、熔合线和焊缝中心)对漏磁信号的影响，提出了增厚型缺陷和减薄型缺陷复合时磁通密度分布曲线的分析方法，为管道焊缝缺陷漏磁信号的特征识别提供了参考。

1 管道环焊缝及缺陷的有限元模型

1.1 几何模型

采用COMSOL有限元软件的电磁模块对管道漏磁检测进行仿真模拟，管道环焊缝的几何模型如图1所示，焊缝中心凹坑缺陷几何模型如图2所示。该模型中设管道径向为坐标轴x方向，轴向为坐标轴y方向，即Bx为磁通密度径向分量，By为磁通密度轴向分量。为便于比较分析，模拟计算的传感器提离值、磁化器提离值均取1 mm，即传感器、磁化器与管道内壁的距离均为1 mm。

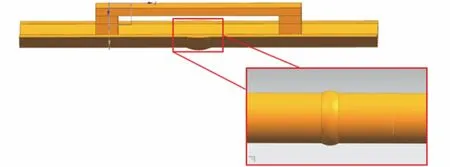
图1 管道环焊缝几何模型

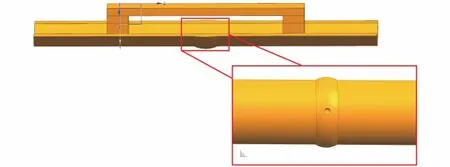
图2 焊缝中心凹坑缺陷几何模型

1.2 材料属性

由漏磁检测原理可知，模型中的关键部件有管道、管道外侧空气罩、励磁源、极靴、衔铁等，模型中需分别对每个关键部件的材料属性进行定义。

该模型中采用永磁体作为励磁源，设其矫顽力为8 960 kA·m-1，空气的相对磁导率为1.0。管道材料为Q235钢，在模拟过程中，为满足实际需求，对不同的部分采用不同的磁化方式，其中空气采用相对磁导率磁化，永磁体采用剩磁磁化，管道采用B-H曲线磁化[8]。

2 结果分析与讨论

2.1 焊缝余高对漏磁信号的影响

为了研究余高对漏磁信号的影响，取焊缝余高为0.5，1，1.5，2，2.5，3 mm，对不同余高下的磁通密度分布进行计算，得到不同余高下的磁通密度径向分量和轴向分量分布曲线如图3所示。

由图3(a)可知，焊缝处漏磁信号径向分量Bx呈现典型的一正一负两个峰，且对称分布于焊缝中心两侧。Bx峰值随着焊缝余高的增加显著增大，即焊缝的漏磁信号强度随着焊缝余高的增加而显著增强。由图4(b)可知，轴向分量By呈现一典型的凸峰特征，即一个波峰、两个波谷，且By凸峰的峰值和两侧的谷值亦随着焊缝余高的增加而增大。余高的存在相当于管道焊缝处壁厚增加，相较于管壁处缺陷的减薄，余高的漏磁信号呈现典型的增厚特征，且余高越高，漏磁信号越强[9]。

余高约2 mm的实际管道环焊缝处漏磁信号(牵拉试验结果)如图4所示，可见，模拟得到的焊缝处漏磁信号与实际信号特征非常吻合，进一步验证了有限元模型的准确性与可行性。

图4 实际管道环焊缝处漏磁信号

为了进一步分析不同焊缝余高下的漏磁信号特征，分别对不同焊缝余高下径向分量Bx的峰峰值Bx_p-p(见图5)和轴向分量By的峰谷值By_p-p(见图6)进行了比较。可以看出焊缝余高小于2 mm时，Bx_p-p和By_p-p均与余高成近线性关系；超过2 mm时，随着余高继续增加，Bx_p-p与By_p-p非线性增大，且增加速率逐步放缓。

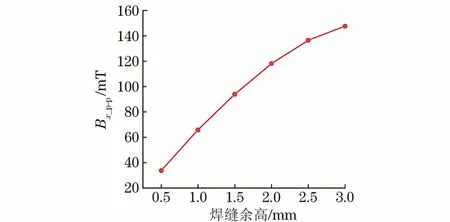
图5 不同焊缝余高下Bx峰峰值Bx_p-p

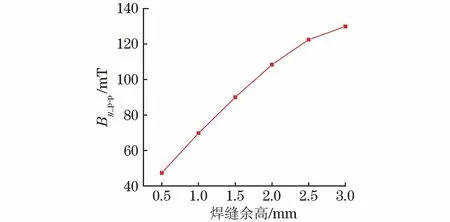
图6 不同焊缝余高下By峰谷值By_p-p

2.2 焊缝中心缺陷深度对漏磁信号的影响

对于焊缝中心缺陷，为了便于比较分析，将缺陷简化为椭球体，设椭球体短半轴沿管子轴向长度方向尺寸不变，均为2.5 mm；长半轴沿管子径向，即壁厚方向的尺寸为缺陷深度。为了研究不同余高下(13 mm)不同凹坑缺陷深度对漏磁信号的影响，笔者设计了相同直径、不同深度的9种椭球型缺陷，即取凹坑深度分别为壁厚t的10%，20%，30%，40%，50%，60%，70%，80%和90%(管道壁厚t为10 mm)，计算不同深度下的漏磁场分布。

焊缝余高为1，2，3 mm时，不同深度椭球形缺陷磁通密度分布曲线如图7，8，9所示。

图7 余高1 mm时不同深度椭球缺陷磁通密度分布曲线

由图7可知，与以往管道单一缺陷的漏磁信号相比，焊缝处缺陷的磁通密度分布曲线发生了明显的复合现象。以往研究表明，轴向励磁条件下，管道缺陷漏磁信号的径向分量Bx分布曲线表现为典型的先负后正极性相反(减薄型)的两个中心对称峰[10-11]。由图7(a)可知，焊缝缺陷的漏磁信号表现为外侧先正后负的两峰中间夹着内侧的先负后正的4个对称分布的复合峰；而轴向分量By分布曲线则表现为外侧凸峰中间夹着一个凹峰[见图7(b)]。对该结果进一步分析可知，焊缝余高所产生的信号上叠加了缺陷的漏磁信号，从而导致磁通密度分布曲线发生复合，且随着缺陷深度增加，曲线的复合现象越明显，如径向分量Bx的外侧峰(焊缝余高漏磁信号)峰值逐渐降低，而内侧峰(焊缝缺陷漏磁信号)的峰值增加。因此，可以根据曲线的复合程度初步判定焊缝上是否存在缺陷。

由图8可知，当焊缝余高为2 mm时，不同深度椭球缺陷磁场分布的径向分量Bx分布曲线和轴向分量By分布曲线与焊缝余高为1 mm时的分布曲线类似，但二者所能检测的缺陷深度范围明显不同，即相同缺陷时，随着余高增加，内侧峰的漏磁信号整体变小，磁通密度分布曲线的复合程度变弱，这里仅能分辨出深度大于80%壁厚缺陷的漏磁信号特征。此外，由牵拉试验结果可知，当余高达到2 mm时，焊缝中心仅深度大于80%壁厚的缺陷被有效检出，其余均未被检出，这与模拟结果吻合。

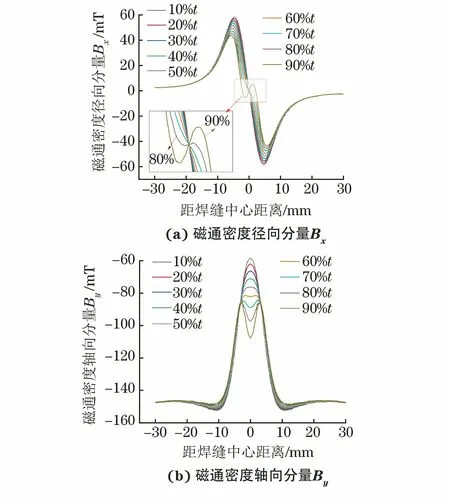
图8 余高2 mm时不同深度椭球缺陷磁通密度分布曲线

由图9结果可以看出，当焊缝余高为3 mm时，磁场分布的径向分量Bx分布曲线和轴向分量By的分布曲线均未见明显复合。因此，无法根据曲线的复合有效判定焊缝上是否存在缺陷。

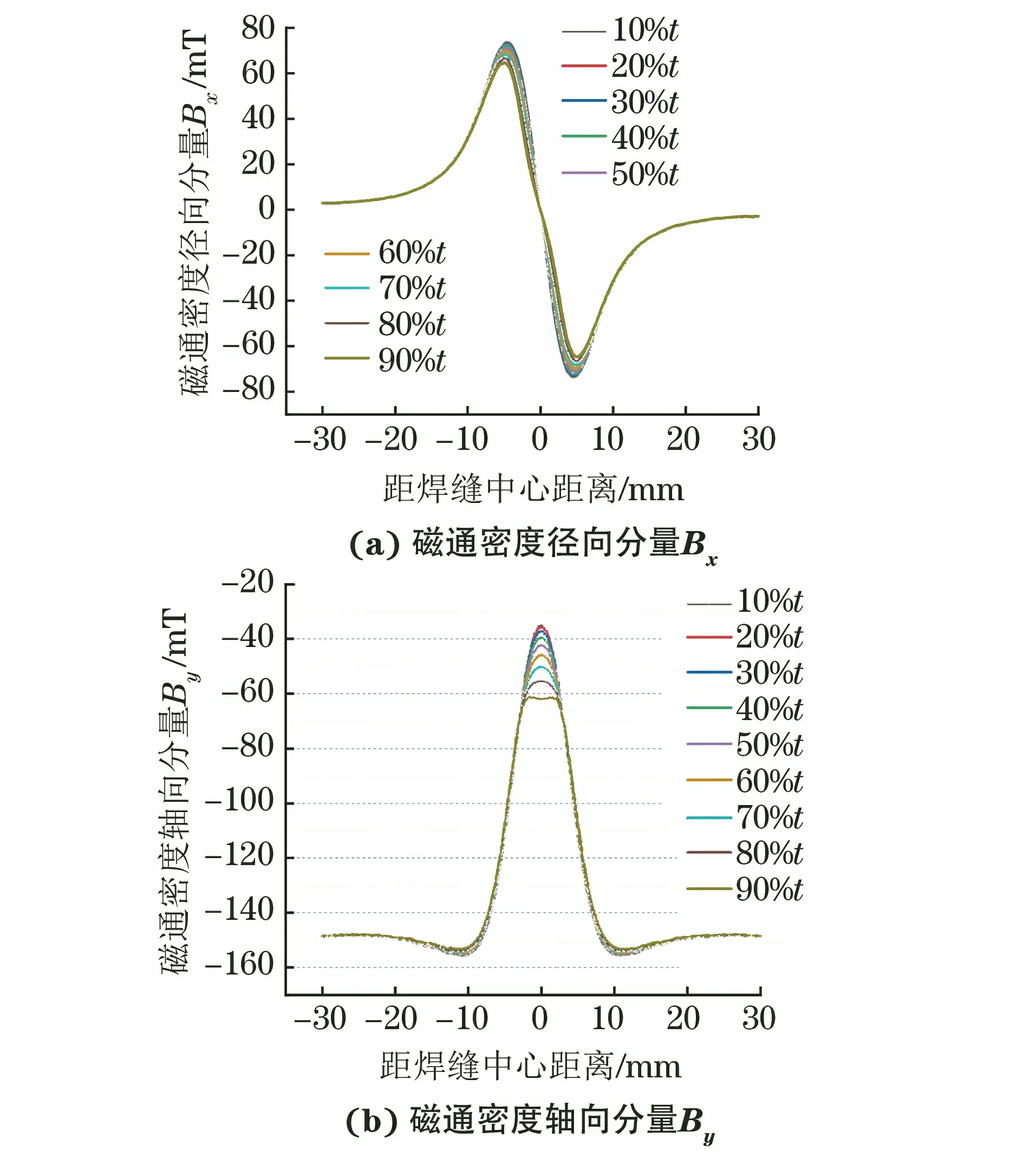
图9 余高3 mm时不同深度椭球缺陷磁通密度分布曲线

综上所述，当焊缝余高增加时，根据曲线的复合程度去判断焊缝上是否存在缺陷的有效范围变小，即随着焊缝余高的增大，焊缝上可有效检测到的缺陷最小深度增大，这说明焊缝余高越大，同样的缺陷越不容易被检出。因此，焊缝上的缺陷能否有效检出与焊缝余高密切相关。

不同焊缝余高下Bx曲线外侧峰峰值Bx_p-p(即焊缝余高导致的漏磁信号)如图10所示，不同焊缝余高下焊缝中心区域峰值By_p-p如图11所示。由图10，11可知，焊缝余高相同时，随着缺陷深度增加，Bx外侧峰峰值减小，焊缝中心区域峰值By也减小；缺陷深度相同时，随着焊缝余高的增大，Bx峰峰值增大，焊缝中心区域峰值By也增大。

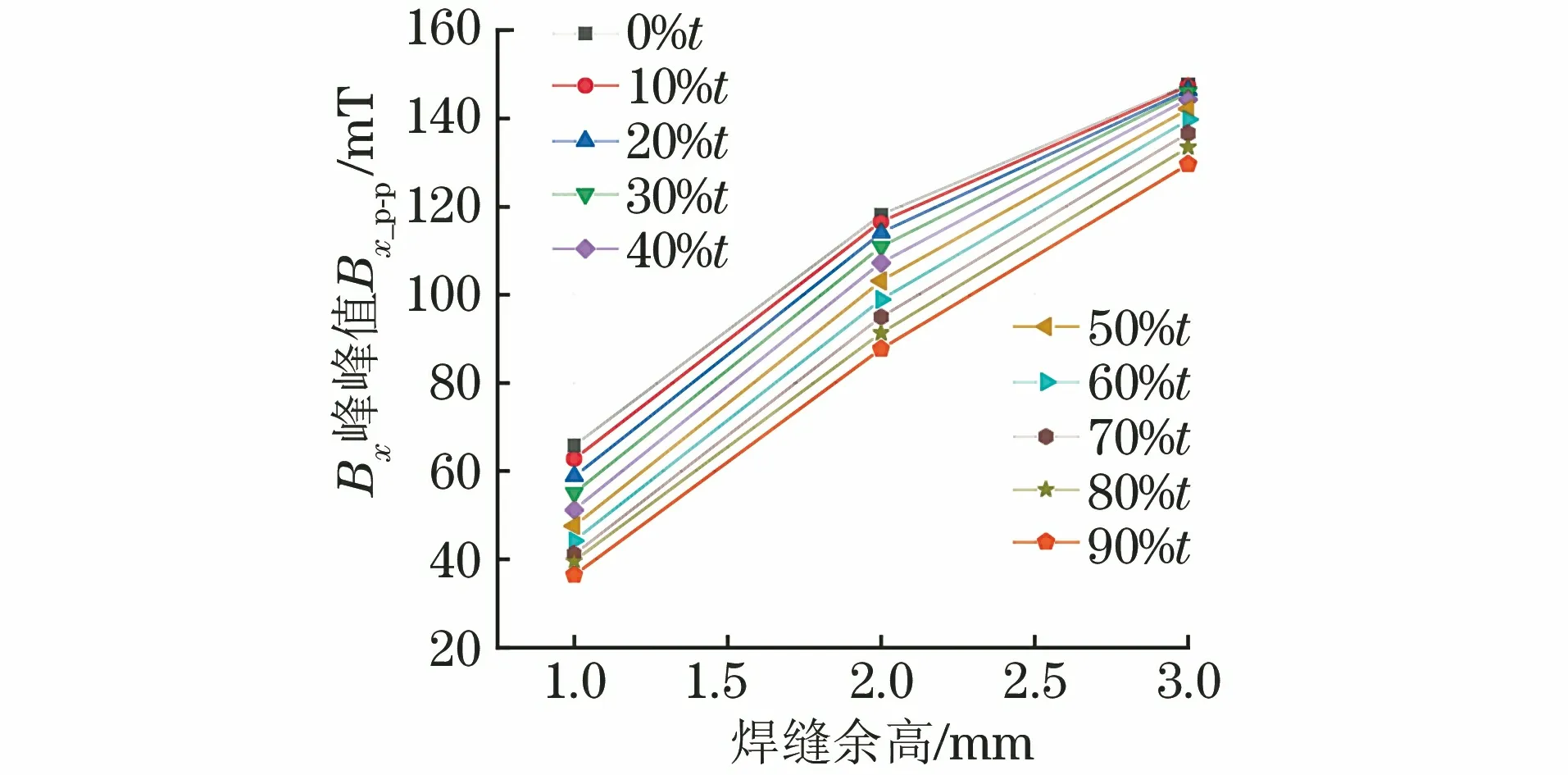
图10 不同焊缝余高下Bx峰峰值Bx_p-p

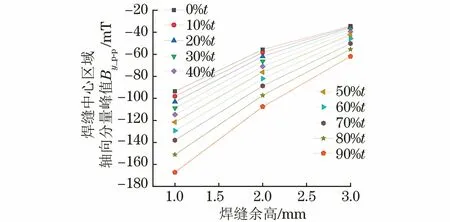
图11 不同焊缝余高下焊缝中心区域峰值By_p-p

为了进一步分析复合漏磁信号的特征，对焊缝余高为1 mm,凹坑深度为50%壁厚和焊缝余高为1 mm无缺陷时的磁通密度分布曲线以及两者的相减曲线进行比较，结果如图12所示。可见相减曲线呈典型的减薄型缺陷漏磁信号特征，进一步证明了焊缝余高与中心缺陷磁通密度分布曲线的复合现象。

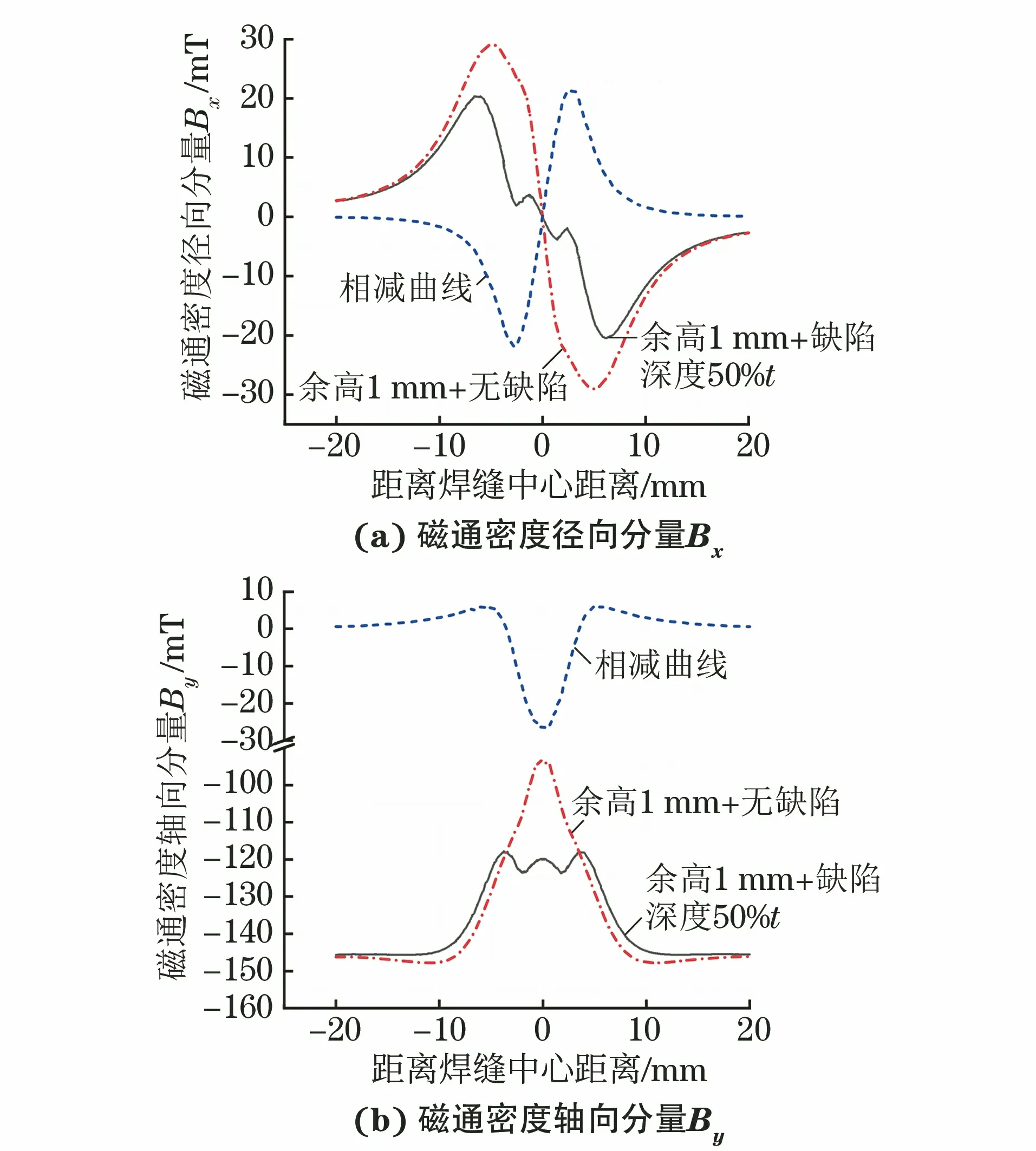
图12 焊缝有、无缺陷时磁通密度分布曲线及其相减曲线

2.3 不同位置椭球缺陷的漏磁信号分布特征

根据牵拉试验样管中的缺陷制备方案，相同椭球凹坑处于不同位置时的几何模型如图13所示，分为3种典型情况：管壁(左侧红色凹坑)，熔合线(中间绿色凹坑)，焊缝中心(右侧蓝色凹坑)，不同位置缺陷的磁通密度分布曲线如图14所示。

图13 相同椭球凹坑处于不同位置时的几何模型

由图14可知，由于所处位置不同，相同缺陷的漏磁信号存在较大差异。其中缺陷位于管壁时的漏磁信号最强，而在焊缝中心时的信号最弱，位于熔合线时的信号强度则介于两者之间。该结果说明焊缝中心缺陷相较于其他位置的缺陷更难被检测出来。后进行牵拉试验，共预制12个圆柱形凹坑缺陷，凹坑直径为8 mm,位置分别为近焊缝、熔合线和焊缝中心处，其中19号缺陷检出，1012号缺陷未检出，这与有限元模拟的结果是一致的(见图15)，即缺陷位于焊缝中心时的检测率最低。

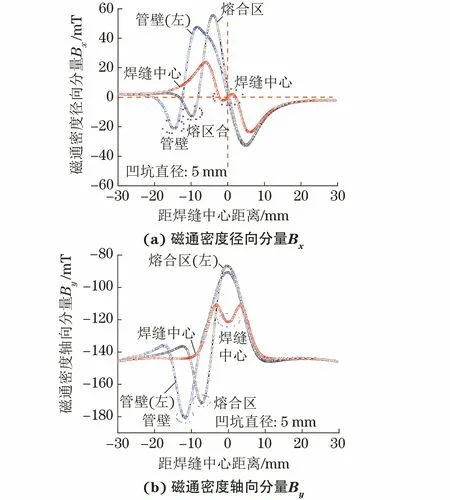
图14 不同位置的缺陷磁通密度分布曲线

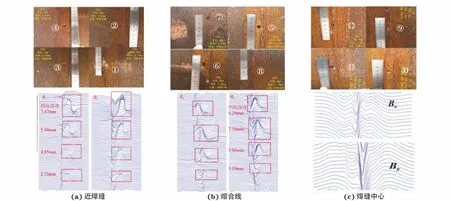
图15 牵拉试验结果

3 结语

采用COMSOL软件对不同余高下焊缝中心凹坑缺陷漏磁场分布特征进行了仿真模拟，同时开展了牵拉试验，得到了以下结论。

(1) 随着焊缝余高增加，磁通密度径向分量、轴向分量的峰值均非线性增大。通过牵拉试验测试结果与模拟结果的对比，验证了有限元模型的准确性与可行性。

(2) 对于焊缝中心椭球凹坑缺陷，不同余高下可检测出缺陷的尺寸范围不同。随着焊缝余高的增大，可检测出的缺陷最小深度增大，即相同尺寸的缺陷，焊缝余高越大，越难被检测出来。因此，焊缝余高的存在及其大小是决定焊缝上缺陷能否被检测出的关键因素。

(3) 不同缺陷位置漏磁信号的分析表明，相同缺陷在管壁处、熔合区、焊缝中心处的漏磁信号强度依次减弱，进一步说明同样的缺陷在焊缝中心时最不易被检出，该结果与牵拉试验结果一致。