浅谈新课程理念下如何上好数学试卷讲评课

刘 静

(淮北市海宫学校 安徽淮北 235000)

一、初中数学试卷讲评课学情分析

(一)内容

试卷讲评课学情分析内容应按照学生的基础及学习情况进行确定，首先将学生解题的错误类型进行分类，然后再根据原因分类的标准，针对学生的学习情况进行比较研究，以便确定教学起点。比如基础较好的学生的错题致错原因有哪些，后进生做错题的原因有哪些，错误产生的原因因人而异，不能一概而论。此外还可以通过数据法对易错试题进行研究，检查易错试题所占比例是否异常，是否应作为教学重点，等等。

(二)目的

试卷讲评课属于复习课程，首要的教学目标是对学生答题中的错误之处进行纠正，找出答错的原因，寻求正确的解法，提高学生的答题正确率。在此之前，了解学情可以帮助教师了解学生产生问题的根本原因，以便反省自身教学方法，须知教学是一种双向互动的过程，之前知识课上的教学方法，不一定能够满足所有学生的学习需求。因此，通过试卷讲评课把握学情，能够使教师有针对性地审视知识课的教学效果，对教学过程进行补充，在讲评课上针对学生容易出现的错误进行改正，达到师生共同进步的目的。

二、新课程理念下如何上好数学试卷讲评课

(一)适时开展讲评课

试卷讲评课具有时效性，考试结束后是学生最为关心成绩的时刻，然而在学生还面临其他科目考试时，不应泄露讲评内容、学生成绩、试题答案等备课内容，以防影响考生心态。但考试后的试卷讲评课不宜滞后，否则讲评效果会大打折扣。教师应在全部考试结束后安排讲评课，在学生保留解题记忆时进行讲评，效果会翻倍。

(二)突出学生的主体性

考试过程是学生主体性思维活跃的过程，是学生数学知识的选择与运用的过程，因此在试卷讲评课中教师也要重视学生的思维梳理过程。如何面对具体问题具体分析和总结，这也是教师跟学生交互探讨的渠道。学生为什么概念掌握不清、知识应用不合理、解题方法不当，为此，教师应在讲评课中进一步摸清学生心理，让学生在引导中自觉走上合理化的道路，并对自己的错误足够重视，使学生在讲评课中树立主体意识。

(三)激励效应

试卷讲评课中适宜将错误的解题方法、思路及其形成原因向学生讲解说明，但应注意满足学生的求知欲望和积极性，只讲错例不点名，不能将思维的问题归结到个人身上，教师要教会学生能正确地认识自我，激发学生学习数学的积极性。

(四)体现数学思想

初中数学考试得分率较低的一个主要原因是学生的基础知识虽然牢固，但运用起来不够熟练，学生缺乏数学思想。因此，教师应以讲评课为契机，向学生传递一种数学思想，归纳总结、对比分析本身就是一种数学思想，讲评课中最应体现的就是数学思想，列举易错内容的教学目的是防止学生重复犯错，帮助学生重新梳理数学知识，如在讲解某道题时与以前练习过的试题做比较分析，对比两个题型的异同，使学生在对比研究中提高实际解题能力。

三、新课程理念下初中数学试卷讲评课教法研究

(一)讨论法的运用

试卷讲评课中的讨论法适合于脱稿应用，教师选择一些不依赖视觉判断逻辑的题目进行延伸讲解，在课堂上与学生们良性互动，舒缓教学节奏。例如，在考点“众数与中位数”中，不针对试卷上的习题，而由教师脱稿发起“苏沃洛夫式提问”：一组数据2、5、6、0、6、1、8的中位数和众数分别是什么？考查学生随机应变的能力，没有纸面呈现的既视感，全凭记忆力与临场反应，引导学生将一列数据按照记忆，由小到大进行排列，可发现5排在最中间，而6则出现了2次，因此答案也就在学生们的讨论与抢答中得到展示。有关众数与中位数的考点试题一般都是选择题，运用讨论法进行讲解，将课堂主动权还给学生，试题无须演示与研究，同时教师也获得了学生们的注意力集中趋势的即时情况，判断学生是否出现疲态，以此判断教学节奏是否应该舒缓，学生是否应该获得短暂的休息时间。

(二)讲授法的运用

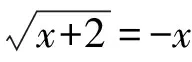
(三)分组研究法的运用

比如证明题，在展现证明过程时要求有一定的逻辑架构，这属于知识综合运用。虽然解题手段多种多样，毕竟在知识工具的使用顺序上，有较为固定的搭配，部分学生直接找到了准确路径，部分学生思维混乱，多头并举仍寻求不到结果，还有部分学生“偶然”证明到了结果，但不能保证下次遇到此类题型还可以得分。这种一题多解的数学题由于思路不统一，没有固定套路。例如四边形中，∥，=，是对角线上一点，且=，如果=，且∠∶∠=2∶3，求证四边形是正方形。本题考查正方形的判定定理，此类题目既开放又严谨，由于正方形具有平行四边形、矩形、菱形的一切性质，因此只要证明其是具有特殊性质的平行四边形、矩形或菱形之一即可，学生出现错误是因为多管齐下导致思维混乱。可以从证明△与△相等的方向入手，利用平行线判定定理，也可以从三角形内角和定理入手，运用“百花齐放”的分组研究法，利用教学时间，将学生分成若干小组，进行多角度讨论，在讲评课上碰撞出不一样的逻辑思维的火花。

结语

初中数学试卷讲评课既要充分进行课前学情分析，还要运用科学的教学方法，重视学生的主体地位，不批判，不揭短，以过程验证结果，注意保护学生的自尊心，激发学生的主动性，帮助学生建立起正确的逻辑体系，这样才能收到良好的教学效果。