纤维在转杯和输纤通道中的运动模拟
杨瑞华, 何 闯
(江南大学 a.生态纺织教育部重点实验室; b.纺织科学与工程学院,江苏 无锡 214122)
转杯纺是气流纺纱的一种,探究转杯纺纱通道中纤维的运动状态,对于阐明转杯纺纱机理具有重要意义。近年来有许多研究者对其他成纱方法中气流的纤维运动特征做了相关的研究,其中Jeffery[1]首次把纤维的物理模型看做刚性椭球,模拟了剪切流中纤维的运动;Smith等[2]把纤维模型看做由球和杆组合而成,并模拟了纤维在层流中做变速运动;Yamamoto等[3]建立纤维的物理模型,把纤维看做由n个半径为a的球体组成,并赋予纤维模型弯曲、拉伸特性;朱泽飞等[4]把刚性粒子当做纤维的物理模型,模拟了纤维在气流中的运动状态。这些研究为建立纤维运动模型提供了良好的研究背景,但转杯纺成纱过程中纤维在高速旋转转杯内的高速气流场内成纱,纤维运动特征决定了成纱结构和性能,对纤维在成纱器内尤其转杯内复杂运动的研究还有待深入[5]。本文在EDEM 2018中建立由若干个刚性小球连接形成的纤维模型,并通过建立Fluent-EDEM耦合分析模型,实现纤维模型在转杯纺纱通道气流场中的运动模拟,创新性地采用流固耦合方法研究柔性纤维在高速旋转转杯内气流场中的运动特征,为深刻理解转杯纺成纱机理提供基础,进一步优化成纱机构理论依据。
1 模型建立
1.1 转杯纺纱通道模型
通过SolidWorks 2018建立抽气式转杯纺纱通道模型,转杯直径为54 mm,凝聚槽类型为T型,如图1所示。同时在计算流体动力学(CFD)中划分网格,建立Fluent-EDEM耦合分析模型。
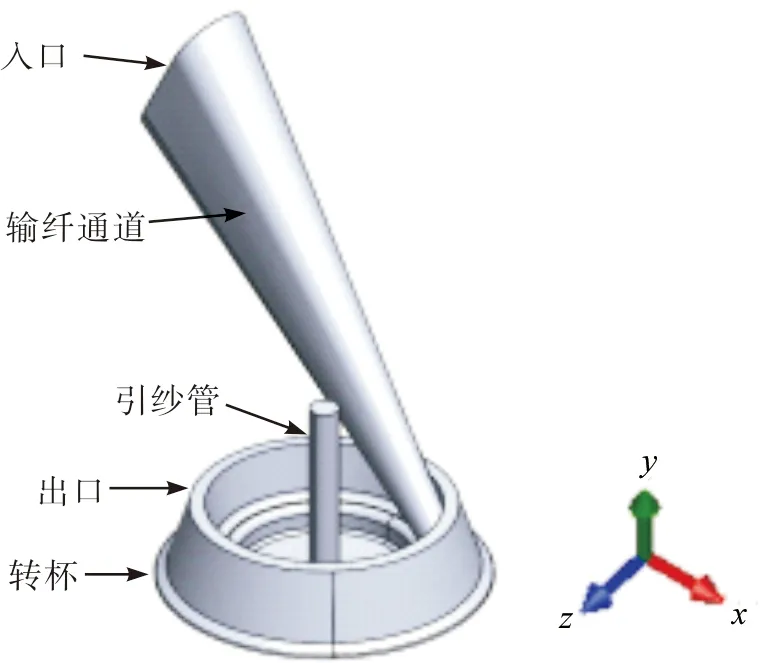
图1 转杯纺纱通道模型
1.2 气流场物理模型
转杯纺纱通道中的气流为湍流流动[6-8],模型满足能量守恒与动量守恒。
能量守恒:
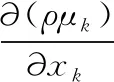
(1)
动量守恒:
(2)
(3)
式中:μk为沿xk方向的湍流黏性系数,uk为气流速度在xk方向的分量;ui为气流在xi方向的速度矢量,uj为气流在xj方向的速度矢量;ρ为气流密度,P为压强;τij为雷诺应力,δij为Komecker delta函数。
Fluent中的转杯纺纱通道的气流场模型选用标准k-ε湍流模型,如式(4)~(5),并运用Simple算法求解[9-10]。EDEM 2018中选用Hertz-Mindlin(No Slip)模型,如式(6)~(9)[11]。
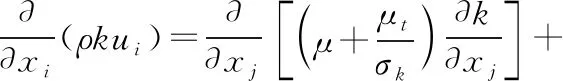
(4)
(5)
式中:ρ为气体密度,xi、xj分别为沿i、j的方向,ui为气流在xi方向的速度矢量;μ为湍流黏性系数;Gk为层流速度梯度产生的湍动能;Gb为浮力产生的湍流动能;YM为对总耗散率的影响因素;σk和σε分别为湍流动能k与耗散能ε对应的普朗特数;C1ε=1.42、C2ε=1.68、C3ε=0.09。
法向力:
(6)
(7)
切向力:
Ft=-Stδt
(8)
(9)
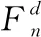
1.3 纤维模型及边界条件
输纤通道进口速度为50 m/s,转杯转速为50 000 r/min,出口压强为-8 000 Pa,引纱口压强为0 Pa,如图2所示。
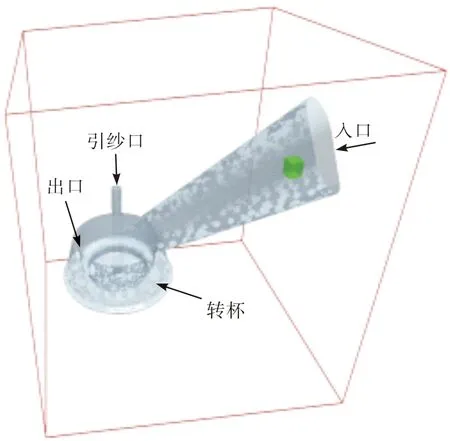
图2 转杯模型的边界条件
假设纤维模型以棉纤维为原型,根据FZ/T 01101—2008(2015)《纺织品 纤维含量的测定 物理法》纤维密度表可知,密度取1.54 g/cm3,细绒棉细度分布为1.43~2.22 dtex,这里纤维线密度取2.12 dtex,杨氏模量为300 MPa,分梳辊转速为5 000 r/min,分梳辊直径为65 mm,条子定重为18 g/10 m(1 800 tex),所纺目标纱线为10S(58.31 tex)的纯棉纱,根据《棉纺手册》表3-9-22转杯纺纱线推荐捻系数表可知,捻系数分布在350~450,本文设计捻系数取350,即458捻/m。
通过以上计算可知,输纤通道中来自分梳辊的纤维约30根,由于纤维在纺纱通道气流场中的运动属于流固耦合问题的研究,研究流固耦合的方法有拉格朗日法和欧拉法:采用拉格朗日法将纤维作为离散相,把纤维简化为离散颗粒,模拟计算各个纤维颗粒在气流场中的运动分布特征,颗粒长度取1 mm;采用欧拉法将气流场视为连续相,探究纤维颗粒在纺纱通道气流场中的运动规律。中国的棉花标准规定当主体长度不大于30 mm时以16 mm为短纤维的界限,为使纤维模型更接近真实情况,进一步探究纤维的运动特征,本文纤维长度选取16 mm。纤维长度分别选取1 mm和16 mm,EDEM中共计产生30根纤维,纤维由多个刚性小球连接,纤维物理模型如图3所示。

图3 纤维物理模型
2 纤维运动模拟分析
为了研究纤维在转杯纺纱通道内的运动分布规律,本文模拟了长度为1 mm的纤维在输纤通道和转杯内的运动情况,探究了长度为16 mm的纤维在输纤通道中的运动分布过程。
2.1 输纤通道内气流的压强与速度分布
为探究输纤通道内压强的分布规律,本文取Z=8.5 mm处的截面,如图4(a)所示。在输纤通道截面“入口-出口”处做辅助线AB,提取AB上的压强数值作曲线,如图5所示。由图4(b)可得,输纤通道入口到出口,压强不断降低,从曲线斜率得出,越靠近出口压强减小的速率越快,入口处的压强为+591.6 Pa,出口处的压强为-7 400 Pa,这样的压强差有利于纤维的伸展及向转杯内输送纤维。
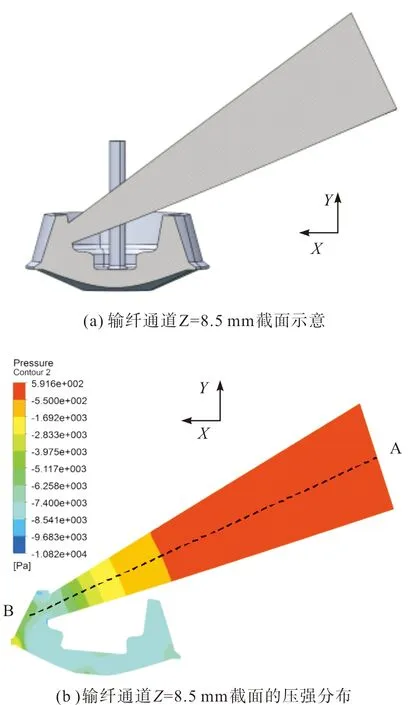
图4 输纤通道内压强分布
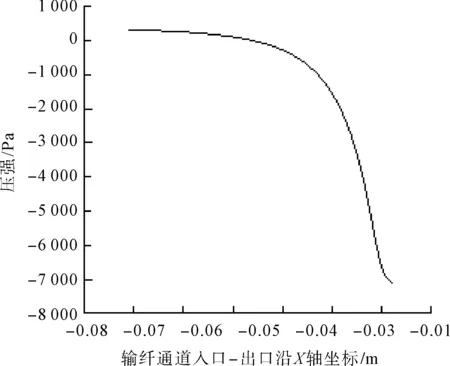
图5 输纤通道Z=8.5 mm截面上AB线段上的压强分布
由图6可知,输纤通道中气流的速度分布并不均匀,呈速度梯度状分布。提取输纤通道截面上线段CD的气流数值,作曲线(图7)得出,输纤通道内的气流做变加速运动,越靠近出口速度越大,在输纤通道出口处气流速度达到最大值118.4 m/s,随后与转杯滑移面碰撞,速度略有降低。
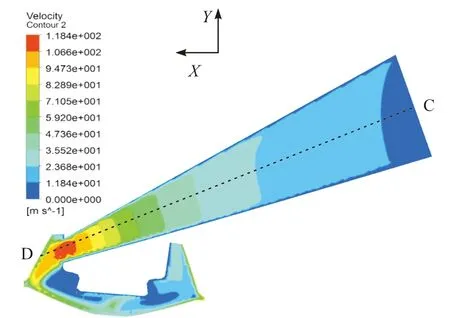
图6 输纤通道Z=8.5 mm截面的速度分布
2.2 1 mm纤维在输纤通道内的运动模拟分析
图8展现了长度为1 mm的纤维在输纤通道中的运动状态。在图8(a)中,纤维间的形态较为密集,从速度标尺可知纤维的速度相同,这是由于纤维刚进入输纤通道,气流对纤维的影响较小,纤维间的速度分布较为均匀。在图8(b)~(d)中,纤维在输纤通道中做加速运动,纤维在t=0.000 3 s沿着输纤通道下壁面运动,在t=0.000 5 s时纤维间的形态较为分散,这是因为越靠近输纤通道出口的位置,气流的压强梯度和速度梯度变化越快(图4、图6),从而使得纤维间的速度差增大。t=0.000 7 s时,由于输纤通道的渐缩结构,越靠近出口横截面越小,纤维又紧贴着输纤通道下壁面运动。在图8(e)中,纤维完全流出输纤通道,一部分纤维与转杯滑移面接触,由于与滑移面的碰撞,纤维速度较上一时刻有所降低。各时间段的纤维速度分布如表1所示,在时间t=0.000 1 s纤维速度最小为25.1 m/s,t=0.000 7 s纤维速度最大为84.2 m/s。
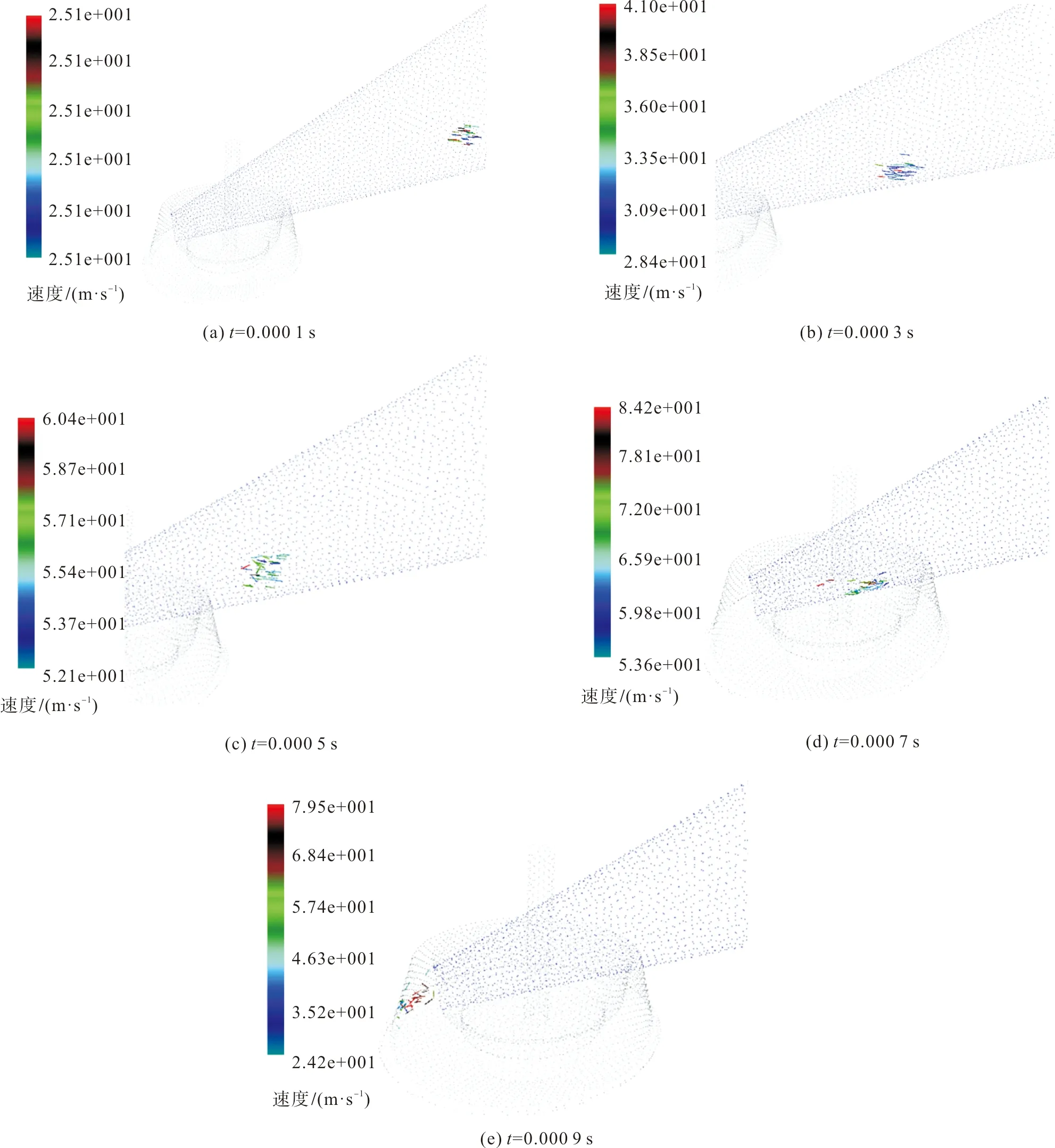
图8 纤维在输纤通道的运动分布

表1 1 mm纤维在不同时刻的速度分布
2.3 1 mm纤维在转杯内的运动模拟分析
纤维进入转杯凝聚槽内,随着转杯一起旋转运动,并在凝聚槽内纤维围成圆圈形状。这是由于纤维从输纤通道进入转杯后,与转杯滑移面接触后滑入凝聚槽内,随着凝聚槽内纤维根数的增加,最终形成一定线密度的须条,经加捻盘加捻后,通过引纱管引出纱线。
由图9可知,纤维速度分布在85.9~89.6 m/s,输纤通道出口与转杯滑移面交接处纤维的速度相对较低,速度分布为85.9~86.7 m/s,如圆圈①处所示。这是由于纤维从输纤通道流出后与滑移面发生碰撞,碰撞后的纤维发生形变,一部分动能转化为弹性势能,使得纤维速度降低,随后纤维又被高速旋转的转杯逐渐加速至89.6 m/s,如圆圈②处所示。由图10可知,纤维在转杯凝聚槽内速度矢量方向一致,与转杯转向相同。如图11所示,30根纤维中速度分布不均,是由于在高速旋转的转杯中,气流分布并不均匀,气流的速度也大小不一,这就会导致受到气流裹挟的纤维的速度不同。故在气流纺纱过程中,要保证纱线质量,首先要保证转杯纺纱通道中稳定的气流场,有利于提高成纱稳定性,减少断头。如图12所示,大部分纤维的角速度与转杯转速(300 000 deg/s)相同,其余纤维的角速度分布在299 500~299 900 deg/s。纤维之间的角速度差,进一步说明了纤维在高速转杯内运动的复杂性。对纤维速度与纤维角速度做相关性分析,结果两者的皮尔逊指数为0.060,Sig.值为0.785。其中皮尔逊取值为-1~1,其值大于0说明正相关,小于0为负相关,本次分析值为0.060,说明两者正相关。其中Sig.表示显著性,其值大于0.050,不显著,在0.050~0.010为显著,小于0.010为非常显著,本次分析值为0.785,说明两者关系不显著,相关性低。

图9 纤维在转杯凝聚槽中速度分布

图10 纤维在凝聚槽中速度矢量图
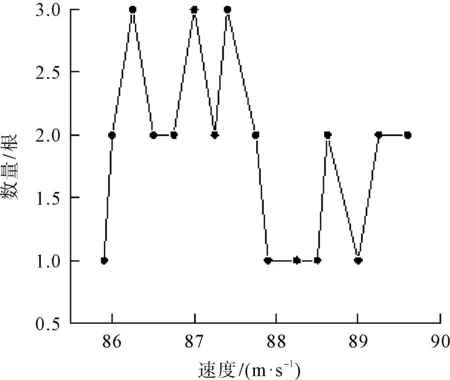
图11 纤维速度数量分布
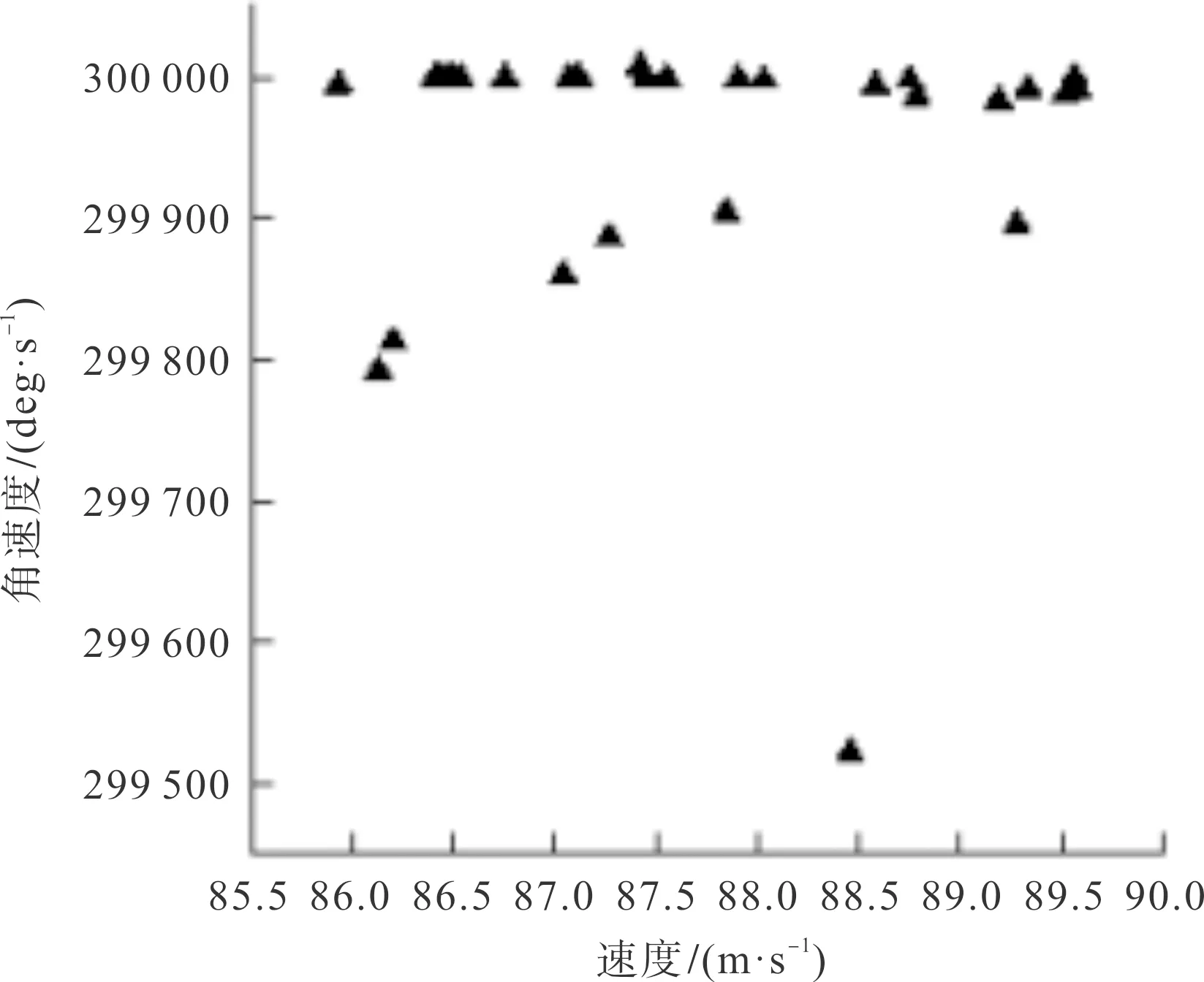
图12 纤维角速度纤维速度分布
如图13所示,30根纤维的转动动能分布在2.65×10-9~3.04×10-9J,纤维间转动动能的差异,是由于转杯内气流的不稳定性导致的。如图14所示,大部分纤维的转动动能为3.04×10-9J,其余纤维的转动动能分布在2.65×10-9~2.98×10-9J,总体来说,各个纤维之间的转动动能差异较小。
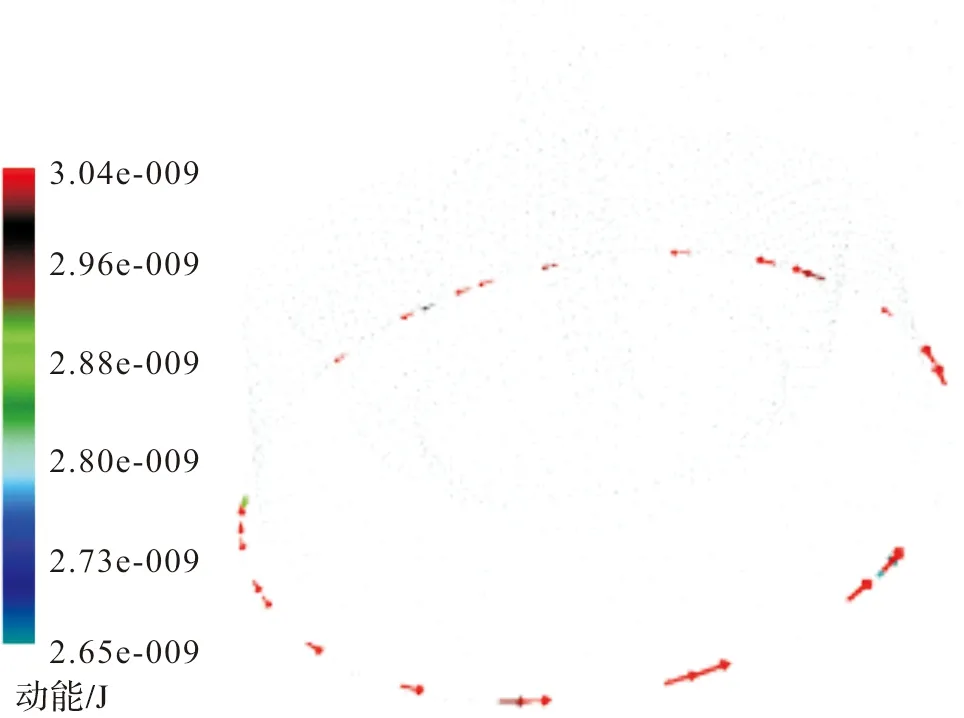
图13 纤维转动动能矢量图
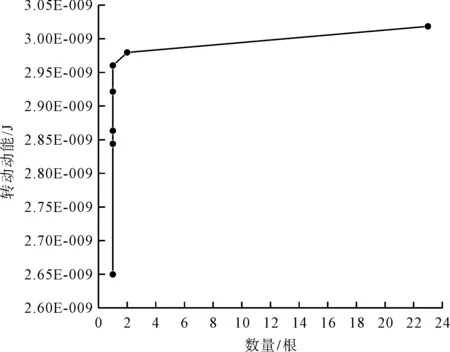
图14 纤维转动动能-数量分布
如图15所示,纤维的总受力为1.17×10-3~1.22×10-3N,纤维间的受力不匀是由于转杯内气流场的速度、压强分布不匀引起的。如图16所示,纤维的总受力方向指向转杯轴向,这样的受力分布有利于纤维在转杯底部的转移与剥离,是成纱的必要条件。如图17所示,纤维间的受力并不均匀,导致纤维受力不匀的原因是转杯内气流场的复杂性及纤维在转杯内受到较多力的作用;同时纤维从输纤通道进入转杯的时间及纤维在转杯底部的位置也不相同,也会使得纤维在受力上出现差异。纤维间受力不匀也反映出高速旋转的转杯内纤维凝聚成纱机理的复杂性。

图15 纤维在转杯内的受力
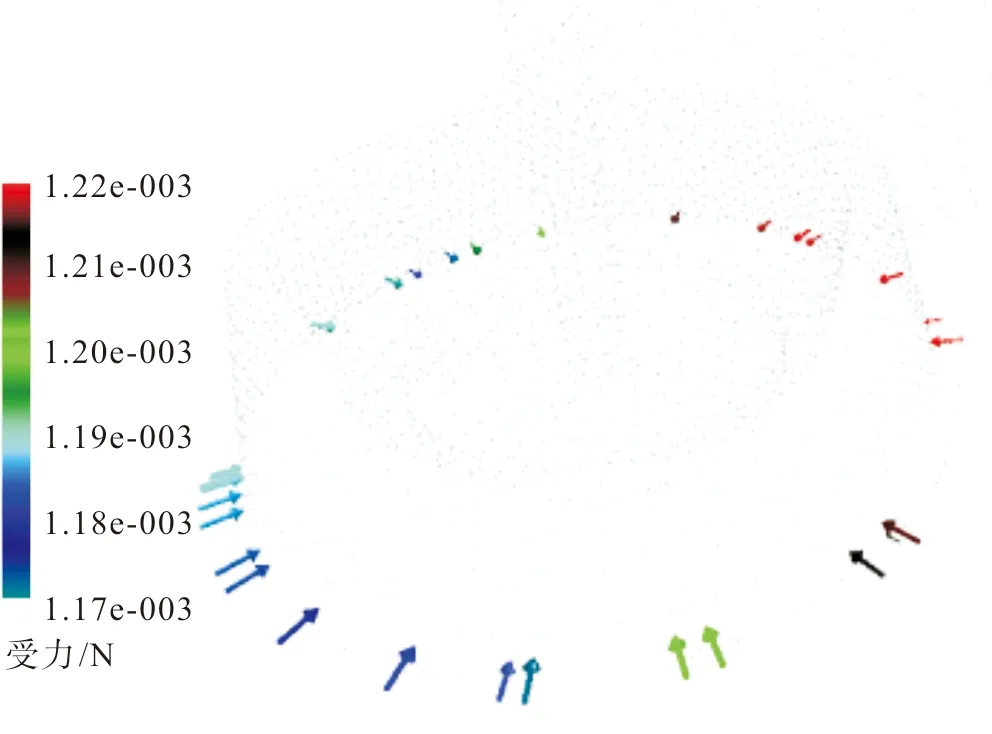
图16 纤维在转杯内受力矢量分布

图17 纤维总受力-数量分布
从图18可知,转杯内纤维的总能量分布在9.67×10-6~1.05×10-5J。在输纤通道出口与转杯滑移面交接处附近的纤维能量较低,为9.67×10-6~9.84×10-6J,如圆圈处所示。这是由于纤维从呈渐缩状的输纤通道出去后与转杯滑移面碰撞引起的,由动能公式E=1/2mv2知,动能与速度的平方成正比,碰撞使得纤维在此处的速度减小(图9),进而导致纤维的能量减小。为防止纤维在此处发生堆积,在转杯纺纱部件的设计中要合理选用转杯滑移面的滑移角度和输纤通道的倾斜角度,保证纺纱过程的顺利进行。

图18 转杯内纤维的能量分布
2.4 16 mm纤维在输纤通道内的运动分析
为了使纤维的物理模型更接近实际情况,本文进一步地观察纤维在输纤通道中的运动,现增加纤维长度至16 mm,EDEM中共计产生30根纤维,探究纤维在输纤通道中的运动。
图19展示了在时间t=0.000 1~0.001 5 s内纤维在输纤通道的运动状态。对各时段纤维的速度进行实时取值,并计算30根的平均值,分布如表2所示。1 mm和16 mm纤维的速度分布特征如图20所示。图19(a)中纤维束的前端形态较为发散,后端较为集中,是由于输纤通道中具有压强梯度和速度梯度,且越靠近输纤通道出口梯度变化越大,纤维两端产生压强差和速度差,使得纤维束头尾两端形态不同,进一步伸直平行。图19(b)中纤维紧贴着输纤通道下壁面运动,纤维速度分布在11.5~22.5 m/s,纤维速度间的差异反映了输纤通道中气流运动的复杂性。图19(c)中纤维有向输纤通道中心线运动的趋势,这与外国学者Kong等[12]的研究结论相一致,纤维的形态较为分散,是由于越靠近输纤通道出口气流对纤维的影响越大,使得纤维间的速度不同。图19(d)纤维速度整体进一步提高,纤维头端达到纤维输送通道出口处。图19(e)纤维速度在提高的同时,纤维头端由通道出口处向纤维壁面冲去。图20(f)中纤维头端与转杯滑移面接触并滑向转杯底部的凝聚槽内。图19(e)~(f)的中间过程中,由于纤维速度很快,从转杯滑移面到凝聚槽内会出现纤维堆积,为防止在输纤通道出口与转杯滑移面堆积过多纤维,输纤通道出口与转杯滑移面的距离要合适,避免纤维堵塞输纤通道出口。从图20可知,短纤维在各个时刻的速度及其平均值都要高于长纤维,有利于提高成纱速度,与生产中转杯纺对短纤维适应性强容易成纱的特点相符,但其在输纤通道与转杯壁面间受冲击气流影响较大,纤维速度急剧变化,部分纤维速度骤降,导致其累积在转杯壁面不能持续向前进入凝聚槽。这与实际生产中灰尘容易累在积转杯壁面的情况一致,灰尘颗粒细小,其速度特征可参考1 mm纤维。该模拟结果为进一步优化设计输纤通道与转杯壁面间的空间几何位置,弱化冲击波气流,减少细小尘杂颗粒与纤维的速度,提供了理论基础。如图21所示,输纤通道中t=0.000 1~0.001 5 s时刻气流和纤维的速度分布规律,输纤通道中气流的速度始终大于纤维的速度,有利于纤维的伸展,从而提高成纱质量。

图19 纤维在输纤通道中不同时刻的运动
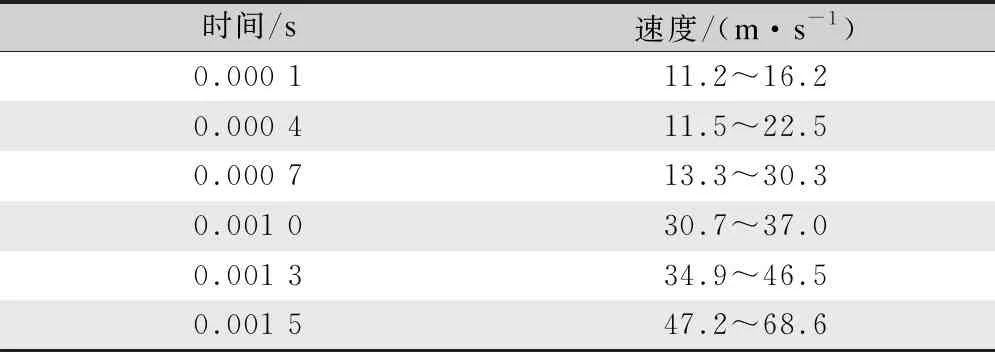
表2 16 mm纤维在不同时刻的速度分布
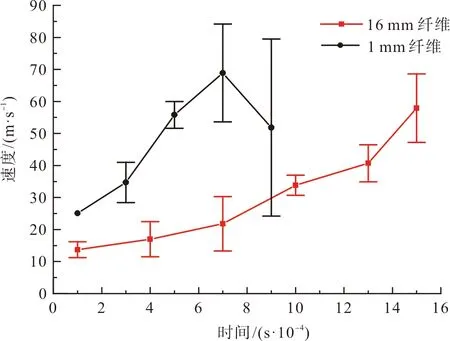
图20 不同长度纤维的速度分布特征
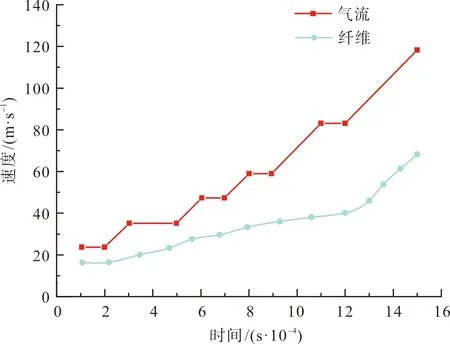
图21 输纤通道中不同时刻纤维与气流的速度
3 结 论
选用标准k-ε湍流模型和Hertz-Mindlin(No Slip)模型,通过Fluent 19.0与EDEM 2018耦合模拟了纤维在转杯纺纱通道内的运动状况,分析了纤维在转杯内的运动特征,得出了以下结论。
1) 纤维在输纤通道中做加速运动,1 mm纤维在纤维输送通道入口为25.1 m/s,到达凝聚槽内时84.2 m/s;16 mm纤维在纤维输送通道入口为11.2 m/s,到达凝聚槽内时68.6 m/s。
2) 纤维的速度与角速度之间相关性低,各个纤维之间的转动动能差异相对较小,纤维间速度与受力有差异,与转杯内复杂的气流场相关,反映出高速旋转的转杯内纤维凝聚成纱的复杂性。
3) 长纤维比短纤维总体速度偏低,不利于及时向转杯凝聚槽中输送纤维,容易在转杯滑移面处发生堆积,不利于成纱过程的顺利进行,因此转杯纺更适应短纤维成纱。
4) 输纤通道中的气流存在压强梯度和速度梯度,纤维在输纤通道中做加速运动,且在同一时刻输纤通道中气流的速度始终大于纤维的速度,这有利于纤维的伸直和输送,提高转杯成纱质量。

《丝绸》官网下载

中国知网下载

