基于整车操纵稳定性的横向稳定杆匹配设计

王浩

安徽江淮汽车集团股份有限公司 技术中心，安徽 合肥 230601

0 引言

汽车的操纵稳定性是指行驶过程中遇到来自路面不平及侧向风等外界干扰时，汽车能够抵抗干扰保持直线行驶的能力，是汽车安全行驶的重要基础。操纵稳定性好的汽车能够提高驾驶员的驾驶信心和驾驶乐趣。汽车的悬架刚度较小，可提高乘坐舒适性，但会导致悬架的侧倾角刚度偏小，侧向加速转弯时，较小的侧倾角刚度产生较大的侧倾角[1]，引起汽车过多转向趋势，对车身稳定性不利，驾驶员和乘客产生不安全的感觉。在悬架上安装横向稳定杆可有效解决这一问题，在不增加悬架垂直刚度的前提下，横向稳定杆提高汽车侧倾时的侧倾角刚度[2]，减小车身侧倾角，保证汽车的不足转向特性。

研究人员分析横向稳定杆对汽车操纵稳定性的影响。刘敬忠等[3]研究了某轻型客车前悬架扭杆和横向稳定杆角刚度对车辆转向灵敏度的影响；李志魁等[4]研究发现稳定杆安装衬套的径向刚度对稳定杆侧倾角刚度的影响较明显；刘一夫等[5]通过ADAMS/Car建立某微型轿车的刚柔耦合虚拟样车模型，仿真分析后发现横向稳定杆的结构参数和安装位置对悬架侧倾角刚度影响较大；梁毅等[6]、姜军平等[7]对比分析了横向稳定杆的安装位置对整车操纵稳定性的影响。

横向稳定杆的直径影响悬架的侧倾角刚度，基于整车操纵稳定性对前、后横向稳定杆直径匹配的研究较少，本文基于企业开发需求，在样车开发初期，采用ADAMS/Car软件建立样车仿真模型，对比不同前、后横向稳定杆直径组合方案对汽车操纵稳定性的影响，对最佳匹配方案搭载样车进行稳态回转试验，验证方案的合理性。仿真分析可在短期内对比验证不同方案，缩短样车设计所需的开发周期。

1 理论基础

悬架的侧倾角刚度对车身侧倾角有明显影响[8]，在悬架上安装横向稳定杆可有效解决侧倾角刚度足够大、偏频较低的问题[9]，能同时满足汽车操纵稳定性与舒适性的要求。麦弗逊悬架质量轻，响应速度快，是目前应用较广泛的悬架之一，本文以麦弗逊悬架为例计算悬架侧倾角刚度，示意图如图1所示。

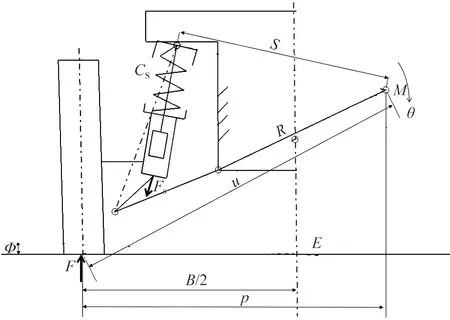
图1 悬架刚度计算示意图

假设弹簧的质量固定，悬架上下跳动时，可认为悬架不动而地面在运动，地面绕汽车中心线与地面的交点E转动角度Φ，Fs为弹簧施加的力，Cs为弹簧刚度，M为车轮的瞬时转动中心，假定转向节绕一侧车轮的瞬时转动中心转动角位移θ，F为地面对轮胎的法向反作用力，R为侧倾中心，p为轮胎中心线到瞬时转动中心的水平距离，B为轮距，S为减振器上安装点到瞬时转动中心的距离，u为轮胎接地点到瞬时转动中心的距离。

悬架的侧倾角刚度由弹簧垂直刚度和横向稳定杆侧倾角刚度2部分组成[10]。弹簧垂直刚度引起的悬架侧倾角刚度[11]

(1)

为简化计算，一般将横向稳定杆等效为等臂梯形，常用的麦弗逊前悬架横向稳定杆如图2所示。横向稳定杆引起的侧倾角刚度[12]

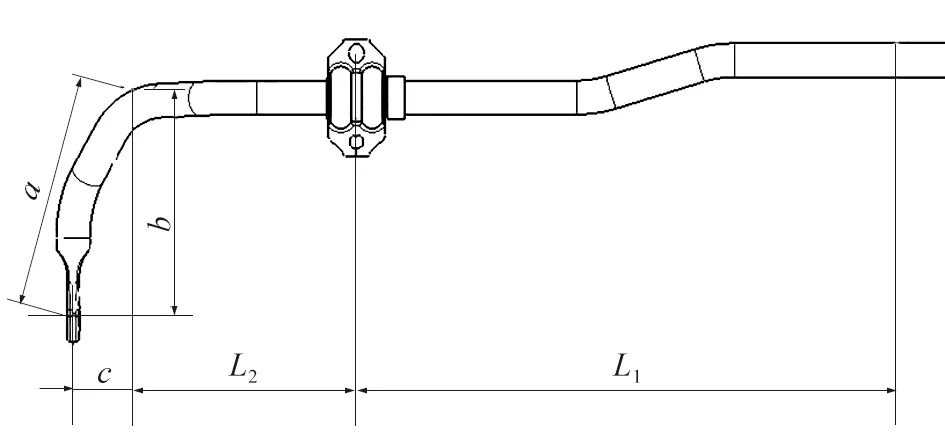
图2 麦弗逊前悬架横向稳定杆示意图

式中：E为横向稳定杆材料的弹性模量，E=206 kN/mm2；I为横向稳定杆截面惯性矩；L为横向稳定杆中点到拐点距离，L=L1+L2，其中L1为横向稳定杆中点到安装点距离，L1=290.43 mm，L2为横向稳定杆安装点到拐点距离，L2=166.85 mm；a为拐点到稳定杆和拉杆安装点距离，a=381.32 mm；b为拐点到稳定杆和拉杆安装点垂直距离，b=339.02 mm；c为拐点到稳定杆和拉杆安装点水平距离，c=74.84 mm。

悬架连接处衬套变形使悬架侧倾角刚度降低约15%～30%[13-14]，根据式(1)(2)的计算结果减去衬套变形影响的侧倾角刚度即为悬架实际侧倾角刚度。

2 车辆动力学仿真模型

2.1 悬架(含横向稳定杆)模型

样车的前悬架为麦弗逊独立悬架，后悬架为四连杆非独立悬架，根据整车架构尺寸、各零部件硬点、弹性元件设计参数搭建模型。

轮胎在路面不平和转向行驶中产生的拉伸、扭转、弯曲等复杂的力和力矩通过横向稳定杆和副车架传递给车身，因此需考虑副车架的应力变形情况，将其设定为柔性体[15-16]。采用ADAMS/Car软件建立刚柔耦合悬架模型，对前、后副车架进行模态分析计算，计算频率为200 Hz以下，以.MNF模态中性文件导入ADAMS/Car中，采用非线性梁单元格式建模，将横向稳定杆布置为对称式。实测悬架上各衬套的线刚度及扭转刚度如表1所示，其中x、y、z分别为纵向、侧向和垂向3个方向。

表1 悬架上各衬套的线刚度及扭转刚度

2.2 轮胎模型

汽车的轮胎是承受外界复杂激励、传递行驶驱动力的重要组成部分，轮胎对行驶平顺性和操纵稳定性起决定作用，因此需要结合车轮的六向力学特性和物理尺寸，建立能反映实际垂向刚度、侧向刚度、纵向刚度、扭转刚度、回正力矩等性能的动力学轮胎模型，否则将影响仿真分析结果，不能准确反映汽车的实际操纵稳定性[17]。综合考虑以上因素，建立PAC2002(PAC以魔术公式主要提出者Pacejka教授命名)轮胎模型，具体轮胎参数如表2所示。

表2 轮胎参数

2.3 转向系统模型

转向系统主要由方向盘、中间传动轴、输入轴、转向器、助力电机等结构组成。反映车轮转角和方向盘转角的转向系角传动比是动力学建模的重要输入参数，直接决定了操纵性响应的快慢。转向系角传动比iωo是驾驶员操作方向盘转过的角度和汽车转向轮的转角之比[18]，计算公式为：

式中：iω为转向器角传动比，iω′为转向传动装置角传动比，α为转向轮内轮转角，β为转向轮外轮转角，n为方向盘总圈数。

2.4 车身模型

若不考虑侧向风，可近似忽略车身形状对所建动力学模型分析结果的影响，即认为车身是只有质量没有大小的刚性体，车身的质心和转动惯量可通过K & C试验或参考车型近似估计，估算公式为：

Iz=mfr，

式中：Iz为绕z轴的转动惯量，m为整车质量，f、r分别为质心在水平方向距离前、后轮轮心的距离。

将车身近似为等效位置上的刚性体，建模时可通过质量球单元代替计算。

基于以上子模型建立车辆动力学仿真模型如图3所示。

图3 车辆动力学仿真模型

3 稳态回转试验

横向稳定杆对操纵稳定性的影响主要体现在对前、后轴侧偏角和车身侧倾角的影响，一般通过稳态回转试验进行分析。稳态回转试验是在车辆上安装陀螺仪和全球定位系统(global positioning system，GPS)等设备，测试并记录车辆侧向、纵向和横摆方向的速度，通过速度和时间计算加速度的变化曲线。一般规定在满载状态下，汽车先绕半径一定的圆周匀速行驶，固定方向盘角度后，以低于0.25 m/s2的加速度缓慢加速行驶[19-20]，此时侧向加速度ay和圆周半径均不断增大，为得到线性段和非线性段2个工况的数据，ay=6.5 m/s2时停止测试。通过测试得到的ay曲线，可计算前、后轴侧偏角之差与ay的关系。

初始转弯半径R0=15 m，第i时刻转弯半径

Ri=vi/ωri,i=1,2,…,t，

式中：vi为第i时刻的车速，m/s；ωri为第i时刻的横摆角速度，rad/s；t为测量时间。

汽车稳态回转时，前、后轴侧偏角之差

式中：L′为汽车轴距，L′=2.7 m；δ1、δ2分别为前、后轴侧偏角。

根据计算结果可绘制(δ1-δ2)-ay曲线。

3.1 仿真结果

分别分析横向稳定杆在车辆稳态回转线性范围(ay<0.4g，g为重力加速度)和非线性范围(ay=0.5g～0.6g)对车身侧倾角φ的影响。为获取所需结果，对仿真结果做如下处理：在(δ1-δ2)-ay曲线上取横坐标为0.20g(即ay=0.20g)处的曲线斜率为线性段不足转向度梯度U，取横坐标为0.55g(即ay=0.55g)处的曲线斜率为非线性段不足转向度梯度U′；在φ-ay的曲线上取横坐标为0.20g(即ay=0.20g)处的曲线斜率为车身侧倾梯度Kφ。

以样车初始布置的前稳定杆直径df=22 mm、后稳定杆直径dr=20 mm为基础，计算df分别为21、22、23、24、25、26 mm，dr分别为18、19、20、21、22、23 mm的不同匹配方案下Kφ、U、U′及前、后悬架的侧倾角刚度比，结果如表3、4所示。

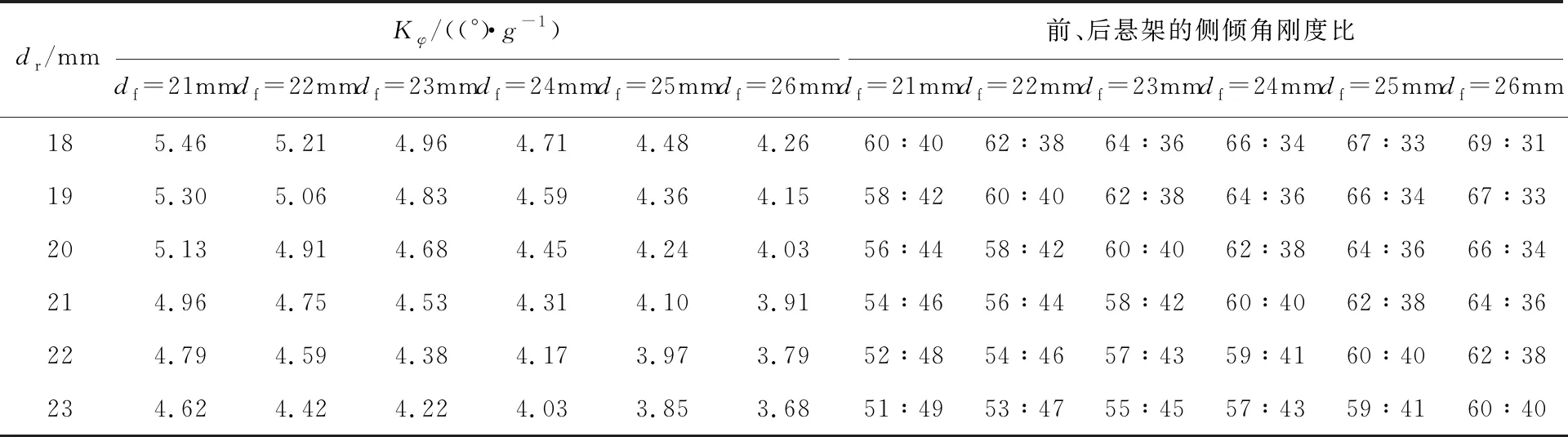
表3 ay=0.20g时的Kφ及前、后悬架的侧倾角刚度比

表4 ay=0.20g时的U及ay=0.55g时的U′ (°)/g

表4(续)

汽车稳态行驶时，离心力作用在车身质心上，引起车身侧倾产生φ，φ的大小取决于簧上质量绕侧倾轴转动的势能，势能大小受质心高度和侧倾轴相对关系的影响。前轮转向汽车的φ越大，前、后轮绕主销转动的角度越大，越容易发生侧倾转向；φ越小，轴荷转移也会降低，车辆具有较好的过弯稳定性和安全感。但需要驾驶员感受车辆在转向过程中一定的侧倾角度变化作为反馈，获取车辆的轨迹变化和车身表现，因此kφ也不能太小，根据大量标杆竞品车试验结果，推荐kφ=4～4.5 (°)/g[21]。

车辆应当具有适当的不足转向特性，不足转向梯度过小容易发生激转和甩尾，车辆和驾驶员不安全，不足转向梯度过大导致转向迟钝，丧失驾驶乐趣。根据目前乘用车的发展趋势，设定U=30～35(°)/g，U′=60～70(°)/g。

转向时车辆具有一定的ay，此时前、后悬驾的内、外侧轮胎上的重量转移主要受悬架的侧倾角刚度影响，汽车的不足转向特性发生变化，特别是在具有较大ay的非线性段，前悬架的侧倾角刚度越大，在前轴内、外侧车轮的载荷转移越明显，有利于减小前轴侧偏刚度，增加前轴侧偏角，保证不足转向特性；后轴趋势则相反。为获得较好的驱动性能，驱动轴两侧的负荷差异不能过大。为保证汽车具有适当的不足转向特性，一般要求前悬架的侧倾刚度大于后悬架，前、后悬架的侧倾角刚度比一般建议为1.6～2.4。

综合考虑以上因素，最佳匹配方案为df=24 mm、dr=20 mm。

3.2 试验结果

为分析仿真结果的合理性，对搭载前、后稳定杆直径分别为24、20 mm的样车在试验场进行稳态回转试验，试验前保证车轮四轮定位满足设计状态[22]，车轮胎压为厂家推荐值，试验环境满足文献[23]的要求，试验路面为坡度小于2%的沥青路[24]，试验设备布置如图4所示。

图4 稳态回转试验设备

将试验测得的φ-ay曲线、(δ1-δ2)-ay曲线与仿真分析得到的曲线进行对比，如图5、6所示。

图5 φ-ay曲线 图6 (δ1-δ2)-ay曲线

由图5、6可知：仿真曲线与试验曲线的变化趋势均基本吻合，可证明仿真模型的准确性和可行性。由图6可知：不足转向梯度随ay增大而增大，表明该车具有适当不足转向特性。

U、U′及Kφ的试验结果与仿真结果对比如表5所示。由表5可知：仿真和试验结果基本一致，试验得到的Kφ大于仿真结果是未考虑样车车身侧倾引起的载荷再次转移，导致φ增大。

表5 U、U′及Kφ的试验结果与仿真结果对比 (°)/g

4 结语

为分析前、后横向稳定杆直径对整车操稳性能的影响，基于ADAMS/Car建立车辆动力学仿真模型，针对不同直径的前、后稳定杆匹配方案，仿真分析车身侧倾梯度和线性段、非线性段的不足转向梯度随侧向加速度的变化，确定前、后横向稳定杆直径的最佳匹配方案，并搭载到样车上进行稳态回转试验，验证了仿真结果的准确性及匹配方案的合理性，达到在样车设计阶段快速匹配前、后横向稳定杆直径的目的。但本文中车身侧倾梯度及不足转向梯度均取自某一条固定侧向加速度的曲线斜率，未能完全反映车身侧倾角及前、后轴侧偏角之差的非线性变化情况。